1. Introduction
As the complexity of a system increases, its reliability decreases unless compensatory measures are taken. System reliability can be increased by increasing the reliability of its associated components, but sometimes this cannot be achieved beyond certain limits. An alternative way to increase the reliability in such situation is to have redundant configuration of components in the system.
Cascade system is one such special type of standby system. Cascade redundancy is a hierarchical standby redundancy, where an array of components (finite in number) are arranged in the order of activation. Here, the first component is active and the remaining components are at standby. The brunt of attack, in the first instance is borne by the active component. If it survives the attack, the system also survives with no loss and is ready to face the next attack. However, if the active component fails then the next component in the array has to face and withstand the “cushioned” attack on it. The stress acting on the subsequent active component will be “k” times the stress of the previous failed components, where “k” denotes stress attenuation factor.
Research works on reliability modelling and assessment related to cascade model as studied in the literature are quite exhaustive, Pandit and Sriwastav (1975) have featured relevance of geometric distribution in the study of behavior of a cascade system [1] . Raghavachar, Rao and Ramacharyulu (1983) presented a closed form solution of stress attenuated reliability function for n-cascade system when both stress and strength follow identical distributions [2] . Maheshwari, Rekha, Rao and Raghavachar (1993) studied stress attenuated reliability for n-cascade system whose stress and strength follow normal and exponential distributions respectively [3] . Rekha and Shyam Sunder (1997) have also highlighted a similar cascade system where stress and strength follow gamma and exponential distributions respectively. They showed that for higher parametric values and lower attenuation factors a high degree of reliability could be attained [4] . Rekha and ChechuRaju (1999) endeavored to present a closed form solution of stress attenuated reliability function for n-cascade system with exponential stress and standby strengths following Rayleigh and exponential distributions [5] . Shyam Sunder (2012) has studied stress attenuation for cascade system when both stress and strength follow Rayleigh distribution [6] . In most of the works mentioned in the literature on cascade model, study is carried out by considering the influence of stress attenuation factor only. This observation has motivated the present study of attempting to design reliability model for a cascade system under joint effect of stress as well as strength attenuation factors. Further, reliability assessment (estimation of reliability function) is carried using the standard methods [7] - [10] .
2. Estimation of Reliability for a (1 + 1) Cascade Model
2.1. Stress-Strength Cascade Model
Let 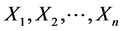 denote the strengths of n-components in the order of activation and let
denote the strengths of n-components in the order of activation and let 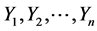 be the corresponding stresses acting on them. In a n-cascade system after every failure the stress gets modified by a factor “k” (stress attenuation factor) such that
be the corresponding stresses acting on them. In a n-cascade system after every failure the stress gets modified by a factor “k” (stress attenuation factor) such that 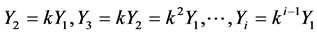 here,
here, 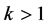 and we assume that the strength gets modified by a factor “m” (strength attenuation factor) such that
and we assume that the strength gets modified by a factor “m” (strength attenuation factor) such that 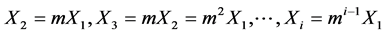 here,
here,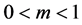 .
.
The reliability function 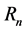 of the system with ‘n’ components is defined as,
of the system with ‘n’ components is defined as,
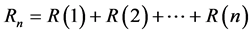
where,
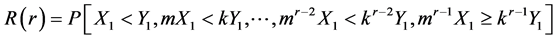 for
for 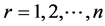
Cascade model with more number of standby components is not recommended as the strength goes on depleting with the order of standby which leads to dead investment. In view of this fact, we have considered estimation of reliability for a (1 + 1) cascade model.
2.2. Reliability Function for a (1 + 1) Cascade Model
To determine reliability function for the model under study, let us consider the strength of the two components (basic and standby) to be 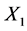 and
and 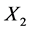 respectively, where
respectively, where 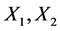 are independently and identically distributed (i.i.d) exponential random variables with parameter “
are independently and identically distributed (i.i.d) exponential random variables with parameter “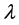 ”. Let
”. Let 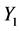 and
and 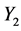 be the stress acting on the two components respectively, where
be the stress acting on the two components respectively, where 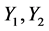 are i.i.d exponential random variables with parameter ‘
are i.i.d exponential random variables with parameter ‘ ’. To obtain the expression for reliability function, consider,
’. To obtain the expression for reliability function, consider,
![]() (1)
(1)
![]() (2)
(2)
Using results of (1) and (2), we obtain reliability function for the proposed (1 + 1) cascade model as,
![]() (3)
(3)
2.3. Life Testing Experiment
To obtain the estimators of “![]() ”, suppose “n” systems whose reliability function is defined as in expression (3) are put on life testing experiment. Here,
”, suppose “n” systems whose reliability function is defined as in expression (3) are put on life testing experiment. Here,
![]() are observed and
are observed and ![]() are i.i.d exponential random variables with parameters “
are i.i.d exponential random variables with parameters “![]() ” and “
” and “![]() ” respectively. Also, the data of stress
” respectively. Also, the data of stress ![]() are obtained separately from simulation of conditions of the operating environment and
are obtained separately from simulation of conditions of the operating environment and ![]() are i.i.d exponential random variables with parameter “
are i.i.d exponential random variables with parameter “![]() ” and “
” and “![]() ”
”
respectively. The joint probability density function of the random variables ![]() and
and ![]() is given by,
is given by,
![]() (4)
(4)
where,
![]()
The log-likelihood function of Equation (4) is obtained as,
![]() (5)
(5)
2.4. Estimators of Reliability Function (MLE & UMVUE)
Differentiating the log-likelihood function given in Equation (5) partially with respect to![]() ,
, ![]() and equating it to zero, we get,
and equating it to zero, we get,
![]() (6)
(6)
![]() (7)
(7)
Solving Equations ((6) and (7)) simultaneously, we get the Maximum Likelihood Estimator (MLE) of ![]() and
and ![]() as,
as,
![]() (8)
(8)
![]() (9)
(9)
Similarly, differentiating the log-likelihood function given in Equation (5) with respect to![]() ,
, ![]() and equating it to zero, we get,
and equating it to zero, we get,
![]() (10)
(10)
![]() (11)
(11)
Solving Equations ((10) and (11)) simultaneously, we get the MLE of ![]() and
and ![]() as,
as,
![]() (12)
(12)
![]() (13)
(13)
Using the invariance property of MLE, the MLE of reliability function ‘![]() ’ is obtained by substituting the MLEs of
’ is obtained by substituting the MLEs of ![]() in Equation (3) and is given by,
in Equation (3) and is given by,
![]() (14)
(14)
Here, ![]() denotes the estimator of reliability function obtained through MLE of the parameters. Further, estimator of the reliability function “
denotes the estimator of reliability function obtained through MLE of the parameters. Further, estimator of the reliability function “![]() ” attained through the Uniformly Minimum Variance Unbiased Estimator (UMVUE) of the parameters is obtained as follows.
” attained through the Uniformly Minimum Variance Unbiased Estimator (UMVUE) of the parameters is obtained as follows.
We know that, ![]() , implies
, implies ![]()
![]()
![]()
![]() (15)
(15)
Also, ![]() , implies
, implies ![]()
On similar grounds we have,
![]() (16)
(16)
Similarly, ![]() , implies
, implies ![]()
![]()
![]()
Substituting ![]() [result as mentioned in Equation (15)], we get,
[result as mentioned in Equation (15)], we get,
![]()
![]()
![]() (17)
(17)
Also, ![]() , implies
, implies ![]()
On similar grounds we have,
![]() (18)
(18)
Substituting the UMVUEs of ![]() in Equation (3), we get estimator of the reliability function “
in Equation (3), we get estimator of the reliability function “![]() ” obtained through the UMVUE of the parameters.
” obtained through the UMVUE of the parameters.
2.5. Asymptotic Distribution
To obtain the asymptotic distribution of![]() , let us denote the Fisher Information Matrix of
, let us denote the Fisher Information Matrix of ![]() as
as![]() .
.
![]()
where,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Thus, we have the Fisher Information Matrix as,
![]()
From the asymptotic properties of MLE under regularity conditions and multivariate central limit theorem we have,
![]()
![]() is inverse of Fisher Information Matrix “
is inverse of Fisher Information Matrix “![]() ”
”
where,
![]()
3. Simulation Experiment
For the ![]() system, the random variables
system, the random variables ![]() (with respect to strength) and random variables
(with respect to strength) and random variables ![]() (with respect to stress) are generated independently as follows:
(with respect to stress) are generated independently as follows:
Step 1: Initialize ![]() for the 1st and 2nd component of the system. Uniform random numbers
for the 1st and 2nd component of the system. Uniform random numbers ![]() is generated from
is generated from![]() . Further, expo-
. Further, expo-
nential random variable ![]() is obtained for the 1st component of the
is obtained for the 1st component of the ![]() system. Another uniform random numbers
system. Another uniform random numbers ![]() is generated from
is generated from![]() . Further, exponential random variable
. Further, exponential random variable ![]() is obtained for the 2nd component of the
is obtained for the 2nd component of the ![]() system.
system.
Step 2: The whole procedure in Step 1 is repeated for ![]() number of systems and the statistics
number of systems and the statistics ![]() are obtained.
are obtained.
Step 3: Initialize ![]() for the 1st and 2nd component of the system. Uniform random numbers
for the 1st and 2nd component of the system. Uniform random numbers ![]() are generated from
are generated from![]() . Further, ex-
. Further, ex-
ponential random variable ![]() is obtained for the 1st component of the
is obtained for the 1st component of the ![]() system. Another uniform random numbers
system. Another uniform random numbers ![]() are generated from
are generated from![]() . Further, exponential random variable
. Further, exponential random variable ![]() is obtained for the 2nd component of the
is obtained for the 2nd component of the ![]() system.
system.
Step 4: The whole procedure in Step 3 is repeated for ![]() number of systems and the statistics
number of systems and the statistics ![]() are obtained.
are obtained.
Step 5: With the help of the statistics ![]() and
and ![]() the MLE of parameters
the MLE of parameters ![]() of the model are obtained. Using these MLEs in the expression of reliability function, the MLE of reliability function is obtained.
of the model are obtained. Using these MLEs in the expression of reliability function, the MLE of reliability function is obtained.
Step 6: With the help of the statistics ![]() and
and ![]() the UMVUE of parameters
the UMVUE of parameters ![]() are obtained. Using these UMVUEs in the expression of reliability function, estimator of the reliability function based on UMVUE of the parameters is obtained.
are obtained. Using these UMVUEs in the expression of reliability function, estimator of the reliability function based on UMVUE of the parameters is obtained.
Table 1 and Table 2 give the results of the above simulation experiment for different values of ![]() and n.
and n.
4. Conclusion
From the above results (as shown in Table 1 and Table 2), we observe that reliability of
the system improves for larger values of strength attenuation factor (m) and for lower values of stress attenuation factor (k). Here, we also observed the estimates of reliability improves for larger value of the sample size “n”. This indicates that reliability of a system can be enhanced by strengthening the inbuilt mechanism of the system, which ultimately withstands the effects of the external environment in which it operates.
Further, on comparing the efficiencies of MLE of reliability function with reliability estimator obtained using UMVUEs of the parameters, we observed reliability estimator obtained from the UMVUEs of the perform better than the MLE of reliability function in terms of Mean Square Error (MSE) for the given data set. This emphasizes the need to strengthen the processes such that they are least affected by effects of the variation factors which intern boost the reliability of the operating system.