Combinatorial Preon Model for Matter and Unification

Risto Raitio

Espoo, Finland.

DOI: 10.4236/oalib.1103032                

Abstract

I consider a preon model for quarks and leptons based on constituents defined by mass, spin and charge. The preons form a finite combinatorial system for the standard model fermions. The color and weak interaction gauge structures can be deduced from the preon bound states. By applying the area eigenvalues of loop quantum gravity to black hole preons, one gets a preon mass spectrum starting from zero. Gravitational baryon number non-conservation mechanism is obtained. Argument is given for unified field theory is based only on gravitational and electromagnetic interactions of preons.

Keywords

Preons, Standard Model, Quantum Black Hole, Statistical Mechanics, General Relativity, Loop Quantum Gravity

1. Introduction

The purpose of this note is to reinforce a draft model for particles, their interactions and spacetime [1] - [3] . The difficulty of constructing a unified picture of “everything” is realized. It has been questioned whether such popular elements, like grand unified theories (GUT) of gauge interactions, supersymmetry or, most intriguingly, superstring theory, do occur in nature. It would be mathematically satisfying to use current methods and start from the quantum and entanglement and proceed to spacetime, see e.g. [4] - [8] . However, some of these elements lack experimental support, and some issues of theoretical nature remain unresolved. The history of quantum gravity perhaps indicates the need for a different approach¹.

The phenomenological approach taken here is to divide the unification problem into mutually consistent component models. A new proposal is made in this note for the key component, the preon model. It provides a method for deducing the standard model (SM) properties and for a novel unification of interactions and of matter and spacetime. Preons can be understood on one hand as lowest level, freely combining constituents, see Section 2, or on the other hand, quantum black hole dynamical objects, see Section 5. Except for the interactions between the preons, the different component models are supported by calculations and can be logically glued together to form a reasonable unity but more general theoretical principles remain to be discovered.

The present analysis is based on the phenomenological success of the SM of particles up to LHC energies and, the somewhat doubted, stability supposedly up to Planck energies [11] . When coming to Planck scale energies there are no data available and we have to turn heavily to Gedanken experiments. I end up tentatively preferring preons emerging from spacetime being primary and suitable for creating the universe in con- secutive steps with few assumptions.

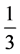I reanalyze a model of quarks and leptons proposed in [1] . The basic idea is to construct the quarks and leptons out of two preons which have spin, charge or

0 and some light mass. The preons form a three member combinatorial system for the SM fermions. Furthermore, from this basis also the color and weak interactions of particles can be deduced. Unification of interactions is proposed on preon level with gravity and electromagnetism only.

Originally the preons were peculiarly assumed to be micro black holes (BH) with Planck scale mass leading to the serious problem of getting light quarks and leptons from them. New developments in quantum gravity studies have come to help [12] - [14] . The mass spectrum of BH preons is found to start from zero using the area eigenvalues of loop quantum gravity (LQG). The model predicts a mechanism the gravitational decay of the proton. This decay is due to an explicit preon interaction instead of a general black hole quantum number erasure process. The quantization of micro BHs is done based on the BH horizon model proposed in [15] . The model is a statistical mechanical construction based on area quantization of LQG.

This paper is organized as follows. In Section 2 the main subject of this note, the preon model, is discussed. The fermion generations and non-Abelian interactions of the SM are discussed in Section 3. Kaluza-Klein theories as candidate theory for interaction unification are briefly reviewed in Section 4. LQG area eigenvalues are applied to the preon model in Section 5 to build matter-spacetime unification. Sections 3 - 5 contain review material relevant to the present model. Finally in Section 6 I give a brief summary of the results and conclusions. Being a scheme proposal the presentation is very concise throughout.

2. The Preon Model

2.1. Preon Combinatorics Form Quarks and Leptons

To build a model for unified picture of matter and spacetime implies some internal structure for quarks and leptons at scale of the order of Planck length. Such a model has been proposed in [1] . The basic idea there is that the quarks and lepton are made of preons, or maxons, characterized by three quantum numbers: mass, spin and charge. Their values are: mass provisionally the Planck mass (but later dynamically

zero), spin 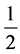and charge 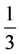or 0. In addition there is “color” (i, j, k) as a permuta- tion index for identical fermions.

Requiring charge quantization {0, 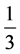, , 1}, with physical particles having an integer charge and preon permutation antisymmetry for identical preons, one can define creation operators to pull out of vacuum these states:

(1) one preon makes nothing observable, it must combine with others,

(2.a) two preons may form a charged boson (), which can combine with a preon 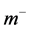(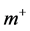) to form a 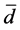(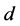) quark or with a preon () to form a positron (electron), the charged boson may also be a 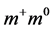(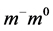) state which may combine with an () to form a () quark or with an to form a () quark,

(2.b) two preons may form a neutral boson of spin 0 or 1,

(3) three preons may form the first generation quarks and leptons which are the following bound states

(2.1)

The preons combine freely without extra assumptions into standard model fermion bound states. They form a three member combinatorial system. I assume that these states are bound by gravitational or scalar (or other Planck scale) force the details of which are not important to low energy physics. Properties of this interaction, together with the number of scalar and vector preon-antipreon bosons, should be studied separately as a future project. The Coulomb repulsion problem between like-charged preons in (2.1) is discussed later in this section.

A useful feature in (2.1) with two identical preons is that the construction provides a three-valued index for quark SU(3) color, as it was originally discovered [16] . In addition, the weak SU(2) left handed doublets can be read from the first two and last two lines in (2.1). The SM structure can be deduced in this sense from the present preon model².

One may now propose that, as far as there is an ultimate unified theory, it is a preon theory with gravitational and electromagnetic interactions only. The strong and weak forces are generated later when quarks and leptons are formed at lower temperature in the early universe and they operate only with short interaction range within nuclei making atoms and molecules possible.

Spin quarks and leptons are implied by this model. States with higher number of preons are possible but will not be considered here.

The proton, neutron, electron and can be constructed of 12 preons and 12 anti-preons as seen in Table 1. The particles in the right hand column are the basic - decay particles.

2.2. Preon Mass Scale

We will see in Section 5 that BHs may undergo a phase transition at a certain, so that above BH masses are above Planck scale, , and spacetime approaches classical spacetime. But below zero preon mass is possible. This comes about in LQG as follows. Below the critical temperature the basic elements of LQG, the punctures or strands, coming out of the stretched horizon are in their lowest energy state, the vacuum, and there is no ordinary radiating black hole. Above the strands get excited, , and have the possibility of falling back into the vacuum by emitting Hawking radiation.

The critical temperature is defined by (5.10). In terms of the acceleration a caused by gravity on the stretched horizon. The value of a near the event horizon is where is the Schwarzschild radius of the BH. This diverges on the horizon and is therefore model dependent near the horizon. A reliable estimate of the order of magnitude of is obtained from the Planck temperature

where is the Boltzmann constant.

If the preon mass scale is the Planck scale (2.1) would be superheavy particles. To get the standard model particles the large mass reduction has to be explained. This is done in Section 5: in (5.1) setting leads by (5.2) to zero mass “cold” black hole. Around a cold preon the spacetime metric is Minkowski metric. The preon may interact with the Higgs field and gain a light mass.

Table 1. Preons, anti-preons and particles.

The mass scale change is significant. It may be understood, using non-relativistic quantum mechanics as a heuristic guide, by assuming that when the continuum spacetime geometry () changes to vacuum geometry () the preon falls inside a potential well of depth and acquires zero mass, see Section 5. When the temperature after Big Bang/Bounce cools down potential wells expand in space at with the preons starting to dominate. Primordial BHs would stay, or form, in regions with higher temperature (Section 5).

At this point also the generalized uncertainty principle (GUP), , should be discussed. This would need more consideration and is left for future task (beyond the general result). For a review of GUP questions, see e.g. [17] .

The construction (2.1) is matter-antimatter symmetric on preon level, which is desirable for early cosmology. The model makes it possible to create from vacuum a universe with only matter: combine e.g. six, six and their antiparticles to make the basic -decay particles, see Table 1. Corresponding antiparticles may occur equally well.

The baryon number (B) is not conserved [18] - [20] in this model: a proton may decay at Planck scale temperature by a preon rearrangement process into a positron and a pion, see Table 2. This is expected to be independent of the details of the preon interaction. Baryon number minus lepton number is conserved³.

The large mass reduction from Planck scale to zero would also imply shrinkage of the BH from three spatial dimensions to a point, which serves as the zero element of area addition (not necessarily meaning dropping out of spacetime).

For charged BHs the situation is one step more complicated because they have classically two horizons, the event horizon and an internal Cauchy horizon located where the component

(2.2)

of the Reissner-Nordström metric diverges. (2.2) has two solutions

(2.3)

The characteristic length scale of the internal horizon is (in SI units)

(2.4)

Table 2. Proton decay into a positron and pion by preon rearrangement.

For an electron like particle with charge this gives, i.e. about one hundreth of the Schwarzschild radius. The two concentric horizons become one for.

Before the quarks and leptons are formed at high temperature in the early universe the preons collide coming so close each other that charged preons may join to form a two or three preon “clusters” of fermions with a common surface charge distribution. We assume that the charge is distributed, as a first approximation, uniformly on the degenerate horizon of the charged preons. This way Coulomb repulsion problems between preons inside quarks and leptons are avoided.

Though the geometries for neutral and charged BHs are different we expect the mass reduction mechanism to zero mass work for both cases.

The standard model gauge bosons and the Higgs would be elementary (but their composite nature is not ruled out). The three generations would be due to a gravi- tational or scalar interaction or a new symmetry as in [22] [23] , see Section 3.

In the early universe at high temperature the standard model quarks and leptons would be formed only after all matter had been in the form of charged black holes and later preons. Quarks and leptons would appear when the temperature decreases enough. Therefore electroweak and QCD interactions come to play rather late.

Some fraction of primordial black holes should remain black making dark matter. Their masses are expected to be around. In [24] the authors discuss the pos- sibility that LIGO has detected dark matter in black hole mergers.

3. Framons, Generations and Unification

To account for the fermion generations, I refer to the review of Yang-Mills theory and the SM [22] , see also [23] . The authors want to understand first of all the origin of the Higgs mechanism and the generations of quarks and leptons. In the limited space of this note I mention that the authors introduce frame vectors in internal space as field variables, framons, in addition to the usual gauge theory boson and fermion variables. They obtain the standard Higgs scalar as the framon of the electroweak sector and a global color symmetry to provide the three fermion generations. Using renormalization of framon loops, which change the orientation in generation space of the vacuum, hence also the mass matrices of fermions and lets them rotate with changing energy scale. As a result they obtain tremendous fit to all data. The analysis leads automatically to CKM mixing and neutrino oscillations, hierarchical generation masses and the strong-CP problem.

The traditional gauge unification picture holds in the present scheme up to the unification energy of about 10¹⁶ GeV. The electroweak interaction has the spontane- ously broken symmetry phase at low energy but the electromagnetic and weak forces take separate ways at higher energies, the former melts away due to “ionization” of quarks and leptons into preons, but the latter stays strong towards Planck scale,. Likewise the quark color interaction suffers the same destiny as the weak force. One is left with the electromagnetic and gravitational forces only at Planck scale. The ultimate unification of forces may take place there. This has a long and diverse history, see Section 4. The weak and strong forces provide the means for shorter scale structures in nuclei and operate also in stars. The gravitational and elec- tromagnetic interactions have long range and, especially the former, is truly cosmo- logical in nature.

A second feature in the unification scheme proposed here is the connection of preons to micro black holes, and therefore to spacetime. This is done assuming the preons being black hole like particles in the quantum geometry of loop gravity. It is shown in Section 5 that at low temperature the preon mass spectrum starts at zero instead of. There is evidence that the singularity problem of BHs and the Big Bang/Bounce would also be solved.

4. Going into Fifth Dimension

This section includes a summary of some important historical milestones that should be useful in building unified models, though the results are not yet exactly what is required. I start with a very brief summary of the well known, but underrated Kaluza- Klein (KK) theory⁴ [25] [26] .

Nordström showed [27] in 1914 and Kaluza [28] in 1921 that five dimensional GR contains both Einstein’s four dimensional gravity and Maxwell’s electromagnetism. Klein [29] in 1926 suggested to compactify the fifth dimension. These models have further three interesting properties: (1) matter (radiation) in 4D is a manifestation of pure geometry in 5D, (2) the higher dimensional theory is a minimal extension of GR, and (3) physics does not depend on the fifth coordinate.

On classical level the KK metric is

(4.1)

where Latin indices run from 0 to 4 and Greek from 0 to 3. The Einstein-Maxwell action is

(4.2)

The fifth dimension integral dy is over a compactified angular variable with radius of the order of. This is a candidate for a unified classical gravitational and electro- magnetic theory of preons, including the graviton, photon and a scalar field, which is sometimes set as constant like 1.

In quantum theory each of these fields, say f(x,y), is often written in terms of Fourier expansions

(4.3)

In the y-direction these modes have a momentum of the order of, which for reaches the Planck scale. Therefore only modes with are observable.

Let us consider matter in the five dimensional theory, a massless scalar field in Minkowski space with action

(4.4)

where

(4.5)

The field can be written as Fourier sum as in (4.3) and inserted into the action (4.4)

(4.6)

One can read both the charge and mass of the scalar modes

(4.7)

Taking one gets

(4.8)

which is a reasonable value and illustrates the point of making the KK theory attractive with better agreement (the value of quantity could be determined more accu- rately).

The scalar mode masses behave rather badly. The electron mass would be. This problem can be avoided by three things. First, by identifying the light particles with. Thereafter the Higgs couplings are applied to make the masses in the observed region. But now the charge of the mode is zero. This is arranged by going to one more higher dimension where massless particles are no longer singlets of the gauge group corresponding to the ground state. Massless scalar field in the adjoint representation of the gauge group can be introduced as follows

(4.9)

which have in general non-zero couplings to the gauge fields.

The KK theory, with its promising features, cannot be considered fully understood at the moment. It has been extended up to 11 dimensional supergravity theory with a possibility for SU(3) × SU(2) × U(1) gauge group but with difficulties for proper fermion quantum numbers [30] . The point of this note is to propose one more structural level below quarks and leptons but fewer interactions, gravity and electro- magnetism only, and lower dimensions, tentatively five, at Planck scale.

5. Black Hole Phase Transition in Loop Quantum Geometry

A brief description is given below of black hole preon quantization using a statistical mechanical model where the areas, and therefore the energies, of the horizon are quantized and used to calculate the partition function. In LQG geometry the area eigen- values are [12]

(5.1)

where the sum is over punctures p of the spin network, is the Planck length, is the Barbero-Immirzi parameter and the values of are. The spin

number describes the size of the quanta of space [31] . For comprehensive treat- ments of quantum geometry and black holes see e.g. [32] [33] .

The energy of a black hole from the point of view of an observer on its stretched horizon is called Brown-York energy [34]

(5.2)

where a is the constant proper acceleration of an observer on the stretched horizon and A is the area of the horizon. In [35] quasilocal isolated horizons are considered which capture the main local features of horizons. The energy expression (5.2) remains the same.

For the BH spacetime model the partition function for a spin network with N punctures is, for details see [15]

(5.3)

where and, with The resulting is

(5.4)

where

(5.5)

When one has simply.

The average energy at temperature can be calculated from the partition function (5.3)

(5.6)

of the black hole which yields

(5.7)

In LQG it is assumed that the number of punctures on the stretched horizon is very large, say about 10¹²². Therefore for (5.7) simplifies to

(5.8)

For, approaches zero for large N and one gets

(5.9)

There is a jump in energy of the hole when. Since y depends on temperature according to (5.5) on sees that the hole undergoes a phase transition at the critical temperature defined by the solutions of

(5.10)

Below the critical temperature the punctures of the stretched horizon are in vacuum and there is no ordinary black hole. Above the punctures get excited and provide the possibility of falling back to vacuum with Hawking radiation being emitted simultaneously.

From and (obtained numerically) and choosing one gets

(5.11)

which is the Davies-Unruh temperature felt by an observer on the stretched horizon with constant acceleration a. The Hawking temperature can also be derived

(5.12)

6. Conclusions

There are at present a number competing candidate theories for quantum gravity like string theory, loop quantum gravity, causal dynamical triangulation, and others. The area eigenvalues of loop quantum gravity were used in Section 5 for model building. It is hoped that LQG, or some other such theory, will soon provide a consistent picture of quantum geometry in 4D and 5D for a unified theory.

The model of Sections 2 and 5 goes deep into the structure of the physical universe and can be considered a novel candidate for a unified scheme of “everything”, in the sense discussed here. In the scenario briefly outlined above, the composite quark and lepton model, the horizon properties of black holes and LQG area eigenvalues look promising ingredients on the road towards the origin of spacetime, quantum gravity and matter.

NOTES

¹Recently it has been shown that the relationship between spacetime geometry [9] and entanglement should exist, or have an analog, in quantum gravity with diffeomorphism invariance [10] in loop quantum gravity, of which we make use later in this note.

²It is trivial to get the charges between 0 and 1 but its is pleasing that the gauge groups can be deduced.

³Basically, I have followed the guide of [18] that “black holes should be subject to the same rules of quantum mechanics as ordinary elementary particles or composite systems”. The question what is a particle is discussed in [21] .

⁴I believe this is because of the developments in quantum mechanics about 1925 and later discovery of new particles shifted the interests of the majority of physicists away from it and from gravity. While quantum mechanics deserved its attention Einstein's later works, though considered failure, may not have had a fair evaluation.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Raitio, R. (1980) A Model of Lepton and Quark Structure. Physica Scripta, 22, 197. http://dx.doi.org/10.1088/0031-8949/22/3/002
[2]	Raitio, R. (2016) A Statistical Model of Spacetime, Black Holes and Matter. Open Access Library Journal, 3, e2487. http://dx.doi.org/10.4236/oalib.1102487
[3]	Raitio, R. (2016) Standard Model Matter Emerging from Spacetime Preons. Open Access Library Journal, 3, e2788.
[4]	Maldacena, J. (1998) The Large NN Limit of Superconformal Field Theories and Supergravity. Advances in Theoretical and Mathematical Physics, 2, 231-252. http://dx.doi.org/10.4310/ATMP.1998.v2.n2.a1
[5]	Van Raamsdonk, M. (2010) Building up Spacetime with Quantum Entanglement. International Journal of Modern Physics D, 19, 2429-2435. http://dx.doi.org/10.1142/S0218271810018529
[6]	Lashkari, N., McDermott, M. and Van Raamsdonk, M. (2014) Gravitational Dynamics from Entanglement “Thermodynamics”. JHEP, 1404, 195. http://dx.doi.org/10.1007/JHEP04(2014)195
[7]	Faulkner, T., Guica, M., Hartman, T., Myers, R. and Van Raamsdonk, M. (2014) Gravitation from Entanglement in Holographic CFTs. JHEP, 1403, 51.
[8]	Swingle, B. and Van Raamsdonk, M. (2014) Universality of Gravity from Entanglement.
[9]	Ryu, S. and Takayanagi, T (2006) Holographic Derivation of Entanglement Entropy from the Anti-De Sitter Space/Conformal Field Theory Correspondence. Physical Review Letter, 96, 181602. http://dx.doi.org/10.1103/PhysRevLett.96.181602
[10]	Smolin, L. (2016) Holographic Relations in Loop Quantum Gravity.
[11]	Tang, Y. (2013) Vacuum Stability in the Standard Model. Modern Physics Letters, A28, 1330002. http://dx.doi.org/10.1142/S0217732313300024
[12]	Rovelli, C. and Vidotto, F. (2015) Covariant Loop Quantum Gravity, Cambridge Monographs on Mathematical Physics.
[13]	Chiou, D.-W. (2015) Loop Quantum Gravity. International Journal of Modern Physics, D24, 1530005. http://dx.doi.org/10.1142/S0218271815300050
[14]	Rovelli, C. (2011) Zakopane Lectures on Loop Gravity.
[15]	Makela, J. (2016) Phase Transition in Loop Quantum Gravity. Physical Review D, 93, 084002.
[16]	Greenberg, O. (1964) The Color Charge Degree of Freedom in Particle Physics.
[17]	Tawfik, A. and Diab, A. (2015) A Review of the Generalized Uncertainty Principle. Reports on Progress in Physics, 78, Article ID: 126001. http://dx.doi.org/10.1088/0034-4885/78/12/126001
[18]	‘T Hooft, G. (1985) On the Quantum Structure of a Black Hole. Nuclear Physics B, 256, 727-745. http://dx.doi.org/10.1016/0550-3213(85)90418-3
[19]	Bekenstein, J. (1972) Non Existence of Baryon Number for Static Black Holes. Physical Review D, 5, 1239-1246. http://dx.doi.org/10.1103/PhysRevD.5.1239
[20]	Wheeler, J. (1971) Cortona Symposium on Weak Interactions. Edited by Radicati, L., Accademia Nazionale dei Lincei, Rome.
[21]	Rovelli, C. and Colosia, D. (2009) What Is a Particle? Classical and Quantum Gravity, 26, Article ID: 025002.
[22]	Chan, H.-M. and Tsou, S. (2015) The Framed Standard Model (I) and (II).
[23]	Chan, H.-M. and Tsou, S. (1998) Physical Consequences of Non-Abelian Duality in the Standard Model. Physical Review D, 57, 2507-2522. http://dx.doi.org/10.1103/PhysRevD.57.2507
[24]	Bird, S., Cholis, I., Munoz, J., Ali-Haimoud, Y., Kamionkowski, M., Kovetz, E., Raccanelli, A. and Riess, A. (2016) Did Ligo Detect Dark Matter?
[25]	Overduin, J. and Wesson, P. (1997) Kaluza-Klein Gravity. Physics Reports, 283, 303-380. http://dx.doi.org/10.1016/S0370-1573(96)00046-4
[26]	Duff, M. (1994) Kaluza-Klein Theory in Perspective. The Oskar Klein Centenary Nobel Symposium, Stockholm, 19-21 September 1994.
[27]	Nordstrom, G. (1914) über die moglichkeit, das elektromagnetische Feld und das Gravitationsfeld zu vereinigen. Physikalische Zeitschrift, 15, 504-506.
[28]	Kaluza, T. (1921) Zum unitstaetsproblem in der physic. Sitz. Preuss. Akad. Wiss. Phys. Math., K1, 966.
[29]	Klein, O. (1926) Quantentheorie und funfdimensionale Relativittstheorie. Zeitschrift fur Physik A, 37, 895-906.
[30]	Witten, E. (1981) Search for a Realistic Kaluza-Klein Theory. Nuclear Physics B, 186, 412-428. http://dx.doi.org/10.1016/0550-3213(81)90021-3
[31]	Ariwahjoedi, S., Astuti, V., Kosasih, J., Rovelli, C. and Zen, F. (2016) Statistical Discrete Geometry.
[32]	Ashtekar, A., Baez, J., Corichi, A. and Krasnov, K. (1998) Quantum Geometry and Black Hole Entropy. Physical Review Letters, 80, 904-907. http://dx.doi.org/10.1103/PhysRevLett.80.904
[33]	Barbero, G.J. and Perez, A. (2015) Quantum Geometry and Black Holes.
[34]	Brown, J. and York Jr., J. (1993) Quasilocal Energy and Conserved Charges Derived from the Gravitational Action. Physical Review D, 47, 1407-1419. http://dx.doi.org/10.1103/PhysRevD.47.1407
[35]	Frodden, E., Ghosh, A. and Perez, A. (2013) Quasilocal First Law for Black Hole Thermodynamics. Physical Review D, 87, Article ID: 121503. http://dx.doi.org/10.1103/PhysRevD.87.121503