The Contribution of the Gravitational Propagation Delay to Orbital and Center of Mass Motions ()
1. Introduction
The small effect of the propagation delay of the gravitational interaction on the motion of the Earth Moon and the Brown Dwarf 569Bab binary star system is analyzed. The calculated values are in very good agreement with observed values.
Recent measurements have shown that gravitational waves and thus the gravitational interactions propagate with the speed of light. This is described by B. P. Abbott et al. [1] in an article in Physical Review Letters.
The gravitational propagation delay exists whether the interaction is modeled by the deformation of the four dimensional space due to the mass of the bodies, or it is modeled by a gravitational interaction that is propagating between objects. In each case a change in position of one object takes time to be sensed by the other object.
Neither Newtonian Classical Mechanics nor the General Theory of Relativity considers delayed interactions [2] [3] .
The systems considered here are neither extremely massive, by astronomical standards, nor do they move with velocities that are a substantial portion of the speed of light. For such systems the Kepler-Newtonian Mechanics [2] gives fairly accurate results. This calculation is for small changes in the various parameters of the Kepler orbits. The calculation performed here is only valid for a gravitational propagation delay time that is much smaller than the orbital period.
The finite propagation delay of the gravitational interaction couples the orbital and center of mass motions. The main effect of the delay in the gravitational interaction is that the orbits grow very slowly. The loss in orbital energy is transferred to the center of mass motion. This causes the center of mass to accelerate. The acceleration is not linear since part of the orbital angular momentum is transferred to the center of mass motion.
In galaxies, too, the average propagation time of the gravitational interaction between the star cloud and central black hole is much smaller than the orbital period of the star cloud. Thus, the effect of the gravitational propagation delay on galaxies should also exhibit a growth of the distributed star cloud and an acceleration of the center of mass.
One can consider the very large number of star systems, galaxies, and galactic clusters as molecules of the universe. The transfer of internal orbital energy to the molecular motion will cause the universe gas to heat and expand. Alternatively, one should include the loss in orbital internal energy of the galaxies and other orbiting objects in the mass and energy of the universe when considering its accelerating expansion [4] . Conventionally Magic Dark Matter has been used to explain the accelerating expansion of the Universe [5] .
After completing its final run, scientists at the extremely sensitive Large Underground Xenon (LUX)?Zeplin [6] experiment announced they have found no trace of Magic Dark Matter particles. Dark Matter is postulated to be carried by Weakly Interactive Massive Particles (WIMP) s. Measurements with the very Large Hadron Collider at CERN has verified with increasing accuracy the so called Standard Model of sub atomic physics. But it has failed to detect any particle, such as Neutralino, associated with Magic Dark Mass. Thus, all attempts to measure Dark Mass or Dark Energy [6] [7] [8] have failed to produce any evidence of their existence to date.
Perhaps Dark Mass is like the Ether of the end of the 19th century through which electromagnetic waves were supposed to propagate. The Michelson Morley experiment showed in 1887 that the aluminiferous Ether does not exist. These experiments were repeated with greater and greater accuracy until 1920 without detecting an aluminiferous Ether. In 1905 Einstein showed that the aluminiferous Ether was not necessary for electromagnetic wave propagation.
There are a number of small corrections to the Kepler Newton model:
For the Earth Moon system there are interactions with the sun and the other planets. This effect mainly results in a small change of the orbit and in the Apsidal precessions of the orbits [9] .
There is an increase in the orbits explained by tidal effect [10] [11] due to flexing of the interacting bodies. The periodically flexing of the orbiting bodies due to tidal effects converts some of the orbital energy to heat.
There are small effects due to the curvature of space near masses explained by the General Relativity Theory [3] [12] . The General Relativistic model mainly provides a small correction to the precession of the orbits.
Here the small contribution to the orbital motion due to the finite propagation delay of the gravitational interaction is calculated. The calculated values are in very good agreement with observed values.
Another result is that the analytically describable spiraling out of the semimajor axis starts at a time that is much less than the age of the system. This probably can be caused by a collision of one of the system components that obscured the previous analytical describable motion. The time of the past collisions is calculated. The spiraling out of the Lunar orbit, analyzed here, starts in the Pliocene and Miocene epochs, long after the Dinosaurs have disappeared.
The gravitational interaction is an attractive force. In this case the force points in a direction opposed to the direction it travels. It can be demonstrated that the delayed gravitational interaction is completely causal as shown in Figure 1.
A force FRthat was radiated by the Earth in the past is received currently by the Moon. This is a Retarded force.
The Moon radiates a force FAcurrently that the Earth might or might not receive in the future. This is an advanced force.
By Newton’s law of action and reaction the Moon experiences a recoil force FRecoilequal in magnitude and opposed in direction to the force FAit radiated. The recoil force is independent whether or not the Earth receives the radiated force in the future. The forces are continually radiated and received.
Two forces act on the Moon. The force FRradiated by the Earth in the past and the recoil force FRecoil. These two forces are equal to the mass of the Moon times its acceleration. Thus, the formulation is causal.
S. Carlip [13] , I J. Good [14] , and A. P. Lightman et al. [15] , state: “It is certainly true, although perhaps not widely enough appreciated, that observations are incompatible
![]()
Figure 1. A gravitational force FR was radiated in the past by the Earth shown in turquoise and is sensed currently by the Moon shown in gray. A gravitational force FA is radiated currently by the Moon shown in gray that might or might not be sensed in the future by the Earth shown in pink. By Newton’s law of action and reaction the Moon experiences a recoil force FRecoil currently equal in magnitude and opposed to the force FA that the Moon radiated. The Moon will experience the recoil force FR ecoil whether or not the force FA that the Moon radiated will arrive at its destination. The recoil force is causal. Thus, the forces that the Moon experiences currently FR and FRecoil are causal.
with Newtonian gravity with a light-speed propagation delay added in. .... it is known that Solar System orbits would shift substantially on a time scale on the order of a hundred years.” The calculations that led to this erroneous conclusion only used the retarded part of the interaction. To correctly calculate the motion of a system where the interaction propagates with a finite velocity between objects both the retarded and re- coil parts of the equation of motion have to be used. The recoil force is equal in magnitude to the advanced force. In the delayed gravitational interaction the recoil terms cancel the first order terms of the retarded terms leaving only small second order terms. Thus, a few percent shifts in the orbits occur in the order of 107 years. As discussed above, the apparent non causal advanced term is actually equal to a causal recoil term by Newton’s principal that states that for every action there is an equal and opposed reaction.
A delayed interaction central force problem for electrical charges has been discussed by many eminent scientists including Carl Friedrich Gauss (1845), K. Schwarzschild (1903), W. Ritz (1908), H. Tetrode [16] (1922), A. D. Fokker (1929), P. A. M. Dirac [17] (1938), J. H. Wheeler and R. Feynman [18] (1945), R. V. Kamat [19] (1970), A, Lande [20] (1950), K and M Imaeda (1982), etc. All have used both advanced and retarded interaction components in their calculations.
Carl Friedrich Gauss in 1845 was the first scientist recorded to discuss interactions at a distance that propagate with a finite velocity.
Electromagnetic Theory texts discuss the force on an accelerating charged particle due to the radiation emitted by it [21] [22] [23] . It is only necessary to use one part of the interaction, if there are no other charges that radiated interactions in the past that the particle is currently sensing. The radiation generated by the accelerating particle is described by the advanced term of the model used here. Panofsky and Phillips mention an advanced interaction but discard it on the grounds that it is non causal [23] .
Newtonian Mechanics works exceedingly well in providing a mathematical model for a very large number of physical phenomena. However, there are physical phenomena where the Newtonian mathematical model is insufficient [24] . Various attempts were made to provide modified mathematical models. One such model was proposed by Mordehai Milgrom [24] [25] of the Weizmann Institute in Rehovot, Israel in 1983. He proposed a Modified Newtonian Dynamics (MOND) as an alternative explanation to “Dark Matter” to explain the motion of galaxies and galaxy clusters.
2. Equation of Motion
2.1. Reference Frame
For the calculations of the motion of the components of our machines made by humans and robots we use the surface of the Earth as an inertial reference. The acceleration of the surface of the Earth is small compared to accelerations of the machine components. The Earth surface moves because the Earth spins about its axis, it orbits about the Sun, the Sun orbits about the galactic center which also is not stationary. There is no absolute stationary reference in the universe.
The center of mass of most systems orbit about some other object such as a star for a moon planet system or the center of a galaxy for star systems. One can approximate this parent system as being an inertial reference frame. The orbital velocity of this parent system is assumed to be constant and uniform for the duration of one cycle of the system whose motion is being analyzed.
For the calculation of the Moon Earth system the center of mass of the Earth Sun system is used as the approximate inertial reference coordinate system. The center of mass velocities of the Earth Sun system are assumed to be approximately constant. It is further assumed that the center of mass of the Earth Sun system moves slowy compared to the orbital motion of the Moon Earth system. This is similar to the Born Oppenheimer approximation [26] .
2.2. Derivation of the Equation of Motion
The motion of the objects with a delayed interaction can be derived from a method similar to the Euler Lagrange model. One can develop a causal Lagrangian Lk that contains the effect of the delayed gravitational interaction. Since the propagation time of the gravitational interaction is very short compared to the orbital period one can extend the Lagrangian L of the centrally symmetric Kepler problem [2] to include the propagation delay effect.
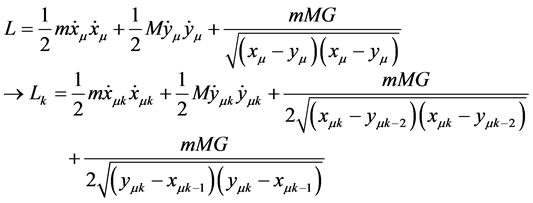 (2.1)
(2.1)
where summation over repeated Greek indices is implied. The Latin subscripts label discrete times. The single gravitational potential of the Kepler formulation is split into two potentials. The first potential describes a gravitational interaction that was radiated by the Planet in the pastat time tk-2 and is sensed currently at time tk by the Moon. The second potential describes a gravitational interaction that was radiated by the Moon in the past at time tk-1 and is sensed currently at time tk by the Planet. Thus the Lagrangian Lk is causal. As described by Dirac [17] , half of each of these potentials is used.
The Euler Lagrange [2] variational method was used for the derivation of the equations of motion.
The Euler Lagrange [2] method for the derivation of the equations of motion is most readily implemented using tensor notation. Here m is the mass and xµk is a component of the position vector xk of the Moon at time step tk and M is the mass and yµk is a component of the position vector yk of the Planet at time step tk. The time differences such as 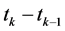 are propagation delays. The
are propagation delays. The 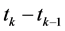 are finite time durations. The time steps such as tk−2, tk−1, tk, tk+1, and tk+2 are not necessarily consecutive. They are just time step labels. The time steps are not integer related. Bold letters such as u denote
are finite time durations. The time steps such as tk−2, tk−1, tk, tk+1, and tk+2 are not necessarily consecutive. They are just time step labels. The time steps are not integer related. Bold letters such as u denote
vectors, single superior dots such as 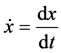 denote time derivatives and double superior dots such as
denote time derivatives and double superior dots such as 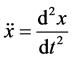 denote second time derivatives.
denote second time derivatives.
To include the effect of both finite and infinitesimal time increments in the derivation of the equation of motion a sum S of Lagrangians Lk is used. The method used here is similar to the discrete Nagumo equation [27] .
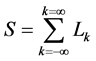 (2.2)
(2.2)
The equations of motion are obtained by inserting the sum of Lagrangians into the Euler Lagrange equations of motion for the Moon and the Planet.
 (2.3)
(2.3)
By using the Lagrangians Lk of Equation (2.1) in the sum of Lagrangians in Equation (2.2) and substituting this sum into Equation (2.3) one obtains the following discrete Nagumo like equation of motion [20] for the Moon and Planet respectively:
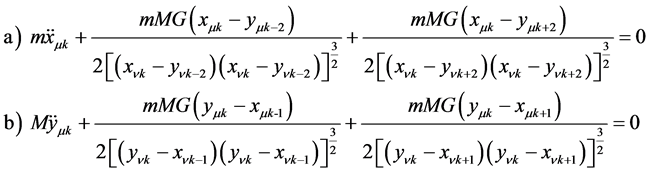 (2.4)
(2.4)
In Equation (2.4) the second terms are the Retarded forces and the third terms are the Recoil forces. By Newton’s principle of action and reaction the Recoil forces are equal in magnitude to the Advanced forces. Note that the second and third forceterms of Equation (2.4) have the same sign and are, therefore in the same direction. Observe that the true Advanced force FA shown in pink in Figure 1. points in a different direction than the Retarded force FR. Thus the third terms of Equation (2.4) are the Recoil force FRecoil. Recall that the Recoil force FRecoil is equal in magnitude to the Advanced force FA. Thus these forces can be mathematically formulated now in terms of future coordinates. Reformulating Equation (2.4) in the more compact vector notation:
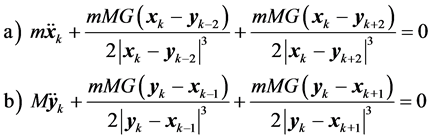 (2.5)
(2.5)
where bold font denotes vectors. The equations of motion contain one half of the Retarded and one half of the Recoil terms as described by Dirac [17] . As stated above the equations of motion are causal, even though the coordinate vectors 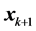 and
and 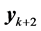 are occurring in the future.
are occurring in the future.
The conventional transformation of variables used in the Kepler problem is as follows [2] :
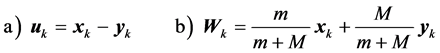 (2.6)
(2.6)
where uk is only approximately the orbital coordinate vector and Wk is, only approximately, the center of mass coordinate vector. By inverting Equation (2.6) one obtains for the current Lunar and Planetary coordinate vectors:
 (2.7)
(2.7)
The propagation time of the gravitational interaction between the objects is very short compared to the orbital period. Since the bodies move only small distances during the propagation time of the gravitational interaction the motion of the objects during this time can be approximated by the product of the current object velocity vectors
 or
or 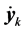 times the interaction propagation time
times the interaction propagation time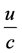 . Here u is the Earth Moon distance and c is the speed of light.
. Here u is the Earth Moon distance and c is the speed of light.
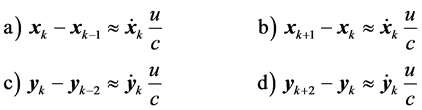 (2.8)
(2.8)
By substituting the transformation of variables of Equation (2.7) into Equation (2.8) one obtains the following approximation for the retarded and recoil vector differences:
![]() (2.9)
(2.9)
For example, the difference in position vectors ![]() of the Moon between times tk and tk−1, is approximated by the center of mass velocity vector
of the Moon between times tk and tk−1, is approximated by the center of mass velocity vector ![]() plus the
plus the
Lunar orbital velocity vector ![]() about the center of mass, times the delay time
about the center of mass, times the delay time![]() . The Moon radiated an interaction at time tk-1 that the Planet is sensing now, at the present, at time tk.
. The Moon radiated an interaction at time tk-1 that the Planet is sensing now, at the present, at time tk.
Because of the form of the approximation of the delayed position differences of Equation (2.9) the time step describing subscripts became unnecessary. By substituting the transformation of variables of Equations (2.6), (2.8) and (2.9) into Equation (2.5) one obtains:
![]()
(2.10)
and
![]()
(2.11)
Since the effects of the delayed interactions are assumed to be small, Equations (2.10) and (2.11) can be expanded to second order in small parameters.
![]() (2.12)
(2.12)
and
![]() (2.13)
(2.13)
The first three terms of Equations (2.12) and (2.13) are the conventional terms of the Kepler problem. The justification for the expansion in small parameters is that the remaining terms of Equations (2.12) and (2.13) are multiplied by the ratios of the
Schwarzschild radii [28] ![]() or
or ![]() divided by the orbital radius u. This ratio is an exceedingly small number.
divided by the orbital radius u. This ratio is an exceedingly small number.
2.3. Equation of Motion of Orbital Radius
The radial equation of motion can be calculated by subtracting Equation (2.13) from Equation (2.12) and dot multiplying the resulting expression by![]() .
.
![]() (2.14)
(2.14)
where ![]() is the reduced mass and the Schwarzschild radii rssR and rssT are:
is the reduced mass and the Schwarzschild radii rssR and rssT are:
![]() (2.15)
(2.15)
The first two terms of Equation (2.14) are the conventional Kepler terms and the remaining terms multiplied by the Schwarzschild radii are due to the delayed interaction.
The angular equation of motion is obtained by taking the cross product of the orbital radius u with the difference of Equation (2.13) minus Equation (2.12)
![]() (2.16)
(2.16)
The orbital coordinate vector u can be expressed in the form of cylindrical coordinates. It is assumed that the center of mass motion is much slower than the orbital motion. Therefore, for the calculation of the orbital motion the center of mass velocity can be approximated by the almost constant velocity V of the reference frame.
![]() (2.17)
(2.17)
By substituting Equation (2.17) into Equation (2.16) and multiplying by ![]() one obtains:
one obtains:
![]() (2.18)
(2.18)
where V is assumed to be a constant and uniform velocity approximately equal to the average velocity of the Earth in its Solar orbit. The “1” direction is taken to be in the direction of this Earth velocity. The Earth Lunar system center of mass moves with respect to this reference frame.
One can neglect the Schwarzschild radius of the reduced mass rssR compared to the orbital radius r in the first term and approximate the radius r in the last term of Equation (2.18) by the radial amplitude aA. With these approximations, Equation (2.18) becomes an exact differential. The radial amplitude aA is not the same as the semimajor axis a.
![]() (2.19)
(2.19)
where ![]() is a constant of integration. Observe that the orbital angular momentum density
is a constant of integration. Observe that the orbital angular momentum density ![]() is not conserved as shown in Equation (2.19b). Since the ratio of the Schwarzschild radii rssR and rssT to the orbital radius r is very small the orbital angular momentum density will differ only very little from the Kepler angular momentum density
is not conserved as shown in Equation (2.19b). Since the ratio of the Schwarzschild radii rssR and rssT to the orbital radius r is very small the orbital angular momentum density will differ only very little from the Kepler angular momentum density![]() .
.
Equation (2.19b) can be used to express the time derivatives of the orbital radius in terms of derivatives with respect to the angle θ to lowest order in small parameters. This is standard procedure in the solution of the Kepler problem.
![]() (2.20)
(2.20)
In returning to the equation of motion of the orbital radius the first step is to substitute the transformation of variables of Equation (2.17) into Equation (2.14).
![]() (2.21)
(2.21)
In order to calculate the values of the orbital radius as a function of the angle the time derivatives of r were formulated in terms of the derivatives with respect to the angle θ in Equation (2.20). This is common practice at this stage of the calculation. As stated before, since the center of mass motion is much slower than the orbital motion, it is assumed that for the duration of one orbit, the center of mass velocity remains constant. By substituting Equation (2.20) to lowest order into Equation (2.21) and multip-
lying the result by ![]() one obtains:
one obtains:
![]() (2.22)
(2.22)
The first three terms of Equation (2.22) are the familiar Kepler equation of motion. The remaining terms, which are multiplied by various Schwarzschild radii, are due to the delayed interaction. Assuming the following solution of this differential equation:
![]() (2.23)
(2.23)
The first term of Equation (2.23a) is the solution of the Kepler problem. Here q is assumed to be a small dimensionless parameter. aA is the orbital amplitude not the semimajor axis. By substituting Equation (2.23) to lowest order in small parameters into Equation (2.22) multiplying by the orbital amplitude aA and collecting terms of equal orbital frequency one obtains:
![]() (2.24)
(2.24)
where
![]() (2.25)
(2.25)
and where Equations (2.19b) and (2.23b) were used in Equation (2.25b) to obtain Equation (2.25c).
Note that A1 in Equation (2.24) is the amplitude of a term oscillating at the resonant frequency of the orbital system. The orbital motion pumps the contribution of the motion due to the delayed gravitational interaction by periodically changing the delay time
![]() as the system orbits. The delay only changes if the orbit is eccentric. Indeed, the
as the system orbits. The delay only changes if the orbit is eccentric. Indeed, the
amplitude A1 is proportional to the eccentricity ε. When the eccentricity is equal to zero there is no increase in the orbit. One can use the Laplace transform method to obtain the following solution of Equation (2.24):
![]() (2.26)
(2.26)
Substituting Equation (2.26) into Equation (2.23a) and multiplying by aA to obtain a solution for the orbital radius as a function of
![]() (2.27)
(2.27)
An important result is that the fourth term on the right side with amplitude ![]() of
of
Equation (2.27) continually increases with the angle θ. Since the angle θ increases monotonically with time, this term and the orbital radius r increase with time. This is one of the main results obtained in this article. It is the contribution to the increase of the orbital radius r due to the delayed gravitational interaction. The increase per orbit is small, it is of the order of the ratio of the Schwarzschild radius divided by the semimajor axis. For example, the Lunar orbit increases by 38 mm per Earth year [29] due to all effects, including the tidal effect. Here A2 and A3 are small amplitudes of the second and third harmonic terms. Equation (2.27) can also be written as:
![]() (2.28)
(2.28)
where
![]() (2.29)
(2.29)
The precession angle is the angular change in the position of the major axis of the orbital ellipse. This can be calculated from Equation (2.29)
![]() (2.30)
(2.30)
An important result shown in Equation (2.28) is that the second term in the square root depends on the square of the orbital angle. Since the orbital angle θ increases monotonically with time the effective eccentricity and the semimajor axis also increase with time. This effect is very small since the constants A0, A1, A2 and A3 are very small.
The constants A0, A1, A2 and A3 can readily be calculated from the knowledge of the masses of the objects and the average Earth velocity in its solar orbit. However, there are two more constants, the offset angle θoffset, and the constant ε. The offset angle θoffset is the present value of the angle θ. The fact that the angle θoffset has a non zero value implies that the current expansion of the Lunar semimajor axis describable by an analytical model started a fixed time ago. For the Lunar orbit there is sufficient information in the form of the change of the semimajor axis per Earth year and the current values of the eccentricity from which these values can be calculated.
The calculations have to be performed numerically. The results of these calculations are given in the RESULTS section. Defining the current eccentricity ![]() from Equation (2.28) as:
from Equation (2.28) as:
![]() (2.31)
(2.31)
The amplitude A2 and A3 of the second and third harmonics are very small compared the eccentricity![]() . Therefore the second and third harmonic terms are neglected. The current value aC of the semimajor axis a is:
. Therefore the second and third harmonic terms are neglected. The current value aC of the semimajor axis a is:
![]() (2.32)
(2.32)
By expanding the semimajor axis of Equation (2.32b) in a Taylor series in θoffset to lowest order one can calculate the current change ![]() in the semimajor axis per lunar orbit:
in the semimajor axis per lunar orbit:
![]() (2.33)
(2.33)
The numerical results of these calculations are given in the RESULTS section.
2.4. Equation of Motion of the Center of Mass Coordinates
The energy lost by the orbital motion is transferred to the center of mass motion. This will cause the center of mass to accelerate. The acceleration of the center of mass can be
calculated by multiplying Equation (2.12) by ![]() and Equation (2.13) by
and Equation (2.13) by![]() , adding the resulting expressions and dot multiplying the result by
, adding the resulting expressions and dot multiplying the result by![]() . Where W is only approximately the center of mass position vector.
. Where W is only approximately the center of mass position vector.
![]() (2.34)
(2.34)
where Equation (2.15a) was used for the Schwarzschild radius rssR. The center of mass coordinates can be expressed in cylindrical coordinates.
![]() (2.35)
(2.35)
Equation (2.34) can be expressed in cylindrical coordinates by substituting Equations (2.17a), (2.17b) and (2.35) into Equation (2.34).
![]() (2.36)
(2.36)
The term multiplied by the Schwars child radius rssR is very small. One can assume that the center of mass velocity changes by a small quantity from its value V which it has in its orbit about the sun. Thus, inside the curly bracket of Equation (2.36) one can approximate the radial component ![]() of the center of mass and the component
of the center of mass and the component ![]() in the direction of the center of mass solar orbit by:
in the direction of the center of mass solar orbit by:
![]() (2.37)
(2.37)
By substituting Equations (2.37) into the curly bracket of Equation (2.36) one obtains.
![]() (2.38)
(2.38)
Substituting Equation (2.20) for the time derivatives of the orbital radius r in terms of the derivative of the orbital radius with respect to the angle θ to lowest order into Equation (2.38).
![]() (2.39)
(2.39)
Substituting Equation (2.23a) to lowest order for the reciprocal radius ![]() into Equation (2.39).
into Equation (2.39).
![]() (2.40)
(2.40)
Since the orbital motion is much faster than the center of mass motion the average value over the orbital angle θ is used to calculate the average center of mass acceleration.
![]() (2.41)
(2.41)
where ![]() denotes the average value of
denotes the average value of![]() .
.
Another equation for the acceleration of the center of mass can be obtained by multiplying Equation (2.12) by ![]() and Equation (2.13) by
and Equation (2.13) by![]() , adding the re-
, adding the re-
sulting expressions and cross multiplying the result by the center of mass coordinate vector W.
![]() (2.42)
(2.42)
Reformulating Equation (2.42) in cylindrical coordinates by substituting Equations (2.17a), (2.17b) and (2.35) into Equation (2.42).
![]() (2.43)
(2.43)
where Equation (2.15a) was used for the Schwarzschild radius rssR. By using the approximations of Equations (2.37) in the curly bracket of Equation (2.43) one obtains:
![]() (2.44)
(2.44)
Substituting Equations (2.20) for the time derivative of the orbital radius r in terms of its derivative with respect to the angle θ to lowest order into Equation (2.44).
![]() (2.45)
(2.45)
Substituting Equation (2.23) to lowest order for the reciprocal radius ![]() into Equation (2.45).
into Equation (2.45).
![]() (2.46)
(2.46)
Similar to Equation (2.40), since the orbital motion is much faster than the center of mass motion the average value over the orbital angle θ is taken.
![]() (2.47)
(2.47)
Multiplying Equation (2.47) by ![]() in order to put Equation (2.47) in the form of an exact differential.
in order to put Equation (2.47) in the form of an exact differential.
![]() (2.48)
(2.48)
First using the approximations of Equations (2.37) in Equation (2.48). Then the resulting equation can be reformulated in the form of an exact differential.
![]() (2.49)
(2.49)
where L is a constant of integration. Solving Equation (2.49b) for![]() .
.
![]() (2.50)
(2.50)
By substituting Equation (2.50) for ![]() into Equation (2.41) one obtains the equation of motion of the center of mass.
into Equation (2.41) one obtains the equation of motion of the center of mass.
![]() (2.51)
(2.51)
where ![]() is the centrifugal force associated with the center of mass motion. Equa-
is the centrifugal force associated with the center of mass motion. Equa-
tion (2.51) for the acceleration of the center of mass ![]() is another important result. For the simple Newton Kepler orbit, the center of mass acceleration is equal to zero.
is another important result. For the simple Newton Kepler orbit, the center of mass acceleration is equal to zero.
3. Results
3.1. Earth Moon System
There is sufficient data available to calculate the offset angle and the time period corresponding to the offset angle. The annual increase in the orbital radius of the Moon has been measured by NASA [29] using a retroreflector left on the Moon by Apollo 11. The data from the literature for the calculation of the motion of the Earth Moon system is listed in Table 1. The calculated parameters such as the constants A0, A1, A2, and A3, etc. are listed in Table 2. The analytically calculable start of the present expansion of the semimajor axis started 2.926237 Million years ago. Perhaps the Moon collided with a large enough object 2.926237 Million years ago to alter its orbit and obscure its pre-
vious analytical motion. The contribution of the delayed gravitational interaction to the Apsidal precession of the Lunar orbit is 83.83185072 µarc seconds.
A plot of the predicted contribution of the delayed gravitational interaction to the length of the semimajor axis of the Lunar orbit is shown in Figure 2. Note that the expansion of the semimajor axis started 2.926237 Million years ago. Perhaps at that time an object collided with the moon to effect its orbit enough to obscure its previous analytical describable motion.
The contribution of the delayed gravitational interaction to the eccentricity of the Lunar orbit is shown in Figure 3.
The loss of the orbital energy is transferred to the center of mass motion. This will cause the center of mass to accelerate. A plot of the center of mass acceleration is shown in Figure 4. The predicted current acceleration = 2.51414022 × 10−16 m per second squared.
![]()
Figure 2. This is a plot of the predicted contribution of the delayed gravitational interaction to the length of the semimajor axis of the Lunar orbit. Considering only the effect of the delayed gravitational axis, the semimajor axis had a length of 384,395,194.9 m 2.926237 Million years ago. This analytically describable expansion of the semimajor axis started 2.926237 Million years ago. Perhaps at that time something collided with the moon to effect its orbit enough to obscure its previous analytical describable motion.
![]()
Figure 3. The contribution of the delayed gravitational interaction to the eccentricity of the Lunar orbit.
![]()
Figure 4. A plot of the center of mass acceleration due to the loss of the orbital energy.
3.2. The Brown Dwarf 569Bab System
Another interesting system that can readily be analyzed is the Brown Dwarf Binary system 569Bab. Lane [30] [31] et al. measured many parameters of this system. Measurements to date show that this system consists of a pair of Brown Dwarfs 569Ba and 569Bb orbiting about the star 569 A. The system is located 9.8 pc or 3.023964 × 1017 m. from us. The radius of the orbit of the Brown Dwarf pair 569B about the star 569A as seen from Earth is about 5” or 49 AU or 7.330295635 × 1012 m. The pair 569B orbits about the star 569A in 15 years. The Brown Dwarf system 569Ba and 569Bb has a combined mass of 0.123 solar masses and a mass ratio of 0.89. The Brown Dwarfs orbit about each other in ![]() days at a semimajor axis a of
days at a semimajor axis a of ![]() AU. The eccentricity of the orbit of the Brown Dwarfs around each other is
AU. The eccentricity of the orbit of the Brown Dwarfs around each other is![]() . The age of this system is estimated to be only 3 × 108 years. The data from the literature for the calculation of the motion of the Brown Dwarf star pair 569Bab is listed in Table 3. The calculated parameters such as the constants A0, A1, A2, and A3, etc. are listed in Table 4.
. The age of this system is estimated to be only 3 × 108 years. The data from the literature for the calculation of the motion of the Brown Dwarf star pair 569Bab is listed in Table 3. The calculated parameters such as the constants A0, A1, A2, and A3, etc. are listed in Table 4.
There is not sufficient data to accurately calculate the analytically calculable start of the expansion of the semimajor axis. The earliest time of the analytically calculable start of the expansion of the semimajor axis is 8.9271548613 Million years ago. This is a maximum value. It could have started at a later time. Perhaps one of the brown dwarf stars collided with a large enough object 8.9271548613 Million years ago or later to alter its orbit and obscure its previous analytical motion.
A plot of the predicted contribution of the delayed gravitational interaction to the length of the semimajor axis of the orbit of the 569Bab system is shown in Figure 5. Note that the analytically describable expansion of the semimajor axis could have
![]()
Figure 5. A plot of the predicted contribution of the delayed gravitational interaction to the length of the semimajor axis of the 569Bab system orbit. This analytically describable expansion of the semimajor axis could have started as early as 8.927154154 Million years ago or at a shorter time. Perhaps at that time something collided with the dwarf stars to affect their orbit enough to obscure its previous analytical describable motion.
![]()
Table 4. 569Bab system data constants.
started as early as 8.927154154 Million years ago or at a shorter time. Perhaps at that time an object collided with one of the two Brown Dwarf stars that effect the orbit enough to obscure its previous analytical describable motion.
The contribution of the delayed gravitational interaction to the eccentricity of the orbit of the 569Bab Brown Dwarf stars is shown in Figure 6.
The loss of the orbital energy is transferred to the center of mass motion. This will cause the center of mass to accelerate. A plot of the center of mass acceleration is shown in Figure 7. The predicted current acceleration of the center of mass of the Brown Dwarf 569Bab system is 5.54963756 × 10−14 m per second squared.
![]()
Figure 6. The contribution of the delayed gravitational interaction to the eccentricity of the 569Bab system orbit.
![]()
Figure 7. A plot of the center of mass acceleration of the 569Bab system due to the loss of the orbital energy.
Again, it is assumed that the radius of the orbit of the pair about the star 569A is large compared to the orbit of the Brown Dwarfs about each other. Thus, this orbital velocity is assumed to be the approximate constant center of mass velocity of the Brown Dwarfs.
4. Conclusions
The small effect of the propagation delay of the gravitational interaction on the motion of the Earth Moon and the Brown Dwarf 569Bab binary star systems were calculated. The calculated values are in very good agreement with observed values.
Recent measurements have shown that gravitational waves and thus the gravitational interactions propagate with the speed of light. The gravitational propagation delay exists whether the interaction is modeled by the deformation of the four dimensional space due to the mass of the bodies, or it is modeled by a gravitational interaction that is propagating between objects. In each case a change in position of one object takes time to be sensed by the other object.
The delayed interactions between two objects are causal. The single interaction force of the model that considers interactions to be instantaneous is split into two forces in a model that takes the propagation delay of the interaction in consideration. Object ONE senses currently a force radiated by object TWO in the past, see Figure 1. This is the Retarded force. Object ONE radiates a force currently that might or might not be sensed by object TWO in the future. This is an advanced force. Object ONE experiences a Recoil force currently equal in magnitude and opposed in direction to the advanced force it radiated. Thus object ONE experiences two forces, the Retarded force and the Recoil force both of which are causal. The objects experience the forces continually.
The propagation delay of the gravitational interaction couples the orbital and center of mass coordinates of orbiting systems. The propagation delay between objects varies periodically for systems with eccentric orbits. The periodically changing propagation delay pumps the motion of the objects. This causes both the eccentricity and orbits to grow and loose energy. The loss in orbital energy is transferred to the center of mass motions. Thus, the center of mass accelerates. These effects are very small. The semimajor axis of the Lunar orbit grows by 38 mm per Sidereal year and the center of mass acceleration is a fraction of a pico meter per second squared.
By using the present astronomical data one obtains that the growth of the orbital axis and eccentricity started at a time shorter than the age of the systems. This can, perhaps, be explained by one of the system components having had a collision that erased the previous analytically describable motion.
All orbiting systems in the universe convert some of their orbital energy to its center of mass motion. The center of mass acceleration of the various orbiting systems is in random directions. One can consider the very large number of star systems, galaxies, and galactic clusters as molecules in the universe. The transfer of internal orbital energy to the molecular motion will increase the entropy, temperature and pressure of the gas. The gas will expand. Alternatively, one should include the change in orbital energy with the energy and mass of the Universe in the calculation of the accelerating expansion of the Universe.
It is not known if this contribution is enough to explain the present accelerating expansion of the Universe [4] . But if correct, the so far undetected Dark Energy and Dark Matter would not be necessary.
Acknowledgements
I thank my wife Marlene Danzig Kornreich for her suggestions to the text and making the text more understandable to a reader.