1. Introduction
Normal distribution occupied an important position on probability theory and mathematical statistics both theoretically and practically. It widely exists in various fields including natural phenomenon, industrial production and high-technology, etc.
Generally speaking, normal distribution is an index influenced by many independent random factors, but each of them only has a tiny effect. For instance, quality indexes of all kinds of products (like size of tools, capacitance of capacitors, strength or tension of fibers), one characteristic of a group (like vital capacity of pupils in a class, plant length or stem diameter of rice in one area), or measured data of events (like the highest air temperature, average rainfall or humidity). All the indexes above are approximately obey the normal distribution.
However, as the development of science, especially the development of computer science and artificial intelligence, we are facing an important issue: how to use mathematical language to express human thinking. So after the birth of fuzzy mathematics in 1956, and a lot of combinations between fuzzy numbers and other mathematical theories were built rapidly. The fuzzy language is a method to transform natural language into quantification and mathematics, to adapt the needs of computer programs. The fuzziness is the essence of language, with which rich emotion can be expressed. In mathematical statistics, “may-occur”, “very-likely-occur” or “rarely-occur” are vague expressions, but we can use the fuzzy membership function to quantify, and fix them into the calculation of the normal distribution.
CM Stein published in 1981 that using sum of squared errors as loss, estimation of the ways of normal in dependent random variables is advised, then he suggested that mean vector centered at an arbitrary estimate could be an application of calculating approximate sets [1] . In 2007, Mikl applied normal distribution for statistics on the Stirling Permutation defined by Gessel and Stanley, he equidistributed statistics on these objects converge to a normal distribution [2] . Even recently, CFF Karney published an algorithm for sampling from the normal distribution exactly, whose parameters are rational numbers, thereafter uniform random digit are copied into the representation directly [3] . Ever since the built of fuzzy maths, it’s application with calculation algorithm has been prospered [4] - [9] .
Traditional normal distribution can only calculate the determined indexes, such as “40 degrees Celsius” or “120 pounds” or “45 years old”. But the uncertain concepts of data which can be represented by fuzzy number, like “appropriate temperature”, “normal weight” or “middle-aged”, also need to be count. So in this paper, we provide a model to calculate the fuzzy concepts’ probability by the integral of normal distribution probability density function.
2. Fuzz Formula
The traditional normal distribution formula is showed below:
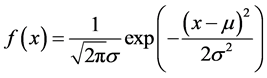
In this formula, the “μ” is defined as the expectation of a random event, and the “σ” is defined as the variance of a random event, they are identified when dealing with a determinate question. Usually the “x = g” should be a specific number when we check a certain concept, and f(x) can be calculated by determinate automaton but the “g” sometimes can be calculated as a fuzzy number. Fuzzy numbers are discussed in the interval number’s basis, the interval number is considering a closed interval [A, B] as a number of processing, Each independent variable x in [A,B] is mapped to the corresponding normal distribution density value, and at the same time, it also satisfies the corresponding membership function. So the integral of 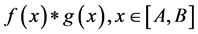 is the probability of fuzzy number.
is the probability of fuzzy number.
We set H(x) as the probability value of fuzzy number “g”, so:
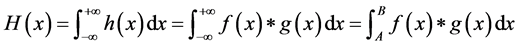
And this paper gives three examples:
2.1. May-Occur Events
As the standard normal distribution table, the integral quantity from φ(−0.5) to φ(0.5) is 0.383, and the value from φ(−1) to φ(1) is 0.6826 (see Figure 1).
So the possibility between 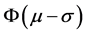 and
and 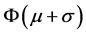 occupy mostly, and the events
occupy mostly, and the events 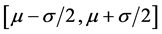 can belong to the “may-occur event”. In this paper, we defined the result of membership function between
can belong to the “may-occur event”. In this paper, we defined the result of membership function between 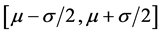 is 1, And the result of membership function between
is 1, And the result of membership function between 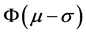 and
and 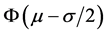 as well as events between
as well as events between 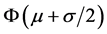 and
and 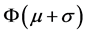 are lifting from zero as it approach to the middle, so according to the knowledge in fuzzy maths we defined it changes as quadratic function (see Figure 2).
are lifting from zero as it approach to the middle, so according to the knowledge in fuzzy maths we defined it changes as quadratic function (see Figure 2).
So the membership function g(x) should be divided into five parts and here we gives the may-occur events’ membership function:
![]()
And its chant is shown in Figure 3.
![]()
Figure 1. The possibility of Normal distribution from Φ(μ − σ/2) to Φ(μ + σ/2).
![]()
Figure 2. The possibility of Normal distribution from Φ(μ − σ) to Φ(μ − σ/2) and from Φ(μ + σ/2) to Φ(μ + σ).
![]()
Figure 3. The membership function of may-occur event.
This kind of model have applications in multiple ways, some broad-loose events like “general quality products in one production” or “normal section of score in a test” which may happen most time we sample, is a result of general research expression.
2.2. Very-Likely-Occur Event
As the standard normal distribution table, the integral quantity from φ(−0.2) to φ(0.2) is 0.1586.
So the event between 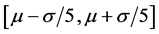 can be called “very-likely-occur event” cause they are surrounding the symmetry axis “x = μ”, and the membership function in this interval would be 1. The interval
can be called “very-likely-occur event” cause they are surrounding the symmetry axis “x = μ”, and the membership function in this interval would be 1. The interval 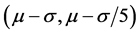 and from
and from 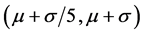 also agree with the power function relationship, but its tendency will change more steeply, we define it as cubic function.
also agree with the power function relationship, but its tendency will change more steeply, we define it as cubic function.
So the very-likely-occur events’ membership function shows below:
![]()
And its chant is shown in Figure 4.
This kind of model have applications in every investigation, the most frequent events like “the time office workers usually get up” or “the speed of one train in one trip” which may happen 90 percent each time we sample, it’s basically distribute around a certain point.
2.3. Rarely-Occur Event
As the standard normal distribution table, the integral quantity from φ(−3) to φ(3) is 0.9974.
So the event between ![]() and
and ![]() can be called “rarely-occur event” cause their probability are almost zero. And member function in
can be called “rarely-occur event” cause their probability are almost zero. And member function in ![]() is 0.
is 0.
![]()
Figure 4. The membership function of very-likely-occur event.
![]()
Figure 5. The membership function of rarely-occur event.
So the rarely-occur events’ membership function shows:
![]()
And its chant is shown in Figure 5.
And this is the model of extreme situation.
3. Case Analysis
In a sports comprehensive evaluation, a class of 50 people’s score shows as follows:
53.6162 55.6079 61.4699 61.9634 64.7698 65.8982 66.3626 66.8872
70.7759 71.1514 72.1262 72.3638 73.5902 74.0450 74.1331 74.1602
75.5567 76.7973 78.0933 78.5431 78.9637 79.1533 80.3374 80.5220
80.5663 80.6490 80.6914 81.0579 81.2104 81.6568 81.7275 82.1617
82.2923 83.6559 83.6559 84.6994 85.2302 85.4510 85.7813 86.4338
86.8235 87.2359 88.7201 88.9829 89.6834 90.4821 90.7801 91.4503 93.5038 99.7933
Fitting these data. The results can be regarded as a normal distribution, with f(x) to represent normal distribution function, g(x) represent the membership functions, the mathematical expectation is approximately 80, the standard deviation of approximately 10, so according to the membership function, ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
1) To get the probability of “normal level” score should based on the “may-occur” model, the operation procedure shows as follows:
![]()
![]()
In this case, “may-occur” events’ probability is 0.492.
2) To get the probability of “very poor level” score should based on the “may-occur” model, and we only use half model which less than expectation, the operation procedure shows as follows:
![]()
![]()
In this case, “”rarely-occur” events’ probability is 0.0048.
These two case also conform to reality. And for all those three models, the result will be changed if μ or σ were recalculated. So if we remove the intervals of event, we will get a different possibility.
4. Conclusions
If other distributed events are all provided, there may be a general model be created to define them. So if we can refine human emotion more specific and meticulous, this model will have a very wide range of applications in the field of artificial intelligence.