The Proof of Hilbert’s Seventh Problem about Transcendence of e+π ()

Subject Areas: Algebra, Algebraic Geometry

1. Introduction
Hilbert’s seventh problem is about transcendental number. The proof of transcendental number is not very easy. We have proved the transcendence of “e” and “π”. However, for over a hundred years, no one can prove the transcendence of “e + π” [1] . The purpose of this article is to solve this problem and prove that e + π is a transcendental number.
2. Proof
1) Assuming 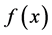 is any one polynomial of degree n.
is any one polynomial of degree n.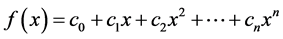 ,
, 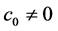 , Let
, Let 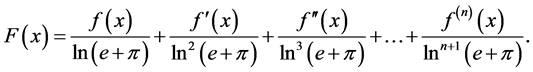
Now we consider this integral: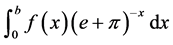 . By integrability by parts, we can get the following For- mula (2.1):
. By integrability by parts, we can get the following For- mula (2.1):
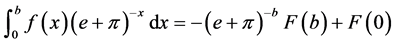 (2.1)
(2.1)
2) Assuming 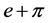 is a algebraic number, so it should satisfy some one algebraic equation with integral coefficients:
is a algebraic number, so it should satisfy some one algebraic equation with integral coefficients: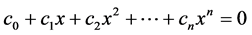 ,
,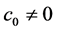 .
.
According to Formula (2.1), using 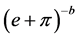 multiplies both sides of Formula (2.1) and let be separately equal to
multiplies both sides of Formula (2.1) and let be separately equal to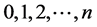 . We get the following result.
. We get the following result.
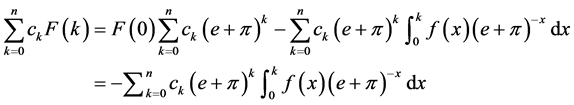 (2.2)
(2.2)
So, all we need to do or the key to solve the problem is to find a suitable 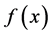 that it doesn’t satisfy the Formula (2.2) above.
that it doesn’t satisfy the Formula (2.2) above.
3) So we let 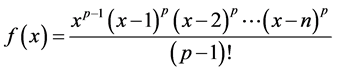 [2] ,
[2] ,  ,
, ![]() and b is a prime number Because of
and b is a prime number Because of![]() ,
, ![]() , so
, so ![]() can be divisible by
can be divisible by ![]() and when
and when![]() , all of
, all of ![]() equal zero.
equal zero.
Furthermore, we consider ![]() whose (p + a)-th derivative (
whose (p + a)-th derivative (![]() ); when
); when![]() , the derivative is zero. And when
, the derivative is zero. And when![]() , the derivative is
, the derivative is![]() . What’s more, the coefficient of
. What’s more, the coefficient of ![]() is a multiple of (p + a)!, so it’s alse a multiple of (p − 1)! and p.
is a multiple of (p + a)!, so it’s alse a multiple of (p − 1)! and p.
By the analysis above, we can know that ![]() are multiples of p.
are multiples of p.
Now we see![]() ; we know,
; we know,
![]()
and its the sum of the first p − 1 item is zero (because the degree of each term of ![]() is not lower than
is not lower than![]() ). All from the (p + 1)-th item to the end are multiples of p. But the p-th item
). All from the (p + 1)-th item to the end are multiples of p. But the p-th item ![]() is the (p − 1)-th derivative of
is the (p − 1)-th derivative of![]() . So,
. So, ![]() , and
, and ![]() and
and ![]() are congruence, written
are congruence, written![]() . Thereby,
. Thereby, ![]() , but
, but![]() ,
, ![]() , and b is a prime number, so
, and b is a prime number, so
![]() ,
,![]() (2.3)
(2.3)
4) Next, we need to prove that ![]() when p tends to be sufficiently large.
when p tends to be sufficiently large.
When x changes from 0 to n, the absolute value of each factor ![]() of
of ![]() is not more than n, so
is not more than n, so![]() ,
,![]() .
.
So by integral property: when![]() ,
,
![]()
Let M equal ![]()
thus, ![]()
When![]() . So,
. So,![]() (2.4)
(2.4)
Finally, according to (2.3) and (2.4), we know (2.2) is incorrect. So, e + π is a transcendental number.
3. Conjecture
By the proof above, we conclude that e + π is a transcendental number. Besides, I suppose ![]() is also a transcendental number. What’s more, when a and b are two real numbers, and
is also a transcendental number. What’s more, when a and b are two real numbers, and![]() , I suppose that
, I suppose that ![]() is a transcendental number.
is a transcendental number.
Acknowledgements
I am grateful to my friends and my classmates for supporting and encouraging me.