Subject Areas: Geometry, Geometry Education
1. Introduction
Bilindiği üzere, ortaokul ve liselerin geometri derslerinde okutulan öklid geometrisinde nokta ile doğru bu düzlem geometrisinin esas kavramlarıdır.
Resim 1. Öklid geometrisinin temeli.
Herhangi bir M noktası l doğrusu üzerinde olursa
, doğru M noktasından geçer ve iki nokta doğrunun üzerinde yer alır. Öklid geometrisinde her hangi iki doğru parçası sadece iki durumda bulunabilir.
1. durum: Eğer bu doğruların ortak noktaları varsa kesişirler.
Resim 2. l1, l2 kesişen doğrular.
2. durum: Eger l1, l2 doğrularının ortak noktaları yoksa bu doğrular kesişmez ve birbirlerine paraleldirler.
Resim 3. l1, l2 paralel doğrular.
M noktası l doğrusunun üzerinde değilse, M noktasından geçen doğru destesi içerisinden sadece bir tanesi l doğrusuna paraleldir.
Resim 4. l, l1 paralel doğrular.
Yukarıda ifade edilen kavramlar, Öklid geometrisi düzlemi olarak okullarımızda öğretilmektedir. Burada Öklid aksiyomları onun temel esaslarını teşkil eder. 1829 yılında N.I. Lobaçevski, Geometriye bir yenilik olarak paralellik aksiyomunu ilave eder ve kendisinin bu katkısını “Tasavvurdaki Geometri” olarak adlandırır.
Bu aksiyom (Lobaçevski aksiyomu); Bir doğruya üzerinde bulunmayan noktadan kesişmeyen iki doğru çizilebilir, şeklinde ifade edilir.Amacımız Lobaçevski aksiyomunun geçerli olduğu noktalar kümesini göstere- bilmektir. Bunun için sadece Öklid düzleminden faydalanılacaktır. Bilindiği gibi, Öklid düzlemi sonsuz bir şekilde bütün yönlere uzayıp gider.
Her ne kadar, düzlemin tamamını hayal etmemiz mümkün olsa bile bunu görmemiz mümkün değildir. İnsanın görüş imkanı sınırlandırılmıştır. Öklid düzleminin görünebilirliği mümkün olan noktalarını Lobaçevski düzle- minin noktaları olarak alalım. Bu düzlemdeki doğruların görme mesafesine giren bölümüne Lobaçevski düzle- minin doğruları diye bakabiliriz. Eğer görüş sahamız daire şeklinde olsa aşağıdaki şekil meydana gelir [1] .
Resim 5. Lobaçevski düzlemi.
Normalde düzlemin mavi boyalı kısmı bize görünmemektedir. Demek ki Lobaçevski düzleminin noktalarına, daire içindeki noktalar ve doğrularına kirişler diye bakacak olursak T1 ve T2 doğrularının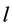 
doğrusuyla kesiş- mediğini açık bir şekilde görüp söyleyebiliriz. Buradan da Lobaçevski aksiyomunun sağladığını yani söylenen doğrularda l doğrusuyla kesişmeyen T1 ve T2 doğruları gösterilmiş olur.
Resim 5’deki;
・ 
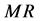doğrusu l doğrusuyla kesişir.
・ 
doğrusu ile l doğrusunun kesişme noktası dairenin kenar noktasında bulunur.
・ l1 doğrusu l doğrusuyla kesişmemektedir.
Lobaçevski aksiyomundan faydalanarak aşağıdaki teoremler ispatlanabilir.
Teorem-1: Bir doğru üzerinde olmayan herhangi bir noktadan doğru ile kesişmeyen sınırsız sayıda doğru çizilebilir. Bunu aşağıdaki resimde görebiliriz.
Resim 6. Kesişmeyen doğrular.
Gerçekten; T1 ve T2 doğruları dışarıda çizilen doğrulardan oluşan dikey açıdan geçen herhangi bir doğru l ile kesişmemektedir. M noktasından geçen doğrular arasında l doğrusu ile kesişen ve kesişmeyen doğrular mev- cuttur [2] .
Tanım: M noktasından geçen ve l doğrusu ile kesişen ve kesişmeyen doğrular toplamını sınırlayan doğruya l doğrusuna paralel doğru denir. Bu tanım aşağıdaki teoremi doğrulamaktadır.
Teorem-2: l doğrusunun dışında M noktasından l’ye paralel iki doğru çizebiliriz.
Resim 7. Paralel doğrular.
Paralel doğrular iki türlü olduğundan, bunların farklarını, sağdan paralel ve soldan paralel tanımlarıyla ifade edebiliriz.
Resim 8. Soldan paralel doğrular.
Resim 9. Sağdan paralel doğrular.
Şimdi verilen bir l doğrusuna sağdan ve soldan paralel doğrular çizelim.
Resim 8 ve Resim 9’da paralel doğrular tasviri, ve Resim 10’da Öklid geometrisindeki paralel doğruların Lobaçevski geometrisindeki ifadesi gösterilmektedir.
Resim 10. Öklid paralelleri.
Lobaçevski düzlemini ifade edebilmek için görme mesafesini esas almıştık. Resim 10’daki paralel doğrulara sağdan veya soldan bakılırsa Lobaçevski paralelliğini tasavuur edebiliriz. Örneğin, şu demiryolunun ortasından bakınca paralel doğruların uzakta kesişiyor görülmesi gibi.
Resim 11. Demiryolunun görünüşü.
2. Paralelliğin Özellikleri
Lobaçevski doğrularının Öklid doğrularından farklı olduğu aşağıdaki özelliklerden anlaşılabilinir [3] .
1) Eğer l1 doğrusu l2 doğrusuna paralel olursa l1―den alınan herhangi bir M noktasından l2 ye kadar olan mesafe parallelik yönünde azalır ve ters yönde artar. Öklid düzleminde ise paralel doğrular arasındaki mesafe değişmez.
Resim 12. Paralellik mesafesi.
2) Bilindiği gibi Lobaçevski düzleminde herhangi bir doğru, düzlemi iki yarım düzleme ayırır. Bu özellik Lobaçevski düzlemini doğrulamaktadır.
![]()
Resim 13. Lobaçevski düzleminin bölünmesi.
3) Paralel l1 ve l2 doğruları verilsin l1 doğrusundan l2 yedik doğrularçizdiğimizde bu dikliklerintabanı l2―de doğruları tam kaplamayabilir.
![]()
Resim 14. Kaplanmayan alan.
4) Lobaçevski düzleminde üç doğru kesişmesinden meydana gelen şekli üçgen olarak alacak olursak, iki kenarı kendi arasında paralel (Resim 15(A)), iki çift kenarı paralel (Resim 15(B)) ve üç kenarı paralel (Resim 15(C)) üçgenler mevcuttur.
![]()
(A) (B) (C)
Resim 15. Kesişen Üçgenler.
Lobaçevski düzlemindeki açı ile Öklid düzlemindeki açı kavramları aynıdır.
5) Öklid düzlemindeki paralel doğrular Lobaçevski düzleminde kesişmeyen doğrulardır.
![]()
Resim 16. Öklid Lobaçevski paralelleri.
6) l1 ve l2 Lobaçevski düzleminin kesişmeyen doğruları olsun, bu doğrular için yalnız genel bir diklik mev- cuttur ve bu da doğrular arasındaki mesafeyi verir.
![]()
![]()
(a) (b)
Resim 17. Lobaçevskide mesafe tasavvuru.
Lobaçevskinin bu özelliğini anlamak için Resim 17B’yi göz önüne getirmek gerekmektedir. O zaman sınırlanmış MN arasını en kısa mesafe olarak anlamak mümkündür.
7) Lobaçevski düzlemindeki paralelliği göz önüne getirmek için genel asimtota sahip olan bir hiperbol gra- fiğini tasavvur edebiliriz.
![]()
![]()
(a) (b)
Resim 18. (A) Lobaçevskide paralellik; (B) Lobaçevskide paralellik tasavvuru.
3. Sonuç
Özellikle lise öğrencilerinin geometri derslerinde ufuklarını açmak üzere, bilinen ve yaygın bir şekilde kullanıl- makta olan öklid geometrisinden faydalanarak Lobaçevski aksiyomu ve düzlemi öğrencilere izah edilmeye çalışıldı. Özellikle görüş mesafesi kavramından ve demiryolu örneğinden öğrencilerin tasavvurdaki geometri üzerine bakışlarının değiştiği gözlemlenmiştir.