Estimating the Frequency, Magnitude and Recurrence of Extreme Earthquakes in Gulf of Aqaba, Northern Red Sea ()
Received 11 April 2016; accepted 28 May 2016; published 31 May 2016

1. Introduction
One of the most destructive disasters of nature is a severe earthquake and its destroying effects. If the earthquake occurs in a populated area, it may cause many deaths and injuries and extensive property damage regions. The ultimate goal of seismic hazard assessment and risk evaluation for a particular site or area is to condense seism-tectonic knowledge and experience into parameters used for predicting seismic parameters which in turn can be applied by engineers in design and subsequent earthquake resistant construction.
Statistical surveys support researches on the likelihood of future earthquakes. A primary goal of earthquake research is to increase the reliability of earthquake probability estimates. With a greater understanding of the hazard parameters of earthquakes, we may be able to reduce damage and loss of life from this destructive event. Statistics help us to predict the future events based on previous events.
1.1. Seismicity of the Western Region of Saudi Arabia
Recently, there has been an increasing concern about the seismic activity along the western coast of the Kingdom. Several studies were conducted to estimate the level of the seismic risk in the Kingdom [1] and [2] . Western Region of Saudi Arabia is considered to be a moderately active seismic zone as shown in Figure 1 [3] . Seismic events in the region that have been reported in literature include a significant earthquake, with a magnitude of 6.25 in Richter scale (a scale for expressing the magnitude of an earthquake in terms of the logarithm of the amplitude of the ground wave; values range from 0 to over 9), that occurred in 1941 at about 30 km to the east of Jizan city [4] . Seismic events also include a sequence of earthquakes which occurred in 1967 along the Red Sea rift system at a distance of about 150 km to the south west of Jeddah [5] . Recently, EI-Isa et ale [6] reported that about 500 local earthquakes with magnitudes less than 4.85, occurred in the Gulf of Aqaba area during the period from January 21 to April 20, 1983. Merghelani [7] has also reported that a high level of micro-earthquake activity was detected near the border of the Red Sea and near the transition from oceanic to continental crust.
1.2. Seismicity of Gulf of Aqaba
The Gulf of Aqaba is an elongated basin (~180 × 20 km) with depths reaching 1850 m. It represents the southern
![]()
Figure 1. Earthquake intensity map for Western Region of Saudi Arabia, return period = 100 year.
segment of the Dead Sea Transform (DST), which is one of the largest transform fault zones in the world. The opening of Gulf of Aqaba is thought to have originated from the relative displacement of the African and Arabian Plates. According to historical and recent earthquake records, it is seismically active [8] , as it is shown in Figure 2.
The Dead Sea transform fault borders the Arabian plate in the west and has experienced approximately 107 km of left-lateral displacement since the mid-Miocene, which translates into roughly 6 - 10 mm/yr of slip on the fault [10] , as it is shown in Figure 3.
The Gulf of Aqaba is east of the Sinai Peninsula and west of the Arabian Peninsula. With the Gulf of Suez to the west, it extends from the northern portion of the Red Sea. It reaches a maximum depth of 1850 m in its central area: The Gulf of Suez is significantly wider but less than 100 m deep. The gulf measures 24 kilometers (15 mi) at its widest point and stretches some 160 kilometers (99 mi) north from the Straits of Tiran. Like the coastal waters of the Red Sea, the gulf is one of the world's premier sites for diving. The area is especially rich in coral and other marine biodiversity and has accidental shipwrecks and vessels deliberately sunk in an effort to provide a habitat for marine organisms and bolster the local dive tourism industry. At this northern end of the gulf are important cities: Taba in Egypt and Aqaba in Jordan. They are strategically important commercial ports and popular resorts for tourists seeking to enjoy the warm climate. Further south, Haql is the largest Saudi Arabian city on the gulf. On Sinai, Sharm el-Sheikh and Dahab are the major centers. The largest population center is Aqaba, with a population of 108,000 (2009) [12] .
Figure 4 shows the position of Gulf of Aqaba and the surrounding area relative to the map of the Kingdom of Saudi Arabia.
2. Literature Review
When considering the earthquake, we have to answer the four questions: Where? How often? How big? And When? The goal of the earthquake prediction is to give warning of potentially damaging earthquakes early enough to allow appropriate response to the disaster, enabling people to minimize loss of life and property [14] . Many studies have been presented to develop reliable estimates, of probability, magnitude and recurrence relations given the large pattern of earthquake occurrence. The primary advantage of probabilistic seismic hazard
![]()
Figure 2. Arabian plate boundaries adapted from Johnson and Stern, 2010 [9] .
![]()
Figure 3. Gulf of Aqaba-Dead Sea transform fault [11] .
![]()
Figure 4. Gulf of Aqaba and surrounding area [13] .
analysis (PSHA) is that it integrates over all seismicity: temporal and spatial along with ground motions to calculate a combined probability of exceedance, which incorporates the relative frequencies of occurrence of different earthquakes and ground-motion characteristics. Practically in any earthquake catalogue the quality of different parts (periods and areas) varies significantly with respect to completeness, magnitude reliability, homogeneity and location accuracy [15] - [17] .
Statistical theory of extreme values has been used to analyze the observed extremes of any phenomena and to forecast the further extremes based on the appropriate distribution, Gumbel [18] . In earthquake engineering, this theory has been applied successfully by many researchers in the past few decades (Nordquist [19] ; Epstein [20] ; Yegulalp [21] ; Al-Abbasi [22] and Jaiswal [23] ). This theory does not require analysis of the complete record of earthquake occurrence, but uses the sequence of earthquakes constructed from the largest values of the magnitude over a set of predetermined intervals.
Abe and Suzuki [24] analyzed the seismic data from the viewpoint of science of complexity, where one of the main goals of seismology is to predict when and where the next main shock will occur after an earlier main shock. The rate of recurrence of earthquakes on a seismic source can be represented with the Gutenberg-Richter relation [25] . Kasap and Gürlen [26] studied the return periods of earthquakes. Ogata [27] investigated the statistical models for earthquake occurrences. Utsu [28] applied gamma, log-normal, Weibull and exponential distributions to describe the probability distribution of inter-occurrence time of large earthquakes in Japan. Aktaş et al. [29] , used Poisson distribution to describe the recurrence times, and estimated the expected value and variance computed for the loss of life and damaged buildings after the change point using the compound Poisson process. Bayrak et al. [30] evaluated the seismicity and earthquake hazard parameters of Turkey based on maximum regional magnitude. Öztürk et al. [31] estimated the mean return periods, the most probable magnitude in a time period of t-years, and the probability of earthquake occurrence for a given magnitude during a time span of t-years for different regions in and around Turkey. They also showed that in the specific region, the most probable earthquake magnitude in the next 100 years would be over 7.5. Bayrak et al. [32] calculated the seismicity parameters for the 24 seismic regions of Turkey according to Gumbel and Gutenberg-Richter methods and concluded that b-values obtained from the maximum likelihood approach gives better results for the tectonics of the examined area. In a study [33] , 231 earthquake data of magnitude 5 and higher, between north (39.00˚ - 42.00˚) and east (26.00˚ - 45.00˚) coordinates in Turkey from July 12, 1900 to July 25, 2011 are analyzed. In this study, the probability distribution of magnitude is attempted and the statistical models are taken to interpret the observed frequency distribution. The earthquake catalog for Iraq covering an area between latitude 39 - 50 E and longitude 29 - 50 N and containing more than thousand events for the period 1905-2000 has been compiled The statistical parameters for Gumbel’s have been estimated using both the least squares and maximum likelihood techniques. The goodness of fit is evaluated employing Kolmogorov-Smirnov test [34] .
3. Extreme Earthquake Analysis
Earthquake prediction can be considered into two types. First is the statistical prediction which is based on previous events; Data are collected from the records. Second is deterministic prediction which is made from the earthquake signs. The table at Appendix shows the data for earthquakes in Gulf of Aqaba and surrounding area representing the minimum magnitude and maximum magnitude.
Most extreme event analysis is concerned with the distribution of annual maximum or minimum values at a given site. These events are given a rank, m, starting with m = 1 for the highest value, m = 2 for the next highest and so on in descending order. Each earthquake magnitude is associated with a rank, m, with m = 1 given to the maximum magnitude over the years of record, m = 2 given to the second highest magnitude, m = 3 given to the third highest one, etc. The smallest earthquake magnitude will receive a rank equal to the number of years over which there is a record, n. Thus, the discharge with the smallest value will have m = n = 18.
There are several formulas for calculating the probability value. The Weibull formula will be used because of its ease of use. The US Geological Survey [35] , among others, also uses this formula.
According to the Weibull equation [36] , the return period or recurrence interval T (in years) is calculated using the following equation:
 (1)
(1)
where: m = event ranking (in a descending order), and n = number of events in the period of record.
The percentage probability the (annual exceedance probability) for each magnitude is calculated using the inverse of the Weibull equation as follows:
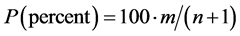 . (2)
. (2)
From Equations ((1), (2)) it is clear that P = 100/T%. For example, an earthquake equal to that of a 10-year one would have an annual exceedance probability of 1/10 = 0.1 or 10%. This would say that in any given year, the probability that an earthquake with a magnitude equal to or greater than that of a 10-year earthquake would be 0.1 or 10%. Similarly, the probability of an earthquake with a magnitude exceeding the 50 year one in any given year would be 1/50 = 0.02, or 2%. Note that such probabilities are the same for every year, but in practice, such an earthquake could occur next year, or be exceeded several times in the next 50 years.
Table 1 shows the calculations of the rank m, the probability P and the return period T for the data of the yearly maximum magnitude given in the Appendix and Figure 5 shows the location of given data in the Appendix.
![]()
Figure 5. Location of give date in the Appendix [38] .
![]()
Table 1. The rank, probability and the return period results.
4. Earthquake Parameters
4.1. Annual Exceedance Probability and Return Period
Return period or Recurrence interval is the average interval of time within which a flood of specified magnitude is expected to be equaled or exceeded at least once. 19-year earthquake is an earthquake that is expected to occur, on the average, once every 19 years, or has 5.26% chance of occurring each year.
Figure 6 is a plot of earthquake magnitude and annual exceedance probability relationship (linear scales) with the annual maximum magnitude per year on the Y axis versus the annual exceedance probability on the X axis. The X and Y axes both use linear scales.
A best-fit curve is drawn through the data points. From the best-fit curve, one can determine the earthquake magnitude associated with an earthquake with a recurrence interval of say 1.9 years, it is about 3.95 on Richter scale. This would be called the 2-year earthquake.
Similarly, the recurrence interval associated with an earthquake magnitude of magnitude of 5.08 on Richter scale is about 19 years.
The annual peak information may also be presented with a logarithmic rather than a linear scale. This is often done to make the curve appear as a straight line and also to avoid a graph that will suggest either a zero or a one-hundred percent exceedance probability. Moreover, a straight line curves are more easily allow extrapolation beyond the data extremes. Figure 7 represents the earthquake magnitude and the annual exceedance probability (log scale) relationship.
Percentage probability is determined by dividing one by the recurrence interval and multiplying by 100. For example, the probability that an earthquake magnitude will exceed the 19-year earthquake this year or any other year would be 5.26%.
Figure 8 shows the earthquake magnitude and return period relationship on linear scales. From the figure it can be noticed that the return period of an earthquake of magnitude 5.08 on Richter scale is about 19 years, and an earthquake of magnitude of 4.44 on Richter scale has a recurrence interval of about 6.33 years.
Sometimes it is suitable to add a second Y-axis to represent the return period to the first Y-axis representing the annual exceedance probability. Figure 9 shows the earthquake magnitude on the X-axis and the annual
![]()
Figure 6. Earthquake magnitude and probability relationship (linear scales).
![]()
Figure 7. Earthquake magnitude and annual exceedance probability (log scale) relationship.
![]()
Figure 8. Earthquake magnitude and return period relationship (linear scales).
exceedance probability on the first Y-axis and the return period on the second Y-axis. Both the two Y-axes use avariable log scale so the relationship appears as a semi-parallel line, this will allow for easier findings.
From Figure 10, as the earthquake magnitude increased more than 3.3 on Richter scale the returned period will have increased and the probability will have decreased, this relation can be determined by the increment of the gap between the probability and return period lines.
![]()
Figure 9. Earthquake magnitude, probability and return period relationship.
![]()
Figure 10. Earthquake probability for some earthquake magnitudes in a time span period.
4.2. The Probability during a Time Period
Theprobabilityofacertain-magnitudeearthquakeoccurringduringanyperiod t can be calculated using the following equation:
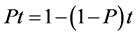 (3)
(3)
where P is the probability of occurrence over the entire time period, t, and P is the probability of occurrence in any year.
It is worth to apply equation (3) for earthquakes of highest magnitudes which represent the most dangerous events in the study. The equation is applied for earthquakes of magnitudes 5.08, 4.65 and 4.44 Richter scale of probabilities of 5.26%, 10.52% and 15.78% respectively. The result is depicted in Figure 11 for earthquakes of magnitudes: 5.08 Richter scale (P = 5.26%), 4.65 Richter scale (P = 10.52%) and 4.44 Richter scale (P = 15.78%).
A homeowner considering the costs of reinforcing a house against earthquakes will want to know how the risk varies during an average mortgage span of 5 years. Figure 11 shows the earthquake probability and earthquake magnitudes in a time span of 5 years. An earthquake of magnitude of 4.44 on Richter scale for example, has a 57.65% probability of occurrence but, if the earthquake of magnitude 5.08 on Richter scale is chosen, the probability drops to 23.69%.
In addition, from Figure 11, any earthquake of magnitude less than 3.56 on Richter scale has a 100% probability of occurrence.
5. Conclusions and Points for Future Researches
5.1. Conclusions
Earthquake is an unavoidable natural disaster for the region. Hence, to take precautions for the future by utilizing the past experiences is very substantial. This can be a kind of a proposition to the higher authorities to have an open eye to this particular region.
In this study, the statistical frequency analyses are applied to the recorded annual maximum earthquake magnitudes for Gulf of Aqaba since 1999.
![]()
Figure 11. Earthquake probability and earthquake magnitudes in a time span of 5 years.
The earthquake hazard parameters are estimated, these are: the mean return periods (recurrence intervals), the frequency, the probability of earthquake occurrence (annual exceedance probability) for a given magnitude during any year, and the probability of earthquake occurrence for a given magnitude during a time span of t-years with a stress on a 18-year period. The Weibull equation is applied to estimate the return period, while the inverse of the Weibull equation is used to calculate the probability of occurrence.
The relation between magnitude and frequency and between magnitude and return period is represented as a curve in a linear scale graph and as a straight line on a logarithmic scale and variable scale graphs to facilitate the findings. The results lead to a general conclusion that Gulf of Aqaba is considered as a high seismic area and the region is exposed to earthquakes with strength ranging of 5 or more on the Richter scale with a high probability. The maximum magnitude is 5.08 with a return period of 19 years and probability of about 5.26%.
5.2. Points for Future Researches
Points for future researches can be summarized as follows:
・ To study in details the period before 1999 where it is included a recorded earthquake with magnitude 7.3 Richter scale on 1995.
・ To use other methods for evaluation of earthquake parameters and compare the obtained results.
・ To estimate earthquake hazard parameters for regions around Gulf of Aqaba.
・ To estimate hazard parameters for other events like: floods, subsidence, volcanic eruptions and severe storms in different regions around Gulf of Aqaba.
・ To draw a seismic map for Gulf of Aqaba region and for other regions around it.
Acknowledgements
We would like to present our appreciation to Professor Amar Ameen, Dean of the Faculty of Earth Sciences, King Abdulaziz University, Saudi Arabia and Assistant Professor Abdul-elah Bahabri, Engineering and Environmental Geology Department, King Abdulaziz University for their appreciated help.
In addition, special tanks to Hani Zahran, Directing Manager, National Center for earthquakes and volcanoes, Geological Survey Authority, Saudi Arabia, for providing all seismic reading of Gulf of Aqaba, which used in this paper.
Appendix
Data for the earthquakes in the Gulf of Aqaba from May, 1999 to Feb, 2016 [37] .
NOTES
![]()
*Corresponding author.