Received 18 March 2016; accepted 8 May 2016; published 11 May 2016

1. Introduction
The water pipeline plays an important role in the daily life of residents. The purpose of water pipelines is to transport surface water and/or ground water from one place to another. Failures of those pipes are inevitable in the facility management. Such burst pipes in the water system are one of the most common issues at a resident’s home as well as in the public system. There are multiple causes for such failures, including pipe age, pipe material, soil erosion, corrosion, human factors, cold weather and hydraulic pressure. The impacts of water pipeline failure can be very devastating to the surroundings. For example, a failure on the water main at home creates damage to surrounding properties, leaves residents without water supply for days. A pipe burst on the main system may impact the entire area of a city and cause huge trouble for residents.
Depending on the maintenance efforts, the rates of such failures vary substantially from municipality to municipality. A well maintained water pipeline system may have a very low failure rate. Those failures are usually considered random behavior of the system’s performance. On the contrary, a pipeline that is impacted by various issues, such as old ages, unsteady pressure issues, may have a relatively high failure rate. In other words, the arrival rates of such pipeline failure are a great indictor of the system’s condition. The change of such rate provides valuable information to decision makers in terms of maintenance effort investment.
This paper analyzes the water pipeline failure data from a municipality. Data consisted all water failures reported by residents in recent years (from 2011 to 2014). Those events are usually regarded as random behavior, which is featured with a Poisson process. Such homogeneous assumption may not be justified in all cases. This study investigates whether the arrival of water pipeline failures can be modeled with a Poisson process. The reliability models are also applied to evaluate the asset safety. The results will affect the facility management adversely.
Research related to water pipeline has been conducted extensively in the past years. Literature can be grouped into 3 categories. The first category is the analysis of pipe failures and hydraulic performance. For example, Schmitt et al. proposed a numerical model to simulate the propagation of pressure waves in water networks [1] . This method investigates the defect geometry effects, such as semi-spherical and semi-elliptical defects. Moglia et al. developed a method to support pipeline renewal prioritization [2] . The method involves the assessment of various activities, including pipeline replacement and pressure reduction. By using the water pipe breaks as an indicator of the structural sate of a network, Pelletier et al. applied the survival analysis on three case studies to evaluate the reliability of the water system [3] . Similar reliability studies have also been conducted in sewer pipeline [4] [5] . Methods proposed in those studies can also be used in the analysis of water pipeline failures. In terms of hydraulic performance evaluation, flows are usually modeled using simulations [6] - [9] .
The second category is the condition prediction of water main. For example, Sadiq et al. used a fuzzy-based method to evaluate the soil corrosivity in the deteriorating of water mains [10] . Two case studies are used to demonstrate the method. In general, there are not many publications related to the water main pipeline. However, relevant studies upon the storm water pipeline and sewer pipeline has been explored in literature. For example, Micevski et al. uses the Markov chains model to predict the storm water pipe deterioration [11] . Jinand Mukherjee proposed methods estimate the transition probabilities in a Markov chains model application [12] . They further evaluated the sensitivity of the Markovian model [13] .
The third category is the life cycle analysis for the purpose of sustainable management of pipeline systems. For example, Piratla et al. estimated the CO2 emissions from the life cycle of a potable water pipeline project [14] . By dividing the life cycle into several phases, emissions from each phase are quantified in the study. Filionet cal. conducted life cycle energy analysis of a water distribution system [15] . Jinand Mukherjee proposed a stochastic approach in the life cycle analysis of pipeline system [16] . The method can also be used to evaluate theanalysis of water pipeline.
This study falls into the first category. By focusing on the water pipeline breaks, this research aims to explore the arrival pattern of such failures. Method proposed by Jin and Mukherjee are used in this study [4] . The 2-sample KS test is adopted to check the similarity between the incomplete data set and the entire data set. The reliability models are also adopted to evaluate the system’s performance. The long term goal is to integrate those individual little models into a macro model to support decision making in co-dependent infrastructure systems [17] .
2. Methodology
The methodology is constructed and presented based on the data characteristics. The data obtained are water pipeline breaks collected between April 2011 and Dec. 2014. The data set from 2011 is not complete. Two analysis steps are conducted in this study.
Considering that the data in 2011 is not complete, the first step is to check whether this data set is similar to the entire data set. To achieve such goal, the two-sample Kolmogorov-Smirnov (KS) test was performed to investigate if there are any significant differences between the data sets. The KS is chosen due to its un-sensitivity to the underlying distribution of the data [4] . The null and alternative hypothesis is:
H0: The two data sets have a common distribution
H1: The two data sets do not have a common distribution
Significant level: 0.05
The second step is the reliability analysis. Existing reliability models, such as Crow’s model [18] and Cox- lewis’ mode [19] use the Weibull distribution to fit the “time to failure” data. Such Weibull distribution has been used to characterize time series data, especially when the arrival rates are not constant. Specifically, the standard Weibull distribution has the density function
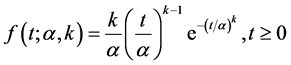 (1)
(1)
and distribution function
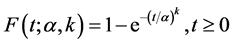 (2)
(2)
In those functions, k is the shape parameter, α is the scale parameter. When k > 1, it indicates that the arrival rate increases with time. When k < 1, it means the arrival rate decreases with time. When k = 1, the Weibull distribution is reduced into an exponential distribution. The arrival rate is constant, therefore, it is a Poisson process.
By introducing the location parameter γ, the 2-parameter Weibull can be extended into a 3-parameter Weibull distribution. The location parameter is used to describe the shift in the distribution. The density and distribution functions become
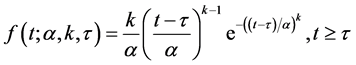 (3)
(3)
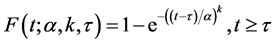 (4)
(4)
The “time to failure” data is used in the Weibull distribution fitting. In order to obtain the data, it is assumed that the starting time is the first day of the data’s duration. For example, for the 2012 data, the starting time is the first day of 2012. For the entire data set, the starting point would be the first day of 2011. The Weibull fitting is performed using the Minitab tool. Minitab uses the Anderson-Darling (AD) statistics in such reliability analysis.
3. Results and Discussions
The KS test was performed in Minitab. Figure 1 displays the 2 sample KS test result. As shown in Table 1, The test statistics is less than the critical value. Therefore, the null hypothesis is accepted. The 2011 data set has no significant difference to the entire data set. In the following analysis, the 2011 data is also included.
Figures 2-5 display analysis results for the annual data set. In general, the 2-parameter Weibull distribution generates fine fittings for those data sets. The shape parameter for the annual data sets is all a little greater than 1, indicating there is an slightly increased arrival rate of those failures. The shape parameter for the 2011 data is 4.28, which is way above the threshold value 1. Since the data fit the Weibull distribution very well, it is safe to conclude that the water break arrivals have an increased rate during this year. However, considering missing data in 2011, such result might not be used to characterize the failure rate within this year. As a matter of fact, the missing data also have an impact on the entire data analysis.
In terms of the entire data set, as shown in Figure 6 and Figure 7, the 2-parameter Weibull generates a fine fitting, while 3-parameter improves the fitting a little bit. The shape parameter is well greater than 1, indicating there is an increased water pipeline break during those years. However, the entire data set contains the 2011 data that is known to be incomplete. To eliminate the impact of the missing data in 2011, data from 2012 to 2014 are combined to create a new data set. The same analysis was conducted upon the data. The Weibull fitting is shown in Figure 8. The fitting is satisfactory with a shape parameter 1.03. The 3-parameter Weibull improves the fitting a little better with a lower AD value. As shown in Figure 9, the shape parameter is 1.10. Therefore, the arrival of water break has a slightly increasing rate during 2012 and 2014 in Table 2.
![]()
Figure 2. Weibull distribution fitting for 2011 data.
![]()
Figure 3. Weibull distribution fitting for 2012 data.
![]()
Figure 4. Weibull distribution fitting for 2013 data.
![]()
Figure 5. Weibull distribution fitting for 2014 data.
![]()
Figure 6. 2-Parameter Weibull distribution fitting for the entire data.
![]()
Figure 7. 3-Parameter Weibull distribution fitting for the entire data.
![]()
Figure 8. 2-Parameter Weibull distribution fitting for the 2011-2014 data.
![]()
Figure 9. 3-Parameter Weibull distribution fitting for the 2011-2014 data.
![]()
Table 2. Parameters of the Weibull fitting for each data set.
4. Conclusion
In the water pipeline management, water breaks are common issues which can be used as an indicator of the system’s performance. Those failures sometimes are regarded random behavior. In some cases, such assumption cannot be justified. This paper explores the arrival pattern of water pipeline breaks. Two main issues are addressed. The first problem is the handling of incomplete data set. The 2-sample KS test is adopted to verify the similarities between data sets without indicating any underlying distribution. The reliability analysis is then conducted on all data. The results show that for the annual data set, a slightly increased rate is noticed for the break arrivals. For the entire data set, the 3-parameter Weibull generates a shape parameter well greater than 1, indicating an increased arrival rate. To eliminate the impacts of incomplete 2011 data set, data from 2012 to 2014 were treated as a new set. The analysis reveals that the shape parameter is a little greater than 1. Therefore, there is a slightly increased failure rate over this duration, which is consistent with the conclusions obtained from the annual data set analysis. In summary, results from this paper provide information to the water pipeline managers. In this specific case, more efforts are needed to lower the frequency of the water burst issues.