On the Origin of Charge-Asymmetric Matter. II. Localized Dirac Waveforms

Alexander Makhlin

Rapid Research Inc., Southfield, MI, USA.

DOI: 10.4236/jmp.2016.77066                

Abstract

This paper continues the author’s work [1], where a new framework of the matter-induced physical geometry was built and an intrinsic nonlinearity of the Dirac equation was discovered. Here, the nonlinear Dirac equation is solved and the localized configurations are found analytically. Of the two possible types of the potentially stationary localized configurations of the Dirac field, only one is stable with respect to the action of an external field and it corresponds to a positive charge. A connection with the global charge asymmetry of matter in the Universe and with the recently observed excess of the cosmic positrons is discussed.

Keywords

Nonlinear Dirac Field, Localization, Cosmological Charge Asymmetry

Received 25 February 2016; accepted 25 April 2016; published 28 April 2016

1. Introduction

This paper continues the author’s study of the long-standing question of how the physical Dirac field of a real matter becomes a finite-sized particle, and it is approached here as a practical problem. The problem is posed and solved in a new framework of the matter-induced affine geometry [1] , which deduces the geometric relations in the space-time continuum from the dynamic properties of the Dirac field. The intuitive argument of a possible auto-localization of the Dirac field followed from an observation [1] that the local time flows slower at higher invariant density, and then from the wave nature of the Dirac equation. Its further consequence must be the (well-known but not clearly understood) charge asymmetry of the observed localized matter. In the present work, these qualitative expectations are confirmed by explicit calculations.

The earlier developed [1] mathematical background for the present work is based on the following ideas and results. It is observed that if at a point in spacetime continuum (the principal differentiable manifold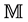) a physical Dirac field is defined, then the latter determines the tetrad of Dirac currents. These are linearly in- dependent and Lorentz-orthogonal and can serve as local algebraic basis for any four-dimensional vector space, including the infinitesimal displacements in coordinate space.

The Dirac currents are employed as the Cartan’s moving frame in spacetime which, in its turn, results in the technique of covariant derivatives for the vector and spinor fields. The physics is naturally brought into this mathematical picture by the equations of motion of the Dirac field, which made an artificial tangent (pseudo) Euclidean space unnecessary. Differential identities derived from equations of motion fully determine all the components of the matter-induced affine connection (the Ricci coefficients of rotation of the tetrad) in 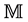and without resorting to a particular coordinate system. Thus determined connections completely define an affine geometry (endowed with the connection but with no metric). Thus defined connection depends on the Dirac field which makes the Dirac equation nonlinear.

With known connections, it became possible to find the coordinate lines and coordinate surfaces of the matter-induced affine geometry, which have a clear physical meaning and quite high degree of symmetry. The congruence of lines of the timelike vector current appeared to be normal, thus determining the family of the hypersurfaces of the constant world time. The lines of the spacelike axial current appeared to be straight and their congruence normal. They define the surfaces of the constant distance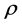. The two-dimensional surfaces of constant 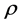at a given time were proved to be just spherical surfaces.

Below, the inevitable localization of the Dirac field into particles observed in real world, but not explained by any theory so far, is confirmed by the analytic solutions of the nonlinear Dirac equation in one-body appro- ximation. One of the solutions has maximum near its center and is clearly associated with a stable localized positive charge. Another one has minimum and is sought to be an intrinsically unstable negative charge, which can be only weakly localized by an external field.

The content of the paper is organized as follows. In Section 2 we use the previously developed [1] tools of the matter-induced affine geometry to write down the Dirac equation in its most general coordinate-independent form. Then, in Section 3 we derive the formulae that connect the Dirac matrices in the principal manifold 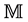and in arithmetic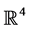. In Sections 4 and 5, the Dirac equation is written down in a mixed representation, with derivatives in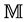, and coordinates and Dirac matrices in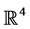. This representation is well suited for finding the analytic solution. These solutions are found in Section 6 and their stability is discussed in Section 7. The con- ceptual questions of the charge-asymmetric real world are briefly discussed in the Summary.

2. The Framework

In the first part of this work we explored differential identities for the four Dirac currents, vector current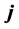, axial current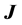, and two “ charged currents”, and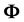. Using them, we found all components of the affine connection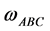, as well as connection of the Dirac field in principal manifold,

(2.1)

The connection (2.1) determines the covariant derivative of the Dirac field and it enters the Dirac equation as,

(2.2)

The nonzero elements of the in the tetrad basis of the normalized Dirac currents are as follows,

(2.3)

where is the derivative of the invariant density in the direction of the axial current and it has an algebraic representation via the pseudoscalar density. These formulae assume that

for the right-handed spatial triad with, and the naturally out-

ward directed axial current, i.e. [c.f Equations (A.9), (A.10)]. When the latter is

directed inward, but we still wish to point outward, then we have to take, and re- place (or) in Equation (2.3)¹.

It is instructive to see how the operator carries out the parallel transport of the Dirac spinor in different directions. Substituting the results (2.3) into connection (2.1), it is straightforward to obtain,

(2.4)

where. The upper and lower signs in the projector (accordingly,

the sign in) correspond to the outward and inward directions of the axial current, respectively, which then determines the right- and left-oriented spatial triplets. It will be shown below, that, from the perspective of the localized solutions, this orientation is translated into the bump of the positive charge and

to the dip of the negative one, respectively, i.e.. Therefore, depending on this sign, only the

locally inward or locally outward components, or, interact with the electromagnetic potential but with the doubled coupling constant. In a sense, the charge conjugation goes together with spatial reflection. The matrix differentiate between the right and left components.

With the connection (2.4) the Dirac equation becomes a nonlinear equation and its explicit form reads as,

(2.5)

where anomalous term singles out the direction of the axial current among others even when.

This equation is valid in every connected domain where and the Dirac currents define a non- degenerate orthogonal tetrad. As anticipated, it is invariant in a most broad sense―it depends neither on choice of coordinates in nor on a tetrad system (also in) not even on a particular choice of the -matrices. The latter is always taken for granted since one can introduce a new Dirac field leaving the gamma matrices unchanged. But this trick works only for re-parameterizations in, i.e. change of the Lorentz frame or transformations between orthogonal coordinates. It cannot be employed in the principal manifold just because the Dirac field is a coordinate scalar.

Finally, Equation (2.5) is nonlinear because both the connection and the Dirac matrices in it depend on the Dirac field. The dependence of on the Dirac field is due to (2.3). The dependence of the Dirac matrices on, , is not so explicit but not less important and it cannot be avoided. Indeed, in the basis each of the currents has only one nonzero component, e.g.,

The latter cannot be achieved without an explicit dependence. Indeed, with and numerical matrices the current will have all components. Obviously, this is a significant technical difficulty. However, only this dependence solves a conceptual problem of independence of the equation of motion for the physical Dirac field in on a particular choice of the tetrad and of the matrices in tangent. Therefore, we begin with the establishing rules of transformation of the 16 Dirac matrices between and.

3. Dirac Matrices in Principal Manifold M

Historically, the Dirac equation for the free field was formulated as with the aid of Hermitian Dirac matrices and, which satisfy the commutation relations,

(3.1)

Usually one assumes that;; (so that is a unit matrix) but this is not required. An apparently symmetric form of commutation relations (3.1) emerges (along with the equation,) in terms of the matrices,

(3.2)

Neither of these matrices is uniquely defined. However, if there exist two sets of the matrices, and, that satisfy (2) then, according to the Pauli’s fundamental theorem, there exists such a nonsingular S, that

(3.3)

where, is a number standing for superscript A and is the same number for superscript a.

There are sixteen linearly independent matrices, all of which are the products of 1,

2, 3 or 4 different gamma. Therefore, , which is an indisputable technical advantage.

By their definition, the matrices are not Hermitian. However, since and are Hermitian and anti-

commuting, the Hermit-conjugated -matrices are. If, by the same token,

(with Hermitian and), then, which yields,

Multiplying this by S from the left and by from the right, we find,

(3.4)

The matrix commutes with all the matrices and must be the unit matrix, viz.,

(3.5)

On the one hand, we can continue as

(3.6)

On the other hand, condition (3.5) means that, which conflicts with Equation (3.3), because matrix S is not unitary. This conflict can be avoided by adopting a slightly different agreement (that does not affect any of the common usages of the gamma-matrices). Namely, let us denote and define -matrices as and. Now we must replace both and in Equation (4) by,

so that and in compliance with

(3.3). Choosing, we have, ,.

Throughout this paper, we are only interested in a special case of the transformations (3.3) and (3.6),

(3.7)

where the transformation matrix is real and has the properties,

(3.8)

Then the commutation relations (3.1) are the same for and and S must be a solution of the matrix equation,

(3.9)

Though has a character of a Lorentz transformation, it has no infinitesimal prototype. Since , we also have a habitual. However, in the basis of matrices, the Pauli-conjugated Dirac spinor must be defined as and not as.

The set of 16 linearly independent elements of Clifford algebra comprised of various products of the - (or the -) matrices is in one-to-one correspondence with 16 Hermitian matrices, , , where, , and. The Dirac matrices, and, satisfy the same commutation relations as the Pauli matrices, , and. Finally, it is straightforward to check that the matrix (commonly known as) is an invariant of transformations (3.3),

(3.10)

Then the matrix is transformed like, so that

(3.11)

As long as, the matrices on the, being defined as, are transformed as

(3.12)

(as it should be for the spatial components of the axial current)².

4. The Nonlinear Dirac Equation, Explicitly

So far, we have been studying the general geometric properties of the Dirac field in the scope of the affine geometry and carefully avoiding any assumptions about what a solution of the Dirac equation that has these properties can be. All the previously established [1] properties of the Dirac currents belong (along with the Dirac field itself) to the principal differentiable manifold. Without resorting to any particular coordinate manifold we have established in [1] the following facts:

(i) The congruence of lines of the vector field is normal. The family of hypersurfaces, , of the constant world time is extrinsically flat; is a holonomic coordinate and it can be taken for in.

(ii) The congruence of lines of the vector field is normal and geodesic. The hypersurfaces of the constant radius have constant extrinsic curvature and the holonomic coordinate can serve as in.

(iii) The two-dimensional surfaces of constant and are just spheres, i.e. umbilical (with two equal Gauss’ curvatures) surfaces with constant mean (extrinsic) curvature. The latter is determined by the Dirac field within principal manifold and depends only on the radius. The intrinsic

(sectional) curvature, , is due to the external electro-

magnetic field. It coincides with projection of the magnetic field onto the direction of the axial current.

(iv) The two-dimensional surfaces are covered by a well-defined coordinate net formed by the stream- lines of the vector and axial currents. This net can be identically mapped between the principal manifold and the arithmetic.

These general observations can be summarized as follows. For any solution of the Dirac equation, which is not homogeneous in spatial directions, the spherical symmetry is the property of a solution, thus being a dy- namic symmetry.

In order to find a solution of the Dirac equation, one has to specify a coordinate basis in and a basis of the Dirac matrices. Here, we shall employ the numerical matrices in spinor representation (A.7) and asso- ciate them with a tetrad. Then, , while the derivatives will stay in the basis, which is associated with coordinate surfaces determined in the principal manifold. In this mixed representation, Dirac equation reads as

(4.1)

The operators, which are copied from Equation (2.5), are as follows,

(4.2)

where differentiate between the right and left components and it stands for for and for for The coordinate net formed by the integral lines of the tetrad vectors and that covers the two-dimensional surface in is holonomic and the vectors in can be chosen tangent to this surface. In order for the other two tetrad vectors, and, to be normal to this surface, it is necessary that the components. Just by inspection of Equations (A.9), we see that this is possible only when either or. In both cases, as seen from Equations (A.10), we have. In other words, the spacetime with the matter-induced anholonomic basis can be viewed as a direct product of the two-dimensional subspaces,. This is sufficient to treat the up- and down-polarizations separately,

(4.3)

Having only or components, the states and cannot bear quantum numbers of an

angular momentum. For the up-polarized, we have,. In this

case [C.f. (A.9)-(A.11)], and the matrix in the l.h.s. of Equation (4.1) simplifies to

Accordingly, system (4.1) for becomes

(4.4)

For the down-polarized, we have,. Here, and the elements of the matrix in the l.h.s. of Equation (4.1) become,

Now, the system (4.1) reads as

(4.5)

Remembering about the sign due to, we obtain the following formulae for all the differential operators involved,

(4.6)

In Equations (4.4) and (4.5), the operator acts only on and while only on and.

5. Solutions of the Nonlinear Equations

So far we were expanding the vector of spacetime displacement in terms of the basis of the tetrad determined by the Dirac currents. But the true physical variables are the world time and the distance. They are holonomic coordinates, because and are the total diffe- rentials of the independent coordinates,

(5.1)

Here, the upper sign is for the, where. The lower sign is for, where and the axial current is directed inward. The world time and the radial variable, being defined as invariants in, can immediately be used in arithmetic.

5.1. Reduction to the Physical Variables

At the points where and (in general, a 2-d surface) the relation between spatial components, , is an algebraic identity. For the axial current directed outward, i.e., we take, and, so that. In this case, we change the variables in Equation (4.4) as follows,

(5.2)

Adopting the physical variables (5.2) in Equations (4.4) we obtain the equations that eventually must be

solved. In these equations, according to (4.6), there is an operator

. Since for, a simple calculation with yields the system,

(5.3)

where. For the axial current directed inward, in order to preserve an intuitive physical under- standing of a distance from an object, we want be directed outward. Then the triplet will be left-handed. We have to take, , and in order for the vector product

to represent the external normal and the triplet to be right-handed. This results

in the interchange of the tetrad indices in Equations (2.3), or, equivalently, in the change of the sign of the tetrad components of the vector potential,. Thus, the string of the change of variables becomes

(5.4)

Note, that in the course of the change of variables outlined above, the sign of the has been changed twice. Now, using the physical variables (5.4) in Equations (4.5) we arrive at a similar system,

(5.5)

where. The difference between and is seen right in the equations of motion. The tetrad components of an external field along holonomic coordinates, , affect only -mode. The associated with the non-holonomic coordinates angular components are assembled as the ladder operators and affect pushing it up to the state. This difference between the last two equations of systems (5.3) and (5.5) points to a generic instability of the -mode³. It is discussed in Section 7.

5.2. Reduction to the Real-Valued Functions

As the last step before solving systems (5.3) and (5.5) we split real and imaginary parts of the first two equations of these systems and reduce equations to a form convenient for finding the solutions. For the mode the result reads as

(5.6)

For the mode the result is somewhat different,

(5.7)

The phases and are affected in by the right and left lightlike components of the vector potential, respectively, but with the coupling constant. Conversely, the phases and of the are not affected at all.

Next, adding and subtracting Equations (5.6.a′) and (5.6.b′) and recalling that we find that

(5.8)

where and. Repeating the same for the mode we obtain,

(5.9)

where and. Equations (5.8.d) and (5.9.d) are easily obtained from Equations (5.3.c,d) and (5.5.c,d) because none of the amplitudes and and of the phase differences depend on the angular variables S^[1] and S^[2]. We postpone discussion of the Equations (5.3.c,d) and (5.5.c,d), which are responsible for the stability or instability of the solutions, till Section 7.

Before looking for the stationary modes of the nonlinear Dirac equation we are going to learn whether they can emerge as asymptotic configurations at of a transient process that can begin from an arbitrary per- turbation or are they ad hoc constructed isolated solutions. By adding and subtracting Equations (5.6.a,b), with the l.h.s. reduced to the logarithmic derivatives, and some simple algebra we obtain

(5.10)

where. Excluding from these two equations the, one finds a first-order wave

equation, , with the wave velocity. Because, the

“propagation” of stops at. Since depends only on, both Equations (5.10) are easily integrated,

(5.11)

where the constants of integration and are arbitrary functions of only one argument. Since (and then), we find that at the asymptotic world time the coefficients in front of in Equations (5.8.a) and (5.8.c) become 2 and 0, respectively. Assuming further that (no external field), we find that and thus. Now, is the only potentially -dependent term in Equation (5.8.a); then it cannot depend on. Therefore, the only option is , , and it immediately follows that (which is an evidence that the particle is at rest!). Equations (5.11) are compatible only in the limit of since they imply; a transient process naturally requires that. Similar results are true for the mode.

6. Stationary Solutions

Being interested here only in stationary states we assume a trivial dependence of the phases of Dirac field components on, , and replace, , , throughout this section. Then, and. Taking further the coupling constant, which is, in fact, equivalent to a one-body approximation, we end up with an autonomous system of two ODEs for two unknown functions (the amplitude and the phase difference) of the natural parameter (and not the affine parameter s!) along the radial geodesic lines.

6.1. Localized Solution for the y_u-Mode of the Dirac Field

In the stationary case, Equations (5.8) for the -mode with the axial current directed outward, read as

(6.1)

where. The characteristic equation for this system,

(6.2)

is easily solved in terms of. Then, , and

(6.3)

is the first integral of system (1) depending on one, yet undetermined, constant C.

1. General (periodic) solution. Solving Equation (6.3) for, and taking into account two possible signs of C, one can rewrite Equation (1a) as

(6.4)

Thus, the dependence in the cases and is given by the quadratures [2] ,

(6.5)

(6.6)

where and is the incomplete elliptic integral of the first kind⁴,

(6.7)

Its inverse is a well-known Jacobi’s amplitude function,. Leaving aside for a while the case of, we readily find that

(6.8)

where,. Now Equation (6.1b) becomes,

(6.9)

and, since [2] , the latter equation is readily integrated,

(6.10)

In the second case of we would have

(6.11)

The Jacobi’s elliptic functions, and are known to be double-periodic functions of their argument. While periodic behavior of the phase cannot a priori be excluded, perio- dicity in radial direction is impossible for the invariant density, simply because it would conflict with the physical localization.

2. Localized (aperiodic) solution. There is, however, a special case when the module of the elliptic function and the periodicity disappears (the period becomes infinite). For the Equation (6.10), this means that so that (as well as and). For the Equation (6.11) the same would mean, which is impossible, since, by definition. Hence, the case of must be dropped from further consideration.

The constant C of integration in the Equation (6.3) is now uniquely determined as, and the equation of characteristics of system (6.1) becomes

(6.12)

Since the Jacobi’s elliptic functions with module are elementary functions, it is much easier to return to the original system (6.1) and the characteristic equation (6.12) with, using the latter as a constraint. After using the constraint (with the signs to be determined later), , the system (6.1) simplifies to

(6.13)

and its first equation is readily integrated to first, and then yields

(6.14)

When, we have, which is possible only when. We also obtain the anti- cipated and, i.e.. Returning the result of integration into Equations (6.12) and (6.13b), we simplify the latter to

(6.15)

In order for this solution to be interpreted as an isolated particle at rest, we must require that. Thus the solution

(6.16)

is the mode with the negative energy with respect to the vacuum level zero attributed to. Finally, in natural units,

(6.17)

This result also follows from Equation (6.9), since. We can take the radius of the spherical surface, where reaches its maximum (the inflection point) for the size of the particle. Here, , and, consequently, ,. Therefore (in natural units),

as it was previously contemplated. At the radius, also as expected, the phase is. Indeed, and,. The peak amplitude.

6.2. Dirac Field in y_d-Mode

We expect that in real world the mode with the axial current looking inward will be unstable and not similar, even qualitatively, to the mode. However, it is instructive to repeat the previous steps and consider only Equations (5.7) leaving aside Equations (5.5.c,d). Then most of the analysis remains the same and only Equations (6.1) and (6.12)-(6.16) are modified. Equations (6.1) now read as

(6.18)

and the change of the sign of and of the slope does not affect the characteristic equation (6.3) except that we must replace in it. Then the cases C > 0 and C < 0 must be swapped in Equations (6.4)-(6.11) with the conclusion that constant C must be determined as, and Equation (6.3) of characteristics of system (6.18) reads as

(6.19)

After using the constraint, , the system (6.18) becomes,

(6.20)

and its first equation is readily integrated as

(6.21)

Acting as previously, we simplify the constrain and Equation (6.20.b) to

(6.22)

where the second equation is identical to (6.18.b) and is a consequence of the first one. When, we have, which is possible only when. Here, the condition of a particle at rest requires that. We also obtain the anticipated and, i.e.. Thus the solution (in natural units)

(6.23)

can be interpreted as an isolated particle at rest with the positive energy, which is 2m higher than that for the similar localized static -mode. Here, once again,. If the auto-localization is a real process it must favor localization not of that has a dip, but the bump of. This is also a hint that an ad hoc created can be unstable (as it is in Nature). We elaborate on it in the last section.

Finally, for the mode with a dip of the invariant density in its interior, the invariant density reaches its theoretical minimum, , at the inflection point ⁵. At this point we have, i.e.. Inside this radius the density R, as formally defined by (6.23), becomes negative, which is impossible. This can be a yet another indication that an isolated localized negative charge is unstable (at least in the absence of external field or of stable third bodies nearby). In other words, even being localized, it most likely is “an agile shallow deepening on a hill”. Indeed, in real world of a stable matter, all electrons are light and only weakly localized around atomic nuclei, so that normal matter is charge-neutral. The heavy inward-polarized particles (e.g., antiprotons) are found only rarely and they would not be detected without abundant normal matter nearby. These probably are “deep holes on a high hill”. Verification of this hypothesis is not a one-body problem and is beyond the scope of this work.

7. Stability and an Effective Lagrangian

The two exact solutions of the Dirac equation in one-body approximation, given by Equations (6.13)-(6.16) for the modes, and by Equations (6.21)-(6.23) for the mode, seem to be very similar to each other except that has a bump and has a dip of the invariant density near the center. According to the initial hypothesis, they correspond to positive and negative charges, respectively. The primary guess was [1, 2] that the former must be localized better and (if being unstable) live longer than the later, solely because the proper time in their interior flows the slower, the higher the invariant density is. Beyond the one-body approximation, the difference between these solutions is encoded mainly in the last two equations of the system (5.3) for and (5.5) for. In the case of they do not depend on the external field, while in the case of they do. Furthermore, the tetrad components in Equations (5.5.c,d) oscillate with time as and can cause a transition from to.

The field in the Dirac equation is an external field. Remarkably, whatever this field is, the Dirac field determines world time across every auto-localized object. In a sense, all solutions of Equations (5.3) and (5.5) with the energy are the static solutions. But it is well-known that not all static solutions are stable. Solutions (6.16) and (6.23) obtained in absence of an external field are both truly static since there is nothing in Equations (6.1) and (6.18) that could have trigger instability. To investigate the effects of instability one must return to Equations (5.5.c,d) and also to Equations (5.8) and (5.9), which also account for the external field and dynamics of the sums of phases,. The problem has two different aspects, viz., formation of a perturbation and its decay.

Below, we try to specify both aspects and speculate regarding possible approaches/tools. The following ter- minology seems most appropriate for the discussion. Let us consider the components of and as the

wave functions of the initial state and denote them as. Next, let us contract Dirac equation with the

Hermit conjugated wave function of a “final state”, and consider as “ transition amplitudes”.

7.1. Creation of Perturbations in Dirac Vacuum

The problem of what may trigger the initial (and almost necessarily unstable) configuration is the most subtle one. Classically, one has to start with arbitrary initial field and a plausible external field (i.g., of the cosmic microwave background). In quasi-static regime, the interaction of reasonably well defined initial states with the lightlike components of the vector potential is not distractive, since Equations (5.3.a,b) can contribute only to diagonal (with respect to the spin) matrix elements,

(7.1)

These are not the transitions between up- and down-states. Regardless how weak this interaction is, it takes place in enormous space and for astronomical times. It can collapse to a solitary excitation just because such excitations exist. This mechanism can be considered as a potential source of the cosmic positron excess (for an extensive review see Ref. [3] ). Furthermore, in Equations (5.3.c,d), which could have trigger transition from up- to down-states, there is no interaction terms at all. Thus, solution (6.17) of Equations (5.3), which is associated with a positive charge, is expected to be stable.

7.2. Decay of an Initial Perturbation

If an initial finite waveform is given, a reasonable theory must predict its decay into stable solitary configu- rations. Equations (5.5.c,d) (unlike (5.3.c,d)) prompt the interaction

(7.2)

that affects stability of the localized inward-polarized state. In these formulae, and are the com- ponents of vector potential with respect to a judiciously chosen basis on the surface mapped onto. The transition from unstable mode to the stable one is due to the charged Dirac currents that naturally oscillate as, and this transition can be triggered by almost any external electromagnetic field. The latter can be random or regular and originate, e.g., from the cosmic background. Possibly, they can even stabilize the mode for a long time. This could explain the difference between an apparently stable particle in a storage ring and a visibly unstable particle in the natural world.

7.3. Similarity to Magnetic Resonance?

The matrix elements (7.2) are intimately connected with the dynamics of the spin 1/2 in magnetic field, where quantum and classical equations of motion coincide. Indeed, the sectional curvature⁶ of the spherical surface (the curvature of the lines of the charged currents and),

(7.3)

is totally due to the projection of the external magnetic field onto radial direction of the axial current. If such a projection is not zero, it will cause flip of the spin polarization into the outward direction of the stable - mode.

7.4. An Effective Lagrangian

More accurate approach that would allow one to go beyond the lowest order approximation can probably be based on the so-called effective Lagrangian, , with the operator of Equation (2) in brackets. The terms depending on in it can be viewed as the interaction with the outside sources. Retaining the interaction term (), actually, leads beyond the one-body approximation. Below, solely for the purpose of stability analysis, we add the alien up- and/or down-components as a perturbation. The state is supposed to be stable if the alien components dissipate due to the interaction. It will be genuinely unstable if the interaction enforces dissipation of the native components. We continue to dub the configurations with as (with native u and an admixture of alien d). Those with are dubbed as (with native d and alien u).

Let us look at the terms associated with the charged currents and and consider the matrix element,

(7.4)

between the configurations and. Here, stands for when the triplet forms the right-handed system, and for when this triplet is left-handed. As an illustration, consider a particular term assuming native and alien; then is

(7.5)

Here, is the ladder (spin-flip) operator for the projection of spin 1/2 onto the positive direction of the right-hand oriented triplet. Let us recall that are the projection operators onto the up-/down-components of the Dirac spinor. In detail, the action of the operator is as follows. The ladder operator eliminates the native components and (acting on as) and replaces them with the alien and, producing. Since, this can be viewed as a two-step action. Namely, the (inherited from connection (2.4)) filters out the and in their alien position, and then moves them “up”, thus filtering out the positive helicity of the native “up”- final state. In other words,. If the state was a pure up-state and had no components at all, then; this is the case of Equations (3)―the does not interact with the external. Conversely, a solitary localized state that has only is un- stable under this interaction and the charged currents will smoothen it, or even cause its decay. This reproduces the primitive analysis of Equations (7.1) and (7.2).

Since the effective Lagrangian is nonlinear, there are many open questions, which cannot be addressed com- prehensively within the scope of the present work. For example, it is not clear a priori, which of states, initial or final, should determine the nonlinear terms. These issues will be discussed separately. Of highest priority are the questions about time scales of the processes that contribute to the transition amplitudes (2) as well as about stability of the uniform distribution of the invariant density.

8. Summary

1. The method. The most intriguing discovery of this work is that Dirac field endows spacetime with a matter-induced affine geometry (MIAG), which is fully determined by a real matter. This is possible solely because the Dirac field satisfies equations of motion. Then, and only then, the geometry is independent of a particular coordinate background. Possibly, this result can look strange for mathematicians. But it should not surprise physicists, who know very well that nothing in spacetime can be measured without localized material objects. So far, the method of MIAG determined the shape of a solitary localized object as spherical dynamically and with no conjectures. The problem of signals still has to be worked out.

2. The results. The author’s conjecture [4] that there exists a generic mechanism of the Dirac field auto- localization into finite-sized positively charged Dirac particles is rigorously confirmed. The explicit solution representing such a particle is found. It possesses the following properties,

(i) A solitary Dirac field waveform in free space can be stable with respect to the interaction with an external electromagnetic field only if this waveform is formed solely by outward polarized components. The solu- tion that represents such a waveform has negative energy.

(ii) An apparently complementary inward-polarized solution with negative charge has positive energy. It cannot be stable as a strongly localized object; its instability is due to the indispensable “charged currents” and. They oscillate twice faster than stationary Dirac field,. The corresponding tetrad components of the vector potential affect only the inward polarized waveform, thus making it unstable. This “motion” is confined to within the spheres of a constant radius within a localized object⁷. Similar oscillations also show up in the theory of the Compton scattering as the t-channel transitions of electron into the negative energy states. These transitions are responsible for the classical part of the Compton cross-section (Thompson scattering).

3. The prospects. Our major perception of vacuum is absence of localized matter. This means that in the vacuum is constant, e.g.,. Since Dirac equation is a hyperbolic system, the Dirac field must ex- perience refraction towards domains where, amplifying even more, which resembles a well-known nonlinear effect of self-focusing. The opposite trend must be observed in domains where; the Dirac waves tend to escape them. This idea can be phrased more precisely as: Identification of the sign of with the sign of electric charge leads to a dynamic picture of an empirically known charge-asymmetric world in which stable positively charged elementary Dirac objects are highly localized (and presumably heavy), while negatively charged objects tend to be poorly localized (and presumably light). This mechanism of localization is generic and points to the picture that stunningly resembles the today’s world. It must be worked out in greater details with the prospect that the issue of cosmological charge asymmetry, first addressed long ago by A.D. Sakharov [5] , as well as the currently observed positron excess [3] , could be better understood.

Meanwhile, to validate our approach in cosmological context, two major questions must be answered,

(i) What (if anything) can trigger a spontaneous creation of a proton alone (without an antiproton)? This is the most formidable problem.

(ii) Let a pair be created in an energetic process and the antiproton be thoroughly isolated from a normal matter (except for the cosmic background radiation). Will it live infinitely long? If not, then how will it decay? This question does not seem unbearable⁹ and can be solved by methods developed in this one and previous author’s papers (work in progress).

Acknowledgements

I am indebted M.E. Osinovsky for his advice on subtle issues of spinor analysis and differential geometry and for critically reading the manuscript. This work is supported by the Rapid Research, Inc.

Appendix: Notation and Algebraic Conventions

All observables associated with the Dirac field are bilinear forms built with the aid of Hermitian Dirac matrices and, which satisfy the commutation relations

(A.1)

Throughout this paper, the Dirac matrices associated with a tetrad are numeric and are chosen in the spinor representation,

(A.2)

where are the Pauli matrices.

If the Dirac spinor is written down in terms of modules and phases of its components,

(A.3)

then, with the Dirac matrices (A.7), the scalars and the four Dirac currents have the following components,

(A.4)

(A.5)

(A.6)

NOTES

¹Throughout this paper, when uppercase index A of the basis, takes a particular numeric value we put it in brackets,. The lowercase indices a that are related to the tetrad are put in parentheses,.

²Then the charge-conjugated spinor becomes. In particular, . At the same time, and, ...

³Since and are the “angular” directions, it is instructive to recall that the operators are ladder operators for the angular momentum that moves eigenstate of the up. Both systems (5.3) and (5.5) contain only. While cannot be pushed further up (and is stable), the is readily pushed up to the. One can view these transitions as a manifestation of the -waveform’s “motion”. In fact, it is a flow of surrounding Dirac matter with that looks like a motion of the -dip (or void).

⁴These expressions have no practical value and will be used below for a sole purpose of proving that the modules of the elliptic integrals must equal +1 by the physics of the problem. Then, and only then is not oscillating in radial direction. This uniquely fixes the constant as and guarantee that elliptic integrals become smooth elementary functions. The limits of integration in (6.5) are tentative.

⁵In general, none of the Dirac currents vanishes at; they all become proportional to one lightlike vector that must have both up- and down-components. Then nothing can identify the surface of constant and as a two-dimensional sphere.

⁶The sectional curvature of a surface spanned by a net of the lines of the vectors and equals to the angle by which the basis is rotated after moving along an infinitesimal loop within this surface.

⁷This motion cannot be interpreted as an oscillation of a mean coordinate -- the famous Schrödinger Zitterbewegung.

⁸This is in contrast with the view of Dirac field as the representation of the Lorentz group. In that framework, the Poincaré invariance is presumed, and all states can be obtained from a single state by a sequence of the Lorentz transformations.

⁹Some theories of Grand Unification predict proton’s decay with a lifetime greater than the currently estimated age of Universe. From our perspective, only antiproton can be unstable.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Makhlin, A. (2016) Journal of Modern Physics, 7, 587-610. http://dx.doi.org/10.4236/jmp.2016.77061
[2]	Byrd, P.F. and Friedman, M.D. (1971) Handbook of Elliptic Integrals for Engineers and Scientists. 2nd Edition, Springer-Verlag, Berlin. http://dx.doi.org/10.1007/978-3-642-65138-0
[3]	Serpico, P.D. (2012) Astroparticle Physics, 39-40, 2-11. http://dx.doi.org/10.1016/j.astropartphys.2011.08.007
[4]	Makhlin, A. (2010) Localization, CP-Symmetry and Neutrino Signals of the Dirac Matter. arxiv:1005.2693 [math-ph]
[5]	Sakharov, A.D. (1967) JETP Letters, 5, 24-27.