Quantum Mechanical Path Integral in Phase Space and Class of Harmonic Oscillators with Varied Frequencies ()
Received 16 August 2015; accepted 23 February 2016; published 26 February 2016

1. Introduction
Recently, a great deal of attention has been paid to the subject of time dependent Hamiltonians. The importance of this problem in various areas of physics, quantum optics [1] , cosmology [2] , nanotechnology [3] and plasma physics [4] is the main reason for these intensive studies. The harmonic oscillator with time-dependent mass and frequency is a common problem in this area, and it is very important system, because we can find it in many physical areas. Abdalla and Colograve [5] -[7] studied this problem with a time dependent mass and constant frequency in order to describe the electromagnetic field intensities in a Fabry-Poerot cavity by applying a time dependent canonical transformation. The problem also has been treated using the time-dependent dynamical invariant by Lewis and Riesenfeld [8] . Kandekar and Lawand [9] have considered the case of exponentially varying mass with variable frequency by means of path integral method. The same problem with a constant frequency has been treated by path integral by many authors for example: Sabir and Rajagopalan [10] treated the cases of the strongly pulsating mass and a model of growing mass, the power-low suppressed harmonic oscillator [11] is also solved. In [12] the problem with an arbitrary time dependent mass and frequency is treated using space-time transformations. The same problem has been solved in [13] . Cheng [14] evaluated the propagator of a forced time dependent harmonic oscillator.
Looking through the literature one can find that an explicit expression for the propagator could not be obtained for all time varying mass-functions or frequencies because the procedure involves the solutions of non- linear differential equations. This is the reason why the literature is not reached by many exactly evaluated systems, which has many applications in physics [1] - [4] [15] [16] . Only few cases of varying mass and frequency have been solved, as mentioned above the strongly pulsating mass [7] , the exponentially time-dependent mass [17] , the power-low mass [11] and some examples are given in [18] - [20] .
In this paper we will present a way to find the propagators of the time dependent harmonic oscillators in phase space using canonical transformations and delta functional integration [21] . As an application of that we will follow by a class of time dependent harmonic oscillators with time-dependent frequencies we think and see that they have exact propagators.
2. The Harmonic Oscillator and the Propagator
Let us present the following time dependent Hamiltonian [17]
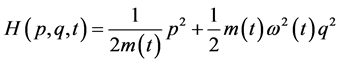 (1)
(1)
The propagator corresponds to this system can be written in the phase space as
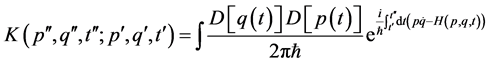 (2)
(2)
This propagator is not exactly evaluated for any arbitrary time dependent mass or frequency, because that will lead to non-linear differential equations. To deal with this system we will absorb the quadratic term of q, by taking the following transformation
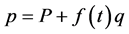 (3)
(3)
where 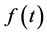 is an arbitrary function. The propagator (2) under this transformation will have the following form
is an arbitrary function. The propagator (2) under this transformation will have the following form
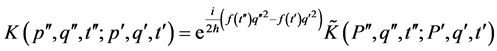 (4)
(4)
where 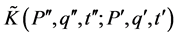 is the propagator that has the following expression
is the propagator that has the following expression
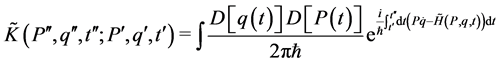 (5)
(5)
and the new Hamiltonian 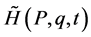 is
is
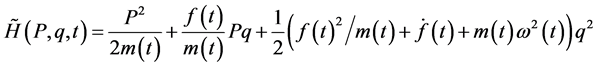 (6)
(6)
Since 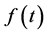 is an arbitrary function we will choose it such that the quadratic term in the new Hamiltonian disappears
is an arbitrary function we will choose it such that the quadratic term in the new Hamiltonian disappears
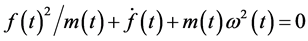 (7)
(7)
Then  will be
will be
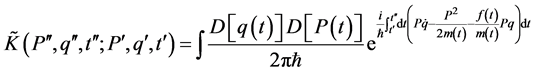 (8)
(8)
to deal with this propagator we will take the following canonical transformations
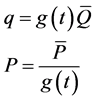 (9)
(9)
With the generating function 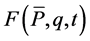
![]() (10)
(10)
Then (8) will be (see [22] )
![]() (11)
(11)
Since ![]() is an arbitrary function it will be chosen such that the second term in the Hamiltonian will be zero or
is an arbitrary function it will be chosen such that the second term in the Hamiltonian will be zero or
![]() (12)
(12)
In the exponent and by integrating the first term by part, then following by the integration over q we get the following condition
![]() (13)
(13)
which implies that ![]() should be a constant. Then the propagator Equation (11) will take the form
should be a constant. Then the propagator Equation (11) will take the form
![]() (14)
(14)
Using the formula
![]() (15)
(15)
one can finds that
![]() (16)
(16)
By inserting this into Equation (4) we will find the expression of the propagator related to Equation (1)
![]() (17)
(17)
which is the desired result
3. The Models
We would like to present a class of time dependent Harmonic oscillators with constant mass and varied frequencies, and we will follow the way that given above to find the exact propagator of the related system. Let us present the following Hamiltonian
![]() (18)
(18)
where ![]() is an arbitrary function, a and b are constants. The systems have been chosen such that function
is an arbitrary function, a and b are constants. The systems have been chosen such that function ![]() has a definite integration. To find the exact propagator related to this system we will chose the function
has a definite integration. To find the exact propagator related to this system we will chose the function ![]() Equation (3) to be
Equation (3) to be
![]() (19)
(19)
Then the propagator related to this system can has the following expression
![]() (20)
(20)
Then we will present the following canonical transformations
![]() (21)
(21)
where P and q are the new momentum and position. This will lead to a new expression of the propagator Equation (20)
![]() (22)
(22)
From here it is clear why the condition ![]() has been chosen to be a definite integration.
has been chosen to be a definite integration.
Examples
・ ![]()
The related function for this frequency is ![]()
・ ![]()
The related function for this frequency is ![]()
・ ![]()
The related function for this frequency is ![]()
・ ![]()
This frequency has a more generalized form than that given in [19] , where ![]() and the related function for this frequency is
and the related function for this frequency is![]() . This example
. This example ![]() does not have a definite integration for all values of r.
does not have a definite integration for all values of r.
where r, v and t0 are constants with t0 has the dimension of time.
4. Summery
The problem of the time dependent harmonic oscillator has been presented in this work. By using canonical transformations we could reach Equation (11) with the condition Equation (2), then using delta functional integration that gave us the condition Equation (13) of the momentum conservation, which can be generalized to be ![]() if the term
if the term ![]() exists in the Hamiltonian Equation (1), which represents the forced harmonic oscillator. In the last part some examples have been presented with their convenient transformations. The same problem with an inverse quadratic potential can be done by the same way given in this paper.
exists in the Hamiltonian Equation (1), which represents the forced harmonic oscillator. In the last part some examples have been presented with their convenient transformations. The same problem with an inverse quadratic potential can be done by the same way given in this paper.
Acknowledgements
We thank the Editor and the referee for their comments and support that is greatly appreciated.