Received 18 December 2015; accepted 23 February 2016; published 26 February 2016

1. Introduction: Student’s t Increments
The interest of this paper is independent Student’s t increments. These increments are independent draws from a Student’s t-distribution with support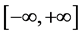 , a truncated Student’s t -distribution with support
, a truncated Student’s t -distribution with support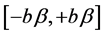 , or an effectively truncated Student’s t-distribution with support
, or an effectively truncated Student’s t-distribution with support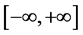 , but which has a multiplicative
, but which has a multiplicative 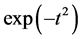 envelope which effectively truncates the distribution. Here
envelope which effectively truncates the distribution. Here 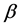 is the scale parameter for the Stu- dent’s t-distribution and
is the scale parameter for the Stu- dent’s t-distribution and 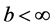 is a real constant.
is a real constant.
These independent Student’s t increments can be used to generate a random walk such as the Markov sequence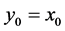 ,
, 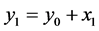 ,
, 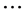 ,
, 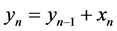 , where the
, where the 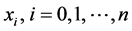 are independent draws from a Student’s t-distribution, a truncated Student’s t-distribution, or an effectively truncated Student’s t-distribution.
are independent draws from a Student’s t-distribution, a truncated Student’s t-distribution, or an effectively truncated Student’s t-distribution.
Attention will be restricted to Student’s t-distributions with location parameter (i.e., mean) , scale factor
, scale factor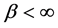 , and shape parameter
, and shape parameter![]() , which cover the Cauchy distribution, for which
, which cover the Cauchy distribution, for which![]() , to the Gaussian or normal distribution, for which
, to the Gaussian or normal distribution, for which![]() .
.
To distinguish between time t and and a realization of a random variable that is distributed as a Student’s t-distribution, a bold face t will be used with the name of the distribution and a regular face t will represent time. The symbols x and ![]() will represent random variables, and specific realizations of the random variables x and
will represent random variables, and specific realizations of the random variables x and ![]() will be represented as x and
will be represented as x and![]() . A stochastic process, which is a family of functions of time, is then
. A stochastic process, which is a family of functions of time, is then ![]() whereas
whereas ![]() is a random variable for
is a random variable for ![]() some constant and
some constant and ![]() is a number in that both t and the value of
is a number in that both t and the value of ![]() are specified.
are specified.
A Student’s t-distribution with location parameter![]() , shape parameter
, shape parameter![]() , and scale parameter
, and scale parameter![]() , is given by [1] - [3]
, is given by [1] - [3]
![]() (1)
(1)
with![]() .
. ![]() gives the probability that a random draw
gives the probability that a random draw ![]() from the Student’s t-dis- tribution lies in the interval
from the Student’s t-dis- tribution lies in the interval![]() .
.
A truncated Student’s t-distribution ![]() with location parameter
with location parameter![]() , shape parameter
, shape parameter![]() , and scale parameter
, and scale parameter![]() , is given by
, is given by
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
where the rectangle function ![]() if
if ![]() and
and ![]() for
for ![]() has been used to truncate the
has been used to truncate the
distribution and limit support to![]() .
.
A Student’s t-distribution is obtained from a mixture of a normal distribution with a standard deviation ![]() that is distributed as inverse chi with support
that is distributed as inverse chi with support ![]() [4] -[7] . Let
[4] -[7] . Let![]() , then a is distributed as chi,
, then a is distributed as chi, ![]() , and
, and
![]() (5)
(5)
Using chi as defined above and a normal distribution with zero mean and standard deviation of![]() , the mixing integral when evaluated from
, the mixing integral when evaluated from ![]() to
to ![]() yields a Student’s t-distribution
yields a Student’s t-distribution
![]() (6)
(6)
with a mean of zero, shape parameter![]() , and a scale parameter of
, and a scale parameter of![]() .
.
The probability that![]() ,
, ![]() , is needed to normalize properly a truncated chi distribution. A left-truncated chi distribution
, is needed to normalize properly a truncated chi distribution. A left-truncated chi distribution ![]() is zero for values
is zero for values![]() :
:
![]() (7)
(7)
An effectively truncated Student’s t-distribution ![]() is the pdf for a mixture of a left-truncated chi and normal distribution:
is the pdf for a mixture of a left-truncated chi and normal distribution:
![]() (8)
(8)
![]() is a Student’s t-distribution with shape parameter
is a Student’s t-distribution with shape parameter ![]() and scale parameter
and scale parameter![]() .
.
This paper is organized as follows. The development in time of the variance for the sum of independent draws from distributions is reviewed in Section 2. It is shown that truncation of a Student’s t-distribution keeps the moments finite and thus variances add, even if the distributions are not stable under convolution. Gaussian and Cauchy distributions are stable under self-convolution. A Gaussian convolved with a Gaussian yields a Gaussian. Student’s t-distributions other than ![]() and
and ![]() distributions are not stable under self-convolution. The tails of the self-convolution of Student’s t-distributions are “stable”; only the deep tails retain the characteristic
distributions are not stable under self-convolution. The tails of the self-convolution of Student’s t-distributions are “stable”; only the deep tails retain the characteristic ![]() power-law dependence of the original t-distribution [6] [8] [9] . However, the fact that the moments are finite and variances add under convolution allows the time development of the variance to be determined. Examples of smoothing of the characteristic function owing to truncation are given and examples of the mo- ments of distributions are given.
power-law dependence of the original t-distribution [6] [8] [9] . However, the fact that the moments are finite and variances add under convolution allows the time development of the variance to be determined. Examples of smoothing of the characteristic function owing to truncation are given and examples of the mo- ments of distributions are given.
The continuity of sample paths is discussed in Section 3. It is shown that truncated and effectively truncated Student’s t-distributions have continuous sample paths. It is also shown that sample paths created by Student’s t-distributions with ![]() have continuous sample paths. Random walks are shown for independent increments drawn from a uniform distribution, from a normal distribution, and from
have continuous sample paths. Random walks are shown for independent increments drawn from a uniform distribution, from a normal distribution, and from ![]() and
and ![]() Student’s t-distri- butions. The samples paths for the different distributions were all simulated from the same sequence of pseudo random numbers. This enables observation of the effects of different shape parameters and truncations on the random walks.
Student’s t-distri- butions. The samples paths for the different distributions were all simulated from the same sequence of pseudo random numbers. This enables observation of the effects of different shape parameters and truncations on the random walks.
Section 4 is a conclusion.
2. Variances Add under Convolution
Let g and h be zero mean probability density functions (pdf’s) with variances ![]() and
and![]() , and let
, and let ![]() be the convolution of g and h:
be the convolution of g and h:
![]() (9)
(9)
![]() is also a zero mean pdf and hence the variance of
is also a zero mean pdf and hence the variance of ![]() is
is
![]() (10)
(10)
where ![]() is the
is the ![]() Fourier transform of
Fourier transform of![]() . From the convolution theorem,
. From the convolution theorem, ![]() , and
, and
![]() (11)
(11)
since g and h are zero-mean pdf’s:![]() ,
, ![]() , and
, and
![]() ,
,![]() . Thus
. Thus
![]() (12)
(12)
and variances add under convolution. The argument holds even if the means for g and h are non-zero. The argument also holds for distributions that are stable or are not-stable under convolution, or for combinations of distributions that might not retain shape under the action of convolution.
The Fourier transforms![]() , and
, and ![]() will exist for pdf’s that are continuous or have finite dis- continuities [10] p. 9. The derivatives of the transforms might not exist at some values of s owing to higher- order discontinuities, but truncation of the pdf will smooth the transform and remove the discontinuities. For
will exist for pdf’s that are continuous or have finite dis- continuities [10] p. 9. The derivatives of the transforms might not exist at some values of s owing to higher- order discontinuities, but truncation of the pdf will smooth the transform and remove the discontinuities. For
example, consider![]() . This distribution in the x domain is a Cauchy
. This distribution in the x domain is a Cauchy
distribution. The derivatives in the transform domain do not exist at![]() . However, provided that
. However, provided that![]() , derivatives at
, derivatives at ![]() exist for the convolution
exist for the convolution
![]() (13)
(13)
which is the Fourier transform of the truncated distribution,
![]() (14)
(14)
where ![]() if
if ![]() and
and ![]() for
for![]() .
.
The convolution of Equation (13) does not appear to have an analytic expression except at![]() .
.
An expression for the convolution, Equation (13), can be written for ![]() as
as
![]() (15)
(15)
from which the derivatives at ![]() can, with some effort, be calculated. For
can, with some effort, be calculated. For![]() ,
, ![]() and
and
![]() (16)
(16)
![]() (17)
(17)
The smoothing power of the convolution of Equation (13) can be observed if the sinc function is replaced by a unit area rectangle function with a similar width as the main lobe of the sinc function. Using this approximation for the sinc function, the convolution of Equation (13) becomes
![]() (18)
(18)
![]() (19)
(19)
and can be evaluated to give
![]() (20)
(20)
which is, for![]() , a continuous function of s and for which derivatives exist at
, a continuous function of s and for which derivatives exist at![]() . This stands in stark contrast to the Fourier transform for the not-truncated function (i.e., for
. This stands in stark contrast to the Fourier transform for the not-truncated function (i.e., for![]() ), which is
), which is ![]() .
.
Figure 1 shows the effect of convolution on the Fourier transform of a Cauchy distribution. The Cauchy dis- tribution was truncated as indicated in Equation (14) with T = 100. The scale parameter of the Cauchy distri- bution of Equation (14) is![]() . The truncation thus removes values that have magnitudes greater than
. The truncation thus removes values that have magnitudes greater than ![]() times the scale factor. The probability of an observation with magnitude >50 is 0.002, i.e.,
times the scale factor. The probability of an observation with magnitude >50 is 0.002, i.e., ![]() , for the distribution of Equation (14). For a normally distributed random variable with mean
, for the distribution of Equation (14). For a normally distributed random variable with mean ![]() and standard deviation
and standard deviation![]() ,
,![]() .
.
Figure 2 shows similar quantities as Figure 1 but with![]() . The probability of an observation with magnitude >5000 is
. The probability of an observation with magnitude >5000 is ![]() for the Cauchy distribution of Equation (14). In a “normal” world,
for the Cauchy distribution of Equation (14). In a “normal” world, ![]() . Truncation smooths the characteristic function and keeps moments finite.
. Truncation smooths the characteristic function and keeps moments finite.
The variance ![]() of an n-fold convolution,
of an n-fold convolution, ![]() , is
, is![]() . If
. If![]() , then the variance for the n-fold self-convolution is
, then the variance for the n-fold self-convolution is![]() . The pdf for the sum of n-independent draws from the same parent distribution that is characterized by a pdf f with variance
. The pdf for the sum of n-independent draws from the same parent distribution that is characterized by a pdf f with variance ![]() is the n-fold self-convolution of the parent pdf f and the variance of the sum of the n-independent draws is
is the n-fold self-convolution of the parent pdf f and the variance of the sum of the n-independent draws is![]() . For a process that is the summation of samples that are periodically drawn from a parent population, the variance of the process would be proportional to time.
. For a process that is the summation of samples that are periodically drawn from a parent population, the variance of the process would be proportional to time.
Following Papoulis [11] p. 292, consider a homogenous and stationary Markov sequence [11] p. 530![]() ,
, ![]() ,
, ![]() ,
, ![]() , where the
, where the![]() , are independent Student’s t increments, i.e., the
, are independent Student’s t increments, i.e., the ![]() are independent draws from a Student’s t-distribution. The sequence is homogeneous since the pdf’s for each
are independent draws from a Student’s t-distribution. The sequence is homogeneous since the pdf’s for each ![]() are independent of n. The sequence is stationary since it is homogeneous and all
are independent of n. The sequence is stationary since it is homogeneous and all ![]() have the
have the
same pdf. Let ![]() be the time between increments. The total time t taken to acquire the sequence
be the time between increments. The total time t taken to acquire the sequence ![]() is
is![]() . The mean of
. The mean of ![]() is zero and the variance of
is zero and the variance of![]() ,
, ![]() , is
, is
![]() (21)
(21)
where ![]() is the variance of any of the Student’s t increments
is the variance of any of the Student’s t increments![]() . Allow
. Allow![]() , which requires
, which requires![]() . The variance will remain finite and non-zero only if
. The variance will remain finite and non-zero only if ![]() as
as![]() , where
, where ![]() is a constant. Thus
is a constant. Thus ![]() varies linearly with sampling period
varies linearly with sampling period ![]() and the variance of the sequence
and the variance of the sequence ![]() varies linearly with time t.
varies linearly with time t.
The linear dependence on time of the variance of the Markov sequence ![]() arises not because of Gaussian properties, but because of the assumed independence of samples. The variance of a summation of independent samples is the sum of the variance of each sample, and thus the variance will increase linearly with the number of samples. If the samples are obtained by periodic sampling, then the variance will increase linearly with time.
arises not because of Gaussian properties, but because of the assumed independence of samples. The variance of a summation of independent samples is the sum of the variance of each sample, and thus the variance will increase linearly with the number of samples. If the samples are obtained by periodic sampling, then the variance will increase linearly with time.
Papoulis [11] p. 292 writes that the limit as![]() , which requires
, which requires![]() , results in a Wiener-Lévy process, which is a stochastic process that is continuous for almost all outcomes. Papoulis then shows
, results in a Wiener-Lévy process, which is a stochastic process that is continuous for almost all outcomes. Papoulis then shows ![]() is a normally distributed random variable. Papoulis assumed n samples were drawn from a binomial distribution
is a normally distributed random variable. Papoulis assumed n samples were drawn from a binomial distribution
with ![]() and appealed to the DeMoivre-Laplace theorem to obtain a normal distribution in the limit that
and appealed to the DeMoivre-Laplace theorem to obtain a normal distribution in the limit that
![]() [11] , p. 66.
[11] , p. 66.
Not all functions tend to a normal pdf under repeated convolution [10] , p. 186. A Cauchy distribution is probably the most noted distribution that does not follow the central limit theorem. Not all Student’s t-distri- butions tend to a normal distribution. According to Bracewell [10] , p. 190, only functions with finite area, finite mean, and finite second moments will tend to normal distributions under repeated convolution. For convolution of non-identical functions, Lyapunov’s condition on the ratio of absolute moments to power of the variance must be satisfied.
The dependence on time of the variance for the Markov sequence ![]() can be obtained in a slightly different manner than the approach of Papoulis [11] and in a manner that does not specify the underlying pdf’s. Following Shreve [12] , p. 98, the expectation of the quadratic variation can be calculated
can be obtained in a slightly different manner than the approach of Papoulis [11] and in a manner that does not specify the underlying pdf’s. Following Shreve [12] , p. 98, the expectation of the quadratic variation can be calculated
![]() (22)
(22)
and the mean-square limit of the variance of the quadratic variation can be used to show convergence.
The variance of Q is![]() . The fourth central moment,
. The fourth central moment,
![]() , is proportional to the variance squared for a Student’s t-distribution (see below) and there-
, is proportional to the variance squared for a Student’s t-distribution (see below) and there-
fore ![]() is a constant. The variance of Q is then
is a constant. The variance of Q is then![]() , which tends to zero linearly with
, which tends to zero linearly with ![]() as
as![]() . Thus in a mean-square sense, the expectation of the quadratic variation is
. Thus in a mean-square sense, the expectation of the quadratic variation is![]() , i.e.,
, i.e.,![]() . The variance of the stochastic process increases linearly with time t. For Gaussian increments,
. The variance of the stochastic process increases linearly with time t. For Gaussian increments,![]() . For Student’s t increments,
. For Student’s t increments, ![]() is a simple function of the shape parameter
is a simple function of the shape parameter![]() , the scale parameter
, the scale parameter![]() , and the degree and form of truncation of the underlying pdf.
, and the degree and form of truncation of the underlying pdf.
As the moments and continuity of a stochastic process are of interest, these topics are covered in the following sections. In the following, it is assumed on the strength of the arguments in this section and owing to the assumption of independent increments, that the scale factor ![]() varies as
varies as![]() . The scale factor for a normal distribution is
. The scale factor for a normal distribution is![]() , the standard deviation. For Brownian motion,
, the standard deviation. For Brownian motion, ![]() is a normally distributed random variable and
is a normally distributed random variable and![]() . For Brownian motion the increments are independent, Gaussian random variables.
. For Brownian motion the increments are independent, Gaussian random variables.
2.1. Moments for Student’s t-Distributions With Support ![]()
The ![]() central moment for a Student’s t-distribution with support
central moment for a Student’s t-distribution with support ![]() is given by
is given by
![]() (23)
(23)
Closed form expressions for the second, fourth, and sixth central moment are given, along with the values of ![]() for which the expressions are valid.
for which the expressions are valid.
The second central moment![]() , which is the variance
, which is the variance![]() , is proportional to
, is proportional to ![]() and is valid for
and is valid for![]() :
:
![]() (24)
(24)
The fourth central moment ![]() is proportional to
is proportional to ![]() and is valid for
and is valid for![]() :
:
![]() (25)
(25)
The sixth central moment ![]() is proportional to
is proportional to ![]() and is valid for
and is valid for![]() :
:
![]() (26)
(26)
Not all central moments exist when the region of support for the t-distribution is![]() .
.
2.2. Moments for Truncated Student’s t-Distributions With Support ![]()
Truncation of Student’s t-distributions keeps the moments finite and defined [6] [7] . As an example, consider a Student’s t-distribution with one degree of freedom, ![]() , (i.e., a Cauchy or Lorentzian distribution) with support
, (i.e., a Cauchy or Lorentzian distribution) with support ![]() where
where ![]() is a scale parameter and b is a number. Provided that
is a scale parameter and b is a number. Provided that![]() , central moments for the truncated Cauchy (and for all other truncated Student’s t-distributions with
, central moments for the truncated Cauchy (and for all other truncated Student’s t-distributions with![]() ) exist.
) exist.
The integrals that define the truncated central moment for the ![]() Student’s t-distribution are
Student’s t-distribution are
![]() (27)
(27)
![]() (28)
(28)
Closed form expressions for the central moments for a truncated ![]() distribution are given. As might be expected,
distribution are given. As might be expected, ![]() with
with ![]() is proportional to
is proportional to ![]() with a constant of proportionality that is a function of b and n.
with a constant of proportionality that is a function of b and n.
For truncated ![]() Student’s t-distributions, the second central moment
Student’s t-distributions, the second central moment ![]() is
is
![]() (29)
(29)
the fourth central moment ![]() is
is
![]() (30)
(30)
and the sixth central moment ![]() is
is
![]() (31)
(31)
All of these moments are defined with the single restriction that ![]() (i.e., that the
(i.e., that the ![]() distribution is truncated). Since the tails of distributions for
distribution is truncated). Since the tails of distributions for ![]() decrease more rapidly than for a
decrease more rapidly than for a ![]() distribution, the central moments can be evaluated for all truncated Student’s t-distributions with
distribution, the central moments can be evaluated for all truncated Student’s t-distributions with![]() . In this sense, the Cauchy distribution is a worst case.
. In this sense, the Cauchy distribution is a worst case.
3. Continuous Sample Paths
For a Markov process, the sample paths are continuous functions of t, if for any![]() ,
,
![]() (32)
(32)
uniformly in![]() , and
, and ![]() [13] , p. 46.
[13] , p. 46. ![]() is the pdf for the process and t is time.
is the pdf for the process and t is time.
The condition for continuous sample paths, Equation (32), can be written in different forms. For independent, zero mean (![]() ), symmetric pdf’s
), symmetric pdf’s
![]() (33)
(33)
or equivalently, since ![]() for
for![]() ,
,
![]() (34)
(34)
Both forms will be used.
A stochastic process that is created as the sums of independent draws from a normal distribution (i.e., Gaussian increments) with variance ![]() and mean z has continuous sample paths. For simplicity in no- tation, assume that
and mean z has continuous sample paths. For simplicity in no- tation, assume that![]() . For this process with pdf given by
. For this process with pdf given by
![]() (35)
(35)
the limit
![]() (36)
(36)
![]() (37)
(37)
![]() (38)
(38)
equals zero and the sample paths are continuous.
An expansion of Equation (38) about ![]() shows that the dominant term goes as
shows that the dominant term goes as![]() :
:
![]() (39)
(39)
and thus the limiting value as ![]() is zero.
is zero.
For samples paths that are created as the sums of independent draws from a Student’s t-distribution with ![]() (i.e.,
(i.e., ![]() Student’s t increments), which is a Cauchy distribution, the pdf
Student’s t increments), which is a Cauchy distribution, the pdf
![]() (40)
(40)
does not have continuous sample paths. The limit
![]() (41)
(41)
![]() (42)
(42)
does not equal zero. An expansion of ![]() about
about ![]()
![]() (43)
(43)
shows that the dominant term is ![]() and thus the limit is infinity as
and thus the limit is infinity as![]() .
.
Sample paths for both normal distributions and ![]() Student’s t-distributions (Cauchy) have
Student’s t-distributions (Cauchy) have
![]() (44)
(44)
as required for consistency [13] , p. 47.
For a process with ![]() Student’s t-distribution increments, the sample paths are continuous if the limit
Student’s t-distribution increments, the sample paths are continuous if the limit
![]() (45)
(45)
![]() (46)
(46)
![]() (47)
(47)
is zero. Since the limit is not zero, a process with ![]() Student’s t-distribution increments does not have con- tinuous paths.
Student’s t-distribution increments does not have con- tinuous paths.
For a process with ![]() Student’s t-distribution increments, the sample paths are continuous if the limit
Student’s t-distribution increments, the sample paths are continuous if the limit
![]() (48)
(48)
![]() (49)
(49)
![]() (50)
(50)
is zero.
An expansion about ![]() shows that the dominant term for the condition for continuous sample paths for a
shows that the dominant term for the condition for continuous sample paths for a ![]() Student’s t-distribution, Equation (50), is
Student’s t-distribution, Equation (50), is ![]() as
as![]() :
:
![]() (51)
(51)
Processes with Student’s t-distributions increments with ![]() have continuous paths since the limit as
have continuous paths since the limit as![]() . However, the fourth moments for Student’s t-distributions with
. However, the fourth moments for Student’s t-distributions with ![]() do not exist. Thus it would not be possible to use the mean-square variance of the quadratic variation to prove convergence of the ex- pecation of the quadratic variation
do not exist. Thus it would not be possible to use the mean-square variance of the quadratic variation to prove convergence of the ex- pecation of the quadratic variation ![]() to
to![]() . See Equation (22) and associated discussion. The moments exist for truncated and effectively truncated Student’s t-distributions.1
. See Equation (22) and associated discussion. The moments exist for truncated and effectively truncated Student’s t-distributions.1
3.1. Sample Paths: Truncated Cauchy
Consider a truncated Cauchy with support![]() , or
, or ![]() with
with![]() .
.
The variance for a truncated Cauchy with support ![]() is given by Equation (29) since the mean is zero and truncation keeps the integral finite. The truncation need not be severe to obtain useful results; the variance diverges linearly with b.
is given by Equation (29) since the mean is zero and truncation keeps the integral finite. The truncation need not be severe to obtain useful results; the variance diverges linearly with b.
The condition for continuity is that the limit
![]() (52)
(52)
![]() (53)
(53)
equals zero for any![]() . The rectangle function,
. The rectangle function, ![]() if
if ![]() and
and ![]() otherwise, has been used to truncate the distribution.
otherwise, has been used to truncate the distribution.
If![]() , then the limit is zero and a process with truncated Cauchy increments should have a continuous path. However, it is not clear that the limit is zero for any
, then the limit is zero and a process with truncated Cauchy increments should have a continuous path. However, it is not clear that the limit is zero for any![]() . The limit is zero when all the area of the pdf is enclosed by
. The limit is zero when all the area of the pdf is enclosed by ![]() for any
for any![]() . In fact, the limit is zero only for
. In fact, the limit is zero only for ![]() equal to “infinity”, since the maximum value (i.e., “infinity”) allowed is
equal to “infinity”, since the maximum value (i.e., “infinity”) allowed is![]() . Support for the truncated Cauchy distribution was taken as
. Support for the truncated Cauchy distribution was taken as ![]() . The support was chosen to scale with the scale factor of the distribution so that the distri- bution was truncated to include the same fraction of the area of the not-truncated distribution, regardless of the choice of the scale factor
. The support was chosen to scale with the scale factor of the distribution so that the distri- bution was truncated to include the same fraction of the area of the not-truncated distribution, regardless of the choice of the scale factor![]() . That is, the truncation was chosen such that the value of
. That is, the truncation was chosen such that the value of![]() , which is defined by Equation (28), is independent of the scale factor.
, which is defined by Equation (28), is independent of the scale factor.
3.2. Sample Paths: Effectively Truncated n = 1 Distribution
The pdf for a mixture of a left-truncated chi distribution for![]() ,
, ![]() ,
, ![]() , and a normal distribution is [6] , [7]
, and a normal distribution is [6] , [7]
![]() (54)
(54)
The tails of the pdf decrease as ![]() for non-zero q, where
for non-zero q, where ![]() is the maximum value of
is the maximum value of ![]() that is included in the mixing integral.
that is included in the mixing integral.
The condition for continuous sample paths for ![]() can be written in several equivalent forms:
can be written in several equivalent forms:
![]() (55)
(55)
which, owing to symmetry in![]() , is equivalent to
, is equivalent to
![]() (56)
(56)
The equation can be written as
![]() (57)
(57)
Consider the inequality
![]() (58)
(58)
An analytic expression for the integral of the upper bound of the inequality can be found. The dominant term in a series expansion for
![]() (59)
(59)
about ![]() with
with![]() , where
, where ![]() is a positive number, is
is a positive number, is
![]() (60)
(60)
and the limit
![]() (61)
(61)
for![]() . The scaling
. The scaling ![]() ensures that the truncation scales appropriately with S and thus keeps constant the area in the tails of the pdf that has been truncated.
ensures that the truncation scales appropriately with S and thus keeps constant the area in the tails of the pdf that has been truncated.
Since probability is![]() , i.e.,
, i.e., ![]() , and the limit as
, and the limit as ![]() of the integral of the upper bound times S is zero, then
of the integral of the upper bound times S is zero, then
![]() (62)
(62)
and the sample paths for stochastic processes that are created by summing independent draws from effectively truncated ![]() Student’s t-distributions (i.e., effectively truncated Cauchy distributions) are continuous. The same reasoning can be applied to all effectively truncated Student’s t-distributions with
Student’s t-distributions (i.e., effectively truncated Cauchy distributions) are continuous. The same reasoning can be applied to all effectively truncated Student’s t-distributions with ![]() and thus all stochastic processes created by summing independent draws from effectively truncated Student’s t-distributions have continuous sample paths.
and thus all stochastic processes created by summing independent draws from effectively truncated Student’s t-distributions have continuous sample paths.
Figure 3 is composed of random walks wherein the increments for the walks were obtained from a uniform distribution, a normal distribution, and ![]() distributions. All walks were manufactured from the same se- quence of 2048 draws from a uniform distribution. This allows comparison of the walks and demonstrates the moderating influence of truncation and effective truncation on the walks. The parameter b was arbitrarily chosen to equal 50 and q = 0.025 was chosen to match approximately quadratic variation for the walks for the truncated and effectively truncated
distributions. All walks were manufactured from the same se- quence of 2048 draws from a uniform distribution. This allows comparison of the walks and demonstrates the moderating influence of truncation and effective truncation on the walks. The parameter b was arbitrarily chosen to equal 50 and q = 0.025 was chosen to match approximately quadratic variation for the walks for the truncated and effectively truncated ![]() distributions. The walks with truncated and effectively truncated
distributions. The walks with truncated and effectively truncated ![]() increments are more angular than the walk with normal increments. The
increments are more angular than the walk with normal increments. The ![]() walk shows the occasional large jump. The magnitudes of the jumps are significantly smaller in the truncated and effectively truncated
walk shows the occasional large jump. The magnitudes of the jumps are significantly smaller in the truncated and effectively truncated ![]() walks. Note that the
walks. Note that the ![]() increments were scaled for presentation of the walks in the figure. See Table 1 and
increments were scaled for presentation of the walks in the figure. See Table 1 and
![]()
Table 1. Descriptive statistics for 2048 draws from distributions with ![]() and
and![]() .
.
Table 2 for sample and parent statistics of the distributions used to generate the figures. For a Cauchy distri- bution with![]() ,
,![]() . For a normal distribution,
. For a normal distribution,![]() .
.
Figure 4 displays the pdf’s on a ![]() plot. This figure clearly shows that there is little difference be- tween the truncated and effectively truncated
plot. This figure clearly shows that there is little difference be- tween the truncated and effectively truncated ![]() pdf for
pdf for ![]() where b is the point of truncation. The tail of the truncated distribution falls off infinitely fast whereas the tails of the effectively truncated distribution fall off at the same rate as a Gaussian pdf. Since the random walk with Gaussian increments has continuous sample paths, one would expect an effectively truncated
where b is the point of truncation. The tail of the truncated distribution falls off infinitely fast whereas the tails of the effectively truncated distribution fall off at the same rate as a Gaussian pdf. Since the random walk with Gaussian increments has continuous sample paths, one would expect an effectively truncated ![]() distribution to have continuous sample paths as the roll- off of the tails is similar. And since the tails of the truncated
distribution to have continuous sample paths as the roll- off of the tails is similar. And since the tails of the truncated ![]() distribution roll-off faster than a Gaussian, one would expect a truncated
distribution roll-off faster than a Gaussian, one would expect a truncated ![]() walk to have continuous sample paths. The tails of the Cauchy distribution (i.e., a not truncated
walk to have continuous sample paths. The tails of the Cauchy distribution (i.e., a not truncated ![]() Student’s t-distribution) do not roll off as fast as a Gaussian. A Cauchy random walk does not have continuous samples paths. Large steps in the Cauchy random walk are obvious in Figure 3.
Student’s t-distribution) do not roll off as fast as a Gaussian. A Cauchy random walk does not have continuous samples paths. Large steps in the Cauchy random walk are obvious in Figure 3.
There is little difference in shape between a truncated Student’s t-distribution and an effectively truncated Student’s t-distribution. From taking limits of the pdf, continuous sample paths were found for the effectively truncated ![]() distribution, yet a truncated
distribution, yet a truncated ![]() distribution did not appear to have continuous sample paths (c.f. Equation (53) and related discussion). This discrepancy would seem to point to a problem with the con- dition for continuous sample paths or the interpretation of the condition for continuous sample paths.
distribution did not appear to have continuous sample paths (c.f. Equation (53) and related discussion). This discrepancy would seem to point to a problem with the con- dition for continuous sample paths or the interpretation of the condition for continuous sample paths.
![]()
Table 2. Parent statistics for distributions with![]() , and
, and![]() .
.
3.3. Sample Paths: Effectively Truncated n = 3 Student’s t-Distribution
The pdf for a mixture of a left-truncated chi distribution for![]() ,
, ![]() ,
, ![]() , and a normal distribution is [6] [7]
, and a normal distribution is [6] [7]
![]() (63)
(63)
The left truncation of the chi distribution imparts a multiplicative Gaussian envelope that effectively truncates the underlying t distribution.
Figure 5 displays a normal pdf and ![]() pdfs on a
pdfs on a ![]() plot. Note the similarity between the
plot. Note the similarity between the ![]() distribution, the truncated
distribution, the truncated ![]() distribution, and the effectively truncated
distribution, and the effectively truncated ![]() distribution for
distribution for ![]() where
where ![]() is the point of truncation. The value of
is the point of truncation. The value of ![]() was chosen to yield approximately the same standard deviation for the effectively truncated distribution as was obtained with the truncated distri- bution. See Table 1 and Table 2 for sample and parent statistics of the distributions. The effectively truncated distribution is just starting to show the same slope in the tail as the normal distribution. This owes to the
was chosen to yield approximately the same standard deviation for the effectively truncated distribution as was obtained with the truncated distri- bution. See Table 1 and Table 2 for sample and parent statistics of the distributions. The effectively truncated distribution is just starting to show the same slope in the tail as the normal distribution. This owes to the ![]() characteristic from truncation of the underlying
characteristic from truncation of the underlying ![]() distribution in the
distribution in the ![]() -normal mixture that creates the Student’s distribution. For a
-normal mixture that creates the Student’s distribution. For a ![]() t-distribution with
t-distribution with![]() . For a normal dis- tribution,
. For a normal dis- tribution,![]() .
.
Figure 6 is similar to Figure 3 except increments were drawn from ![]() Student’s t-distributions and the walks were not scaled. There are five random walks displayed in Figure 6: a walk with uniform increments (red), a walk with normal increments (black), and walks with
Student’s t-distributions and the walks were not scaled. There are five random walks displayed in Figure 6: a walk with uniform increments (red), a walk with normal increments (black), and walks with ![]() increments (not-truncated, truncated, and effectively truncated). The three
increments (not-truncated, truncated, and effectively truncated). The three ![]() walks almost perfectly overlap, showing that the walks are almost iden- tical, as one might surmise from Figure 5. The normal walk and the
walks almost perfectly overlap, showing that the walks are almost iden- tical, as one might surmise from Figure 5. The normal walk and the ![]() sample paths appear to have similar features. Figure 7 displays random walks with uniform increments, with Gaussian increments, and with
sample paths appear to have similar features. Figure 7 displays random walks with uniform increments, with Gaussian increments, and with ![]() truncated increments. All walks were created from the same 2048 random draws from a uniform distribution. The sample paths for the Gaussian increments are displayed twice; once with a scale factor of 1 and once with a scale factor of 1.693. The multiplicative scale factor of 1.693 is the ratio of standard deviations of the increments for the parent distributions of the normal and truncated
truncated increments. All walks were created from the same 2048 random draws from a uniform distribution. The sample paths for the Gaussian increments are displayed twice; once with a scale factor of 1 and once with a scale factor of 1.693. The multiplicative scale factor of 1.693 is the ratio of standard deviations of the increments for the parent distributions of the normal and truncated ![]() distributions. The scaled plot is presented to facilitate comparison of the truncated
distributions. The scaled plot is presented to facilitate comparison of the truncated ![]() and normal sample paths. It is clear that the
and normal sample paths. It is clear that the ![]() and normal sample paths (for the 2048 time steps displayed) are similar.
and normal sample paths (for the 2048 time steps displayed) are similar.
All walks shown in Figure 3, Figure 6, and Figure 7 were manufactured from the same sequence of variates drawn from a uniform distribution. This allows comparison of the effect of different distributions (uniform,
Gaussian, Cauchy, ![]() and
and ![]() distributions) and truncation (both truncation by a rectangle function and effective truncation) on the sample paths.
distributions) and truncation (both truncation by a rectangle function and effective truncation) on the sample paths.
Table 1 lists descriptive statistics for the draws that were used to create the sample paths shown in Figure 3, Figure 6, and Figure 7. Table 2 lists the values found in Table 1, but calculated for the parent distributions. In Table 1 and Table 2, Q is the quadratic variation and ![]() is the average quadratic variation per step. There is good correspondence between the values obtained for the sample parameters and the parent parameters. In Table 2, the
is the average quadratic variation per step. There is good correspondence between the values obtained for the sample parameters and the parent parameters. In Table 2, the ![]() symbol indicates a value that was obtained by a symmetry argument.
symbol indicates a value that was obtained by a symmetry argument.
The data in Table 1 and Table 2, and in Figures 3-6, clearly show the effectiveness of truncation and effec- tive truncation.
4. Conclusions
Independent Student’s t increments, from which stochastic processes such as random walks are created, are investigated. Attention is restricted to increments from not-truncated, truncated, and effectively truncated Student’s t-distributions with shape parameters![]() , which covers a broad range of distributions: from Cauchy distributions, for which
, which covers a broad range of distributions: from Cauchy distributions, for which![]() , to normal or Gaussian distributions, for which
, to normal or Gaussian distributions, for which![]() . A Student’s t-distribution can be obtained as a mixture of a chi distribution of the reciprocal of
. A Student’s t-distribution can be obtained as a mixture of a chi distribution of the reciprocal of ![]() and a normal distribution with standard deviation of
and a normal distribution with standard deviation of![]() . Effectively truncated t-distributions arise from left-truncation of the chi distri- butions in the mixing integrals. An effectively truncated Student’s t-distribution has a Gaussian envelope that imparts interesting properties to the effectively truncated Student’s t-distribution.
. Effectively truncated t-distributions arise from left-truncation of the chi distri- butions in the mixing integrals. An effectively truncated Student’s t-distribution has a Gaussian envelope that imparts interesting properties to the effectively truncated Student’s t-distribution.
Random walks, specifically Markov sequences![]() ,
, ![]() ,
, ![]() ,
, ![]() , where the
, where the ![]() are independent Student’s t increments, are considered. The development in time of the scale parameter
are independent Student’s t increments, are considered. The development in time of the scale parameter ![]() of the Student’s t-distributions (not-truncated, truncated, and effectively truncated t-distributions) is investigated. It is found for distributions for which the variance exists that
of the Student’s t-distributions (not-truncated, truncated, and effectively truncated t-distributions) is investigated. It is found for distributions for which the variance exists that ![]() where
where ![]() is a constant and t is time. The variance exists for truncated and effectively truncated Student’s t-distributions, and for Student’s t-distributions with shape parameter
is a constant and t is time. The variance exists for truncated and effectively truncated Student’s t-distributions, and for Student’s t-distributions with shape parameter![]() . The development in time of the scale parameter for Student’s t-distributions is consistent with a normal distribution, for which the variance, which equals
. The development in time of the scale parameter for Student’s t-distributions is consistent with a normal distribution, for which the variance, which equals![]() , in- creases linearly with time. A Gaussian (or normal) distribution is stable under convolution; in general, a Student’s t-distribution is not stable under convolution.
, in- creases linearly with time. A Gaussian (or normal) distribution is stable under convolution; in general, a Student’s t-distribution is not stable under convolution.
The continuity of the sample paths is investigated and it is found that truncated and effectively truncated Student’s t-distributions, and that Student’s t-distributions with![]() , have continuous sample paths. This opens the possibility for modelling with a greater number of distributions.
, have continuous sample paths. This opens the possibility for modelling with a greater number of distributions.
Gardiner [13] , p. 79 defines a Wiener process ![]() as
as
![]() (64)
(64)
with the constraints that![]() , that
, that ![]() is a continuous function of time t, and that
is a continuous function of time t, and that ![]() is a Markov process. The requirement
is a Markov process. The requirement ![]() is not restrictive as any non-zero mean value of
is not restrictive as any non-zero mean value of ![]() can be considered to be signal. Gardner explains that one normally assumes that
can be considered to be signal. Gardner explains that one normally assumes that ![]() is Gaussian and that
is Gaussian and that![]() . The assumption of Gaussian statistics follows from a desire to have continuous paths for
. The assumption of Gaussian statistics follows from a desire to have continuous paths for![]() . The white noise property of the Wiener process, i.e.,
. The white noise property of the Wiener process, i.e., ![]() , follows not from the assumption of Gaussian statistics for
, follows not from the assumption of Gaussian statistics for ![]() but from the assumption that
but from the assumption that ![]() is a Markov process. For a Markov process,
is a Markov process. For a Markov process, ![]() is not determined probabilistically by any past values [13] , p. 78 and thus
is not determined probabilistically by any past values [13] , p. 78 and thus ![]() and
and ![]() are independent for all
are independent for all ![]() and
and![]() .
.
A random walk process that is constructed from truncated or effectively truncated Student’s t increments ![]() with
with ![]() is continuous. This process can also be constructed under the Markov assumption that
is continuous. This process can also be constructed under the Markov assumption that![]() , where for simplicity increments are assumed to be draws from zero mean dis- tributions such that
, where for simplicity increments are assumed to be draws from zero mean dis- tributions such that![]() . Student’s t-distributions with
. Student’s t-distributions with ![]() appear also to be continuous, without the need for truncation. Thus it appears that there exists more than independent Gaussian increments for construction of random walks with continuous sample paths. Given continuous sample paths and second mo- ments that depend linearly on time for random walks with independent, not-truncated, truncated, and effectively truncated Student’s t-increments, it seems reasonable to speculate that the diffusion coefficients [13] [14] , p. 79, p. 133
appear also to be continuous, without the need for truncation. Thus it appears that there exists more than independent Gaussian increments for construction of random walks with continuous sample paths. Given continuous sample paths and second mo- ments that depend linearly on time for random walks with independent, not-truncated, truncated, and effectively truncated Student’s t-increments, it seems reasonable to speculate that the diffusion coefficients [13] [14] , p. 79, p. 133
![]() (65)
(65)
exist and thus it should be possible to model noise in Langevin equations with appropriate t-distributions.
Acknowledgements
This work was funded by the Natural Science and Engineering Research Council (NSERC) Canada.