An Alternative Approach to AIC and Mallow’s Cp Statistic-Based Relative Influence Measures (RIMS) in Regression Variable Selection ()
Received 2 January 2016; accepted 20 February 2016; published 23 February 2016

1. Introduction
Model selection (variable selection) in regression has received great attention in literature in the recent times. A large number of predictors usually are introduced at the initial stage of modeling to attenuate possible modeling biases [1] . As noted by [2] , inference under models with too few parameters (variables) can be biased while with models having too many parameters (variables), there may be poor precision or identification of effects. Hence, the need for a balance between under- and over-fitted models is known as variable selection.
Influential observation is a special case of outliers. In the simplest sense, outlying or extreme values are observations which are well separated from the remainder of the data. Outliers result from either (1) the errors of measurement or (2) intrinsic variability (mean shift-inflation of variances or others) and appear either in the form of (i) change in the direction of response (Y) variable, (ii) deviation in the space of explanatory variables, deviated points in X-direction called leverage points or (iii) change in both the directions (direction of the explanatory variable(s) and the response variable). These outlying observations may involve large residuals and often have dramatic effects on the fitted least squares regression function. The influence of an individual case (data point) in a regression model can be adverse causing a significant shift (upward or downward) in the value of the parameters of a model in turn reducing the predictive power of the model. Only few papers dealing with the influence of individual data cases in regression explicitly take an initial variable selection step into account. This problem is handled by [3] -[6] .
One objective of regression variable selection is to reduce the predictors to some optimal subset of the available regressors [3] . In literature, several approaches of variable selection exist, which include the stepwise deletion and subset selection. Stepwise deletion includes regression models in which the choice of predictive variables is carried out by an automatic procedure. Usually, this takes the form of a sequence of F-tests or t-tests, but other techniques are possible, such as adjusted R-square, AIC, BIC, Mallow’s statistic, PRESS or false discovery rate [7] .
[8] proposed the coefficient of determination ratio (CDR) which was based on the value coefficient of determination (R2) of the linear regression model. [9] developed an outlier detection and robust selection method that combined robust least angle regression with least trimmed squares regression on jack-knife subset. When the detected outliers are removed, the standard least angle regression is applied on the cleaned data to robustly sequence the predictor variables in order of importance. [3] proposed a method called the Relative Influence Measure using the Mallow’s 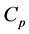 and AIC Statistics. These methods are dimensionally consistent, computationally efficient and able to identify influential case, though, failed in asymptotic consistency. [10] in comparing the BIC and AIC, stated that the AIC was not consistent. That is, as the number of observations n grows very large, the probability that AIC recovers a true low-dimensional model does not approach unity [11] . [12] supported same argument that the BIC has the advantage of being asymptotically consistent: as
and AIC Statistics. These methods are dimensionally consistent, computationally efficient and able to identify influential case, though, failed in asymptotic consistency. [10] in comparing the BIC and AIC, stated that the AIC was not consistent. That is, as the number of observations n grows very large, the probability that AIC recovers a true low-dimensional model does not approach unity [11] . [12] supported same argument that the BIC has the advantage of being asymptotically consistent: as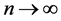 , BIC will select the correct model.
, BIC will select the correct model.
Hence, the specific objectives of this paper are to propose a relative influence measurewith an indication of whether the fit of the selected model improves or deteriorates owing to the presence of an observation (case) and that retains asymptotic consistency and hence not violating the sampling properties of the model parameters.
2. Existing Methods
2.1. Cook’s Distance and the Influence Measure
Let V be the set of indices corresponding to the predictor variables selected from the full data set and let 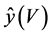 be the prediction vector based on the selected variables and calculated from the full data set. Also let
be the prediction vector based on the selected variables and calculated from the full data set. Also let  be the prediction vector based on the variables corresponding to V, but calculated from the full data set without case i. [3] noted that
be the prediction vector based on the variables corresponding to V, but calculated from the full data set without case i. [3] noted that 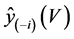 contains prediction for case i, although this case is not used in calculating
contains prediction for case i, although this case is not used in calculating . The conditional Cook’s distance for the
. The conditional Cook’s distance for the  case is
case is
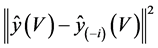 (1)
(1)
approximately scaled. Here,  denotes the Euclidean norm. Repeating the variable selection using the data without case i as pointed out by [12] , this selection yields a subset
denotes the Euclidean norm. Repeating the variable selection using the data without case i as pointed out by [12] , this selection yields a subset  of indices with
of indices with  possibly different from V. Hence, the unconditional Cook’s distance is
possibly different from V. Hence, the unconditional Cook’s distance is
 (2)
(2)
approximately scaled. Since the unconditional version explicitly takes the selection effect into account [13] argued that it is preferable. As explained in the literature, a measure say M calculated from the complete data set can as well be calculated from the reduced data set as 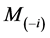 and then quantify the influence of case i in terms of a function
and then quantify the influence of case i in terms of a function  of M and
of M and . The
. The ![]() has to be based on the difference in the value of the selection criterion before and after omitting case i. This difference
has to be based on the difference in the value of the selection criterion before and after omitting case i. This difference ![]() may then be divided by M in order to calculate the relative change in the selection criterion. As proposed by [3] , the influence measure for the
may then be divided by M in order to calculate the relative change in the selection criterion. As proposed by [3] , the influence measure for the ![]() case when the Cook’s distance is used becomes
case when the Cook’s distance is used becomes
![]() (3)
(3)
2.2. Mallow’s Cp Estimate and the Influence Measure
Let Y be an ![]() vector of response in a linear regression with corresponding
vector of response in a linear regression with corresponding ![]() design matrix X of explanatory variables. A traditional model is
design matrix X of explanatory variables. A traditional model is
![]() (4)
(4)
where![]() ,
, ![]() and
and ![]() are unknown parameters. Usually,
are unknown parameters. Usually, ![]() is a
is a ![]() vector of parameters and
vector of parameters and![]() .
. ![]() often contains redundant or unimportant variables. Let RSS be the usual sum of squares from
often contains redundant or unimportant variables. Let RSS be the usual sum of squares from
the OLS fit of (4), then ![]() is the commonly used unbiased estimator of
is the commonly used unbiased estimator of![]() . Consider the subset
. Consider the subset
V of ![]() and let
and let ![]() be the residual sum of squares from the least squares fit using only the regressors corresponding to the indices in V together with an intercept. The
be the residual sum of squares from the least squares fit using only the regressors corresponding to the indices in V together with an intercept. The ![]() statistic corresponding model is
statistic corresponding model is
![]() (5)
(5)
where v is the number of indices in V. Variable selection based on (5) entails calculating ![]() for each subset of
for each subset of ![]() and selecting the variables corresponding to
and selecting the variables corresponding to![]() ; the subset minimizing (5). This approach is based on the fact that for a given V,
; the subset minimizing (5). This approach is based on the fact that for a given V, ![]() is an estimate of the expected squared error if a (multiple) linear regression function based on the variables corresponding to V is used to predict
is an estimate of the expected squared error if a (multiple) linear regression function based on the variables corresponding to V is used to predict![]() , a new (future) observation of the response random vector Y. Therefore, choosing
, a new (future) observation of the response random vector Y. Therefore, choosing ![]() to minimize (5) is equivalent to selecting the variables which minimize the estimated expected prediction error. As proposed by [3] , the influence measure for the
to minimize (5) is equivalent to selecting the variables which minimize the estimated expected prediction error. As proposed by [3] , the influence measure for the ![]() case when the
case when the ![]() criterion is used becomes
criterion is used becomes
![]() (6)
(6)
where ![]() is calculated as in (5) but with the
is calculated as in (5) but with the ![]() case omitted. In calculating
case omitted. In calculating![]() , the estimator for the error variance
, the estimator for the error variance ![]() is obtained from the full data set.
is obtained from the full data set.
2.3. The AIC Estimate and the Influence Measure
The AIC is based on the maximized log-likelihood function of the model under consideration. Suppose![]() , and ignoring constant terms, the maximized log-likelihood for the model corresponding to a sub-
, and ignoring constant terms, the maximized log-likelihood for the model corresponding to a sub-
set V is given by![]() . This is a non-decreasing function of the number of selected regressors.
. This is a non-decreasing function of the number of selected regressors.
[13] therefore included a penalty termviz;![]() , which equals the number of parameters which have to be estimated. Multiplying the resulting expression by −2 yields
, which equals the number of parameters which have to be estimated. Multiplying the resulting expression by −2 yields
![]() (7)
(7)
See [14] for details. It is known that ![]() does not perform when the number of parameters to be estimated is large compared to the sample size (typically cases where
does not perform when the number of parameters to be estimated is large compared to the sample size (typically cases where![]() . In such a case, a modified version of (7) should be
. In such a case, a modified version of (7) should be
![]() (8)
(8)
Variable selection based on (5) and (8) calculating the criterion for each subset V of ![]() and selecting the variables corresponding to the minimizing subset. This is equivalent to selecting the variables which maximize a penalized version of the maximum log-likelihood. As proposed by [3] , the influence measure for the
and selecting the variables corresponding to the minimizing subset. This is equivalent to selecting the variables which maximize a penalized version of the maximum log-likelihood. As proposed by [3] , the influence measure for the ![]() case when the AIC criterion is used becomes
case when the AIC criterion is used becomes
![]() (9)
(9)
The value of ![]() in (9) is obtained by using either (7) or (8) but with the
in (9) is obtained by using either (7) or (8) but with the ![]() case omitted.
case omitted.
2.4. The Proposed BIC-Based Relative Influence Measure
A popular alternative to AIC as proposed by [15] is the Bayesian Information Criterion (BIC) [16] - [18] .
The BIC is formally defined as
![]() (10)
(10)
![]() , where
, where ![]() are theparameter values that maximize the likelihood function. The BIC is an asymptotic result derived under the assumptions that the data distribution is in the exponential family. That is,
are theparameter values that maximize the likelihood function. The BIC is an asymptotic result derived under the assumptions that the data distribution is in the exponential family. That is,
the integral of the likelihood function ![]() times the prior probability distribution
times the prior probability distribution ![]() over the
over the
parameters ![]() of the model M for fixed observed data y is approximated as
of the model M for fixed observed data y is approximated as
![]() (11)
(11)
Under the assumption that the model errors or disturbances are independent and identically distributed according to a normal distribution and that the boundary condition that the derivative of the log likelihood with respect to the true variance is zero, this becomes (up to an additive constant, which depends only on n and not on the model).
![]() (12)
(12)
where ![]() is the error variance. The error variance in this case is defined as
is the error variance. The error variance in this case is defined as
![]() (13)
(13)
which is a biased estimator for the true variance. In terms of residual sum of squares, the BIC is defined thus
![]() (14)
(14)
The BIC is an increasing function of the error variance ![]() and an increasing function of v. That is, unexplained variations in the dependent variable and the number of explanatory variables increase the value of BIC. Hence, lower BIC implies either fewer explanatory variables, better fit or both.
and an increasing function of v. That is, unexplained variations in the dependent variable and the number of explanatory variables increase the value of BIC. Hence, lower BIC implies either fewer explanatory variables, better fit or both.
Based on (14), the proposed influence measure for the ![]() case when the BIC criterion is used becomes
case when the BIC criterion is used becomes
![]() (15)
(15)
(2.15) can take the form of
![]() (16)
(16)
Suppose![]() , by invoking trichotomy law of real numbers, (16) can be rewritten as
, by invoking trichotomy law of real numbers, (16) can be rewritten as
![]() (17)
(17)
![]()
The values of ![]() in (15, 16 and 17) are obtained by using (14) but with the
in (15, 16 and 17) are obtained by using (14) but with the ![]() case omitted. Steel and Uys (2007) claimed that influence measure can be calculated for all selection criteria where the particular criterion is a combination of some sort of goodness-of-fit measure and a penalty function (such a penalty function usually include the number of predictors of the particular selected model as one of its components [19] . Closely evaluating (14), it is clear that
case omitted. Steel and Uys (2007) claimed that influence measure can be calculated for all selection criteria where the particular criterion is a combination of some sort of goodness-of-fit measure and a penalty function (such a penalty function usually include the number of predictors of the particular selected model as one of its components [19] . Closely evaluating (14), it is clear that ![]() is a huge penalty term compared to the penalty term in (5) and (8) and hence it gives a good model fit of the data set.
is a huge penalty term compared to the penalty term in (5) and (8) and hence it gives a good model fit of the data set.
3. Results
The results above Table 1 show that the method was able to detect cases 33 and 41 as having high influence on the model given that their respective RIMs are relatively larger than others just as the AIC and Mallow’s Cp Statistic-based RIM detected. The method proposed here for simultaneously detecting influential data points and variable selection, detects outliers one at a time. However, further study can be embarked upon to detect multiple influential data points all at a time while selecting optimal predictor variables.
The problems of masking and swamping were not covered in this study. Masking occurs when one outlier is not detected because of the presence of others; swamping occurs when a non-outlier is wrongly identified owing to the effect of some hidden outliers. Therefore, further studies can be carried out to detect influential outliers and simultaneously select optimal predictor variables while incorporating the solutions to problems of masking and swamping.
![]()
Table 1. BIC-based RIM for the Evaporation data contained in [20] .
Again, because it was not intended initially to carry out a test of convergence through which we can compare the computational cost of the three methods, this work avoided the task of re-sampling which was done by Steel and Uys (2007). Meanwhile Steel and Uys (2007) did not run any test of convergence after bootstrapping rather they calculated the estimated average prediction error to substantiate their results. Hence, their additional task of re-sampling is a repetition of the results they achieved with their methods and as a result it is not necessary in this study. One can further implement these existing methods by adding a test of convergence after re-sampling.
4. Conclusion
Two things are unique about this paper namely a new approach to detecting influential outlier and then the conditions for the interpretation of the result. The later is achieved by invoking the trichotomy law of real numbers. The proposed method penalizes models hugely as the sample size becomes very large and hence has greater likelihood of choosing a better model while detecting influential data cases one at a time.