Received 17 December 2015; accepted 1 February 2016; published 5 February 2016

1. Introduction
Electromagnetic Waves are actually the radiations of Photon particles which always move in the path of wave. Photons are particles but display behavior of both particle as well as wave. The “Wave Particle Duality” is explained in this work. How actually the phenomena of Interference & Polarization take place are also explained? The mass of photon is confirmed by both Newtonian theory as well as special theory of relativity. New equations for true mass of photon according to special relativity are also derived.
Most of the particles of the size of quanta, micro & macro levels display Wave Particle Duality. Any particle can display Wave Particle Duality phenomenon and move in the form of a wave if it meets the following criteria:
- The particle has mass;
- The centre of mass of particle is different from the centre of the particle;
- The particle is spinning and moving.
Mass is a primary criterion for a particle to exhibit Wave Particle Duality. Without mass in the particle, it can neither display Wave Particle Duality nor any other phenomena like Interference & Polarization etc.
2. Discussion
PROVES OF MASS IN PHOTON
Photon is one of the tiniest particles in the universe. Being very small the mass of photons could not be measured or calculated directly. “Photon has mass” is proved by the properties and characteristics of mass exhibited by the photon. Mass of photon produces inertial force, gravitational force, angular momentum and linear momentum etc.
(a) Inertial Force Due to the Mass in Photon
Contrary to the known rule of Reflection “Angle of Reflection and the Angle of Incidence are not same but slightly different”, this difference in angle of reflection is due to the Inertial Force developed by the mass of spinning photon from within the photon.
Photons deviate from their straight line path on reflection by plain surface coated mirror due to the inertial force developed from within the photon. This inertial force increases with the increase in the angle of polarization concluding that the centre of mass and centre of photon are different. “Experimental Proof of Mass in Photon” [1] describes the details of the experiments and discovers the presence of mass in photon. This also discovers that the centre of mass of photon is different from the centre of photon. The observations of the experiments are given below:
1. The photons of polarized laser light on reflection deviate from their straight line path after reflection.
2. The angle of deviation of photons on reflection depends on the angle of plane of polarization of laser light with respect to the plane of reflecting mirror.
3. The angle of deviation increases by increasing the frequency of laser light.
4. The angle of reflection and the angle of incidence of photons are not same.
The above experiments conclude:
- Photon deviates from its straight line path due to the inertial force developed by its mass.
- Higher the angle of polarization, higher is the inertial force and higher the deviation.
- Higher the frequency, higher is the inertial force and higher the deviation.
The deviation of photons on reflection proves the followings:
1. Photon has mass.
2. The centre of mass of photon is different from the centre of photon.
Based on the “Experimental Proof of Mass in Photon” [1] , the structure of a photon is conceived as shown in Figure 1.
The centre of mass of spinning photon located at distance “r” from the centre of photon generates “Angular Momentum” which is a vector with direction changing within 360˚ with the spin of photon. The combined effect of the angular momentum and the linear momentum creates “Resultant Momentum”. The photon always moves in the direction of “Resultant Momentum” which is also a vector with direction changing within 360˚ with the spin of photon.
The “Resultant Momentum” with continuously changing direction and magnitude imparts peculiar characteristics to photon to exhibit Wave Particle Duality, Interference and Polarization etc. The experiments are based on “New Quantum Theory” [2] developed in the year 2012 hypothesizing that photon has mass and the centre of mass is located away from the centre of photon.
(b) Gravitational Force due to Mass of Photon
It is known that the photons from the different stars bend while passing near the Sun by the gravitational force between the mass of photon and the mass of the Sun.
This bending of photons proves the presence of mass in photon.
(c) Interference
![]()
Figure 1. Photon is shown in yellow circle with its centre of mass as red circle. The centre of mass of photon is located at distance “r” from the centre of photon. The direction of angular momentum is at angle “θ” from Horizontal Axis. Photon is moving in horizontal direction and spinning clockwise in vertical plane X-Z. The direction of linear momentum is constant and is in horizontal direction X-axis. The angular momentum is vector and its direction keeps on changing continuously with the spin of photon within 360˚. The direction of Resultant Momentum is ϕ from the horizontal direction X-axis and also keeps on changing continuously with spin of photon within 360˚.
1. Constructive Interference
In constructive interference two monochromatic electromagnetic waves are either in same phase or in multiple phase of 2π. The photons of both waves superpose and behave as one due to coalescing effect. The superposed photons with their centre of mass and angular momentums are shown in Figure 2.
Since both the photons are in the same phase, their angular momentums are added to double. This results in double amplitude at the crests and troughs with maximum brightness.
2. Destructive Interference
In destructive interference the two monochromatic electromagnetic waves are in phase difference of odd multiple of π. The photons of both waves superpose and behave as one due to coalescing effect. The superposed photons with their centre of mass and angular momentums are shown in Figure 3.
Since both the photons are in the opposite phases, both the centre of mass are located at 180˚ from each other. The angular momentums of both photons are always in the opposite directions. Both the coalesced photons though keep on spinning but cannot go up & down to form wave and move only in the straight line. This results in destructive interference with minimum brightness.
3. Interference with Other Phase Differences
When two monochromatic electromagnetic waves, with phase difference other than 0˚ or multiple of π intersect, the photons of both superpose each other with coalescing effect. Depending on phase difference of the two photons, both the centre of mass are located at different positions with angular momentums in different directions as shown in Figure 4(a) & Figure 4(b).
The angular momentums of both the photons are in different directions and the vector sum of both the angular momentums is the resultant angular momentum. Such interference results in intermediate brightness between minimum to maximum.
The Interference phenomenon can only take place if the photons have mass and the centre of mass is different from the centre of photon. The Interference phenomenon is not possible without the mass in photon.
The phenomenon of interference proves that photon has mass and the centre of mass is different from the centre of photon.
(d) Polarization
On polarization of electromagnetic radiations, the photons form wave in one plane only known as the plane of polarization. The photons spin and move in the plane of polarization only. Figure 5 shows a polarized photon with its centre of mass and the circular path of movement of centre mass with the spin of photon.
![]()
Figure 2. The angular momentums of both photons are in the same phase and added to double.
![]()
Figure 3. Both the photons in phase difference of π have centre of mass located at 180˚ apart. The directions of angular momentums of both are opposite to each other.
![]()
![]() (a) (b)
(a) (b)
Figure 4. (a) With phase difference closer to 0˚, both the centres of mass are close to each other with their angular momentums. Therefore the vector sum of both angular momentums is more and the brightness is on higher side; (b) With phase difference closer to π, both the centres of mass are away with angular momentums closer to opposite direction. Therefore the vector sum of both angular momentums is less and the brightness is on lower side.
The direction of angular momentum originating from the centre of mass of photon keeps on rotating with the centre of mass and changes its direction within 360˚ within the plane of polarization only. The direction of resultant momentum which is the vector sum of angular momentum and the linear momentum also changes its direction within 360˚ in the same plane. The resultant momentum moves the photon up and down in the plane of polarization and limits the photon movements forming the wave in one plane only.
The polarization phenomenon can only take place if photon has mass and the centre of mass is different from the centre of photon. The polarization phenomenon is not possible without the mass in photon.
![]()
Figure 5. Centre of Mass of photon rotates in circular path with the spin of photon in the plane of polarization. This changes the direction of angular momentum continuously within 360˚ angle. The resultant momentum due to angular momentum & linear momentum moves the photon up & down in X?Z plane of polarization to form the wave.
The phenomenon of polarization proves that a photon has mass and the centre of mass is different from the centre of photon.
3. Mass of Photon by Special Relativity
The special theory of relativity correlates energy, mass, momentum, velocity from the observer’s frame of reference.
Since a photon is never at rest, the mass of photon (the matter in the photon) can be called “True Mass of photon (mt)” instead of rest mass (m0). True mass of a photon is always constant irrespective of the position of the observer. For a single photon particle, the rest mass and the invariant mass are the same.
A. True Mass of Photon from Total Energy of Photon
The equation 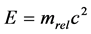 of special relativity is used to derive new equation for the True Mass of photon (mt) as under:
of special relativity is used to derive new equation for the True Mass of photon (mt) as under:
The E of the above equation specifies the “Total Energy (E)” of Photon. This includes the energy in all the physical forms possessed by the photon plus the energy produced when the mass of photon is also converted to the energy.
Photon is always spinning and moving with velocity of light. A photon as per Figure 1 is considered to calculate the total energy and True mass of the photon.
- 
- Kinetic Energy of photon: 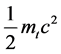
- Rotational Kinetic Energy of photon: 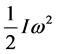
- Energy by conversion of Mass of photon: 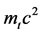
- Total Energy of photon 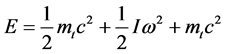
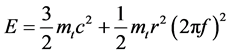
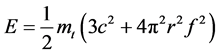
Or True Mass of Photon
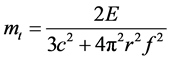 (1)
(1)
B. True Mass of Photon from the Momentum of Photon
According to the special relativity, the total energy of photon is specified by the following equation:
![]() (True mass mt is used instead of m0)
(True mass mt is used instead of m0)
For a photon, true mass (mt) and linear velocity (c) are always constant. But in the term (pc) both the momentum (p) and the instantaneous tangential velocity of photon in the curve path of wave are vectors and variable in one cycle of wave. Considering the direction of Resultant Momentum is (ϕ) from the X-axis, the resultant momentum of photon is denoted as (pϕ) and the velocity of photon (cϕ) in the curve path of wave. The above equation is rewritten as under:
![]()
From Figure 1, the centre of mass of photon is at a distance (r) from the centre of photon. The photon is always spinning and moving in the path of wave. The equation for True mass of photon (mt) can be derived by calculating the Resultant Momentum (pϕ) of photon at any spin position/position of curve path of wave as under:
- ![]()
- ![]()
- ![]()
- ![]()
- ![]()
- Magnitude of Resultant Momentum of photon (pϕ) (when the direction of angular momentum is (θ) from horizontal axis)
![]()
Or
![]()
Or
![]()
The direction of resultant momentum (ϕ) from horizontal X-axis is given below:
![]()
Substituting the value of resultant momentum (pϕ) in the total energy equation:
![]()
True mass of photon
![]() (2)
(2)
Both the linear momentum and the angular momentum account for the True mass of photon and the momentum can be used to calculate the true mass of photon.
Above mentioned two new equations provide new tools to calculate true mass of photon if some more information of the photon can be explored.
C. Relation between Mass & Momentum of Photon
“Momentum can exist without mass in photon” is a misconception and explained here.
Whereas The total energy (E) of photon (particle) includes all physical forms of energy possessed by the photon plus the energy produced by the true mass of photon by the equation![]() , the energy (e), according to the Planck-Einstein equation e = hf specifies only all the physical forms of energy possessed by the photon. This (e) does not include the energy produced if the true mass of photon is converted to energy.
, the energy (e), according to the Planck-Einstein equation e = hf specifies only all the physical forms of energy possessed by the photon. This (e) does not include the energy produced if the true mass of photon is converted to energy.
The special theory of relativity specifies the total energy of photon by the following equation:
![]() (True mass mt is considered instead of m0)
(True mass mt is considered instead of m0)
In the above equation the term (pc) relates to the average values of momentum & velocity of photon in one complete cycle of wave. When the mass of photon (mt) is assumed to be zero in the above equation, the (E) of the above equation changes to (e) as under:
![]()
The Planck-Einstein equation specifies the energy (e), all physical forms of energy possessed by the photon only without the energy produced by the conversion of true mass of photon to energy.
![]()
Or ![]()
Or momentum ![]()
In both the above mentioned equations (Planck-Einstein equation and Special Relativity), the true mass (mt) of the photon has been totally ignored. The relation between momentum and frequency is derived without considering the mass of photon. It is presumed that the momentum can exist without the mass in photon, which is not correct. Only the mass/matter produces momentum in a particle.
Energy cannot exist in isolation without mass. There has to be mass (matter) to possess any form of energy.
Both Newtonian theory as well as special theory of relativity confirms that photon has mass.
where
- mt: True Mass of photon;
- c: Linear velocity of photon in X-direction;
- cϕ: Tangential velocity of photon in curve path of wave when the direction of resultant momentum is at angle ϕ from X-axis;
- I: Moment of Inertia of photon;
- ω: Angular velocity of photon;
- ƒ: frequency of photon;
- r: Distance of centre of mass of photon from the centre of photon;
- p: Average resultant momentum of photon in one cycle of wave;
- pϕ: Resultant momentum of photon when the direction of resultant momentum is at angle ϕ from X-axis;
- h: Planck’s constant;
- θ: Angle of Angular Momentum from X-axis;
- ϕ: Angle of Resultant Momentum from X-axis;
- E: Total energy possessed by photon including energy by conversion of mass of photon to energy;
- e: Energy possessed by photon excluding the energy by conversion of mass of photon to energy.
4. Example of Mass of Photon
An example of Photoelectric effect conserving the mass of photon is given below:
A photon hits a free electron in PV cell and combines with electron. The photon transfers its energy (e = hf) to the electron. The combined energy of photon and electron ejects the electron (along with photon). The mass of photon is not converted to energy and remains as such since there is no reaction to convert mass into energy. This electron travels to a LED bulb which emits out a new photon with its mass (frequency of photon depends on type of LED). From LED bulb the electron returns to PV cell.
In the above example the mass of photon remains as such and only the transfer of energy takes place.
5. Wave Formation by Photon
“Experimental Proof of Mass in Photon” [1] discovers that photon has mass and its centre of mass is different from the centre of photon. This discovery of mass is further supported by the various facts, the Newtonian theory and special theory of relativity. How a particle of photon forms wave by virtue of its mass is explained here?
A moving photon spins around its own centre. The centre of mass of photon, located at a distance “r” from the centre of photon, rotates in a circular path of radius “r” within the photon. The mass of photon develops angular momentum originating from the centre of mass in direction perpendicular to the radial line from centre of photon to the centre of mass. With the spin of photon, the direction of angular momentum keeps on changing continuously from 0˚ to 360˚. The direction of linear momentum of photon is always constant. Figure 6 shows the directions of angular momentums at intervals of 45˚ in one revolution of photon.
The mass of a spinning photon develops angular momentum from within the photon of continuously changing direction. This angular momentum and linear momentum develops resultant momentum of continuously changing direction within 360˚ also from within the photon. “Resultant Momentum” is the vector sum of both the linear momentum and the angular momentum. The magnitude (pϕ) and the direction (cϕ) of the resultant momentum at any position of curve path of wave have been already calculated above.
The direction of resultant momentum (ϕ) changes within 360˚ with the spin of photon and is also the direction of the photon in the curve path of wave. The formation of wave is explained below step by step:
- The photon moves continuously in X-direction (direction of travel) due to the linear momentum (mt c) which always remains in X-direction.
- During the 1st quarter of wave formation (position 1 to 3) as the photon spins, the centre of mass rotates and the direction of resultant momentum keeps on changing continuously from position 1 to position 3 (horizontal X-direction) as shown in Figure 7. During this 1st quarter movement, the photon moves in X-Z direction upward to the crest position of the wave by its resultant momentum. The upward movement of photon both in X & Z directions simultaneously forms the wave of the 1st quarter as shown in Figure 7.
- During the 2nd quarter of wave formation (position 3 to 5) as the photon spins, the centre of mass rotates and the direction of resultant momentum keeps on changing continuously from position 3 to position 5 as shown in Figure 7. During this 2nd quarter movement, the photon moves in X-Z direction downward to the position 5 of the wave by its resultant momentum. The downward movement of photon both in X & Z directions simultaneously forms the wave of the 2nd quarter as shown in Figure 7.
![]()
Figure 6. The direction of linear momentum is constant, whereas the direction of angular momentum keeps on changing continuously with the rotation of photon along with its centre of mass. The directions of angular momentums starting from 0˚ are shown at intervals of 45˚. The angular momentum/resultant momentum moves the photon up and down continuously to form wave.
![]()
Figure 7. As the photon spins the centre of mass rotates. The direction of the resultant momentum changes continuously to move the photon up & down to form wave.
- During the 3rd quarter of wave formation (position 5 to 7) as the photon spins, the centre of mass rotates and the direction of resultant momentum keeps on changing continuously from position 5 to position 7 (horizontal X-direction) as shown in Figure 7. During this 3rd quarter movement, the photon moves in X-Z direction downward to the trough position of the wave by its resultant momentum. The downward movement of photon both in X & Z directions simultaneously forms the wave of the 3rd quarter as shown in Figure 7.
- During the 4th quarter of wave formation (position 7 to 1 of the next wave cycle) as the photon spins, the centre of mass rotates and the direction of resultant momentum keeps on changing continuously from position 7 to position 1 of the next wave cycle as shown in Figure 7. During this 4th quarter movement, the photon moves in X-Z direction upward to the position 1 of the next wave cycle by its resultant momentum. The upward movement of photon both in X & Z directions simultaneously forms the wave of the 4th quarter as shown in Figure 7.
- With every cycle or spin of photon the above process is repeated to form electromagnetic wave by the particle of photon.
All elementary particles display Wave Particle Duality as explained above. This also explains how any spinning particle with centre of mass being different from the centre of particle always moves in the path of wave.
A spinning spherical particle of uniformly distributed mass moves in straight line. Similarly a spinning spherical particle having mass located in the centre of the particle also moves in the straight line. Whereas spinning spherical particle with centre of mass which is not in the centre of particle moves in the path of wave.
If the plane of spin of centre of mass of photon is different from the direction of travel of photon, wave in all 3 dimensional is formed.
6. Conclusions
A spinning photon develops resultant momentum from inside due to the mass of photon with centre of mass different from the centre of photon. The resultant momentum moves the photon particle in the path of a wave and explains Wave Particle Duality.
The angular momentum of photon due to the mass of photon explains all different types of Interference phenomena and also the Polarization phenomena.
The phenomena like Wave Particle Duality, Interference and Polarization displayed by the elementary particles including photons are only possible with the presence of mass in the particles with centre of mass different from the centre of the particles.
The mass of photon explains Wave Particle Duality, Interference and Polarization phenomena to supplement the Quantum Theory.