Received 28 December 2015; accepted 26 January 2016; published 29 January 2016
1. Introduction
Can the existence of “God” be determined purely from scientific and mathematical considerations? Before we can even discuss such a question, we are confronted by which definition of God shall be applied in our discussion. Compounding the problem are the many personal beliefs that will inevitably resist scientific explanations and descriptions of God. This includes, the devout, the atheist or otherwise. The difficulty then, is not the science. It is our social and religious perception on the limits of science.
Because this is a scientific paper (and not a theological one), the god we are seeking will be that of Spinoza and Einstein―where the Universe is thought to be identical with divinity. As Einstein expressed about God [1] :
“My views are near those of Spinoza: admiration for the beauty of and belief in the logical simplicity of the order which we can grasp humbly and only imperfectly. I believe that we have to content ourselves with our imperfect knowledge and understanding and treat values and moral obligations as a purely human problem―the most important of all human problems.”
And since we seek the god of Einstein, if we are to have even a modicum of success at affirming the existence and properties of “God”, it will be most advantageous to follow the traditions of science, rather than the modality of theology―which cogitates upon those morals and ethics as mandated by their personal God. Though morality and ethics play a necessary cultural role in space and time, they have no place in spacetime.
2. The Increments of Memory and Consciousness
By what scientific methodology shall we determine the properties of the god of spacetime? It will be done by what we refer to as increments―succinct hypotheses that are to be verified through empirical evidence. This incremental-empirical approach is juxtaposed to those elegant arguments and double meanings propounded by such great theologians and philosophers as:
Teilhard de Chardin [2] : “Someday, after mastering the winds, the waves, the tides and gravity, we shall harness for God the energies of love, and then, for a second time in the history of the world, man will have discovered fire.”
The philosopher Alfred North Whitehead who says [3] [4] : “The Church gave unto God the attributes which belonged exclusively to Caesar.” And his challenge to science: “… scientific cosmology which presupposes the ultimate fact of an irreducible brute matter, or material, spread through space in a flux of configurations. In itself such a material is senseless, valueless, purposeless. It just does what it does do, following a fixed routine imposed by external relations which do not spring from the nature of its being. It is this assumption that I call ‘scientific materialism.’ Also it is an assumption which I shall challenge as being entirely unsuited to the scientific situation at which we have now arrived.”
And the French philosopher Henri Bergson [5] : “Perception is the master of space in the exact measure in which action is the master of time.” As he states in the third chapter of Matter and Memory: “If you abolish my consciousness… matter resolves itself into numberless vibrations, all linked together in uninterrupted continuity, all bound up with each other, and traveling in every direction like shivers.” Bergson’s attempt to relate matter with memory follows closer to what we will argue for in this paper.
3. Properties of God
If we are to succeed with our incremental investigation into the spacetime properties of god, it will be necessary to define our objective in a clear and straightforward manner, and do so by limiting our deliberations into solvable increments. Such an incremental approach has the advantage of being deterministic, comprehensible, and beautiful in its elemental form. It is differentiated from the all-in-one approach, which is poetic, uncertain, yet essential to our humanity.
To carry out the incremental approach, succinct propositions will be presented and subjected to scientific evaluation. Should any such increment fail scrutiny―including the empirical test―we must reject said increment. If all increments fail, then in the limit, we reject the existence of a spacetime god-universe. If, on the other hand, we are able to determine even a single valid increment, then increment-by-valid-increment we have a methodology for constructing a model of god―the Grand Observer of spacetime.
It must be stated, because we are investigating the god of Spinoza and Einstein―where the universe is equivalent to divinity, then, by simple observation of planets, stars and galaxies …, we can assert empirically that god exists. And since we exist in spacetime, we also know memory, consciousness and feelings are aspects of the god-universe. In this limited sense, we have just argued spacetime manifests the properties of memory, consciousness and emotion. However, what we wish to ascertain about spacetime, is far less obvious, far more subtle―we seek to know if spacetime itself exhibits the properties of memory and consciousness. To answer such a question―antipodal to the space and time of memetics [6] , but not necessarily to Carl Jung’s collective unconsciousness and his archetypes [7] transposed into spacetime and his ideas of synchronicity arising in conjunction with the eminent physicist Wolfgang Pauli―we begin by stating two founding propositions (increments):
1) Memory, consciousness and choice are fundamental properties of spacetime processes.
2) Since we have accepted god to be identical with the universe, and by the first proposition (memory, consciousness and choice are properties of spacetime), this meets the criteria for the god-universe of Spinoza and Einstein, but with the added property of “awareness.”Awareness is defined to be the combination of memory and conscious choice integral to some entity.
4. The Methodology to Memory and Consciousness
How then do we go about showing that memory, consciousness and choice are fundamental properties of spacetime? Through a three-fold program:
1) Our starting point begins with an 1867 letter written by James Clerk Maxwell to Peter Guthrie Tait [8] , in which Maxwell sets up a thought experiment to violate the Second Law of Thermodynamics. Borrowing from Maxwell, we apply the essence of his thought experiment to the core of the Milky Way Galaxy (or any other spiral galaxy). Then applying the aforementioned ideas of Maxwell and Leó Szilárd [9] , we argue the spacetime processes occurring within the galactic core are such, that they violate the Second Law of Thermodynamics―or would have, if it were not for the positive entropy gain resulting from the spacetime’s measurement and flipping of excited gravitons from attractive to repulsive―analogous to “Maxwell’s Demon” sorting fast and slow gas molecules and then opening the valve to segregate them into different chambers.
2) The mathematics and physics applied in our discussions will be that of General Relativity―from which two mass generators are calculated from a modified flat-spacetime metric describing graviton oscillations caused by vacuum energy fluctuations. Operating on the extreme spacetime within the galactic core (with these two mass-generators), yields the Higgs boson mass. The associated coupled general relativistic wave equation to spin-0 particles, yields the spin of this so called God-Particle [10] . In addition to general relativity, we will also present some limited thermodynamical mathematics.
3) Finally, we will show that spacetime memory and consciousness can be verified empirically. This we do by relating spacetime consciousness and memory to graviton excitement and decay (resulting in the production of a matter cocoon permeating our Milky Way Galaxy), to measurable galactic affects, such as constant rotation curves [11] , as well as accelerated spacetimes [12] .
5. Maxwell’s thought Experiment
What exactly is Maxwell’s thought experiment? Simply put, Maxwell envisaged two chambers filled with the same gas at thermal equilibrium with each other―meaning both chambers were at the same temperature and pressure (among other things). Maxwell further imagined a valve (placed between the two chambers) that could be opened or closed at the discretion of an intelligent creature who stood watch over all the moving gas molecules. Maxwell understood not all gas molecules moved at the same exact speed―statistically some gas molecules would move slower than others, some faster; it’s just the way nature worked. It was the task of Maxwell’s intelligent creature to open the valve when a fast moving gas molecule approached, so as to allow it to pass into the adjoining chamber of fast gas molecules. Likewise, as slow gas molecule neared the valve, the creature opened the valve to let it pass into the chamber of slow gas molecules; otherwise the valve would remain shut sealing off both chambers from each other. In this way a build-up of faster molecules would favor one chamber, and slower molecules favor the other chamber. The final outcome―a temperature and pressure difference between the two chambers. Since this difference could be exploited by a pneumatic motor or heat engine, to do work for free, and the process of separating fast and slow gas molecules could be done at infinitum, in effect Maxwell had presented the world with a perpetual machine―a clear violation of the Second Law of Thermodynamics. Since James Clerk Maxwell was of equal stature to Sir Isaac Newton in the science world (and later Albert Einstein to Maxwell), and that the Second Law was assumed to be fundamental to nature, and had been empirically verified to be so―yet Maxwell’s thought experiment suggested otherwise―this posed a great puzzle to the scientific community.
Fast forward eighty or so years, to when Leó Szilárd discovered a way to overcome Maxwell great puzzle. This Szilárd did in his 1929 paper [13] [14] , in which he showed entropy S (associated with information and memory) was and equal to:
(1)
where k is Boltzmann’s constant. Though C. E. Shannon is often considered to be the “Father of Information Theory” [15] , the preceding equation is considered by many to make Szilárd the originator of information theory. The proposed idea by Szilárd―that the intelligent creature (later referred to as Maxwell’s Demon) determines which molecule is faster or slower, requires a gain in information (memory) by the creature, as quantitatively expressed by Equation (1) above. In effect, a bit of information gain compensates for entropy loss of the system (of gas) during Maxwell’s Demon separating fast and slow gas molecules. Thus, Szilárd had found a way to preserve the Second Law of Thermodynamics.
As Szilárd best expresses his own solution to Maxwell’s thought experiment (and we shall similarly follow in ours):
“The objective of the investigation is to find the conditions which apparently allow the construction of a perpetual-motion machine of the second kind, if one permits an intelligent being to intervene in a thermodynamic system. When such beings make measurements, they make the system behave in a manner distinctly different from the way a mechanical system behaves when left to itself. What we show that it is a sort of a memory faculty, manifested by a system where measurements occur, that might cause a permanent decrease of entropy and thus a violation of the Second Law of Thermodynamics, were it not for the fact that the measurements themselves are necessarily accompanied by a production of entropy.”
By analogy to Maxwell-Szilárd approach, we will argue that extreme spacetimes create similar circumstances that invoke spacetime properties of memory and conscious choice. But does the Maxwell-Szilárd approach have any real support within the scientific community? The answer is a resounding yes. What ensued over the next hundred and fifty years after Maxwell wrote his letter to Tait, was an impressive list of scientists and mathematicians who proposed their own unique rebuttal or support of the Second Law. These include such scientific luminaries as: W. Thomson (Lord Kelvin) [16] ; J. Poincare [17] ; M. Planck [18] ; L. Szilárd [19] [20] ; J. von Neumann [21] ; G. Gamow [22] ; M. Born [23] ; N. Wiener [24] ; D. Bohm [25] ; L. Brillouin [26] ; M. N. Saha [27] ; R. Feynman [28] ; Bell [29] ; K. R. Popper [30] ; C. H. Bennett [31] ; S. W. Hawking [32] ; R. Landauer [33] ; R. Penrose [34] ; W. J. Christensen Jr. [35] [36] and many others.
It is with Maxwell-Szilárd’s ideas we now argue, in a rudimentary, yet scientific way, that spacetime itself has the property of memory and conscious choice.
6. Cosmological Prototype for Spacetime Consciousness and Memory
In 1988, Sir Roger Penrose shared the Wolf prize with Stephen Hawking for their contribution to our understanding of the universe. Subsequently, in 2011, Penrose wrote an article with Dr. S. Hameroff (in which I participated in that special edition on consciousness to which Penrose was also the special guest editor) [37] [38] . In their article, Penrose and Hameroff stated:
“The nature of consciousness, its occurrence in the brain, and its ultimate place in the universe are unknown.”
In reply to Penrose and Hameroff, it will be the focus of this paper to offer a cosmological prototype for the origin of consciousness and memory originating from spacetime itself [39] . “Spacetime-Thinks” begins with an analogous Maxwell-Demon model applied to the spacetime physics occurring within the core of the Milky Way Galaxy (or to any other spiral galaxy). Within this region of extreme spacetime we had argued in our previous papers [40] [41] ―through a relativized quantum physics approach (RQP)―that gravitons can be excited in the galactic core to higher energy states (for the purposes of understanding, gravitons can be thought of astiny vibrating spheres of pure geometry filled with gravitational energy, which can be excited into higher n and n2 energy states). Excited gravitons have the further property that when they decay two things occur: If gravitons have the correct n-value or n2 excited state value, or combination of both, their released gravitational energy will be absorbed by the vacuum energy to produce Standard Model particles, including the Higg’s boson―popularly referred to as the God Particle―which was recently discovered at CERN (though, under somewhat less than chary circumstances) [42] . If the graviton is at the incorrect excited n-valued state, the released gravitational energy will not be absorbed by the vacuum energy, but instead flows on like dark light causing accelerated spacetimes.
But how do such spacetime processes empirically support galactic memory and consciousness under a Maxwell-Szilard spacetime model? The quick answer is through the random sign flipping of gravitons from attractive to repulsive―equivalent to spacetime information acquisition (sorting measurement) and choice to flip the graviton sign from attractive to repulsive (a measurable bit of work-information k ln2).
7. Graviton Excitement and Decay
Rather than reproducing those general relativistic calculations carried out in our aforementioned papers―in which the precise energy levels of excited gravitons were calculated from the mass generators, we now provide a logical argument for graviton excitement and decay based on the well-established principle of Occam’s Razor. To do so, we argue that dark matter and dark energy are tantamount to graviton state processes. Furthermore, by equating the two, it allows us to go from hypothesis and empirical measurements to the conclusion that “Spacetime Thinks.” The argument is as follows:
1) Though it is possible that dark matter and dark energy are actually something other than matter and energy, by Occam’s razor we reject all other complicating possibilities. Similarly, we reject any explanations for dark matter and dark energy that lies outside the scope of quantum field theory or general relativity―such an inquiry would go beyond known physics and result in many unnecessary complications, uncertainties and absurdities. Moreover, by Occam’s razor, we shall not complicate matters by considering exotic particles extraneous to these two well-established theories of Nature.
2) Since dark matter is connected strongly to galactic mechanics in various observed ways [43] -[55] , and in particular with constant rotation curves [56] [57] , we assume dark matter and dark energy arise out of galactic spacetime processes [58] [59] . Furthermore, we argue that these spacetime processes are extreme enough to excite dark matter into higher energy states [60] [61] . If dark matter can be excited into higher energy states [62] [63] , then it is reasonable to expect dark matter can decay back into lower energy states [64] -[67] .
3) Since dark matter seems to act only gravitationally on matter, and that gravitons are the only particles associated with gravitational force and energy, then it must be that dark matter is comprised of mostly of gravitons [68] , that we have argued can be excited in higher energy states.
4) Because we have assumed that dark energy is not some exotic form of energy, and that dark energy is given that name for obvious reasons, and so cannot be electromagnetic radiation―which interacts differently with matter [69] , we conclude dark energy can only be gravitational energy [70] -[76] , which acts only gravitationally on matter, as observed by accelerated spacetimes [77] .
5) Since gravity, as described by general relativity, is a geometric-energy-matter theory, and that in 1939 M. Fierz and W. Pauli gave it a particle interpretation―as did many significant physicists, such as R. Feynman [78] -[88] , it follows from the duality of gravity as geometry and particles and that spacetime can be warped― that within extreme regions such as galactic core where a black hole resides―that spacetime itself can be compressed into geometric-particles called gravitons, which can be excited into higher states [89] -[93] .
6) Since dark matter effects are also observed outside the galactic core [94] -[99] , and that we have argued dark matter is comprised essentially of excited gravitons, then nature must provide some exceptional mechanism for gravitons to leave the galactic core; a region of spacetime where gravitational pull is so strong no light may escape. This is only possible if said gravitons switch sign from attractive to repulsive, thereby causing them to accelerate away and stream-out from the galactic core, to form a kind of Gaussian graviton-flux [100] -[105] .
7) Since the above-mentioned galactic processes are supported by the empirical evidence of a spherically symmetric dark halo permeating all spiral galaxies [106] -[110] , we conclude energetic gravitons exiting the galactic core at near the speed of light [111] -[115] , must decay so as to slow down to form as spherically symmetric dark matter halo. Eventually these excited gravitons decay to ground state and become massless [116] [117] . Thus our approach is both a massive and massless theory of gravity.
8) For excited gravitons to flux out of the galactic core, some physical process is required to switch gravitons from attractive to repulsive. Since by preceding arguments, we argue spacetime “itself” makes a graviton sign-measurement (memory). If the graviton is attractive, spacetime switches the graviton sign from attractive to repulsive (conscious choice). Outside the galactic core spacetime switches the excited graviton from repulsive back to attractive, and the graviton decays by releasing gravitational energy. This parallels Maxwell’s Demon measuring fast and slow gas molecules, storing graviton information so it could then select which gas molecules are to be allowed to pass from one chamber into the other chamber of gas molecules. In our case it is spacetime itself that chooses which graviton will have its sign switched. This collective spacetime process is tantamount to Einstein’s universe-god, with the additional attribute of awareness.
8. Hooft-Veltman Particles
The purpose of this section is to correlate graviton sign-switching to the creation of particle mass and spin generated from gravitational energy release into the vacuum energy. To do this, we supply our general relativistic results (developed in our previous papers), which allows us to calculate both the particle’s emergent mass and spin from the vacuum energy. Hence, we will have a general relativistic representation of “Spacetime Thinks.”
The particular particle we choose to represent this process of mass-spin correlated with spacetime memory and conscious choice―is the God Particle or spin-0 Higgs boson. Our first step is to write out a fully covariant expression of spin-2 particles interacting with spin-0 particle:
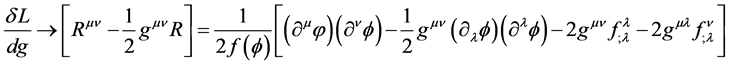(2)
For the second step, we consider a flat spacetime region free of spin-0 particles. This allows us to shut off the right side of the equation, which we may now set to zero. This further allows us to recalculate the covariant and contravariant energy momentum tensors in flat spacetime―but to do so at the microscopic level― where vacuum energy fluctuations induce graviton vibrations. The Minkowski metric cannot be applied to a chaotic vacuum energy causing graviton oscillations; instead we need a new kind of flat-spacetime metric that describes graviton oscillation, which the author developed in his previous papers:
(3)
Acting upon this modified flat-spacetime metric with the general relativistic wave equations, results in a pair of n-valued covariant and contravariant energy momentum tensors―analogous to quantum raising and lower operators [118] :
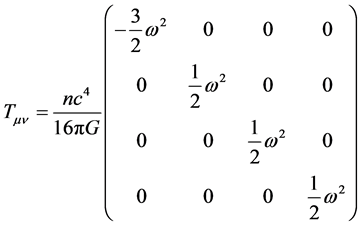(4)
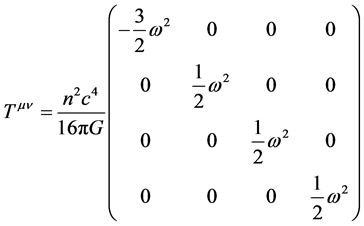(5)
Without losing structural integrity, we assume these energy momentum tensors can be detached from the general relativistic wave equations and moved to a region of spacetime rich in spin-0 particles. By “detaching” we literally mean to separate the contravariant and covariant energy tensors completely from the Einstein wave equation, to then treat them like raising and lowering operators acting on extreme spacetime―where the more dynamic the spacetime (center of galaxies), the larger the value of “n” or “n2” will be generated, and correspondingly the larger Standard Model particle masses will be created out of the vacuum energy. In practice, galactic probes would be calibrated to measure the mass-energy calculated from these two tensors.
Now that the right hand side of the Equation (2) has been fully developed in flat spacetime (and in such a way that the energy momentum tensors can be detached and “transported” into curved spacetime), it allows us to now turn back to the left-hand-side of the equation containing the spin description of the particle we are interested in. Since in this paper we are seeking the Higgs boson, or god particle, we may now rewrite Equation (2)― relating boson spin to boson mass, as:
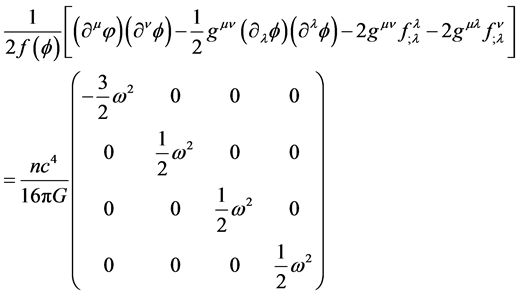(6)
Contravariant spin-energy expression, as:
(7)
What these mathematical equations represent, are graviton excitement and the spacetime processes of memory and conscious choice. In the next section we will relate these equations to the Higgs boson.
In closing this section, we note that the covariant and contravariant energy momentum tensors are related via raising and lowering properties of the spacetime metric:
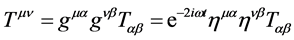(8)
Since the covariant tensor is completely real, whereas the contravariant tensor complex, (each contributing to fundamental particle mass), and since both tensors are acting on the same point in spacetime, this suggests a superposition principle for spacetime itself. Moreover, it offers an explanation as to why ordinary matter dominates in the universe. Finally, we note that the two energy tensors obey conservation of energy:
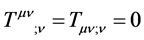(9)
Physically this implies the resulting general relativistic energy momentum tensors are consistent and valid, in the same way as were the electromagnetic equations made consistent, (and a correct and beautiful expression of nature), after James Clerk Maxwell added a single term to Amperes’ law. It further brings validation to space- time memory and consciousness fundamental extreme spacetime processes.
9. Boson Mass Calculations (God particle)
Though part of this section was developed in our previous paper, its application was limited to Standard Model mass determination. Here we apply that work in a new and unique way to demonstrate that memory and consciousness are fundamental properties of spacetime―in particular, that excited graviton switching from attractive to repulsive, shows spacetime behaves in a Maxwell-Szilárd mode. Furthermore, that the following mathematical calculations derived from the detached energy momentum tensors―turned into mass generators, provides the numbers so that spacetime awareness can beempirically verified by building galactic probes sensitive to these numbers. Hence we provide both the mathematics and scientific evidence that “God” is verified through the spacetime creation of the God-Particle.
We now calculate Higg’s boson (God Particle) mass from the detached covariant and contravariant energy momentum tensors turned into mass generators. We begin through evaluation of the time component of the general relativistic energy momentum operators:
(10)
From the covariant and contravariant energy momentum tensors, and number density of particles approximated in extreme spacetimes (near black holes), we calculate the energy per particle:
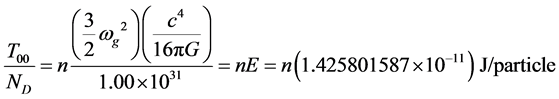, (11)
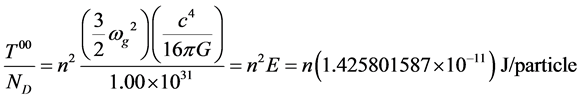(12)
where 
is the graviton angular frequency calculated in our precursor paper:
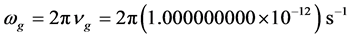(13)
With 
and![]()
. This is the base energy in the creation of both the mass and spin of a particle formulated from the General Theory of Relativity. By dividing this energy by Planck’s constant will provide us with the energy-to-spin ratio necessary to not only generate mass but the spin of all particles (including spin-0 Higgs particle.
![]()
(14)
This is the fundamental spin-mass frequency required to generate massive particles from excited gravitons releasing their gravitational energy into the vacuum energy. This associated wavelength is:
![]()
(15)
Next we convert the energy operators T00 into mass generators:
![]()
(16)
![]()
(17)
Finally, we compute the Higgs (or rather Hooft-Veltman) boson mass by selecting n = 32 for the covariant contribution, and n = 37 for the contravariant mass contribution:
![]()
(18)
The contravariant mass contribution is given by:
![]()
(19)
Combining these two masses via superposition of the two energy operators, we determine the theoretical mass value for the Higgs-boson:
![]()
(20)
The mass result for the Higgs particle is in precise agreement that reported by CERN 2.246153925 × 10−25 kg.
Just as Schrodinger’s equation produced n-valued energy states, so to do the mass generators produce n-valued graviton states leading to Higgs mass and other Standard Model particle mass. We refer to the collection of all Standard Model particles produced during graviton excitement and decay into the vacuum energy, as Hooft-Veltman particles.
10. Galactic Memory and Consciousness
So far we have argued that graviton excitation is a natural consequence of the galactic spacetime dynamics. Moreover, these galactic processes involve spacetime information acquisition and graviton sign-switching. Since these processes were argued to be analogous to the Maxwell-Szilárd thought experiment in preserving the Second Law of Thermodynamics through information acquisition and sorting of gas molecules, this implies “Spacetime Thinks.”
The question that we consider now, is: Should these galactic processes go on at infinitum (the old galaxies die off, new ones are born), is spacetime able to store the process of sign switching at infinitum, or would it be necessary for spacetime to undergo memory erasure―as Charles Bennet proposed for Maxwell’s Demon? We argue that in four-dimensional spacetime, it is not necessary for spacetime memory erasure to store an infinite amount information, or even a bigger infinity of information.
To show this we note gravitons are discrete entities and so countable. Since we also showed graviton excitement levels are n-valued―(either n-valued or n2-valued, or a combination of both), this means the spacetime process of information acquisition, and graviton sign switching (of all gravitons), is collectively countable. This further implies we may establish a one-to-one correspondence between graviton processes and the natural numbers {N}. Whether there are ten gravitons, ten billion gravitons, or even an arbitrarily large number of these geometric particles, nevertheless memory acquisition and sign switching is countable and can be represented by the infinite set of natural numbers {N}. However, since spacetime must be described by the set of real numbers r3, which are a subset of the larger infinite set of complex numbers C, this further implies spacetime can always store, at infinitum, all galactic information processes―including those that might require the set of real numbers R―and do so without the need for memory erasure.
To understand this storage mathematically, consider the closed interval between the numbers one and two [1] [2] (each natural number representing an excited graviton). In this interval, there are exactly two natural counting numbers, i.e. the number one and the number two. Whereas in the same interval there is uncountable many real numbers; for example![]()
, π/2 …. What this implies is that, even though the set of natural numbers {N} is infinite, the set of real numbers {R} is a larger infinite set. Hence in set notation, we have three different infinities: {N} < {R} < {C}. Since the natural numbers a very much smaller than the Real and Complex numbers, spacetime has plenty of room to remember all its spacetime processes, without the need for memory erasure.
11. Conclusions
In an analogous way to how Maxwell challenged the Second Law of Thermodynamics, and Szilard restored it through considerations of memory and choice, we have argued that “Spacetime Thinks”. Since the God of Spinoza and Einstein is equivalent to the universe, we have shown God exists, but with the added property of awareness. This is really not as surprising as it might seem at first, given that science is at the frontier of creating artificial intelligence out of the very components that were created during the Big Bang―when spacetime and all physical reality (including human consciousness) arise out of the chaos. And so, just as birds could fly before humans had built winged machines, in an analogous way, why not memory and consciousness arising from other natural spacetime processes―such as inside galactic centers, where memory and conscious choice manifest from extreme spacetimes. Moreover, since spacetime is contiguous (even if at the microscopic level it is connectedly-discrete), then galaxy by self-aware galaxy, this implies the universe itself, is self-aware―at least in a rudimentary graviton sign-switching way.
In closing, it seems self-evident that the universe is exceedingly more beautiful, creative and complex than any thought experiment could ever be―just as art and music are far more beautiful and intricate than disparate colored pigments and musical notes. Nevertheless, to make music and art, we begin with its constituent parts, as we have done so with spacetime memory and consciousness.
Acknowledgements
I wish to express my appreciation to James Earl Carter Jr., for living the simple principle of caring for humanity. Such a tenet is worshiped by many, but practiced by few. With the greatest of appreciation I wish to acknowledge Charles Darwin for his work while traveling aboard the Cherokee class HMS Beagle, resulting in the fundamental discovery of Natural Selection. With reverence to Isaac Newton for culminating the scientific revolution in his work Philosophiæ Naturalis Principia Mathematica, and to Albert Einstein for his thoughtfulness and ability to change the perception of world beneath our feet, as well as the universe above our heads―or is it the other way around? I also wish to thank to Steven Weinberg for carrying the torch of science, for his eloquent discussions on science and scientific history―and mostly for speaking in the tongue of genuineness. Thanks for taking the time to reply to my correspondence―doing so places Weinberg on the same good-hearted level as Einstein. To Jimena Canales―congratulations on your new book on “Physicist and the Philosophers,” and thank you very much for your encouragement: “May you have many more eggs hatching into many others”.