Received 17 December 2015; accepted 26 January 2016; published 29 January 2016

1. Introduction
Summetor was firstly introduced in research article, “Jeevan-Kushalaiah Method to Find the Coefficients of Characteristic Equation of a Matrix and Introduction of Summetor” by the authors Neelam Jeevan Kumar and Neelam Kushalaiah [1] . The Summetor operator name is taken from “sum” operator. Summetor operation is “Sum of all positive integers form one to n”. N-summet-k: Sum of all positive integers summeted k-times progressively.
N-summet-k is (Figure 1).
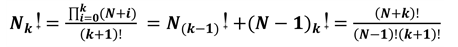 (i)
(i)
![]()
Figure 1. Representation of N-summet-k. Symbol and explanation: N is the real number or complex number. It must symbolize in Uppercase english letter only. k is the real number. It must symbolize in lowercase english letter only.  is Summetor operator symbol. Tale end “+” represents “summation”.
is Summetor operator symbol. Tale end “+” represents “summation”.
Example:
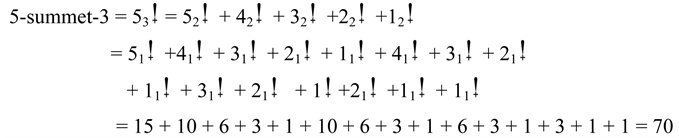
Properties:
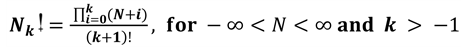 (i.a)
(i.a)
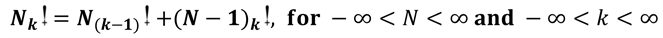 (i.b)
(i.b)
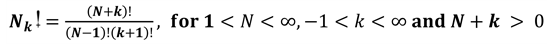 (i.c)
(i.c)
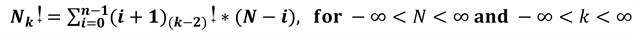 (i.d)
(i.d)
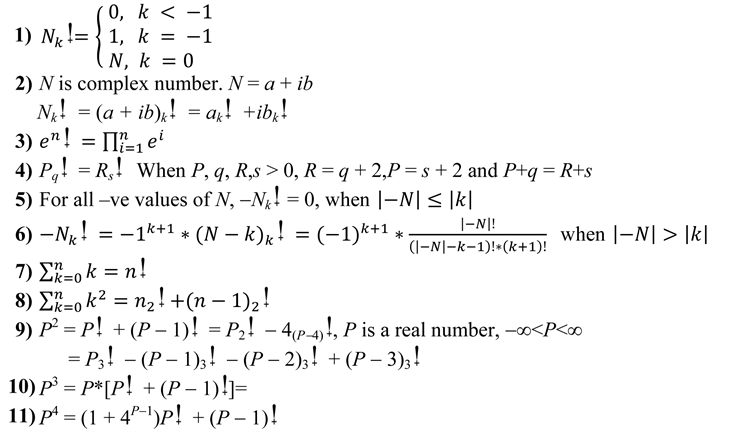
2. Tabulation and Graph
2.1. Tabulation
In the given Table 1, N is taken on vertically and k is taken on horizontally. The result of N-summet k is given with variable N from −9 to 15 and variable k from −3 to 10. N is positive value. The tabulation is the heart of N- summet-k.
In Table 2, elbow arrow between 6.4 and 10 proves 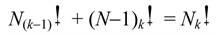
![]()
Table 1. N-summet-k values, where N = −9 to 0 and k = −3 to 9.
N (vertical bold numbers) and k (horizontal bold numbers).
![]()
Table 2. N-summet-k values, where N = 1 to 15 and k = −3 to 9.
But most commonly used formula to calculate N-summet-k is
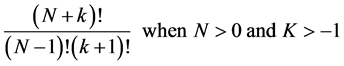
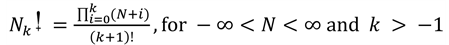
and
![]()
The dotted inclined lines shows Pascal triangle
2.2. Graph
Note: Taking ![]() = 0, for -1 > k,
= 0, for -1 > k, ![]()
where R > 0 and x is any integer or number or equation (Figures 2-4).
Proof-1: N < 0, N is any non fractional real number. Assume N = −1.From Equation (i.c) we get
![]()
Observe the tabulation; the N-summet-k value is 0.
Proof-2: k < -1, let k = −2.
From Equations (i.a) and (i.c) gives ![]()
Observe the tabulation, the N-summet-k value is 0.
3. Applications
3.1. Pascal’s Triangle (Figure 5)
Pascal’s triangle [2] is a triangular array of the binomial coefficients [3] [4] . Binomial coefficients are indexed
![]()
Figure 2. The range of N: −1 < N < 16 on X-axis and Nk![]() on Y-axis with variable k, 0 < k < 10.
on Y-axis with variable k, 0 < k < 10.
![]()
Figure 3. The range of N: −10 < N < 1 on X-axis and Nk![]() on Y-axis with variable k, 0 < k < 7.
on Y-axis with variable k, 0 < k < 7.
![]()
Figure 5. Pascal’s triangle. Last row coefficients are 1, 5, 10, 10, 5, 1 with n = 5. By using Summetor, the values of binomial coefficients with n = 5 are =6−1![]() , 50
, 50![]() , 41
, 41![]() , 32
, 32![]() , 23
, 23![]() , 14
, 14![]() . From the properties and tabulation, we can observe that the values of corresponding N-summet-k are = 1, 5, 10, 10, 5, 1.
. From the properties and tabulation, we can observe that the values of corresponding N-summet-k are = 1, 5, 10, 10, 5, 1.
by two non negative integers n and k written as![]() . It is the Coefficient of
. It is the Coefficient of ![]() term in polynomial expression of
term in polynomial expression of![]() . Where n rises from 0 to n.
. Where n rises from 0 to n.
The coefficients are given by the expression![]() . k varies from 0 to n.
. k varies from 0 to n.
By using Summetor or N-summet-k ![]() can be written as
can be written as
![]() (ii)
(ii)
where k varies from 0 to n in R.H.S and r varies from −1 to n−1 in L.H.S
A set, S has n-elements. The number of k combinations can be calculated by using Equation (ii)
Equation (ii) also gives combinations i.e., nCk, k varies from 0 to n formulated with N-summet-k.
Advantage of N-Summet-k
The computational time taken to calculate ![]() when
when![]() , k > 0 is much higher than that of (n − k)k
, k > 0 is much higher than that of (n − k)k![]()
The computation taken to calculate ![]() is t1, 1 < k < n and
is t1, 1 < k < n and
The computation taken to calculate ![]()
3.2. Pascal’s Matrix
The Pascal matrix [5] - [8] is an n × n dimension infinite matrix containing the binomial coefficients as its elements. The Pascal matrix generation is the matrix exponential of a special subdiagonal or superdiagonal matrix. The Three Pascal Matrices are Upper Triangular Matrix (Un), Lower Triangular Matrix (Ln) and Symmetric Matrix (Sn). Symmetric Matrix is product of Lower Triangular Matrix and Upper Triangular Matrix. The m is the values of Subdiagonal or superdiagonal elements and lies between −∞ and +∞.
9 × 9 Pascal Matrices (Un, Ln and Sn) represented rows as i = n = 9 and column as j = n = 9.
For positive values of diagonal elements, the Pascal matrices are
3.2.1. Upper Triangular Matrix, (Un)
Upper triangular matrix is formatted with exponential matrix containing superdiagonal elements.
![]()
![]()
Elements of upper triangular matrix are
![]() (iiia)
(iiia)
![]()
![]() (iiib)
(iiib)
3.2.2. Lower Triangular Matrix, (Ln)
Lower triangular matrix is formatted with exponential matrix containing subdiagonal elements.
![]()
![]()
Elements of lower triangular matrix are
![]() (iva)
(iva)
![]()
![]() (ivb)
(ivb)
Lower triangular matrix is transpose of upper triangular matrix vice versa.
![]()
3.2.3. Symmetric Matrix, (Sn)
![]() (va)
(va)
Elements of Sn for positive values of subdiagonal or superdiagonal elements.
![]() (vb)
(vb)
![]()
For positive values subdiagonal or superdiagonal elements
![]() (vc)
(vc)
The (Square box) in tabulation shows 12 × 12 Pascal Symmetric Matrix for positive values and;
The in tabulation shows mirror image elements positions of 5 × 5 Pascal upper triangular matrix.
Acknowledgements
N-summet-k has numerous applications in mathematics and physics like simplification of laguerre polynomials [9] [10] applied in quantum mechanics, in the radial part of the solution of the Schrödinger equation for a one- electron atom and Calculation of electrical voltage distribution across high voltage suspension type string insulator [11] and grading of string insulators [12] to improve string efficiency of high voltage overhead transmission line and so on. Author found the application of N-summet-k in above three applications but the subject regarding these applications not published yet. In future, the above three applications will be published by using N-summet-k.