Received 14 September 2015; accepted 15 December 2015; published 18 December 2015


1. Introduction
Continuous wavelet transform (CWT) [1] -[6] has been well known and widely applied for many years. In convention, CWT is defined with the timescale being positive. However, in practice, both positive and negative timescales are important for the CWT. For example, in earth’s polar motion [7] [8] , there are both prograde and retrograde annual wobbles. If one wants to use the CWT to analyze the annual wobbles, he should use a CWT defined with the timescale being real rather than positive.
CWT inversion has found few applications. The reason lies in that wavelet’s dual is assumed to be a reconstruction wavelet in conventional CWT inversion [6] . In fact, it is difficult for a CWT inversion using a reconstruction wavelet to obtain the admissibility constant. What will happen if wavelet’s dual is not a reconstruction wavelet or a localized function? This study tries to answer this question.
There has been a general inversion for linear time-frequency transform [9] . This inversion implies the inversion of CWT and the definition of wavelet’s dual. It is expressed as following theorem.
Deconvolution Theorem. For a time signal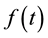 , its time-frequency transform
, its time-frequency transform
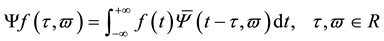 (1)
(1)
can be inverted by
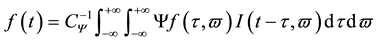 (2)
(2)
if
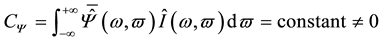 (3)
(3)
where 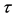 denotes time and
denotes time and 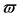 denotes frequency, overline “-” means conjugate operator, hat “^” means Fourier transform operator, for instances, the Fourier transform of kernel
denotes frequency, overline “-” means conjugate operator, hat “^” means Fourier transform operator, for instances, the Fourier transform of kernel 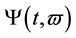 is
is
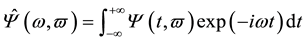 (4)
(4)
and Fourier transform of kernel’s dual 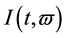 is
is
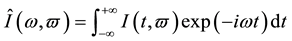 (5)
(5)
and constant 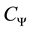 is called admissibility constant.
is called admissibility constant.
The name of this theorem comes from the fact that it gives the general way to inverting frequency-indexed convolutions. It is noted that the linear time-frequency transform (1) is a set of frequency-indexed convolutions. According to the deconvolution theorem, we will give a general inversion of CWT with timescale being real. This inversion gives an explicit definition of wavelet’s dual. The inversion implies a law: either wavelet or wavelet’s dual must integrate to zero. Also according to the inversion, we find that wavelet’s dual can be a harmonic besides a wavelet. Thus new CWT inversion formulas are obtained. The new formulas suggest the concept of normal wavelet transform, which is useful in time-frequency analysis and time-frequency filtering.
2. Inversion of CWT and Dual of Wavelet
For a time signal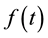 , its CWT is defined as
, its CWT is defined as
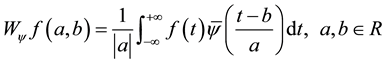 (6)
(6)
where 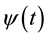 is a wavelet, a denotes timescale, b denotes time and “||” means absolute operator. It is important to note that the timescale a can be negative. For example, the timescale of a retrograde (i.e. clock-wise) harmonic movement on a complex plane is negative. Also note that the CWT is written in L1-norm rather than L2-norm. It has been proved that only L1-norm CWT spectrum is unbiased in detecting frequency [9] .
is a wavelet, a denotes timescale, b denotes time and “||” means absolute operator. It is important to note that the timescale a can be negative. For example, the timescale of a retrograde (i.e. clock-wise) harmonic movement on a complex plane is negative. Also note that the CWT is written in L1-norm rather than L2-norm. It has been proved that only L1-norm CWT spectrum is unbiased in detecting frequency [9] .
CWT (6) is composed of timescale-indexed convolutions. It can be regarded as a special time-frequency transform. Then, there is a CWT inversion corollary.
Inversion Corollary. For a time signal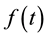 , its CWT (6) can be inverted by
, its CWT (6) can be inverted by
![]() (7)
(7)
if
![]() (8)
(8)
satisfies
![]() (9)
(9)
Proof. CWT (6) is a special time-frequency transform (1) with
![]() and
and![]() (10)
(10)
and
![]() (11)
(11)
Letting
![]() (12)
(12)
Then
![]() (13)
(13)
According to the deconvolution theorem, this inversion corollary is proved.
This inversion corollary gives a general way to inverting CWT. Relation (8) and (9) establish an explicit definition for wavelet’s dual. This means that a function ![]() simply satisfying relation (8) and (9) is called a dual of wavelet
simply satisfying relation (8) and (9) is called a dual of wavelet![]() . Consider that the integration in (8), if existing, is naturally a constant. Such definition is very explicit, because relations (8) and (9) explicate how to obtain a dual of wavelet. Furthermore, in inversion (7), the timescale a spans over entire real field rather than half real field.
. Consider that the integration in (8), if existing, is naturally a constant. Such definition is very explicit, because relations (8) and (9) explicate how to obtain a dual of wavelet. Furthermore, in inversion (7), the timescale a spans over entire real field rather than half real field.
3. A CWT Inversion Law
Observing the relation (8), one can find that it is necessary for the wavelet and its dual of CWT (6) to satisfy
![]() (14)
(14)
To make (14) true, there must be that either
![]() (15)
(15)
or
![]() (16)
(16)
Thus, there is a CWT inversion law.
Inversion Law. In CWT inversion, either wavelet or its dual must integrate to zero.
This law applies to any CWT inversion and can never be violated. Such law breaks the traditional zero-integration requirement on wavelet. The zero-integration requirement on wavelet is made in the case that the dual of the wavelet is exactly the wavelet itself. Such case is very special. As shown by the inversion corollary, a CWT with its wavelet being unevenly undulant is still possible to be inverted.
4. CWT Inversion with Wavelet’s Dual Being a Harmonic
Making a CWT inversion is equivalent to finding a dual of wavelet. In tradition, wavelet’s dual is assumed to be a reconstruction wavelet or a localized function [6] . It is interesting to find that wavelet’s dual can be a harmonic which is not local. Letting
![]() (17)
(17)
where ![]() is a nonzero real, the admissibility constant becomes
is a nonzero real, the admissibility constant becomes
![]() (18)
(18)
This means, for a time signal![]() , its CWT (6) can be inverted by
, its CWT (6) can be inverted by
![]() (19)
(19)
Particularly, if![]() , inversion (19) is simply
, inversion (19) is simply
![]() (20)
(20)
Inversion (20) has been found by Liu and Hsu 2012. It plays a main role in the concept of normal wavelet transform [9] . Here, for the first time, inversion (19) is found. It means that a CWT can be inverted by dilating and translating a harmonic! The important reason lies in inversion (19) is that a harmonic is evenly undulant no matter the wavelet is evenly undulant or not. Inversion (19) shows that the dual of a wavelet is not unique. For a wavelet, the number of its duals is innumerous. For a CWT, its inversion can be of innumerous forms.
In inversion (19), there is requirement for the wavelet is that
![]() (21)
(21)
This requirement can be easily to meet by letting
![]() (22)
(22)
where ![]() is a window. Also note that wavelet (22) is usually inadmissible.
is a window. Also note that wavelet (22) is usually inadmissible.
5. Normal Wavelet Transform
For time signal![]() , its CWT (6) is called a normal wavelet transform if the wavelet is defined as
, its CWT (6) is called a normal wavelet transform if the wavelet is defined as
![]() (23)
(23)
where window ![]() satisfies
satisfies
1) ![]() (24)
(24)
and
2) ![]() (25)
(25)
where “ ![]() “ means “if and only if”. As a special CWT, the normal wavelet transform is useful in time-fre- quency analysis and time-frequency-filtering.
“ means “if and only if”. As a special CWT, the normal wavelet transform is useful in time-fre- quency analysis and time-frequency-filtering.
5.1. Time-Frequency Analysis
If applying a normal wavelet transform to a harmonic
![]() (26)
(26)
It is easy to observe that
1) ![]() (27)
(27)
2) ![]() (28)
(28)
Relations (27) and (28) assure that the normal wavelet transform is accurate and useful in time-frequency analysis. At first, Relation (27) means that the normal wavelet transform can exactly (i.e. without bias) detect the immediate (i.e. local) frequency of a harmonic. Secondly, relation (28) means that the normal wavelet transform can exactly detect the immediate amplitude and phase of a harmonic. It is important to note that, relation (27) does not hold if the CWT (6) is not defined in L1-norm. Different from the S-transform [10] as well as General S-transform [11] , the normal wavelet transform can detect the immediate rather than initial phase of a harmonic. Similar to S-transform as well as General S-transform, the normal wavelet transform can do time frequency filtering.
5.2. Time-Frequency Filtering
According to (20), the normal wavelet transform can be inverted simply by
![]() (29)
(29)
because
![]() (30)
(30)
This inversion suggests that
![]() (31)
(31)
where S is some time-frequency area and ![]() denotes the filtered signal. (31) is the basic formula for time-frequency filtering by using the normal wavelet transform.
denotes the filtered signal. (31) is the basic formula for time-frequency filtering by using the normal wavelet transform.
We here provide a numeric example of time-frequency analysis and time-frequency filtering by using the normal wavelet transform. A test time signal ![]() is constructed (Figure 1). It is composed of three intermittent harmonic sub-signals and some noises. We apply a normal wavelet transform to this signal by letting
is constructed (Figure 1). It is composed of three intermittent harmonic sub-signals and some noises. We apply a normal wavelet transform to this signal by letting
![]() (32)
(32)
The normal wavelet transform spectrum is obtained (Figure 2). One can observe that there are clearly three significant sub-signal in the original signal. According to the spectrum significance, three time-frequency areas can be determined. Then, according to (31), one can recover the three sub-signals in time domain (Figure 3). The recovered sub-signals are well fitted to its original counterparts, which shows the good time-frequency filtering function of the normal wavelet transform.
6. Conclusion
According to deconvolution theorem, this study explicates the way to inverting continuous wavelet transform (CWT) and the definition of wavelet’s dual. We prove that, in CWT inversion, either wavelet or its dual must integrate to zero. This study shows that wavelet’s dual can be a harmonic, which leads to new CWT inversion for-
![]()
Figure 2. Normal wavelet spectrum of the test time signal ![]() with
with ![]() (the white closed lines denote three significant time-frequency areas).
(the white closed lines denote three significant time-frequency areas).
![]()
Figure 3. Three sub-signals (blue) and their corresponding recovered sub-signals (red) (a, b, and c).
mulas. One of the formulas justifies the concept of normal wavelet transform, which is useful in time-frequency analysis and time-frequency filtering.
Acknowledgements
We thank the Editor and the referee for their comments. This study is supported by NSFC 41074050 and by 2011YQ120045 of Ministry of Science and Technology of the People’s Republic of China.