On Separation between Metric Observers in Segal’s Compact Cosmos ()
1. Motivation and Introduction
The first author has been interested in GR (“GR” is for General Relativity) research for quite a while and he concentrated on a few most symmetric spacetimes ( [1] , [2] , and more). Later (see [3] , [4] ) he has become a strong believer in Segal’s Chronometric Theory (see [5] , electronic archive arranged by Levichev), and he is attempting to modify Segal’s Theory (see [6] , a key publication). The collaboration of the two current authors is based on their mutual interest in Penrose-Hameroff approach to consciousness (see its update in [7] , [8] ). Specifically, we are putting forward an alternative definition of separation between space-times. In [9] , the original definition was based on bringing up a Newtonian limit in GR. Our definition has been introduced in [10] , [11] , and we now present it in much more detail.
Recall the Lie group 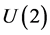 as the totality of all two-by-two matrices z (with complex entries allowed) satisfying
as the totality of all two-by-two matrices z (with complex entries allowed) satisfying
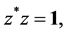 (1.1)
(1.1)
where 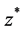 is the transpose and complex conjugate of z, and
is the transpose and complex conjugate of z, and 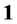 is the unit matrix. Now, define the Lie group
is the unit matrix. Now, define the Lie group 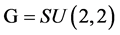 as consisting of all four-by-four matrices g (with complex entries allowed) satisfying
as consisting of all four-by-four matrices g (with complex entries allowed) satisfying
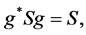 (1.2)
(1.2)
where S is the diagonal matrix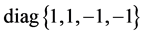 . Recall the well-known linear-fractional G-action on
. Recall the well-known linear-fractional G-action on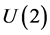 :
:
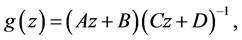 (1.3)
(1.3)
where a matrix g from G is determined by its ![]() blocks A, B, C, D.
blocks A, B, C, D.
In Table I of [12] , the matrices ![]() are chosen as basic vectors of the (fifteen-dimensional) Lie algebra
are chosen as basic vectors of the (fifteen-dimensional) Lie algebra![]() , whereas
, whereas ![]() are the corresponding vector fields on
are the corresponding vector fields on![]() . The vector fields
. The vector fields ![]() are determined by the G-action (1.3). As explained in [12] , subscripts i, j take on −1, 0, 1, 2, 3, 4, and the convention
are determined by the G-action (1.3). As explained in [12] , subscripts i, j take on −1, 0, 1, 2, 3, 4, and the convention ![]() (resulting in
(resulting in![]() ) holds.
) holds.
The Lorentzian inner product on ![]() is introduced in such a way that left-invariant vector fields
is introduced in such a way that left-invariant vector fields ![]() form an orthonormal basis (following [12] , we use +, −, −, − signature). The resulting product on
form an orthonormal basis (following [12] , we use +, −, −, − signature). The resulting product on ![]() is bi-invariant (see [6] ), and
is bi-invariant (see [6] ), and ![]() below denotes the Lorentzian inner product of tangent vectors
below denotes the Lorentzian inner product of tangent vectors ![]() at a point z of
at a point z of![]() . The spacetime thus obtained is denoted by
. The spacetime thus obtained is denoted by ![]() (the meaning of the subscript will become clear in the next section). Transformations (1.3) are conformal in
(the meaning of the subscript will become clear in the next section). Transformations (1.3) are conformal in ![]() (a word of caution: this spacetime has been denoted as D in [6] ). As it follows from Table I of [12] , the vector fields
(a word of caution: this spacetime has been denoted as D in [6] ). As it follows from Table I of [12] , the vector fields![]() , generate isometries in
, generate isometries in![]() . The corresponding subgroup K in G consists of all matrices (1.2) with
. The corresponding subgroup K in G consists of all matrices (1.2) with![]() .
.
For what follows, it is instrumental to introduce a certain bi-invariant Riemannian inner product on![]() . To do so, we recall that vector fields
. To do so, we recall that vector fields ![]() constitute a basis of the Lie algebra
constitute a basis of the Lie algebra![]() . This algebra is a direct sum of its center with
. This algebra is a direct sum of its center with![]() . Namely,
. Namely, ![]() generates the center, whereas
generates the center, whereas![]() ,
, ![]() ,
, ![]() are basic vectors in
are basic vectors in![]() . The Riemannian metric is determined by the demand on left-invariant vector fields
. The Riemannian metric is determined by the demand on left-invariant vector fields![]() ,
, ![]() ,
, ![]() ,
, ![]() to form an orthonormal basis. The corresponding Riemannian space is denoted
to form an orthonormal basis. The corresponding Riemannian space is denoted![]() . Again,
. Again, ![]() is
is![]() , as a manifold. Our
, as a manifold. Our ![]() below denotes the Riemannian inner product of tangent vectors
below denotes the Riemannian inner product of tangent vectors ![]() at a point z of
at a point z of![]() . In the forthcoming sections the corresponding volume form on
. In the forthcoming sections the corresponding volume form on ![]() will be instrumental. From Table I of [12] , it follows that the group K acts as a group of both Lorentzian and Riemannian isometries.
will be instrumental. From Table I of [12] , it follows that the group K acts as a group of both Lorentzian and Riemannian isometries.
Notice that, as a group, ![]() is not a direct product of its center with the subgroup
is not a direct product of its center with the subgroup![]() . The double cover
. The double cover ![]() of
of ![]() is the direct product
is the direct product ![]() (with
(with ![]() represented by
represented by![]() ). The covering map sends
). The covering map sends ![]() into the matrix
into the matrix ![]() in
in![]() . The corresponding Lorentzian metric on
. The corresponding Lorentzian metric on ![]() is of the form
is of the form
![]() (1.4)
(1.4)
Here the variable t is along ![]() whereas
whereas ![]() is for the standard Riemannian metric on
is for the standard Riemannian metric on![]() . More details are given in our Appendix A, where u denotes a matrix from
. More details are given in our Appendix A, where u denotes a matrix from![]() . Our Appendix B is dedicated to a certain one-parameter group of transformations (1.3).
. Our Appendix B is dedicated to a certain one-parameter group of transformations (1.3).
It is well-known ( [12] , [13] ) that the (above introduced) covering map is a Lorentzian isometry. Infinitesimal G-action on ![]() is presented in Table I of [12] . It is known (see [13] ) that action (1.3) can be lifted to a global conformal G-action on
is presented in Table I of [12] . It is known (see [13] ) that action (1.3) can be lifted to a global conformal G-action on![]() . Using the corresponding commutative diagram, one can show that the lifted action of the group K is as follows:
. Using the corresponding commutative diagram, one can show that the lifted action of the group K is as follows:
![]() (1.5)
(1.5)
Also, it is easily verifiable that for the Riemannian metric
![]() (1.6)
(1.6)
on ![]() the (above specified) covering map is a Riemannian isometry from
the (above specified) covering map is a Riemannian isometry from ![]() onto
onto![]() .
.
It makes sense to mention how a suitable version of the Einstein static universe, ![]() , can be introduced in the context of our work (the subscript uc is for universal cover). To be more precise,
, can be introduced in the context of our work (the subscript uc is for universal cover). To be more precise, ![]() should be called universal cosmos ( [14] ) or Segal’s universal cosmos ( [13] ). The universal cover
should be called universal cosmos ( [14] ) or Segal’s universal cosmos ( [13] ). The universal cover ![]() of
of ![]() is
is![]() , topologically. The G-action on
, topologically. The G-action on ![]() is canonically lifted to the Guc-action on
is canonically lifted to the Guc-action on ![]() (the latter action preserves the causal structure of
(the latter action preserves the causal structure of![]() ). In a cosmological model based on
). In a cosmological model based on![]() , there is a conformal invariant R, interpreted as the radius of a three-dimensional (physical) space
, there is a conformal invariant R, interpreted as the radius of a three-dimensional (physical) space![]() . I. Segal (in [14] and in other publications) has put this R for the (long wanted by Dirac and others) third fundamental constant additionally to the speed of light and to the Planck’s constant. It is known that to model particles on
. I. Segal (in [14] and in other publications) has put this R for the (long wanted by Dirac and others) third fundamental constant additionally to the speed of light and to the Planck’s constant. It is known that to model particles on![]() , one can start with the world
, one can start with the world![]() , a compact one. The respective property is called automatic periodicity ( [15] , p. 202), and it allows us to only deal with compact spacetimes
, a compact one. The respective property is called automatic periodicity ( [15] , p. 202), and it allows us to only deal with compact spacetimes ![]() and
and ![]() (which explains our compact Segal’s cosmos terminology).
(which explains our compact Segal’s cosmos terminology).
More precisely, we deal with two classes of spacetimes: ![]() and
and![]() . Roughly speaking, the first class is obtained by application of all transformations (3) to
. Roughly speaking, the first class is obtained by application of all transformations (3) to![]() ; details follow in the next section (where
; details follow in the next section (where ![]() will also be defined).
will also be defined).
2. On the Notion of Separation between Spacetimes: The Main Definition and Related Properties
The separation (or distance) ![]() will be defined for any pair x, y of spacetimes from
will be defined for any pair x, y of spacetimes from ![]() (or from
(or from![]() ).
).
As mentioned, the totality of all isometries in ![]() is the group K of all matrices (1.2) with
is the group K of all matrices (1.2) with![]() . Each member E of the class
. Each member E of the class ![]() will be now put in correspondence with an element x of the homogeneous space
will be now put in correspondence with an element x of the homogeneous space
G/K. Namely, each element (or coset) x of G/K is specified by an element g from G:![]() . One and the same x can be determined by another element (say,
. One and the same x can be determined by another element (say,![]() ) from G: gK = g1K. For such a pair
) from G: gK = g1K. For such a pair![]() ,
,
there exists such k from K, that![]() . When the subgroup K is viewed as an element of G/K, denote K as
. When the subgroup K is viewed as an element of G/K, denote K as![]() . This
. This ![]() we put into correspondence with
we put into correspondence with ![]() (which has been described in Section 1). As a manifold, each element x of
(which has been described in Section 1). As a manifold, each element x of ![]() is
is![]() . In what follows, we use
. In what follows, we use ![]() (rather than
(rather than![]() ) to denote the (Lorentzian) inner product of vectors
) to denote the (Lorentzian) inner product of vectors ![]() from the tangent space T(E0) at z. This inner product has been introduced in our Section 1. To define spacetime E corresponding to a coset x = gK, it is enough to specify the inner product
from the tangent space T(E0) at z. This inner product has been introduced in our Section 1. To define spacetime E corresponding to a coset x = gK, it is enough to specify the inner product
![]() , see (2.2) below. Such a transformation g is conformal in E0. Namely, given vectors
, see (2.2) below. Such a transformation g is conformal in E0. Namely, given vectors ![]() from the tangent space T(E0) at z, the inner product
from the tangent space T(E0) at z, the inner product ![]() at
at ![]() of their images (under the tangent map
of their images (under the tangent map![]() ) satisfies
) satisfies
![]() (2.1)
(2.1)
The everywhere positive function ![]() is known as the square of conformal coefficient. Frequently, we will simply refer to this
is known as the square of conformal coefficient. Frequently, we will simply refer to this ![]() as to a conformal coefficient. Given vectors
as to a conformal coefficient. Given vectors ![]() from the tangent space
from the tangent space ![]() at z, their inner product can be defined as follows:
at z, their inner product can be defined as follows:
![]() (2.2)
(2.2)
where ![]() is calculated at z. Notice, that h here is the (above mentioned) function on
is calculated at z. Notice, that h here is the (above mentioned) function on ![]() determined by g It is easy to show that (2.2) is equivalent to the condition for g to be an isometry between
determined by g It is easy to show that (2.2) is equivalent to the condition for g to be an isometry between ![]() and
and![]() :
:
![]() (2.3L)
(2.3L)
Here the right hand side of (2.3L) is calculated in ![]() at z, and it defines the inner product
at z, and it defines the inner product ![]() of vectors
of vectors ![]() and
and ![]() at
at![]() . To avoid verification of (2.2)-(2.3L) equivalence, we define the Lorentzian metric in E in terms of (2.3L). Similarly, we define the following Riemannian metric in E:
. To avoid verification of (2.2)-(2.3L) equivalence, we define the Lorentzian metric in E in terms of (2.3L). Similarly, we define the following Riemannian metric in E:
![]() (2.3R)
(2.3R)
where the positive definite inner product in the right hand side of (2.3R) has been introduced in our Section 1.
Let us show that, given a coset x in G/K, (2.3L) correctly defines a Lorentzian metric on![]() , whereas (2.3R) correctly defines a Riemannian metric on
, whereas (2.3R) correctly defines a Riemannian metric on![]() :
:
Scholium 2.1. The inner product (2.3L) (respectively, the inner product (2.3R)) is independent of the choice of g which represents a coset x.
Proof. If x is represented as g1K, then ![]() where k is a certain element of the group K. Given such a representation, the analogue of (2.3R) is
where k is a certain element of the group K. Given such a representation, the analogue of (2.3R) is
![]() (2.4)
(2.4)
where the right hand side of (2.4) is calculated in ![]() at z, and it defines the inner product
at z, and it defines the inner product ![]() of vectors
of vectors ![]() and
and ![]() at
at![]() . We have to show that (2.4) introduces the same metric structure on
. We have to show that (2.4) introduces the same metric structure on ![]() as (2.3L) does. To do so, we rewrite (2.3L) in the form of
as (2.3L) does. To do so, we rewrite (2.3L) in the form of
![]() (2.5)
(2.5)
where the right hand side is calculated at![]() , and the left hand side is calculated at
, and the left hand side is calculated at![]() .
.
However, ![]() in (2.5) equals
in (2.5) equals ![]() in (2.4) since k is a Lorentzian isometry in
in (2.4) since k is a Lorentzian isometry in![]() . Comparison of (2.4) with (2.5) finishes the proof. The verification process, that (2.3R) is independent of representative, copies the one for (2.3L). □
. Comparison of (2.4) with (2.5) finishes the proof. The verification process, that (2.3R) is independent of representative, copies the one for (2.3L). □
Let us notice (see [16] ) that each ![]() can be interpreted as a spacetime corresponding to a certain (global) observer. A word of caution: [16] treats the universal cover of
can be interpreted as a spacetime corresponding to a certain (global) observer. A word of caution: [16] treats the universal cover of ![]() whereas we only deal with compact spacetimes here.
whereas we only deal with compact spacetimes here.
Remark 2.2. We have thus defined the class ![]() of spacetimes. Our class
of spacetimes. Our class ![]() can be similarly introduced in terms of the Lorentzian manifold
can be similarly introduced in terms of the Lorentzian manifold ![]() (the 2-cover of
(the 2-cover of![]() ) with the (lifted) G-action on
) with the (lifted) G-action on![]() .
.
Given a (1.3)-transformation g of (Lorentzian)![]() , define the following subsets of
, define the following subsets of![]() :
:
![]() (2.6)
(2.6)
![]() (2.7)
(2.7)
here ![]() is the square of the conformal coefficient at z of the transformation g. A (non-negative) number
is the square of the conformal coefficient at z of the transformation g. A (non-negative) number ![]() is defined as follows:
is defined as follows:
![]() (2.8)
(2.8)
where ![]() is for the volume of a set S in
is for the volume of a set S in ![]() (with the volume form introduced in our Section 1). Clearly, expressions inside the logarithms in (2.8) can be interpreted as corresponding cumulative distortions of the original metric structure in
(with the volume form introduced in our Section 1). Clearly, expressions inside the logarithms in (2.8) can be interpreted as corresponding cumulative distortions of the original metric structure in![]() . To be sure of convergence of all of the integrals involved, it is enough to mention that each of the two integrands is a continuous function over the corresponding region of integration, whereas each of the regions (2.6), (2.7) is a compact set.
. To be sure of convergence of all of the integrals involved, it is enough to mention that each of the two integrands is a continuous function over the corresponding region of integration, whereas each of the regions (2.6), (2.7) is a compact set.
To further deal with (2.8), we now proceed with more technicalities. Clearly, ![]() can be viewed as
can be viewed as ![]() with
with![]() ,
,![]() . The integration in a is over
. The integration in a is over![]() , whereas in c the integration is over
, whereas in c the integration is over![]() .
.
Examples of integrals ![]() evaluations are given in our Appendix C (see Theorem C.5). Notice that
evaluations are given in our Appendix C (see Theorem C.5). Notice that
![]() (2.9)
(2.9)
which follows from (2.8) because in this case![]() , a constant function on
, a constant function on![]() . As a result of
. As a result of![]() , each of the two terms in the sum (2.8) is zero.
, each of the two terms in the sum (2.8) is zero.
Scholium 2.3. Given the (1.3)-transformation g and isometries![]() ,
, ![]() , the following holds:
, the following holds:
![]() (2.10)
(2.10)
where![]() .
.
Proof. To prove (2.10), we will now show that each of the four numbers (a, b, c, and d) remain the same when we switch from ![]() to
to![]() . Namely:
. Namely:
![]()
Similarly,![]() . Hence,
. Hence, ![]() , and
, and![]() , due to the K-invariance of the volume form.
, due to the K-invariance of the volume form.
Let us now use the variable ![]() in the integral a of
in the integral a of ![]() over
over![]() : the integrand is then
: the integrand is then
![]() , the region of integration is
, the region of integration is![]() , and there is no extra factor in the
, and there is no extra factor in the
integrand since ![]() is a transformation from the group K. Similarly, number c remains the same when we switch from
is a transformation from the group K. Similarly, number c remains the same when we switch from ![]() to
to![]() . □
. □
Now, if two cosets are represented as![]() ,
, ![]() , define the distance
, define the distance ![]() as
as
![]() (2.11)
(2.11)
where![]() . The number
. The number ![]() is independent of representatives since if x is represented by
is independent of representatives since if x is represented by![]() , and y is represented by
, and y is represented by![]() , then for
, then for![]() ,
, ![]() according to (2.10).
according to (2.10).
Corollary 2.4. In the above settings, ![]() where
where ![]() and
and![]() .
.
A word of caution: we use the term distance but we are not sure that the corresponding triangle inequality holds (even locally) for (2.11). However, we prove (below) that (2.11) is symmetric:![]() , and G-invariant:
, and G-invariant:
![]() (2.12)
(2.12)
for arbitrary f from G (where we have in mind the canonical action of G in G/K).
As regards G-invariance, one can think of a possible relation of our definition (2.11) to the canonical inner product in the symmetric space G/K. This we do not discuss here.
Scholium 2.5. The distance (2.11) is symmetric:![]() .
.
Proof. As justified by our Corollary 2.4, assume that ![]() and
and![]() . Define
. Define
![]()
where![]() , and where we use
, and where we use ![]() (rather than z, as before) to denote a matrix in
(rather than z, as before) to denote a matrix in![]() . Tilde (below) indicates that computations are performed in E rather than in
. Tilde (below) indicates that computations are performed in E rather than in![]() .
.
For ![]() the following is true:
the following is true:
![]() since, due to (2.3R), g is an isometry between the two Riemannian spaces. Similarly,
since, due to (2.3R), g is an isometry between the two Riemannian spaces. Similarly,![]() . The new integrand is then
. The new integrand is then![]() , the new region of integration is
, the new region of integration is![]() , and there is no extra factor in the integrand since g is an isometry between the two Riemannian spaces in question. We have thus proven that
, and there is no extra factor in the integrand since g is an isometry between the two Riemannian spaces in question. We have thus proven that![]() . Similarly,
. Similarly,![]() . We have thus proven the equality
. We have thus proven the equality![]() , which results in
, which results in![]() , the symmetry property of the distance between spacetimes. □
, the symmetry property of the distance between spacetimes. □
3. Concluding Remarks and Future Research Insights
Examples of integrals ![]() evaluations (in case of a certain one-parameter group of conformal transforma- tions) are given in our Appendix C. It is of interest to know whether Theorem C.5 holds for other transforma- tions from G =
evaluations (in case of a certain one-parameter group of conformal transforma- tions) are given in our Appendix C. It is of interest to know whether Theorem C.5 holds for other transforma- tions from G =![]() . Evaluations in Appendix C indicate that definition (2.11) of distance between spacetimes seems to be quite a working one. As part of future research, it will be of interest to apply our definition in the case where the original spacetime is F (here we refer to the DLF-theory, [6] ). In that case, the underlying manifold is (non-compact!)
. Evaluations in Appendix C indicate that definition (2.11) of distance between spacetimes seems to be quite a working one. As part of future research, it will be of interest to apply our definition in the case where the original spacetime is F (here we refer to the DLF-theory, [6] ). In that case, the underlying manifold is (non-compact!)![]() , rather than
, rather than![]() . Preliminary calculations indicate that a conformal coefficient might be unbounded. We will thus have to deal with improper 4D integrals, and the question of convergence will have to be studied first.
. Preliminary calculations indicate that a conformal coefficient might be unbounded. We will thus have to deal with improper 4D integrals, and the question of convergence will have to be studied first.
Appendix A: Parameterizations of U(2) and E(2)
The following presentation for E(2), the 2-cover of![]() , has been widely used in the literature. Consider the direct sum E6 = E2 Å E4 of two Euclidean spaces: E2 with rectangular coordinates
, has been widely used in the literature. Consider the direct sum E6 = E2 Å E4 of two Euclidean spaces: E2 with rectangular coordinates![]() ,
, ![]() , and E4 with rectangular coordinates
, and E4 with rectangular coordinates![]() . Each “event” in E(2) is a 6-tuple
. Each “event” in E(2) is a 6-tuple![]() , satisfying
, satisfying
![]() (A1)
(A1)
and
![]() (A2)
(A2)
Clearly, E(2) is S1 × S3, topologically. The earlier introduced ![]() (see Section 2) is
(see Section 2) is![]() , whereas the matrix u from
, whereas the matrix u from ![]() is specified as follows:
is specified as follows:
![]() (A3)
(A3)
The covering map from E(2) onto ![]() takes the pair
takes the pair ![]() into the matrix
into the matrix![]() , an element z of the group
, an element z of the group![]() :
:
![]() (A4)
(A4)
Given a matrix z in![]() , the factors
, the factors ![]() and u are defined up to a sign, only. In terms of E6, it is helpful to consider a pseudo-Euclidean metric
and u are defined up to a sign, only. In terms of E6, it is helpful to consider a pseudo-Euclidean metric
![]() (A5L)
(A5L)
and an Euclidean metric
![]() (A5R)
(A5R)
It is known (see [14] , p. 40) that the restriction of (A5L) onto E(2) = S1 ´ S3 coincides with metric (1.4) of our Section 1. Similarly, the restriction of (A5R) onto E(2) coincides with metric (1.5).
Appendix B: The Case of a Certain One-Parameter Group of Conformal Transformations
This group consists of all (1.3)-transformations g of the form:
![]() (B.1)
(B.1)
with
![]()
where![]() ,
, ![]() ,
, ![]() being a real parameter. This subgroup is contained in a (two-dimensional) subgroup A (from the Iwasawa decomposition
being a real parameter. This subgroup is contained in a (two-dimensional) subgroup A (from the Iwasawa decomposition ![]() = KAN). The
= KAN). The ![]() below is for the (positive) square root of the conformal factor
below is for the (positive) square root of the conformal factor![]() . The latter has been defined by our (2.1). To simplify notation, we, sometimes, use the same symbol (like z or
. The latter has been defined by our (2.1). To simplify notation, we, sometimes, use the same symbol (like z or![]() , below) to denote both an element of E(2) and a matrix in E0. The statement and the proof of the following theorem presume usage of rectangular coordinates in Euclidean E6: see Appendix A.
, below) to denote both an element of E(2) and a matrix in E0. The statement and the proof of the following theorem presume usage of rectangular coordinates in Euclidean E6: see Appendix A.
Theorem B.1. The image ![]() of z in E(2) and the conformal factor
of z in E(2) and the conformal factor ![]() at z (under the lift of the (B.1)― transformation g) are as follows:
at z (under the lift of the (B.1)― transformation g) are as follows:
![]() (B.2)
(B.2)
![]() (B.3)
(B.3)
Proof. Notice that due to (A3) and (A4) from Appendix A, the formulas (B.2) correctly define the transformation on the level of E0 (when z and ![]() are matrices). To prove this first part, we use (B.1) in a straightforward way and (omitting routine details of the calculation) determine (B.2). At this stage of the proof we cannot be sure that
are matrices). To prove this first part, we use (B.1) in a straightforward way and (omitting routine details of the calculation) determine (B.2). At this stage of the proof we cannot be sure that ![]() is the conformal coefficient. To prove that it is, apply the differential operator d to both sides of (B.2) in order to express
is the conformal coefficient. To prove that it is, apply the differential operator d to both sides of (B.2) in order to express
![]() (B.4)
(B.4)
in terms of differentials![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() . Comparison of the obtained expression with (A5L) verifies (B.3). □
. Comparison of the obtained expression with (A5L) verifies (B.3). □
Remark B.2. In the case considered, there is an alternative way to determine the conformal factor (B.3). It is as follows [17] , Theorem 3: for a (1.3)-transformation g, the following equality holds for the conformal factor at z:
![]() (B.5)
(B.5)
One can verify that (B.5), when applied in the (B.1)-case, results in (B.3).
It is of interest to determine all fixed points (that is, matrices ![]() with
with ![]() property) of the transformation (B.1).
property) of the transformation (B.1).
Scholium B.3. The totality of all fixed points of (B.1) is a pair of circles. One of the circles is given by equations![]() ,
,![]() . The other circle is given by equations
. The other circle is given by equations![]() ,
,![]() .
.
Proof. As it follows from (B.1), the totality of all fixed points is the solution set of
![]() (B.6)
(B.6)
equality of two matrices. Comparison of first entries in second rows results in
![]() (B.7)
(B.7)
Since g is not an identity transformation,![]() . If
. If![]() , then comparison of first entries in the first rows results in
, then comparison of first entries in the first rows results in![]() , that is,
, that is,![]() . Comparison of second entries in second rows results in
. Comparison of second entries in second rows results in![]() . Now, if
. Now, if ![]() in (B.7), then, again,
in (B.7), then, again,![]() . □
. □
Our next goal is to prove that each fixed point (of a given (B.1)―transfor-mation) is an extreme point of the conformal coefficient![]() : maximum is reached at each point of one circle whereas minimum is reached at each point of the other circle.
: maximum is reached at each point of one circle whereas minimum is reached at each point of the other circle.
Scholium B.4. If ![]() at
at![]() , then
, then ![]() is not a point of extremum for
is not a point of extremum for![]() .
.
Proof. If ![]() at
at![]() , then
, then![]() ,
, ![]() can be chosen as two (of the total of four) free real variables at the vicinity of
can be chosen as two (of the total of four) free real variables at the vicinity of![]() . If
. If ![]() is a point of extremum for
is a point of extremum for![]() , then each of the two partial derivatives of h (w.r.t.
, then each of the two partial derivatives of h (w.r.t.![]() , and w.r.t.
, and w.r.t.![]() ) vanish at
) vanish at![]() . However, that would have resulted in vanishing of
. However, that would have resulted in vanishing of ![]() at
at![]() . □
. □
Corollary B.5. If ![]() is an extreme point for h, then
is an extreme point for h, then ![]() (that is,
(that is,![]() ).
).
Corollary B.6. At the point of extremum for the conformal coefficient, either![]() , or
, or ![]() (that is,
(that is, ![]() , or
, or![]() ).
).
Proof follows from the expression ![]() which holds at every point z where
which holds at every point z where![]() . □
. □
Corollary B.7. An extreme value of ![]() is reached at
is reached at ![]() if and only if
if and only if ![]() is a fixed point of (B.1). One can verify that the two extreme values are
is a fixed point of (B.1). One can verify that the two extreme values are ![]() and
and ![]() where
where ![]() is the (non-zero) value of the parameter in (B.1).
is the (non-zero) value of the parameter in (B.1).
Appendix C: Evaluations of Integrals (2.8) for the Case of Appendix B Transformations in E(2)
We start with the form
![]() (C.1)
(C.1)
on the torus T = S1 ´ S3, see our Theorem B.1. Now, T+ is for the part of T where![]() , T− is for the part of T where
, T− is for the part of T where![]() . Introduce
. Introduce
![]() (C.2)
(C.2)
![]() (C.3)
(C.3)
where in both cases we have in mind the volume form which has been introduced on T in Section 2.
A word of caution: the function (C.1) is the inverse of the conformal coefficient (B.3). Nevertheless, the findings (which follow) of this Appendix C are relevant to the Appendix A content since k in (C.2), (C.3) can be any integer.
The majority of these Appendix C findings are due to V. V. Ivanov (Sobolev Institute of Mathematics, Novosibirsk, Russia).
Parameterize T as follows:
![]() (C.4)
(C.4)
In terms of these parameters, (C.1) becomes
![]() (C.5)
(C.5)
The integrals (C.2), (C.3) are reduced as follows:
![]() (C.6)
(C.6)
where
![]() (C.7)
(C.7)
Here we consider the rectangle![]() , and
, and![]() ,
,![]() . Notice that the integrals (C.6) and (C.7) are independent of the sign of
. Notice that the integrals (C.6) and (C.7) are independent of the sign of ![]() which allows us to stay with
which allows us to stay with![]() , only. The next step is to interpret
, only. The next step is to interpret![]() ,
, ![]() as polar coordinates on the x, y plane:
as polar coordinates on the x, y plane:
![]() (C.8)
(C.8)
Our function (C.5) becomes
![]() (C.9)
(C.9)
whereas![]() ,
, ![]() are to be converted into
are to be converted into![]() ,
, ![]() with their union being the unit disc D centered at the origin (0,0) of the x, y plane. Finally, introduce coordinates r,
with their union being the unit disc D centered at the origin (0,0) of the x, y plane. Finally, introduce coordinates r,![]() :
:
![]() (C.10)
(C.10)
r being the distance between ![]() and
and![]() , whereas the angle
, whereas the angle![]() , in radians, is an angle between vectors
, in radians, is an angle between vectors ![]() and PQ. Expression (C.9) becomes
and PQ. Expression (C.9) becomes
![]() (C.11)
(C.11)
Introduce an (acute) angle ![]() which is determined by any of the relations
which is determined by any of the relations
![]() (C.12)
(C.12)
Omitting a few more (straightforward) technicalities, we obtain
![]() (C.13,C14)
(C.13,C14)
The upper limits![]() ,
, ![]() are as follows:
are as follows:
![]() (C.15,C.16)
(C.15,C.16)
Let us conclude in terms of the following statements.
Theorem C.1. For k not equal −1, the integrals (C.2), (C.3) can be evaluated as follows:
![]() (C.17)
(C.17)
For k = −1
![]() (C.18)
(C.18)
Theorem C.2. For every integer k,
![]() (C.19)
(C.19)
Theorem C.3. For a nonnegative k, each of the integrals (C.17) is a finite linear combination of integrals![]() ,
, ![]() where
where
![]() (C.20)
(C.20)
Remark C.4. Each of the integrals (C.20) is an elementary one and it can be expressed as a polynomial in s and![]() .
.
Recall notations a, b, c, d of Section 2 (see the line prior to Formula (2.9)) for the integrals which are of our utmost interest.
Theorem C.5. The integrals a, b, c, d, are as follows:
![]() ,
,
![]()
![]() ,
,
![]()