Completing the Standard Model with Gravity by General Relativizing Quantum Physics (RQP) (Coupling Spin-2 Gravitons with Spin-0 Particles to Generate Higgs Mass) ()
1. Introduction
The overall purpose of this paper is to demonstrate a general relativistic methodology (based on a consistent- Lagrangian approach) capable of generating mass-to-spin values for elementary particles, thereby completing the Standard Model of particle physics with gravity:
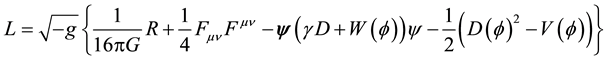 (1)
(1)
In particular, we apply a general relativistic consistency formulation to gravity―similar to James Clerk Maxwell’s consistent approach for electricity and magnetism, to precisely calculate the mass, and then spin, of the Higgs’ particle recently discovered at CERN. This approach can then be applied to any Standard Model Particles. To accomplish this in general,
1) We determine the free Lagrangian parts, for various spin particles from a group theoretical approach (not shown in this paper). Next we determine the spin interaction terms with gravity through a consistency condition (CC) first conceived by M. Fierz and W. Pauli in the 1930s, and then developed further over the next fifty years by many prominent researchers [1] -[11] (see appendices for mathematical details). This CC gravitational-spin procedure allows for the construction of the interaction Lagrangian terms, order-by-order, in flat spacetime (or in curved spacetime); moreover the CC formulation is able to test the validity of each resulting wave equation term―or the entire wave equation―(analogous to how Maxwell applied a divergence to electromagnetic equations to correct Ampere’s Law. Please note that the gravitational CC form was put into its final and complete form by J. Fang, and so is referred to as the Maxwell-Fang Consistency Condition MFCC [12] ).
2) More specifically, after varying the corrected Lagrangian for gravity interacting with spin particles, the Einstein part of the wave equation (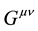 ) was separated out from the interaction spin-terms―interpreted as the spin energy momentum tensor. In this paper we focus on the spin-0 particle interacting with gravity. Upon applying the MFCC approach to spin-0 particles interacting with gravity, it produced the following general relativistic wave equation:
) was separated out from the interaction spin-terms―interpreted as the spin energy momentum tensor. In this paper we focus on the spin-0 particle interacting with gravity. Upon applying the MFCC approach to spin-0 particles interacting with gravity, it produced the following general relativistic wave equation:
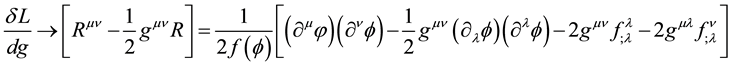 (2)
(2)
3) Having calculated the spin-2, coupled to spin-0 covariant wave equation, we next considered the wave equation in flat spacetime (negligible spin-0 particles present). This allowed us to temporarily switch off the interaction terms on the right-hand-side of the equation, representing interaction with gravity (i.e. the energy momentum tensor for spin-0 particle interaction with gravity).
4) Having determined the interaction Lagrangian (where it structurally expresses spin-0, but not particle mass), we then produce this same energy momentum tensor Tμν from a secondary approach (This energy momentum tensor turns out to be n-valued). To accomplish this secondary equivalent tensor, we evaluate Einstein’s wave equation: , in flat spacetime, but specifically at the microscopic level where va-
, in flat spacetime, but specifically at the microscopic level where va-
cuum energy fluctuations induce graviton oscillations. This means at the local level, spacetime is no longer Minkowski, and requires construction of a modified flat-spacetime-metric based on a field of oscillating gravitons (as we shall discuss in some detail in subsequent sections).
After a straightforward general relativistic calculation on the modified flat spacetime metric, a pair of n-va- lued covariant and contravariant energy momentum tensors emerged analogous to quantum raising and lower operators. Since General Relativity, in its essence, is a mass-energy covariant theory, and its metric constructed upon fluctuating vacuum energy, the resulting n-valued energy operators Tμν, is expected to generate Standard Model particle mass (in this paper the boson mass-energy), which turns out to be the case. Consequently, when the interaction terms (ghostly-coupled to ) were switched back on in a region rich in the spin-particles, the n-valued operators Tμν correspondingly became elevated in energy and in turn could generate fundamental particle mass. Then by equating the two energy momentum tensors, allowed us to couple spin-to-mass [13] .
) were switched back on in a region rich in the spin-particles, the n-valued operators Tμν correspondingly became elevated in energy and in turn could generate fundamental particle mass. Then by equating the two energy momentum tensors, allowed us to couple spin-to-mass [13] .
What must be made clear here, is, that flat spacetime at the microscopic level (represented by a modified flat-spacetime metric gμν) can be energized (massless gravitons into massive n-valued ones, which then decay, releasing their n-valued gravitational energy into the vacuum energy to generate fundamental particles with definitive mass and spin (if this gravitational energy is not absorbed by vacuum energy, then it expands outward, causing accelerated spacetimes). The lower bound mass for any fundamental particle, can is easily be calculated from the covariant and contravariant energy momentum tensors Tμν, when n = 1. For the upper bound particle mass, we expect the n-value to be close to the ground state mass (n = 1). Moreover though not yet completely understood, the spin number of the each Standard Model particle must also restrict what n values may be generated to produce the various fundamental particle masses. Hence the mass hierarchal problem coupled to spin is solved in large part.
5) As an example to what we are expressing in this manuscript, we will first determine boson mass, (including Higgs) from the n-valued energy momentum operators (decoupled from the general relativistic wave equations and transported into extreme spacetimes where these operators can be excited into higher n-states). Once boson mass is calculated, the next step is to determine the energy momentum tensor in a second way via the Maxwell-Fang Consistency Formulation (MFCC). The first method provides the fundamental mass of the Standard Model particles, the second the spin of these particles coupled to gravity. Since these terms represent, in effect, the same energy momentum tensor, we simply set them equal, thereby forming equation that correlates spin-to-mass of all Standard Model particles; however we will focus exclusively on spin-0 particles coupled to gravity.
Some of the preceding ideas were formulated from Fronsdal and Fang ideas developed from a Gupta program: “The only naturally available symmetric, divergence free source is the total energy-momentum tensor of a closed system of fields, such as the fields of Maxwell-Dirac electrodynamics. But such a system ceases to be closed the moment it provides the source for our spin-2 field, unless it includes the spin-2 field itself. Therefore we must replace the external source t by t + δt, where δt is the energy-momentum tensor of the spin-2 field.”
6) Overall, the preceding results fulfill Einstein’s vision of showing quanta arising from the gravitational field equations [14] [15] . On the other hand, this would not have been possible without the development of the Standard Model of particle physics.
2. Mathematical and Physical Development of the Modified Flat Spacetime Metric
Part of this section (and part of others) was developed in our previous paper [16] ; its mathematics is essential in understanding the overall approach taken in this paper, which is to complete the Standard Model of particle physics by advancing the Higgs boson concept into a full general relativistic framework (well-beyond the Mexican hat explanation). This is done through the concept of fluctuating vacuum energy inducing graviton oscillations in the general relativistic wave equations.
Our goal in this section is to construct a modified flat spacetime metric at the microscopic level, where vacuum energy fluctuations induce graviton oscillations. Under such a general relativistic scenario, no longer is spacetime Minkowski:
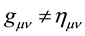 (3)
(3)
Instead, we construct a spacetime metric based on graviton oscillations induced by vacuum energy fluctuations. Our mathematical starting point is to apply the classical Lagrangian representing a vibrating system of particles about a point of equilibrium:
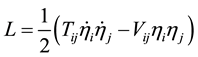 (4)
(4)
The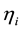 ’s represent small deviations from the generalized coordinates
’s represent small deviations from the generalized coordinates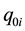 , and expressed by the equation:
, and expressed by the equation: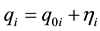 . The
. The ’s subsequently become the generalized coordinates for the equations of motion, wherein the kinetic energy has only diagonal components:
’s subsequently become the generalized coordinates for the equations of motion, wherein the kinetic energy has only diagonal components:
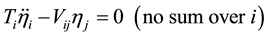 (5)
(5)
The solution to this equation has the form of normal coordinates [17] given by:
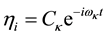 (6)
(6)
To simplify matters, and for purposes of clarification, let the coefficients 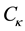 be set equal to one, also let negative one-half be introduced into the natural exponent. These small changes allow for the physics―the motion and energy of gravitons undergoing oscillations―to become mathematically and physically apparent [Of notable importance, should the resulting covariant and contravariant energy momentum tensors―calculated from the modified flat spacetime metric―be in accordance with the vibrational motion of the gravitons that we imagined flat spacetime to be undergoing, it will further substantiate the approach taken in this paper. After a straightforward, but lengthy, general relativistic calculation, this turns out to be the case, refer to our previous paper.
be set equal to one, also let negative one-half be introduced into the natural exponent. These small changes allow for the physics―the motion and energy of gravitons undergoing oscillations―to become mathematically and physically apparent [Of notable importance, should the resulting covariant and contravariant energy momentum tensors―calculated from the modified flat spacetime metric―be in accordance with the vibrational motion of the gravitons that we imagined flat spacetime to be undergoing, it will further substantiate the approach taken in this paper. After a straightforward, but lengthy, general relativistic calculation, this turns out to be the case, refer to our previous paper.
Next we apply Rayleigh’s principle [18] [19] to the coordinate frequencies 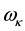 to reduce them to their fundamental mode of oscillation ω having the greatest intensity. This implies the average kinetic energy
to reduce them to their fundamental mode of oscillation ω having the greatest intensity. This implies the average kinetic energy 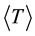 becomes equal to the average potential energy
becomes equal to the average potential energy![]() . Joining these normal coordinate concepts together, allows us to construct a basis for the general relativistic coordinate system; moreover it allows computation of the modified flat-spacetime-metric (representing graviton oscillation):
. Joining these normal coordinate concepts together, allows us to construct a basis for the general relativistic coordinate system; moreover it allows computation of the modified flat-spacetime-metric (representing graviton oscillation):
![]() (7)
(7)
We introduce the ![]() into the natural exponent for physical and mathematical reasons:
into the natural exponent for physical and mathematical reasons:
![]() (8)
(8)
At first we did not understand the importance of placing the ![]() into the spacetime metric; that occurred later when we observed the contravariant energy momentum tensor undergoing cyclic phasing from real to imaginary energies, as a function of n.
into the spacetime metric; that occurred later when we observed the contravariant energy momentum tensor undergoing cyclic phasing from real to imaginary energies, as a function of n.
In closing this section we mention that when: n = 0, or when ![]() (where m and n are natural numbers), the modified flat-spacetime metric reduces to Minkowski, implying flat spacetime-nodes dynamically appear throughout the cosmos. Hence particle physics at its foundation, is a massless continuous spacetime theory, joined discretely to a massive one having certain de Broglie wave-like characteristics.
(where m and n are natural numbers), the modified flat-spacetime metric reduces to Minkowski, implying flat spacetime-nodes dynamically appear throughout the cosmos. Hence particle physics at its foundation, is a massless continuous spacetime theory, joined discretely to a massive one having certain de Broglie wave-like characteristics.
3. Energy Operators from Pure Gravity
After acting on the modified flat spacetime metric with the Einstein Tensor Gμν, it leads directly to the following energy momentum tensors:
![]() (9)
(9)
![]() (10)
(10)
We now assume these operators can be detached from the general relativistic field equations, without losing their structural integrity, or energy-relationship to the spin-0 interaction terms that were previously switched off. Once the spin is switched back on, this allows fundamental particle mass to gain spin. Physically, this is accomplished by transporting the covariant and contravariant energy momentum tensors to regions of spacetime, which are rich in the particular spin-particle.
In closing this section, we note that the covariant and contravariant energy momentum tensors are related via raising and lowering properties of the spacetime metric:
![]() (11)
(11)
Since the covariant tensor is completely real, and the contravariant tensor complex, (each contributing to fundamental particle mass), yet both tensors are acting on the same point in spacetime, this suggests a superposition principle for spacetime itself. Moreover, it offers an explanation as to why ordinary matter dominates in the universe. Finally we note that the two energy tensors obey conservation of energy.
![]() (12)
(12)
Under MFCC, this implies the modified flat spacetime metric developed in this paper, and resulting energy momentum tensors, are consistent and valid, in the same way as were the electromagnetic equations made consistent, (and a correct and beautiful expression of nature), after James Clerk Maxwell added a single term to Amperes’ law.
4. Boson Mass Calculations
In this section we calculate the boson masses for the time component of the energy momentum operators:
![]() (13)
(13)
Part of this section was developed in our previous paper; the reader may refer to that paper for clarification and details. From the covariant and contravariant energy momentum tensors, and number density of particles approximated in extreme spacetimes (near black holes), we calculate the energy per particle:
![]() , (14)
, (14)
![]() (15)
(15)
where ![]() is the graviton angular frequency calculated in our precursor paper [20] :
is the graviton angular frequency calculated in our precursor paper [20] :
![]() (16)
(16)
with ![]() and
and![]() . This is the base energy in the creation of both the mass and spin of a particle formulated from the General Theory of Relativity. By dividing this energy by Planck’s constant will provide us with the energy-to-spin ratio necessary to not only generate mass but the spin of all particles (including spin-0 Higgs particle.
. This is the base energy in the creation of both the mass and spin of a particle formulated from the General Theory of Relativity. By dividing this energy by Planck’s constant will provide us with the energy-to-spin ratio necessary to not only generate mass but the spin of all particles (including spin-0 Higgs particle.
![]() (17)
(17)
This is the fundamental spin-mass frequency required to generate massive particles from excited gravitons releasing their gravitational energy into the vacuum energy. This associated wavelength is:
![]() (18)
(18)
Equation (18) is in the gamma ray range. We might therefore expect to find gamma rays produced in extreme spacetimes, and in the hottest and most energetic objects in the universe, where the energy momentum operators reflect elementary particle creation and annihilation. For example with neutron stars, pulsars, supernova explosions, and regions around black holes. On Earth, gamma waves are generated by nuclear explosions, lightning, and the less dramatic activity of radioactive decay―which suggests that graviton excitation and elementary particle creation is gravitationally involved in formation of the strong force.
Next we convert the energy operators T00 into mass generators:
![]() (19)
(19)
![]() (20)
(20)
Applying superposition to the two mass generators, we are able to generate the n-valued boson masses. We calculate the W-boson mass first, by setting n = 7, for the covariant mass, and n = 30 for the contravariant mass. This leads to the following bosonic results:
![]() (21)
(21)
The contravariant mass is calculated to be:
![]() (22)
(22)
Adding the generated masses together yields the theoretical W-boson mass value of:
![]() (23)
(23)
Comparing the theoretical W-boson mass to the empirically measured mass of 80.403(29) GeV/c2, as reported in CODATA [21] , (converted to SI units via:![]() ), leads to a CODATA W- boson mass of:
), leads to a CODATA W- boson mass of:![]() . Indeed, the theoretical and empirical W-boson mass value are in precise agreement.
. Indeed, the theoretical and empirical W-boson mass value are in precise agreement.
Next we compute the Z0 boson mass by setting n = 1 for the covariant operator and n = 32 for the contravariant operator.
![]() (24)
(24)
![]() (25)
(25)
Combining the n-valued masses, we have:
![]() (26)
(26)
This mass value is in precise agreement with the CODATA (2013) report on the Z0 boson mass value of: 91.1876(21) GeV/c2 (1.6255(66) × 10−25 kg). Again theoretical and empirical particle mass values are in strong agreement.
Finally, we compute the Higgs mass by selecting n = 32 for the covariant contribution, and n = 37 for the contravariant mass contribution:
![]() (27)
(27)
The contravariant mass contribution is given by:
![]() (28)
(28)
Combining these two masses via superposition of the two energy operators, we determine the theoretical mass value for the Higgs-boson:
![]() (29)
(29)
The mass result for the Higgs particle is in precise agreement that reported by CERN 2.246153925 × 10−25 kg [22] .
We have shown for the W-boson mass, n takes on the values of n = 7 for the covariant mass, and n = 30 for the contravariant mass. Similarly, for the Z0 boson mass, n takes on the value of n = 1 and n = 32. Finally for the Higgs boson particle mass, n = 32 for the covariant contribution and n = 37 for the contravariant contribution. We now see that the general relativistic wave equations, representing gravitons interacting with the vacuum energy, produce fundamental boson masses, from a very restricted range of n-values, as predicted.
5. Mass-Spin from Space-Time
In this section, we forge elementary particle mass to its spin, thereby solving the mass hierarchal problem, providing physical explanation beyond group theory, as to why elementary particle mass has its associated spin value. To demonstrate this approach, we chose the spin-0 particle. We begin by calculating the variation with respect to each particle field:
![]() (30)
(30)
![]() (31)
(31)
Applying this equation in flat spacetime, we can switch off the spin-0 interaction terms and replace ![]() by its equivalent operator form:
by its equivalent operator form:
![]() (32)
(32)
This implies we can precisely predict the spin-0 particle energies and masses by substituting this last result into the previous:
![]() (33)
(33)
As we previously showed (boson mass calculations), we could convert these two operators into mass covariant and contravariant mass generators to determine the n-valued boson masses. In particular by setting n = 32 for in covariant generator, and n = 37 for the contravariant mass generator, we were able to calculate the Higgs boson mass:
![]() (34)
(34)
The contravariant mass contribution is given by:
![]() (35)
(35)
Combining these two masses via superposition of the two energy operators, yields the theoretical Higgs-boson mass in precise agreement as reported by CERN of 126.0 GeV or 2.246153925 × 10−25 kg:
![]() (36)
(36)
Though further investigation is needed, this last Higgs result implies we may eliminate the potential function: ![]() shown in equation [1] .
shown in equation [1] .
Inclosing this section, out of respect we refer to various fundamental particles (including Higgs) generated from MFCC and RQP theory, as Veltman and t’Hooft elementary particles [VHP].
6. Conclusions
Though not well-known, it was Einstein who first endeavored to manifest quanta from his gravitational field equations (rather than quantizing gravity). By elevating the Standard Model into a general relativistic framework, it was shown in this paper that such mass-energy quanta were indeed generated in correspondence with their elementary particle spin values. It is important to note that the Relativized Quantum Physics approach (RQP) applied in this paper is a massless field approach discretely coupled with a massive one; consequently it overcomes various renormalizing difficulties. Furthermore, by applying a similar consistency approach to the gravitational field equations, as Maxwell did to the electromagnetic ones, we were able to couple spin-to-mass, thereby restricting the particle mass in precise agreement with experimental values. Moreover this approach in theory solves the mass hierarchal problem of the Standard Model of particle physics (and verified empirically for three boson masses), implying quantum physics is a subset of General Relativity, as first imagined by Einstein. We have shown for boson mass the n-values do not exceed n = 37 for the upper limit mass, and has a lower limit mass n = 1. To make RQP theory a massless theory, we simply set n = 0. Antiparticle masses may be achieved by setting “n” to negative integer values.
In the future we hope to apply the RQP method to determine all elementary particle mass and spin.
Acknowledgements
I wish to express my respect and thanks to the Chinese People―dream to dare. With appreciation, I wish to genuinely thank Gerard t’Hooft for choosing me to peer review for Foundations of Physics. Gerard t’Hooft is one of the few physicists who makes complete, absolute, clear, sense when discussing fundamental nature―even when others are unable to follow along.
Appendix I: Maxwell’s Consistency Approach
Rather than starting with the four electromagnetic field equations, as Maxwell did, we begin from the modern approach of the action S, where:
![]() (37)
(37)
Here, L represents the Lagrangian density for any system under consideration. Specifically, the Lagrangian for electromagnetic fields interacting with matter, and is given by:
![]() (38)
(38)
Identical indices are understood to be summed. The free part of the Lagrangian density (self -interaction) is given by:
![]() (39)
(39)
The interaction Lagrangian density term is given by:
![]() (40)
(40)
[Note: Only partial derivatives are being used here. Also keep in mind the structure of the Lagrangian is a scalar product of the electromagnetic field Aμ with the electric current density jμ. In a like manner our interaction Lagrangian for gravity under CC considerations will have the gravitational field coupled to its source.]
The Euler-Lagrange equations of motion, for an arbitrary field component ϕ, is given by1:
![]() (41)
(41)
Substituting Lem into the Euler-Lagrange equation of motion, yields the four well-tested Maxwell’s electromagnetic equations:
![]() (42)
(42)
The above result is key to our understanding of how to build a consistent field theory for gravity. By examining the left hand side of this divergent equation, we see it is simply the equation of continuity and must physically, as well as mathematically, equal zero (unless conservation of charge fails). The right hand side of the equation is designed so that the terms Aμ, in the equation of motion, have zero divergence identically (this requirement will also be fundamental to the CC gravitational approach, and though a gauge approach may yield a similar result, it does not do so as viscerally and so we are not led to the correct theory for gravity and dark matter). Hence, we have shown the electromagnetic field equations are consistent.
Appendix II: Maxwell-Fang Consistency Approach
If we are to build any viable theory in physics, its foundation must be based on those successful traditions from both physics and mathematics. For example, the ideas for special relativity were established when young Einstein considered the consequences of James Clerk Maxwell’s electromagnetic equations from various inertial coordinate frames. Likewise, to build a consistent theory for gravity, we again turn to the seminal work of James Clerk Maxwell, in which he demanded the divergence of the source for electromagnetism equal zero. That is: jμ,μ = 0; which led to the discovery of the composition of light. By this successful example, we too will require the divergence of the source for gravity-the energy momentum tensor (Tμν) equals zero:
![]() (43)
(43)
However, a consistent theory for gravity is not as straightforward as it was for the electromagnetic equations. For one thing, gravity interacts with itself. Not only this, but the source for gravity includes a variety of other sources beyond current density, such as: mass-energy, momentum and radiation (just to name a few). In short, Maxwell’s consistent condition points us in the right direction, but needs modifications if we are to produce an analogous theory for gravity. So what then is the next step? Since we are seeking a gravitational approach, our theory has to be constrained by Einstein’s requirement that the gravitational field ultimately must have a geometrical interpretation. Fortunately, R. Feynman showed the gravitational equations of motion, obtained from flat spacetime, from an action principle on the Lagrangian, is equivalent to Einstein’s geometric requirement2.
Developing a theory for pure gravity is one thing, but what do we do when gravity interacts with matter? In theory, one could build infinitely many Lagrangians, but which of them would represent real nature? Especially when there are so many particles that were not even known during the development of general relativity? The answer is to continue on with the modern approach to gravity through linearization of the gravitational field [23] , and to treat gravity as a spin-2 particle hμν (graviton). And that is just what occurred historically, until R. Feynman imposed that the interaction Lagrangian represent a coupling to gravity in the following manner:
![]() (44)
(44)
From the form of the coupling above, the gravitational field, hμν must be symmetric on μν. The scalar product of the anti-symmetric part of hμν with symmetric tensor Tμν is then zero, implying that the anti-symmetric part of hμν would not couple to matter and therefore never be seen. The full Lagrangian for gravity proposed by Feynman is composed of the free part Lg, as well as the interaction Lagrangian. That is:
![]() (45)
(45)
The Euler-Lagrange equations of motion for gravity are then given by:
![]() (46)
(46)
To have the same type of consistency for the gravitational field equations, as with the electromagnetic field equations, Feynman demanded that the divergence of the free part of the Lagrangian equals zero; that is:
![]() (47)
(47)
This automatically forces the divergence of interaction part of the Lagrangian to be zero; otherwise the total divergence of Einstein’s field equations would not equal zero, implying we would lose any sense of conservation of the source. This leads us to the founding principle for gravity:
![]() (48)
(48)
In terms of the consistency formulation, the gravitational field equations must satisfy the condition:
![]() (49)
(49)
Conceptually this gravitational condition on the field equations, is no different to the consistent formulation imposed on the electromagnetic equations by James Clerk Maxwell.
From the proceeding we develop a general consistent approach for gravity.
Here we provide additional information about the consistency formulation for particle fields interacting with gravity first developed by M. Fierz and W. Pauli in the 1930’s. Based on their seminal work, subsequent researchers (all luminary) contributed to the gravitational consistency formulation. Then after R. Feynman work in this field in the 1960’s, the consistency formulation was put into its final and complete form by J. Fang. In this paper we refer to this gravitational consistency formulation interacting with all particle fields, as the Maxwell-Fang consistency condition (MFCC). The main condition of Fang’s consistency condition, is that the divergence of the wave equation must equal zero; not identically, nor by particular solutions, but rather by collecting various divergent terms into numerous forms of the wave equations, and then setting them all to zero. Only in this way can the correct Lagrangian (leading to a set of consistent set of field equations for gravity) be determined. Schematically, the consistency condition is written as a variation on the Lagrangian followed by a divergence on the field equations:
![]() (50)
(50)
To understand the basic idea behind the consistency condition formulation for linearized gravity, let us consider a system of coupled fields, Φ, under variation given by:
![]() (51)
(51)
Let the subset Φ’ be that of the massless gauge fields. Such field equations can always be decomposed into linear (L) and nonlinear (NL) parts, in which variation of the fields, yields:
![]() (52)
(52)
For reasons previously given, the divergence of linear part of the wave equation must equal zero:
![]() (53)
(53)
The above condition, together with gauge invariance, imposes a strict requirement on the nonlinear parts, so that the divergence must also equal zero (otherwise the field equations would be inconsistent mathematically):
![]() (54)
(54)
It was J. Fang, who first understood that the nonlinear divergence can go to zero in three distinct ways:
1) The divergences on the nonlinear parts of the massless gauge field equations are zero identically (that is they vanish as mathematical identities-without referring to the field equations). However, such an approach provides no physical content.
2) The divergences of the nonlinear parts of the massless gauge field equations are zero neither identically, but only analytically for some particular solutions (not general enough), which happen to satisfy the consistency condition:
![]() (55)
(55)
3) The divergences of the nonlinear parts of the massless gauge field equations are equal to the sum of various terms, where each of these is proportional to the original field equations or various contracted field equations. Therefore, the divergence of the nonlinear parts of the massless gauge field equation vanish by field equations, and is expressed mathematically by:
![]() (56)
(56)
where A, B, C are some structure functions for the field equations, or for various contracted field equations (trace, differentiation, etc.), which could depend on the field Φ itself, and derivatives of the fields.
Let us reexamine the three cases above more carefully: Case (1) is simply too strong a condition and must rejected because it would exclude many well established theories such as electrodynamics; SU (2) Yang-Mills gauge theory and Einstein’s theory of gravitation. Case (2) is not general enough to provide criteria for constructing the Lagrangian describing gravity coupled to particles of various spin; and so case (2) is also rejected. Case (3) has just the right condition to allow one to build up the Lagrangian order-by-order in flat spacetime representing the gravitational system. This same criteria may also be applied to curved spacetime to determine if the chosen Lagrangian produces inconsistent field equations. Furthermore, case (3) has been shown to be compatible with other established theories, such as general relativity; Scherk-Schwarz dual model for string theory and Yang-Mills theory. Finally, it allows the massless gauge fields Φ’ to maintain the freedom of the deformed gauge transformation:
![]() (57)
(57)
where χ stands for a set of gauge parameters, which are a function of xμ. And Γ is some structure function. Thus the gauge is modified, but not lost.
Instead of using Case 3 in the given form and postulating the structure functions A, B, C, ∙∙∙ , it is more feasible, and equivalent, to use the consistency condition (CC) in the form:
![]() (58)
(58)
where δL/δΦ = 0 represents the set of all field equations and δL/δΦ’ = 0 refers only to the subset of field equations for Φ’ that are massless gauge fields. In this approach, the nonlinear part of the Lagrangian of the system L(Φ) is the yet-unknown Lagrangian to be determined by CC. Whereas, the lowest order term in L(Φ) is the usual Fierz-Pauli type free-field Lagrangian constructed from the standard group theoretical approach [24] .
Although other attempts at a consistency formulation are valid, without Fang’s subtle understanding and completion of the consistency formulation, all previous attempts are incomplete and so lead to Lagrangians that, in general, inaccurately represent real nature.
Appendix III: MFCC Example
In this section we provide an example of how the Maxwell-Fang Consistency Condition (MFCC) can generate String Theory (Scherk and Schwarz), both on flat and curved spacetime.
How exactly then does a flat spacetime approach work to determine the Lagrangian for some unknown system of spin particles interacting with gravity? In particular, for the spin-0 (2-form) particles denoted by “a”, interacting with gravitational spin-2 particles, denoted by “h”, described by dual-string model Lagrangian. We begin by forming all possible combinations of the two fields up to third expanded order. Symbolically this is written as:
![]() (59)
(59)
The metric is expanded as:
![]() (60)
(60)
Here ![]() is recognized as flat spacetime or Minkowski metric, and
is recognized as flat spacetime or Minkowski metric, and ![]() represents the graviton field. Note, that any derivatives on the expanded metric gμν leaves only derivatives of
represents the graviton field. Note, that any derivatives on the expanded metric gμν leaves only derivatives of![]() . Variation on the linearized Lagrangian up to third order, with respect the spin-0 field “a” (two-form) and spin-2 fields “h”, is given by:
. Variation on the linearized Lagrangian up to third order, with respect the spin-0 field “a” (two-form) and spin-2 fields “h”, is given by:
![]() (61)
(61)
![]() (62)
(62)
The variation produces the linearized wave equation with both correct and incorrect terms. To get rid of the unwanted terms, or to show the Lagrangian is already correct, the next step of the consistency condition is to take the divergence of the wave equation. Then terms are grouped together in such a way as to form structures of the wave equation. By the consistency condition these grouped wave equations are set to zero. The remaining terms must cancel algebraically. If this occurs, then the order-by-order Lagrangian correctly represents gravity interacting with particles. If not, terms must be added to make this main condition of CC hold. This is exactly what was done with a general form of a Lagrangian representing spin-0 particles interacting with gravity. Note this is not yet the Scherk-Schwarz dual model Lagrangian. However, without prejudice, we discovered (after many pages of calculations), the dual-string Lagrangian was sifted out via CC. To show this, we choose for the sake of the reader to develop a schemata that indicates what occurs to various Lagrangian terms. Note that we use unspecified coefficients to produce the most general Lagrangian. Part of the consistency condition is to solve for these coefficients up to a single coefficient, which can only be determined experimentally. Put another way, mathematics alone cannot yield the values to fundamental constants.
The CC applied to spin-0 particles interacting with spin-2 graviton particles, is given in schemata form, where each interaction and free Lagrangian term ![]() is shown under the CC term to either go to zero or not. If it goes to zero it is not a correct expanded Lagrangian term:
is shown under the CC term to either go to zero or not. If it goes to zero it is not a correct expanded Lagrangian term:
![]() (63)
(63)
![]() (64)
(64)
![]()
Hence L(a2∙h) reduces to:
![]() (65)
(65)
Please note this third order Lagrangian term has been reduced to a single coefficient a10, and is thus a valid Lagrangian term. The remaining third order interaction Lagrangian is examined under CC and field redefinition FR. The result shows this interaction Lagrangian is not allowed. Under CC schemata this is shown as follows:
![]() (66)
(66)
The consistency condition, with field redefinition, has revealed that L(a∙h2) does not partake in gravity interacting with spin-0 particles.
Finally, to clarify what is meant by field-redefinition (FR) in the schemata immediately above, is to say that two infinite series polynomial type Lagrangians: L({a}∙Φ) and L({b}∙Φ), having the same linear parts but each containing a different set of free parameters {a} and {b} specifying their non-linear parts, are regarded as completely equivalent if L({a}∙Φ) transforms into L({b}∙Φ) under field redefinition FR:
![]() (67)
(67)
Here the polynomial {c∙Φ∙Φ} contains terms from all possible combinations contracted out of any two fields in Φ, without derivatives. The most general form of FR for the case above is as follows:
![]() (68)
(68)
![]() (69)
(69)
Dual tensors, like εμνλσ aλσ h and εμνλσ (aλκaσκ ? aσκhλκ) are allowed for, but not included here because of their odd parity under space inversion.
Appendix IV: String Theory in Curved Spacetime MFCC Approach
In this section we show the Scherk-Schwarz Lagrangian satisfies the consistency condition in curved spacetime. This is a two-step procedure: 1) Variation of the Lagrangian with respect to each of the fields {gμν, aμν, ϕ}, thereby generating three distinct wave equations. 2) Apply the divergence to each of these wave equations, and show they equal zero; if so we have correct gravitational theory, just as we have shown with theory.
Step 1) Rather making many tedious variational calculations with full covariant derivatives, we simply show the final result of the dual-string wave equations:
![]() (70)
(70)
![]() (71)
(71)
![]() (72)
(72)
The constant “a” equals 1/6 and F2 is given by:
![]() (73)
(73)
Step 2) Apply the divergence to these wave equations and show they equal zero:
![]() (74)
(74)
Note the two terms are the free part of the gravitational field and the interactions terms, which is also the energy momentum tensor. Let us now expand the right hand side to make more visible the divergence.
![]() (75)
(75)
By analogy to the electromagnetic equation, the divergence of the free part of the wave equation must vanish, hence:
![]() (76)
(76)
What is then left is to show that the divergence of the interaction part of the wave equation, vanishes as well:
![]() (77)
(77)
For the Scherk-Schwarz dual model, the divergence of the interaction terms (which are really the energy momentum tensor) must vanish. Hence:
![]() (78)
(78)
After bringing in the covariant derivative with respect to “ν,” and then cancelling hundreds of terms algebraically, as well as setting divergent structures of the wave equation to zero (main CC requirement to be given further discussion), we discover, indeed, the divergence of the interaction terms, that is, the divergence of the energy momentum tensor for the Scherk-Schwarz string theory, does indeed go to zero. Then, by the same assumption made by J. Maxwell, R. Feynman, and then J. Fang, the Scherk-Schwarz Lagrangian representing spin-0 particles interacting with gravity produces consistent field equations. This means the dual string model is a viable representation of nature; however, nature is the final judge.
Appendix V: Identities from the Maxwell-Fang Consistency Formulation
During the development of QED, at first there were many infinities that could not be mathematically accounted for until Feynman absorbed some of these infinities into the mass and charge. Nevertheless it was not until the Ward-Takahashi identity [25] was developed, did QED become a renormalizable theory. The Ward-Taka- hashi identity is a quantum version of the classical Noether’s theorem. Recall previously in this paper, T. Yoneya [26] discovered that all the known string theories included a massless spin-two particle, which obeyed the correct Ward identities. Other examples exist, such as the identities associated QED and Einstein’s gravity, respectively:
![]() (79)
(79)
And
![]() (80)
(80)
In our paper the consistency condition produces to new identities. One identity associated with the Callan- Coleman-Jackiw Lagrangian corresponding to the massless gauge field![]() . And two identities associated with the Scherk-Schwartz Lagrangian corresponding to the two fields
. And two identities associated with the Scherk-Schwartz Lagrangian corresponding to the two fields ![]() and
and![]() . For the Callan-Coleman- Jackiw Lagrangian we define the following symbolism in order to present the associated identity in compact notation:
. For the Callan-Coleman- Jackiw Lagrangian we define the following symbolism in order to present the associated identity in compact notation:
![]() (81)
(81)
The field equations generated from this Lagrangian are given as follows:
![]() (82)
(82)
![]() (83)
(83)
And the energy momentum tensor is given by:
![]() (84)
(84)
![]() (85)
(85)
![]() (86)
(86)
After a lengthy calculation the generalized Fang identities for the Callan-Coleman-Jackiw Lagrangian [27] is given as:
![]() (87)
(87)
Note that all the terms on the right-hand side of the identity involve the field equations. For the Scherk- Schwarz Lagrangian again we define the following symbolism:
![]() (88)
(88)
The Scherk-Schwarz field equations are as follows:
![]() (89)
(89)
And
![]() (90)
(90)
The Fang current density for the Scherk-Schwarz Lagrangian is given by:
![]() (91)
(91)
The final identity is:
![]() (92)
(92)
NOTES
1This mathematics leading to a consistent approach for gravity was developed by E. Huggins in his dissertation see pages 8 - 10.
![]()
2The Lagrangian approach to gravity first had its origin in curved spacetime and was introduced by the eminent mathematician David Hilbert, a few days after Einstein completed his wave equations for the general theory of relativity.