Statistical Inference in Generalized Linear Mixed Models by Joint Modelling Mean and Covariance of Non-Normal Random Effects ()
1. Introduction
Generalized linear mixed models (GLMMs) are very helpful and widely used for analyzing discrete data and data from exponential family distributions. Statistical inference of GLMMs is challenging due to the incorporation of random effects, especially for example, the marginal likelihood has the form of analytical intractable high dimensional integration. The existing and popular statistical methods include: 1) analytical Laplace approximation: the uncorrelated penalized quasi-likelihood (PQL) by Breslow and Clayton (1993) [1] and correlated PQL by Lin and Breslow (1996) [2] ; hierarchical generalized linear models (HGLM) procedure by Lee and Nelder (2001) [3] ; 2) numerical technique: Bayesian approach with sampling by Karim and Zeger (1992) [4] ; MCEM algorithm by Booth and Hobert (1999) [5] ; Gauss-Hermite quadrature (GHQ) by Pan and Thompson (2003) [6] ; Quasi-Monte Carlo (QMC) and Randomized QMC method by Pan and Thompson (2007) [7] and Aleid (2007) [8] .
One common idea in above literatures is random effects in GLMMs, which represent latent effects between individuals, follow normal distribution with mean zero and identity covariance matrix. However, these assumptions are not always valid in practice because individual has its own special natures and may not be normal distributed. To address this issue, multivariate t distribution and multivariate mixture normal distribution will be assumed for random effects in GLMMs. Quasi-Monte Carlo (QMC) method through iterative Newton- Raphson (NR) algorithm solves the high-dimensional integration problem in the marginal likelihood under the non-normal assumptions.
Review of GLMMs and the marginal Quasi-likelihood will be proposed in Section 2. QMC approximation, the simplest Good Point set (square root sequence) and analytical form of maximum likelihood estimates (MLEs) in GLMMs will be discussed in Section 3. The idea of modified cholesky decomposition and joint modelling of mean and covariance structure will be explained in Section 4. In Section 5, the salamander data will be analyzed as an example under the assumption of multivariate t distribution of random effects, then simulation study with same design protocol as salamander data followed in Section 6. Discussions on the related issues and further studies are given in Section 7.
2. Generalized Linear Mixed Models
The generalized linear mixed models (GLMMs) are typically constructed by incorporating random effects into the linear predictor of a conditionally independent exponential family model (McCulloch, 2003, [9] ).
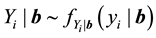 ;
;
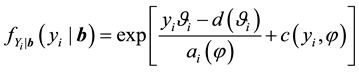 ;
;
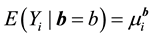 ;
;
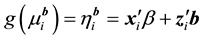 ;
;
 ;
;
where 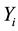 denotes the observed response,
denotes the observed response, 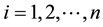 ,
, 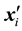 is the
is the 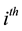 row of design matrix;
row of design matrix; 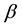 is
is 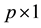 fixed effect parameter;
fixed effect parameter; 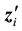 is the
is the 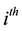 row of the second design matrix;
row of the second design matrix;  is
is 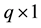 random effect.
random effect.
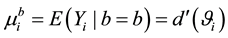 and
and![]() , where
, where ![]() is a prior weight,
is a prior weight, ![]() is a
is a
known overdispersion scalar, ![]() is the natural parameter, and
is the natural parameter, and ![]() is variance function (McCulloch and Nelder, 1989, [10] ).
is variance function (McCulloch and Nelder, 1989, [10] ).
In this definition we see the usual ingredients of a generalized linear model. First, the distribution of ![]() from an exponential family (in this case the distribution is assumed to hold conditional on the random effect
from an exponential family (in this case the distribution is assumed to hold conditional on the random effect![]() ). Second, a link function,
). Second, a link function, ![]() is applied to the conditional mean of
is applied to the conditional mean of ![]() given
given ![]() to obtain the conditional linear predictor
to obtain the conditional linear predictor![]() . When
. When ![]() is identical to the
is identical to the![]() , GLMMs is said to have canonical to link function. Finally, the linear predictor is assumed to consist of two components, the fixed effects portion, described by
, GLMMs is said to have canonical to link function. Finally, the linear predictor is assumed to consist of two components, the fixed effects portion, described by ![]() and random effects portion,
and random effects portion, ![]() , for which a distribution is assigned to
, for which a distribution is assigned to![]() . e.g. if
. e.g. if ![]() is said to follow a q-dimensional t distribution, denote by
is said to follow a q-dimensional t distribution, denote by![]() , and its density function is given by
, and its density function is given by
![]() (1)
(1)
with the mean of ![]() is
is ![]() and the covariance matrix of
and the covariance matrix of ![]() is
is ![]() respectively, where
respectively, where ![]()
is a ![]() vector,
vector, ![]() is a
is a ![]() symmetric positive definite matrix,
symmetric positive definite matrix, ![]() is the degree of freedom. If
is the degree of freedom. If ![]() is said to follow a q-dimensional mixture normal distribution F
is said to follow a q-dimensional mixture normal distribution F
![]() (2)
(2)
with mean![]() , covariance matrix
, covariance matrix ![]() where
where![]() ,
, ![]() is
is ![]() vector,
vector, ![]() is a
is a ![]() symmetric positive definite matrix.
symmetric positive definite matrix.
In GLMMs, statistical inferences of ![]() and
and ![]() are estimated in most literatures,
are estimated in most literatures, ![]() is
is ![]() fixed effect parameter,
fixed effect parameter, ![]() is a vector parameter in covariance matrix of random effect,
is a vector parameter in covariance matrix of random effect,![]() . Quasi-likelihood function of
. Quasi-likelihood function of ![]() in GLMMs is also called the marginal quasi-likelihood function which expressed by
in GLMMs is also called the marginal quasi-likelihood function which expressed by
![]() , (3)
, (3)
where
![]() ,
,
![]() , (4)
, (4)
determinates the conditional log quasi-likelihood of ![]() and
and ![]() given
given ![]() (Breslow and Clayton, 1993, [1] ).
(Breslow and Clayton, 1993, [1] ). ![]() is cumulative distribution function (CDF) of random effect b.
is cumulative distribution function (CDF) of random effect b.
It is extremely challenging to obtain the maximum likelihood estimates (MLEs), ![]() , which maximize (3) or (4). Although the integration involves an analytical expression, the computational problems are magnified when the specified model contains a large number of random effects and random effects have a crossed designed according to data description.
, which maximize (3) or (4). Although the integration involves an analytical expression, the computational problems are magnified when the specified model contains a large number of random effects and random effects have a crossed designed according to data description.
3. Quasi-Monte Carlo Integration and Estimation
3.1. Quasi-Monte Carlo Integration
Quasi-Monte Carlo (QMC) sequences are a deterministic alternative to Monte Carlo (MC) sequences (Niederreiter, 1992, [11] ). For the q-dimensional unit cube domain![]() , the Quasi-Monte Carlo approximation is
, the Quasi-Monte Carlo approximation is
![]() ,
,
where sample points ![]() should be selected to minimize the error of the integral quadrature.
should be selected to minimize the error of the integral quadrature.
If the integrand f has finite variation, then the error of the quasi-Monte Carlo quadrature can be bounded using the Koksma-Hlawka inequality
![]() , (5)
, (5)
where ![]() is variation of
is variation of ![]() in the sense of Hardy and Krause (Fang and Wang, 1994, [12] ) and
in the sense of Hardy and Krause (Fang and Wang, 1994, [12] ) and ![]() is the star discrepancy of sample points, which is a measure of uniformity of distribution of a finite point set
is the star discrepancy of sample points, which is a measure of uniformity of distribution of a finite point set![]() , defined by
, defined by
![]() ,
,
where A is an arbitrary q-dimensional subcube parallel to the coordinate axes and originating at the centre, ![]() is its volume, and
is its volume, and ![]() is the number of sample points inside this subcube.
is the number of sample points inside this subcube.
For carefully selected sample points, the discrepancy and consequently the error of low-discrepancy sequ-
ences (Niederreiter, 1992, [11] ) can be in the order of![]() , which is much better than
, which is much better than ![]()
the probabilistic error bound of Monte Carlo methods (Fang and Wang, 1994, [12] ). Moreover, quasi-Monte Carlo methods guarantee this accuracy in a deterministic way, unlike Monte Carlo methods where the error bound is also probabilistic.
In the QMC approach, there exist precise construction algorithms for generating the required points. These algorithms can be divided into two families, the Lattice rule and Digital-net. Only the good point set, which is belong to lattice rule (Fang and Wang, 1994, [12] ) will be used and discussed in following sections.
3.2. The Good Point (GP) Set
A good point![]() , where
, where ![]() is a hypercube. The set
is a hypercube. The set ![]() consists of the first K
consists of the first K
points of the set![]() , where
, where ![]() represents the fractional part of the value
represents the fractional part of the value
y. In practice, the following forms of the good point ![]() are recommended as square root sequence
are recommended as square root sequence
![]() ,
,
where![]() ,
, ![]() , is a series of prime numbers, for example, the first q primes
, is a series of prime numbers, for example, the first q primes![]() .
.
3.3. MLE in GLMMs by QMC Estimation
When QMC method applied to marginal quasi-likelihood function (4)
![]() , (6)
, (6)
where ![]() is the inverse of CDF of
is the inverse of CDF of ![]() and
and ![]() is the square root of
is the square root of![]() , for example, it can be taken
, for example, it can be taken
as the Cholesky decomposition of ![]() or eigenvalue-eigenvector decomposition.
or eigenvalue-eigenvector decomposition.
Let![]() ,
, ![]() ,
, ![]() is a good point set
is a good point set
![]() ,
, ![]() is the inverse function of
is the inverse function of![]() . The global maximum of
. The global maximum of ![]() with respect to
with respect to ![]() and
and ![]() is the solution of the score equations
is the solution of the score equations
![]() , (7)
, (7)
![]() , (8)
, (8)
where![]() ,
, ![]() is a weight for the kth point in the ith subject and it has the following form
is a weight for the kth point in the ith subject and it has the following form
![]() . (9)
. (9)
The weight ![]() given in (9) is a function of
given in (9) is a function of ![]() and
and![]() , i.e.
, i.e.![]() , which must be taken into account when calculating the second-order derivatives.
, which must be taken into account when calculating the second-order derivatives.
The score Equations (7) and (8) in general have no analytical solutions for ![]() and
and![]() . A numeral solution is given by Pan and Thompson (2007) [7] , which used Newton-Raphson algorithm.
. A numeral solution is given by Pan and Thompson (2007) [7] , which used Newton-Raphson algorithm.
![]() , (10)
, (10)
where ![]() and
and ![]() are score function of log likelihood,
are score function of log likelihood, ![]() is Hessian matrix of log like-
is Hessian matrix of log like-
lihood.
Calculation of the Hessian matrix is difficult and its computation is intensive. When the difference between ![]() and
and ![]() and the difference between
and the difference between ![]() and
and ![]() are both sufficient small, the maximum like- lihood estimates are confirmed, that is, the convergence is reached. The calculation process of Hessian matrix is given in Appendix A, which is an extension of Hessian matrix in Pan and Thompson (2007) [7] . At convergence,
are both sufficient small, the maximum like- lihood estimates are confirmed, that is, the convergence is reached. The calculation process of Hessian matrix is given in Appendix A, which is an extension of Hessian matrix in Pan and Thompson (2007) [7] . At convergence,
the MLEs, ![]() and asymptotic variance-covariance matrix of
and asymptotic variance-covariance matrix of ![]() can be obtained.
can be obtained.
4. Modified Cholesky Decomposition and Covariance Modelling for Random Effects
Modified Cholesky decomposition of![]() , rather than
, rather than![]() , and joint modelling of mean and covariance matrix were published by Pourahmadi (1999, 2000) [13] [14] , to obtain a statistically meaningful unconstrained pa- rameterization of covariance. The remarkable advantages are: 1) it guarantees covariance matrix is positive definite; 2) it reduces the number of parameters so that it makes computation efficient; 3) it has very clear statistical interpretation. The main idea of modified cholesky decomposition is that a
, and joint modelling of mean and covariance matrix were published by Pourahmadi (1999, 2000) [13] [14] , to obtain a statistically meaningful unconstrained pa- rameterization of covariance. The remarkable advantages are: 1) it guarantees covariance matrix is positive definite; 2) it reduces the number of parameters so that it makes computation efficient; 3) it has very clear statistical interpretation. The main idea of modified cholesky decomposition is that a ![]() symmetric matrix
symmetric matrix ![]() is positive definite if and only if there exist a unique unit lower triangular matrix T, with 1 as diagonal entries, and unique diagonal matrix D with positive diagonal entries such that
is positive definite if and only if there exist a unique unit lower triangular matrix T, with 1 as diagonal entries, and unique diagonal matrix D with positive diagonal entries such that
![]() ,
,
where
![]() .
.
It offers a simple unconstrained and statistically meaningful reparametrization of the covariance matrix. So ![]() and
and![]() . T and D are easy to compute and interpret statistically: the below-diagonal entries of T are the negatives of the autoregressive coefficients (ACs),
. T and D are easy to compute and interpret statistically: the below-diagonal entries of T are the negatives of the autoregressive coefficients (ACs), ![]() , in the autoregressive model.
, in the autoregressive model.
![]() , (11)
, (11)
where ![]() is a
is a ![]() number, which index the jth dimension of random effect b. That is, the linear least squares predictor of
number, which index the jth dimension of random effect b. That is, the linear least squares predictor of ![]() based on its predecessors
based on its predecessors![]() . On the other hand, the diagonal entries of D are the innovation variances (IVs),
. On the other hand, the diagonal entries of D are the innovation variances (IVs), ![]() , where
, where ![]() with
with ![]() given by (11). Obviously we have
given by (11). Obviously we have
![]() if
if ![]()
![]() . Denote
. Denote![]() . It is obvious
. It is obvious![]() , so that
, so that![]() .
.
The linear joint models of the autoregressive coefficients (ACs) and the logarithms of innovation variances (IVs)
![]() (12)
(12)
where ![]() and
and ![]() are covariates, and
are covariates, and ![]() and
and ![]() are low-dimensional parameter vectors. The choice of covariate vectors
are low-dimensional parameter vectors. The choice of covariate vectors ![]() and
and ![]() are flexible in some senses.
are flexible in some senses.
5. Salamander Data Analysis
The famous salamander interbreeding data set was published by McCullagh and Nelder (1989), which came from three repeated same protocol design experiments. The salamanders originally lived in two geographically isolated populations, Roughbutt (RB) and Whiteside (WS). Each experiment involved in two closed groups and each group involved 5 females and 5 males from each population. In a fixed period, each female mated with 6 males, 3 from each population. So 60 correlated binary observations were created in each closed group, and totally, 360 binary observations (1 for successful interbreeding, 0 for failed interbreeding) were in three ex- periments. The primary two objectives of experiment are to study whether the successful mating rate is sig- nificant between populations and if heterogeneity between individuals in the mating probability exists. This binary data set is challenging because it is block crossed, correlated, balanced (as each female mated with a total of six males and vice verse) and incomplete (as each female mated with just three out of a possible five males, and vice verse).
In a closed group, 5 females and 5 males from each population involved, so total 20 salamander were indexed by i or j. Denoting by ![]() the outcome for the mating of the ith female with the jth male, the logit mixed model for each experiment
the outcome for the mating of the ith female with the jth male, the logit mixed model for each experiment
![]() , (13)
, (13)
where the conditional probability ![]() is used to model the correlated binary responses.
is used to model the correlated binary responses.
![]() , (14)
, (14)
![]() if the
if the ![]() female comes from WS, otherwise 0. Similarly,
female comes from WS, otherwise 0. Similarly, ![]() if the
if the ![]() male comes from WS, otherwise 0.
male comes from WS, otherwise 0.
Here the random effect is not assumed as normal distribution but multivariate t distribution with degree of freedom![]() ,
,![]() .
.
Note that each experiment includes two closed groups and involves 40 salamanders so that the log-likelihood for each experiment involves a 40-dimensional integrals. The dimensionality for each experiment can be further reduced to the sum of two 20-dimensional integrals due to the block design of two closed groups, see Karim and Zeger (1992) [4] and Shun (1997) [15] for more details about the design. When the three experiments data are pooled as in model (13), the log-likelihood ![]() is a sum of six 20-dimensional integrals so that the MLEs of the fixed effects
is a sum of six 20-dimensional integrals so that the MLEs of the fixed effects ![]() and variance components
and variance components ![]() become extremely difficult to obtain.
become extremely difficult to obtain.
Modelling ![]() for salamander mating data,
for salamander mating data, ![]() ,
, ![]() and
and![]() . The autoregressive coefficients (ACs) model is reordered as
. The autoregressive coefficients (ACs) model is reordered as
![]() ,
,
where ![]() is a
is a ![]() vector,
vector, ![]() is a
is a ![]() matrix,
matrix, ![]() is the
is the ![]() row of
row of![]() ,
,![]() .
.
![]() ,
,
where
![]() ,
,
![]() if
if ![]() and
and ![]() salamander come from different genders, otherwise 0. Similarly,
salamander come from different genders, otherwise 0. Similarly, ![]() if
if ![]() and
and ![]() salamander come from different districts (populations), otherwise 0.
salamander come from different districts (populations), otherwise 0.
The logarithms of innovation variances (IVs) model is
![]()
where ![]() is a
is a ![]() matrix,
matrix, ![]() is a
is a ![]() vector,
vector, ![]() describes the variance of the
describes the variance of the ![]() sala- mander
sala- mander
![]() ,
,
where![]() , if the
, if the ![]() salamander is female, otherwise 0. Similarly,
salamander is female, otherwise 0. Similarly, ![]() if the
if the ![]() sala- mander comes from WS, otherwise 0.
sala- mander comes from WS, otherwise 0.
In the logarithms of innovation variances (IVs) model, originally there were 4 covariates including the item ![]() with interaction parameter
with interaction parameter![]() . But the results showed that
. But the results showed that ![]() approximately equals zero and has smaller order of magnitude than
approximately equals zero and has smaller order of magnitude than ![]() and
and![]() . The hypothesis test also showed that there is no evidence to reject
. The hypothesis test also showed that there is no evidence to reject![]() .
.
The salamander data is now analyzed by using QMC approach to calculate the MLEs of the fixed effects and variance components involved in the model. Specifically, we implement the simplest QMC point, square root sequences to estimate the parameters for the modelling of the pooled data. A set of 20-dimensional points on the unit cube ![]() were generated for the six 20-dimensional integrals. Then the points are modified
were generated for the six 20-dimensional integrals. Then the points are modified
through using transformation, ![]() , where
, where ![]() is the cumulative distribution function of the multi-
is the cumulative distribution function of the multi-
variate t distribution, ![]() is the modified Cholesky decomposition for
is the modified Cholesky decomposition for![]() . After that, we approxi-
. After that, we approxi-
mate the integrated log-likelihood, then we use the Newton-Raphson algorithm (10) to maximize the appro- ximated log-likelihood function.
The covariance modelling for![]() , the covariance matrix of random effect, uses 4 parameters for autoregressive coefficients of
, the covariance matrix of random effect, uses 4 parameters for autoregressive coefficients of ![]() and
and![]() ,
, ![]() , (i and j index the dimension of b while
, (i and j index the dimension of b while ![]() means the
means the
![]() salamander’s latent effect) and plus 3 parameters for innovation variances of
salamander’s latent effect) and plus 3 parameters for innovation variances of![]() ,
, ![]() ,
,
![]() . Using this joint modelling method to analyze the real world data can estimate
. Using this joint modelling method to analyze the real world data can estimate ![]() more to the true one because of no factitious assumption on it, instead, only the data tells us what is
more to the true one because of no factitious assumption on it, instead, only the data tells us what is![]() . Another advantage is
. Another advantage is
the parameter is reduced from ![]() to 7 in
to 7 in![]() . This reduction of number of parameters makes the
. This reduction of number of parameters makes the
computation easier. Note that, the higher the dimension q, the more significant this advantage. Third, the modified Cholesky decomposition confirms that unconstrained parameters lead to strict condition that is the ![]() is a symmetric positive definite matrix.
is a symmetric positive definite matrix.
In the calculations, the convergence accuracy is set to be![]() . The
. The
numerical results from Tables 1-4 show that for each of the degree of freedom, QMC method make the maximum log-likelihood similar when increasing the number of QMC points from 10,000 to 100,000 which indicates any number of points between these could prove reasonable estimate of the parameters. In addition, the parameter estimates using these sequences become stable quickly. Bearing in mind that the integral space is
![]()
Table 1. MLEs of the parameters by covariance modelling for the pooled salamander data using square root sequence points when varying K, the number of square root sequence points (standard errors in parentheses) (random effect-multivariate![]() ).
).
![]()
Table 2. MLEs of the parameters by covariance modelling for the pooled salamander data using square root sequence points when varying K, the number of square root sequence points (standard errors in parentheses) (random effect-multivariate![]() ).
).
![]()
Table 3. MLEs of the parameters by covariance modelling for the pooled salamander data using square root sequence points when varying K, the number of square root sequence points (standard errors in parentheses) (random effect-multivariate![]() ).
).
![]()
Table 4. MLEs of the parameters by covariance modelling for the pooled salamander data using square root sequence points when varying K, the number of square root sequence points (standard errors in parentheses) (random effect-multivariate![]() ).
).
20-dimensional unit cube so that even if the number of the QMC points is chosen as![]() , it is still small in such a space. Nevertheless, the numerical results show that the QMC points approximation based estimation in the GLMMs performs very well in terms of accuracy and stabilization. When using 100,000 QMC points, our Fortran code takes about 50 minutes to obtain the results. Furthermore, the convergence of our algorithm is usually made between the 3th and 5th iterations. On the other hand, increasing the number of points may lead to less iterations.
, it is still small in such a space. Nevertheless, the numerical results show that the QMC points approximation based estimation in the GLMMs performs very well in terms of accuracy and stabilization. When using 100,000 QMC points, our Fortran code takes about 50 minutes to obtain the results. Furthermore, the convergence of our algorithm is usually made between the 3th and 5th iterations. On the other hand, increasing the number of points may lead to less iterations.
For mean model, the estimators for fixed effects, ![]() are similar when K increases over 30,000. For autoregressive coefficients (ACs) model, the estimations of
are similar when K increases over 30,000. For autoregressive coefficients (ACs) model, the estimations of![]() , including
, including![]() ,
, ![]() ,
, ![]() and
and ![]() are very close to zero. For logarithms of innovation variances (IVs), only
are very close to zero. For logarithms of innovation variances (IVs), only ![]() is not close to zero. It needs to be noted that some of standard deviations are 0.0000 for
is not close to zero. It needs to be noted that some of standard deviations are 0.0000 for ![]() and
and![]() , which means those values are less than
, which means those values are less than![]() .
.
A criteria easy to be executed to decide which covariate is significant is if the estimator is greater than twice of standard error. So the four fixed effect parameters of ![]() are significant; four parameters for
are significant; four parameters for ![]() are not;
are not; ![]() is significant, but
is significant, but ![]() and
and ![]() are not. The conclusion is that
are not. The conclusion is that![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() and
and ![]() can be regarded as zero. In other words, T is an identity matrix and D is a diagonal matrix with the same element. So
can be regarded as zero. In other words, T is an identity matrix and D is a diagonal matrix with the same element. So![]() , it can be said that every dimension of random effect of each salamander is independent of others. Also, the effects of female and male salamanders are independent and no heterogeneity between female and male.
, it can be said that every dimension of random effect of each salamander is independent of others. Also, the effects of female and male salamanders are independent and no heterogeneity between female and male.
Another point is why the random effect is not assumed as multivariate mixture normal distribution for the salamander data because Newton-Raphson algorithm does not achieve convergency until the mixture normal distribution degenerates to normal distribution.
6. Simulation
We conducted a simulation study to assess the efficiency of the QMC estimation in the GLMMs, in particular, to assess the performance of the GP set point when the distribution of random effect is multivariate t distribution (1) and multivariate mixture normal distribution (2). Based on the logistic model in (13), we simulate the sala- mander pooling data, which have 360 correlated binary observations. In the simulation study, we run 100 simulations. The same protocol design as the salamander mating experiment is adopted for the simulated data and the log-likelihood function for each simulated data set thus involves six 20-dimensional integrals that are analytically intractable.
When using the QMC approximation, we generate ![]() integration nodes on the cube
integration nodes on the cube ![]() using the square roots of the first 20 prime numbers (the GP set method). Then, we use Equation (6) to approximate the integrated log-likelihood when random effect followed multivariate t distribution. When random effect followed multivariate mixture normal distribution, the log-likelihood changes to
using the square roots of the first 20 prime numbers (the GP set method). Then, we use Equation (6) to approximate the integrated log-likelihood when random effect followed multivariate t distribution. When random effect followed multivariate mixture normal distribution, the log-likelihood changes to
![]() . (15)
. (15)
The Newton-Raphson algorithm (10) is used to maximize the approximated log-likelihood function. The true values are chosen to be (1.20, −2.80, −1.00, 3.60) for the fixed effects, ![]() for ACs para- meters and
for ACs para- meters and ![]() for IVs parameters. ACs parameters and IVs parameters build variance components. The starting values for the algorithm are chosen to be the estimators as for the real data analysis. The convergence criterion is set to be
for IVs parameters. ACs parameters and IVs parameters build variance components. The starting values for the algorithm are chosen to be the estimators as for the real data analysis. The convergence criterion is set to be ![]() for the successive iterated values. The algorithm stops after 20 iterations and is considered to be non-convergent. The simulation studies are conducted and coded in FORTRAN language and this programme was run on a PC Pentium (R) 4 PC (CPU 3.20 GHz). A summary of the simulation results is presented in Table 5 for multivariate t distribution and Table 6 for multivariate mixture normal distribution. The results given are the average parameter estimates based on 100 replications and their standard errors.
for the successive iterated values. The algorithm stops after 20 iterations and is considered to be non-convergent. The simulation studies are conducted and coded in FORTRAN language and this programme was run on a PC Pentium (R) 4 PC (CPU 3.20 GHz). A summary of the simulation results is presented in Table 5 for multivariate t distribution and Table 6 for multivariate mixture normal distribution. The results given are the average parameter estimates based on 100 replications and their standard errors.
It is clear that estimation by modified Cholesky decomposition with QMC approach is able to produce reasonably good results in GLMMs when the random effect is not normal distribution. When the random effects followed by multivariate t distribution (Table 5), the estimates of regression fixed effects and variance com- ponents are those on average of 100 simulation, which has little bias. That means the method of modified
Cholesky decomposition of covariance modelling with QMC approach is quite useful and effective. When the random effects followed by multivariate mixture normal distribution (Table 6), the estimates of regression fixed effects are acceptable although bigger bias, especially for fixed effects. The estimates of variance components are quite accurate. That is, when random effects change to two peaks distribution, the accuracy need to be en- hanced.
7. Conclusion and Discussion
It is quite common in the literatures that random effects are independent identically distributed normal variables in generalized linear models (GLMMs). In longitudinal study, the covariance-variance matrix of random effects for individuals is usually assumed to be homogeneous. However, this assumption may not be valid in practice. In this article, the assumption extends to random effects follow multivariate t and mixture normal distribution. Approximation of marginal quasi-likelihood and parameter estimation in GLMMs is very difficult and challenging because they involve integral on random effects, especially for high-dimensional problems.
In this article, we have used Quasi-Monte Carlo (QMC) sequence approximation to calculate the maximum likelihood estimates and marginal log quasi-likelihood in GLMMs. The key idea of QMC sequences is to generate integration points which are scatted uniformly in the integration domain. The good point, one simple QMC point, is used through this article. Newton-Raphson (NR) algorithm is the iterative method to obtain op- timum. QMC-NR method converges very quickly and performs very well in terms of accuracy and stabilization. In longitudinal studies, the covariance structure plays a crucial role in statistical inferences. The correct modelling of covariance structure improves the efficiencies of the mean parameters and provides much more reliable estimates (Ye and Pan, 2006, [16] ). The joint modelling (JM) for mean and for covariance-variance components for random effects reduces the number of parameters and has a clear statistical meaning. QMC-NR method with joint modelling can be called as QMC-NR-JM method. Although QMC-NR-JM method performs well in stability and produces accurate estimation of the parameters in GLMMs, there is no way to avoid intensive computation in real data analysis and simulation study. Particularly, the binary cross-designed sala- mander dataset, involving six 20-dimensional integrals in the log quasi-likelihood function, has been analyzed and the same protocol design is adopted for simulations.
Note that a practical issue is how to select of the number of integration points? My solution is increasing the number of QMC points gradually until the MLEs become stable. It correspondingly leads to increasing the computational time and efforts. This problem is quite obvious for simulation study, especially when the number of parameters increases. Another worth noting issue is that a range of starting values for the fixed effects and variance components have been tried and we find that the different starting values almost can’t change the results when algorithm reaches convergency.
In the QMC-NR-JM approximation method, the estimators of random effects cannot be calculated at the same time when estimating MLEs for fixed effects and variance components. Pan and Thompson (2007) [7] proposed an iterative method to predict of the random effects, implying that an initial value of b substituted into the equation to yield a new prediction of b. This process is then repeated until the convergence of![]() , but this method cannot guarantee convergence for arbitrary data. So how to estimate the random effects is still a open question in QMC-NR-JM method.
, but this method cannot guarantee convergence for arbitrary data. So how to estimate the random effects is still a open question in QMC-NR-JM method.
Acknowledgements
We thank the editors and the reviewers for their comments. This research is funded by the National Social Science Foundation No. 12CGL077, National Science Foundation granted No. 71201029, No.71303045 and No. 11561071. This support is greatly appreciated.
Appendix A. Second-Order Derivatives of Log-Likelihood Newton-Raphson Algorithm
![]()
where ![]() and
and ![]() are score function of log likelihood,
are score function of log likelihood, ![]() is Hessian matrix of log
is Hessian matrix of log
likelihood.
The second-order derivatives of log likelihood
![]()
![]()
![]()
![]()
Appendix B. MLEs for Covariance Modeling
The first and second derivative of ![]() respect to
respect to ![]() and
and ![]() are:
are:
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
![]() is introduced for the purpose of calculation for
is introduced for the purpose of calculation for![]() ,
, ![]() and
and![]() . Note that the
. Note that the
matrix ![]() looks similar to the matrix T, but opposite sign for the lower triangular elements.
looks similar to the matrix T, but opposite sign for the lower triangular elements.
![]() (19)
(19)
Every element in ![]() was rearranged into a response vector
was rearranged into a response vector![]() , such that
, such that![]() , i.e.,
, i.e.,
![]() (20)
(20)
We can put the ![]() column of
column of ![]() into a
into a ![]() lower triangular matrix like
lower triangular matrix like![]() . So we have
. So we have ![]()
![]() matrices. The element
matrices. The element ![]() in (20) can be put into the place
in (20) can be put into the place ![]() in the
in the ![]() matrix. For the
matrix. For the ![]() matrix,
matrix, ![]() , we have the relationship
, we have the relationship ![]() where
where![]() ,
, ![]() and
and
![]() .
.
The above relationship is a one-to-one correspondence between i and![]() . So
. So ![]() and
and ![]() in (20) can be also expressed as
in (20) can be also expressed as
![]() (21)
(21)
![]() is a lower triangular matrix with 1’s as diagonal entries, so that
is a lower triangular matrix with 1’s as diagonal entries, so that![]() ,
, ![]() and
and ![]()
are all lower triangular matrices. Denote ![]() where
where
![]() (22)
(22)
The first derivative can be calculated as
![]() (23)
(23)
where ![]() is a lower triangular matrix with 0’s as diagonal entries and
is a lower triangular matrix with 0’s as diagonal entries and ![]() as the entries below diagonal.
as the entries below diagonal.
The second derivative can be calculated as
![]() (24)
(24)
![]() (25)
(25)
because of![]() ,
,![]() . We also have
. We also have
![]() (26)
(26)
![]() (27)
(27)
![]() (28)
(28)
where
![]() (29)
(29)
![]() (30)
(30)
![]() (31)
(31)
![]() (32)
(32)
NOTES
*Corresponding author.