Spectral Gradient Algorithm Based on the Generalized Fiser-Burmeister Function for Sparse Solutions of LCPS ()
1. Introduction
Given a matrix 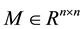 and an n-dimensional vector q, the linear complementarity problem, denoted by LCP(q, M), is to find a vector
and an n-dimensional vector q, the linear complementarity problem, denoted by LCP(q, M), is to find a vector 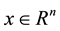 such that
such that
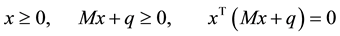 .
.
The set of solutions to this problem is denoted by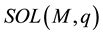 . Throughout the paper, we always suppose
. Throughout the paper, we always suppose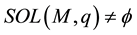 . The LCP has many wide applications in physics, engineering, mechanics, and economics design [1] [2] . Numerical methods for solving LCPs, such as the Newton method, the interior point method and the non-smooth equation methods, have been extensively investigated in the literature. However, it seems that there are few methods to solve the sparse solutions for LCPs. In fact, it is very necessary to research the sparse solution of the LCPs such as portfolio selection [3] [4] and bimatrix games [5] in real applications.
. The LCP has many wide applications in physics, engineering, mechanics, and economics design [1] [2] . Numerical methods for solving LCPs, such as the Newton method, the interior point method and the non-smooth equation methods, have been extensively investigated in the literature. However, it seems that there are few methods to solve the sparse solutions for LCPs. In fact, it is very necessary to research the sparse solution of the LCPs such as portfolio selection [3] [4] and bimatrix games [5] in real applications.
In this paper, we consider the sparse solutions of the LCP. We call 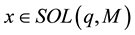 a sparse solution of LCP (q, M) if
a sparse solution of LCP (q, M) if 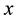 is a solution of the following optimization problem
is a solution of the following optimization problem
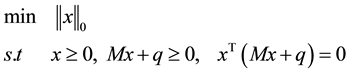 (1)
(1)
To be more precise, we seek a vector  by solving the l0 norm minimization problem, where
by solving the l0 norm minimization problem, where 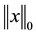 stands for the number of nonzero components of x. A solution of (1) is called the sparsest solution of the LCP.
stands for the number of nonzero components of x. A solution of (1) is called the sparsest solution of the LCP.
Recently, Meijuan Shang, Chao Zhang and Naihua Xiu design a sequential smoothing gradient method to solve the sparse solution of LCP [6] . We inspire by the model and use the spectral method based on the generalized Fischer-Burmeister function to solve our new model (3). The spectral method is proposed by Barzilai and Borwein [7] and further analyzed by Raydan [8] [9] . The advantage of this method is that it requires little computational work and greatly speeds up the convergence of gradient methods. Therefore, this technique has received successful applications in unconstrained and constrained optimizations [10] -[13] .
In fact, the above minimization problem (1) is a sparse optimization with equilibrium constraints. From the problem of constraint conditions, as well as the non-smooth objective function, it is difficult to get solutions due to the equilibrium constraints to overcome the difficultly, and we use the NCP-functions to construct the penalty of violating the equilibrium constraints.
A function φ: R2 → R1 is called a NCP-function, if for any pair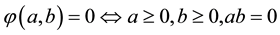
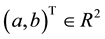 .
.
A popular NCP-functions is the Fischer-Burmeister (FB), which is defined as
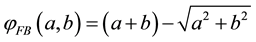
The Fischer-Burmeister function has many interesting properties. However, it has limitations in dealing with monotone complementarity problems since it is too flat in the positive orthant, the region of main interest for a complementarity problem. In terms of the above disadvantage of the Fischer-Burmeister function, we consider the following generalized Fischer-Burmeister function [10] .
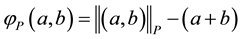 (2)
(2)
where p is any fixed real number from 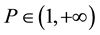 and
and 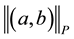 denotes the p-norm, i.e.
denotes the p-norm, i.e.
![]()
In other words, in the function![]() , we replace the 2-norm of
, we replace the 2-norm of ![]() in the FB function
in the FB function ![]() by a more general p-norm of
by a more general p-norm of![]() . The function
. The function ![]() is still an NCP-function.
is still an NCP-function.
Define ![]() by
by
![]()
where ![]() with
with ![]() and
and![]() . Obviously,
. Obviously, ![]() if and only if
if and only if![]() . By further employing the lp regularization term for seeking sparsity, we obtain the following unconstrained minimization problem to approximate
. By further employing the lp regularization term for seeking sparsity, we obtain the following unconstrained minimization problem to approximate
![]() (3)
(3)
where ![]() is a given regularization parameter, and
is a given regularization parameter, and ![]() for any 0 < p < 1. We call (3) as lp
for any 0 < p < 1. We call (3) as lp
regularized minimization problem.
Let us denote the first term of (3) by the function![]() . That is
. That is
![]() (4)
(4)
For any given![]() , the function
, the function ![]() is shown to possess all favorable properties of the FB function; we can see [8] . It plays an important part in our study throughout the paper. We observe in [14] [15] that P has a great influence on the numerical performance of certain descent-type methods; a larger P yields a better convergence rate, whereas a small P often gives a better global convergence.
is shown to possess all favorable properties of the FB function; we can see [8] . It plays an important part in our study throughout the paper. We observe in [14] [15] that P has a great influence on the numerical performance of certain descent-type methods; a larger P yields a better convergence rate, whereas a small P often gives a better global convergence.
The paper is organized as follows: In Section 2, we present absolute lower bounds for nonzero entries in local solution of (3). In section 3, we approximate the minimal zero norm solutions of the LCP. In section 4, we give a sequential smoothing spectral gradient method to solve the model. In Section 5, numerical results are given to demonstrate the effectiveness of the sequential smoothing spectral gradient method.
2. The lp Regularized Approximation
In this section, we consider the minimizers of (3). We study the relation between the original model (1) and the lp regularized model (3), which indicates the regularized model is a good approximation. We use a threshold lower bound L [6] for nonzero entries in local minimizers and the choice of the lp minimization problem (3).
2.1. Relation between (3) and (1)
The following result is given in [6] , which is essentially based on some results given by Chen Xiaojun [14] .
Lemma 2.1. [6] for any fixed ![]() the solution set of (3) is nonempty and bounded. Let
the solution set of (3) is nonempty and bounded. Let ![]() be a solution
be a solution
of (3), and ![]() be any positive sequence converging to 0. If
be any positive sequence converging to 0. If![]() , then
, then ![]() has at least one accumulation point, and any accumulation point
has at least one accumulation point, and any accumulation point ![]() of
of ![]() is a solution of (3). That is, for any
is a solution of (3). That is, for any ![]() satisfied
satisfied
![]() and
and![]() .
.
2.2. Lower Bounds for Nonzero Entries in Solutions
In this section, we extend the above result to the lp norm regularization model (2) for approximating minimal l0 norm solutions of the LCP. We provide a threshold lower bound L > 0 for any local minimizer, and show
that any nonzero entries of local minimizers must exceed L. Since![]() , the objective function
, the objective function ![]()
is bound below and ![]() if
if![]() . Moreover, the set
. Moreover, the set ![]() of local minimizers of (3) is nonempty and bounded.
of local minimizers of (3) is nonempty and bounded.
Lemma 2.2. [6] let ![]() be any local minimizer of (3) satisfying
be any local minimizer of (3) satisfying ![]() for an arbitrarily given point
for an arbitrarily given point![]() . Set
. Set
![]() (5)
(5)
Then we have: for any![]() .
.
Moreover, the number of nonzero entries in ![]() is bounded.
is bounded.
![]()
Let us denote the first term of (3) by the function![]() . That is
. That is
![]() (6)
(6)
First we present some properties of ![]() and
and![]() .
.
Lemma 2.3. [12] let ![]() be given by (3). Then, the following properties hold:
be given by (3). Then, the following properties hold:
1) ![]() is a positive homogeneous and sub-additive NCP-function.
is a positive homogeneous and sub-additive NCP-function.
2) ![]() is strongly semismooth.
is strongly semismooth.
3) If ![]() with
with![]() , or
, or![]() , or
, or![]() ,
, ![]() , then
, then ![]()
when![]() .
.
4) Given a point![]() , very element in the generalized gradient
, very element in the generalized gradient ![]() has the representation
has the representation![]() , where
, where
![]() and for
and for
sgn(.) represents the sign function; ![]() and
and ![]() are real numbers that satisfy
are real numbers that satisfy![]() .
.
Theorem 2.1. The function ![]() is continuously differentiable everywhere and the gradient of
is continuously differentiable everywhere and the gradient of ![]() can be obtained by
can be obtained by
![]() (7)
(7)
where ![]() and
and ![]() are diagonal matrices whose diagonal element is giv-
are diagonal matrices whose diagonal element is giv-
en by
![]()
![]()
where ![]() is any vector satisfying
is any vector satisfying![]() .
.
3. Smoothing Method for lp Regularization
Most optimization algorithms are efficient only for convex and smooth problems. However, some algorithms for
Non-smooth and non-convex optimization problems have been developed recently. Note that the term ![]() (0 <
(0 <
p < 1) in (3) is neither convex nor Lipschitz continuous in![]() . Solving the non-convex, non-Lipschitz continuous minimization problem is not easy. We use some approximation methods to surmount the non-Lipschitz continuity problem in solving (3).
. Solving the non-convex, non-Lipschitz continuous minimization problem is not easy. We use some approximation methods to surmount the non-Lipschitz continuity problem in solving (3).
Smoothing Counterpart for (3)
For![]() , let
, let
![]() (8)
(8)
It is clear to see that, for any![]() ,
,
![]()
and ![]() is continuously differentiable with
is continuously differentiable with
![]()
We can construct a smoothing approximation of (2) as
![]() (9)
(9)
by noting that ![]() is continuously differentiable, and
is continuously differentiable, and ![]() since
since
![]() (10)
(10)
for any![]() .
.
Let ![]() denote the set of local minimizers of (10). We have the similar results as in Lemmma 2.1 and 2.2, corresponding to the smoothing counterpart (10).
denote the set of local minimizers of (10). We have the similar results as in Lemmma 2.1 and 2.2, corresponding to the smoothing counterpart (10).
Theorem 3.1. Let ![]() be a sequence of vectors being global minimizers of (10) with
be a sequence of vectors being global minimizers of (10) with ![]() as
as![]() .
.
Then, any accumulation point of ![]() is a global minimizer of (3).
is a global minimizer of (3).
Proof. Let ![]() be a global minimizer of (3) and
be a global minimizer of (3) and ![]() be an accumulation point of
be an accumulation point of![]() .
.
We can deduce from (11) that
![]()
On the other hand, we have![]() , and consequently
, and consequently
![]()
Which indicates ![]() is a global minimizer of (3).
is a global minimizer of (3).
Lemma 3.2. [6] for any![]() , let
, let ![]() be any local minimizer of (14) satisfying
be any local minimizer of (14) satisfying ![]() for an arbitrarily given initial points
for an arbitrarily given initial points![]() . Let L be defined in Lemma 2.2. Then, we have for any
. Let L be defined in Lemma 2.2. Then, we have for any
![]()
4. SS-SG Algorithm
We suggest a sequential Smoothing Spectral Gradient (SS-SG) Method to solve (3). With the SS-SG method, we need the Spectral Gradient method as the main step for decreasing the objective value. The smoothing method is very easy to implement and efficient to deal with optimization; see [15] .
We first introduce the spectral projected gradient method in [8] as follow.
Algorithm 1. Smoothing Spectral Gradient Method
Step 0: Choose an initial point![]() , and parameters
, and parameters![]() ,
, ![]() ,
,![]() . Let
. Let![]() ,
, ![]() ,
,![]() .
.
Step1: Let![]() ,
, ![]() ,
, ![]() where
where![]() ,
,![]() . If
. If
![]() , then stop.
, then stop.
Step 2: Compute the step size ![]() by the Armijo line search, where
by the Armijo line search, where ![]() satisfies
satisfies
![]()
Set![]() .
.
Step 3: If![]() , then set
, then set![]() ; otherwise, choose
; otherwise, choose![]() .
.
Algorithm 2. Sequential Smoothing Spectral Gradient Method
Step 1: Find ![]() by using the algorithm 1 to solve
by using the algorithm 1 to solve
![]()
Step 2: Compute
![]()
Use the lower bound ![]() to set the entries of
to set the entries of ![]() with small values to zeros and obtain the computed solution
with small values to zeros and obtain the computed solution ![]() with
with
![]()
Step 3: Decrease the parameter ![]() and set
and set![]() .
.
5. Numerical Experiments
In this section, we test some numerical experiments to demonstrate the effectiveness of our SG algorithm. In order to illustrating the effectiveness of the SS-SG algorithm we proposed, we introduce another algorithm of talking the LCPs. In [6] , the authors designed a sequential smoothing (SSG) method to solve the lp regularized model and get a sparse solution of LCP(q, M). Numerical experiments show that our algorithm is more effective than (SSG) algorithm.
The program code was written in and run in MATLAB R2013 an environment. The parameters are chooses as![]() ,
, ![]() and
and![]() . The maximum number of iterations in step 1 is set to be 2000. We end the SS-SG algorithm in Step 1, if
. The maximum number of iterations in step 1 is set to be 2000. We end the SS-SG algorithm in Step 1, if ![]() and
and![]() , or it reaches the maximum number of iterations.
, or it reaches the maximum number of iterations.
5.1. Test for LCPs with Positive Semidefinite Matrices
Example 1. We consider the LCP(q, M) with
![]()
The solution set is![]() .
.
When![]() , the vector
, the vector ![]() is the sparse solution of LCP(q, M). We choose P = 10, p = 0.1 in (3) for this small example, and use our SS-SG algorithm with the regularization parameter
is the sparse solution of LCP(q, M). We choose P = 10, p = 0.1 in (3) for this small example, and use our SS-SG algorithm with the regularization parameter![]() . We use the initial point
. We use the initial point![]() , we get a minimal
, we get a minimal ![]() norm solution
norm solution ![]() and the distance
and the distance
![]() .
.
Example 2. We consider the LCP(q, M) with
![]()
The solution set is
![]()
When![]() , the vector
, the vector ![]() is the sparse solution of LCP(q, M). When
is the sparse solution of LCP(q, M). When![]() , the vector
, the vector
![]() is the sparse solution of LCP(q, M). We choose the same parameters as Example 1. We use the initial point
is the sparse solution of LCP(q, M). We choose the same parameters as Example 1. We use the initial point![]() , we get a minimal
, we get a minimal ![]() norm solution
norm solution ![]() and the distance
and the distance
![]() . We use the initial point
. We use the initial point![]() , we get a minimal
, we get a minimal ![]() norm solution
norm solution ![]() and the distance
and the distance![]() .
.
These examples show that, given the proper initial point, our algorithm can effectively find an approximate sparse solution.
5.2. Test for LCPs with Z-Matrix [6]
Let us consider LCP(q, M) where
![]() and
and![]()
Here ![]() is the identity matrix of order n and
is the identity matrix of order n and![]() . Such a matrix M is widely used in statistics. It is clear that Mis a positive semidefinite Z-matrix. For any scalar
. Such a matrix M is widely used in statistics. It is clear that Mis a positive semidefinite Z-matrix. For any scalar![]() , we know that the vector
, we know that the vector ![]() is a solution to LCP(q, M), since it satisfies that
is a solution to LCP(q, M), since it satisfies that
![]()
Among all the solutions, the vector ![]() is the unique sparsest solution. We test the SS-SG algorithm for different dimensions with n = 100, 300, 500, 1000, 1300, respectively. In this set of experiments, we set
is the unique sparsest solution. We test the SS-SG algorithm for different dimensions with n = 100, 300, 500, 1000, 1300, respectively. In this set of experiments, we set![]() .The results are displayed in Table 1.
.The results are displayed in Table 1.
In Table 1, “![]() ” denotes the Euclidean distance between
” denotes the Euclidean distance between ![]() and the true sparsest
and the true sparsest![]() , and “time” denotes the computational time in seconds. Form Table 1, we can see that the SS-SG algorithm is effective to find the sparse solution of LCPs.
, and “time” denotes the computational time in seconds. Form Table 1, we can see that the SS-SG algorithm is effective to find the sparse solution of LCPs.
In order to test the effectiveness of the SS-SG algorithm, we compare with the SSG algorithm of talking the LCPs. In [10] , the authors use the Fiser-Burmeister function established a lp (0 < p < 1) regularized minimization model and designed a SSG method to solve the LCPs. The results are displayed in Table 2, where “_” denotes the method is invalid. Although the sparsity ![]() is same and the recovered errors
is same and the recovered errors ![]() are pretty small, the average cpu time less than the SSG algorithm.
are pretty small, the average cpu time less than the SSG algorithm.
![]()
Table 1. SS-SG’s computation results on LCPs with Z-matrices.
![]()
Table 2. SSG’s computation results on LCPs with Z-matrices.
6. Conclusion
In this paper, we have studied a lp (0 < p < 1) model based on the generalized FB function defined as in (2) to find the sparsest solution of LCPs. Then, an lp normregularized and unconstrained minimization model is proposed for relaxation, and we use a sequential smoothing spectral gradient method to solve the model. Numerical results demonstrate that the method can efficiently solve this regularized model and gets a sparsest solution of LCP with high quality.
Acknowledgements
This work is supported by Innovation Programming of Shanghai Municipal Education Commission (No. 14YZ094).