A Real-Time Transient Analysis of a Functionally Graded Material Plate Using Reduced-Basis Methods ()
1. Introduction
Generally, a complex structure is modeled by a discrete multi-degree-of-freedom system, and the dynamic analysis of them often requires solving a large set of equations. Nevertheless the numerically solution of the transient structural response for such a large system is expensive; thus methods that can not only reduce significantly the size of the problem and the computational cost but also retain the accuracy of the solution and the physics of the structures are very desirable.
Many methods on model-order reduction, such as Guyan reduction [1] , Ritz vectors reduction [2] , proper orthogonal decomposition [3] , balanced truncation [4] , and various related hybrid techniques [5] [6] , have been developed to reduce the problem size of structures. Recently, there has been considerable interest in the reduced-basis method (RBM) [7] - [10] , a very promising numerical method, which requires a projection onto the reduced-basis space constructed by the solutions of the interest sample parameter points, which is very suitable for the analysis of large system. The RBM has first been introduced in the late 1970s for single-parameter problems in nonlinear structural analysis and subsequently developed for multi-parameter problems. However, RBM has rarely been extended to the real-time analysis of the dynamic problems yet, especially the transient analysis of large complex structures.
Hybrid numerical method (HNM) which combines the finite element method with the Fourier transform, a very efficient method to perform the transient analysis of laminated structures, is proposed by Liu et al [11] . Later the modified HNM [12] [13] is developed to analyze the associated characteristics of functionally graded material (FGM) structures. In the modified HNM, the structures are firstly divided into inhomogeneous layered elements in one direction. A set of partial differential equations (PDEs) is developed to approximate the dynamic equilibrium of the FGM structures by applying the principle of virtual work and assembling the matrices of adjacent elements. The PDEs are solved effectively through a space-wavenumber Fourier transform. However, the repeated calculations of eigenvalue problems in wavenumber domain are very expensive, especially in the three-dimensional case where structures are subjected to a point load.
In this paper we apply the reduced-basis method in wavenumber domain to the transient analysis of structures based on the modified HNM. The truncated eigenvectors corresponding to the carefully selected sample parameter points are extracted to construct the reduced-basis space onto which the original large system problem is projected. In this manner, a reduced system is obtained and the eigenvalue problem can be solved more effectively. And then the eigenvectors of the full problem are obtained by the inverse projection; the response in wavenumber domain can be obtained by a real-time manner. Eventually the transient response in space-time domain is obtained through performing the inverse Fourier transform.
2. Brief Introduction of the Modified HNM to FGM Plate
A functionally graded material (FGM) plate with varying material properties in the thickness direction as shown in Figure 1 is considered. The plate is composed of two materials and divided into N layered element in the thickness direction. Without losing the generality, the elastic modulus matrix of an element possesses 21 different constants. H is the thickness of the plate and 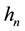 is the thickness of the nth element. The displacement field, elastic constants and mass density of the nth element are approximated as [13] :
is the thickness of the nth element. The displacement field, elastic constants and mass density of the nth element are approximated as [13] :
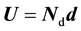 (1)
(1)
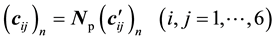 (2)
(2)
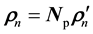 (3)
(3)
where 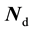 and
and 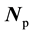 are the shape function matrices of the second-order interpolations. d denotes the nodal displacement vector, which are functions of x, y and time t, at
are the shape function matrices of the second-order interpolations. d denotes the nodal displacement vector, which are functions of x, y and time t, at ,
, 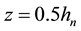 and
and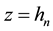 , as following:
, as following:
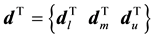 (4)
(4)
where
 (5)
(5)
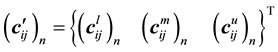 , (6)
, (6)
The superscripts l, m and u denote the lower, middle and upper surfaces of the nth element respectively.
The initial conditions of the plate are given by:
![]()
Figure 1. A functionally graded material plate and the nth isolated layered element.
 (7)
(7)
d is the transient displacement responses vector of the nodal planes and “.” denotes the differentiation with respect to time t.
With the principle of virtual work, a set of approximate partial differential equations for an element is obtained. The dynamic equilibrium equation of the whole plate can be formed by assembling the matrices of all the adjacent elements. The Fourier transform from space to wavenumber is used to deduce a set of system equations of the FGM plate in wavenumber domain [13] .
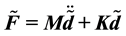 (8)
(8)
where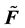 ,
, ![]() , and
, and ![]() are the Fourier transform of load, acceleration, and displacement, respectively. Hermitian stiffness matrix
are the Fourier transform of load, acceleration, and displacement, respectively. Hermitian stiffness matrix ![]() is given by
is given by
![]() (9)
(9)
which is constant matrix for the given wavenumbers kx and ky. The expressions of the matrices ![]() and mass matrix
and mass matrix ![]() can refer to [13] . The dimension of the stiffness and mass matrices is
can refer to [13] . The dimension of the stiffness and mass matrices is
![]()
3. The Introduce of RBM into the Modified HNM
An alternative expression of Equation (8) can be obtained through rearranging columns and rows in the matrices by degrees of freedom rather than by interface. The resulting representation is given by
![]() (10)
(10)
where![]() ,
, ![]() ,
, ![]() (i = 1, 2, 3, 6).
(i = 1, 2, 3, 6).![]() ,
, ![]() ,
, ![]() (j = 4, 5).
(j = 4, 5).
In the particular case where the elastic material possesses a symmetric plane, multiplying the third row of Equation (10) by ![]() and factoring out i from the third column, the stiffness matrix
and factoring out i from the third column, the stiffness matrix ![]() can be turned to a real symmetrical one and expressed as follows.
can be turned to a real symmetrical one and expressed as follows.
![]() (11)
(11)
where ![]() includes the two parameters
includes the two parameters![]() . The displacement
. The displacement ![]() can be evaluated through the modal superposition using the conjugated eigenvectors of the generalized eigenvalue equation:
can be evaluated through the modal superposition using the conjugated eigenvectors of the generalized eigenvalue equation:
![]() (12)
(12)
The above equation can be converted to standard form by performing Cholesky decomposition of mass matrix.![]() .
.
![]() (13)
(13)
where ![]() is the characteristic matrix.
is the characteristic matrix.
![]() , (14)
, (14)
It requires the repeated analysis of eigenvalue problem in wavenumber domain. When the inverse Fourier transform is performed, the range of integration is theoretically from negative infinite to positive infinite wavenumbers. For a practical calculation, the ranges of wavenumbers and the number of sampling points should be chosen properly according to the required accuracy before Fourier transform. Generally, hundreds of sample points in wavenumber domain are required to guarantee the accuracy of results. Nevertheless, the eigenvalue problem for individual wavenumber should be solved to perform the modal superposition before the inverse Fourier transform, this is computationally expensive. Furthermore, for higher accuracy of results, the computational cost will increase exponentially when layered element is adopted.
The expensive computational cost of the repeated analysis for the large eigenvalue problems can be decreased by reduced-basis method through an off-line/on-line decomposition [14] [15] . Figure 2 provides the procedure of the real-time analysis of the transient response.
At off-line stage, we introduce a sample set ![]() in the wavenumber domain, assuming G can be exactly divided by m. m denotes the number of truncated eigenvectors from Equation (13) associated with the desired accuracy of calculation. The sample points are logarithmically distributed in the sense that [15] :
in the wavenumber domain, assuming G can be exactly divided by m. m denotes the number of truncated eigenvectors from Equation (13) associated with the desired accuracy of calculation. The sample points are logarithmically distributed in the sense that [15] :
![]() (15)
(15)
where G is the number of the sample point, ![]() denotes the maximum wavenumber,
denotes the maximum wavenumber, ![]() is a constant to guarantee the relationship between the serial number of the sample points and the value of the corresponding wavenumber. Figure 3 gives the logarithmically distribution of the sample points. For each input in
is a constant to guarantee the relationship between the serial number of the sample points and the value of the corresponding wavenumber. Figure 3 gives the logarithmically distribution of the sample points. For each input in![]() , we solve the standard eigenvalue problem Equation (13).
, we solve the standard eigenvalue problem Equation (13).
A reduced-basis space can be introduced by extracting the first m eigenvectors of each point in the sample set as follows [8] :
![]() (16)
(16)
To simplify the notation, we rewrite Equation (16) as follows:
![]() (17)
(17)
The bases of above equation are orthonormalized to guarantee their independence, and then the approximate eigenvectors of the standard eigenvalue problem for a new ![]() can be expressed as follows through a standard
can be expressed as follows through a standard
![]()
Figure 2. Off-line/on-line decomposition procedure of transient analysis.
![]()
Figure 3. The logarithmic distribution of sample points in wavenumber domain for piecewise approximation.
Galerkin projection:
![]() (18)
(18)
where the subscript j denotes the jth mode, ‘^’ denotes the approximated variable. It can also be rewritten in the form of a matrix.
![]() (19)
(19)
where ![]() is a
is a ![]() matrix, and
matrix, and ![]() is the generalized coordinates column.
is the generalized coordinates column.
The matrices independent of wavenumber are projected onto the reduced-basis space:
![]() (20)
(20)
At on-line stage, because of the wavenumber independence of![]() , we can form the reduced-basis characteristic matrix and explore the whole wavenumber domain easily.
, we can form the reduced-basis characteristic matrix and explore the whole wavenumber domain easily.
![]() (21)
(21)
The resultant reduced eigenvalue problem can be expressed as:
![]() (22)
(22)
where![]() . The truncated eigenvectors of the original large system for arbitrary
. The truncated eigenvectors of the original large system for arbitrary ![]() can be regenerated using the following equation.
can be regenerated using the following equation.
![]() (23)
(23)
Combining the method of modal analysis, the initial condition Equation (7) with the addition of the Duhamel integral, the displacements in Fourier transform domain can be obtained.
Finally, the approximate displacement response in the space-time domain can be obtained by performing the inverse Fourier transform.
It is considerable for the reduced standard eigenvalue problem that the reduced-basis space which is constructed by the truncated modes can only approximate the same modes of the eigenvalue problem for a new![]() . The size of the reduced system equation is independent of the original system, it depends on the required accuracy and the selected sample set.
. The size of the reduced system equation is independent of the original system, it depends on the required accuracy and the selected sample set.
4. The Error Bound of Approximated Eigen-Pairs
According to the classical theory of matrix projection, the following equation holds if Z is an invariant subspace for matrix Q.
![]()
Here ![]() is an orthogonal projection matrix. However, an error will be introduced for an approximated subspace.
is an orthogonal projection matrix. However, an error will be introduced for an approximated subspace.
![]()
![]() denotes the deviation matrix of the approximated subspace within invariant subspace, which can be expressed as:
denotes the deviation matrix of the approximated subspace within invariant subspace, which can be expressed as:
![]()
The Euclid Norm is defined as:
![]()
It is easy to guarantee the error within bound of eigenvalue.
![]()
The error of eigenvectors is also bounded.
5. Results and Discussions
The present method is applied to an actual stainless steel-silicon nitride (SS-SN) FGM plate, in which the silicon nitride is considered as the inclusion material. The material constants for SS-SN are listed in Table 1 [16] . The volume fraction of SN is assumed as the following simple power law distribution in the thickness direction:
![]() (24)
(24)
The material property of the FGM can be obtained by using the rule-of-mixture [16] . The whole plate is divided into 10 layered elements and has 63 degrees of freedom.
In the computational procedure, the following dimensionless parameters are used [13] .
![]() (25)
(25)
For the SS-SN FGM plate, the SS material is taken as the referenced material, ![]() ,
, ![]() ,
, ![]() and
and ![]() are the mass density, the shear modulus, the velocity of shear wave in SS material and the time for the shear wave to cross the plate thickness, respectively.
are the mass density, the shear modulus, the velocity of shear wave in SS material and the time for the shear wave to cross the plate thickness, respectively.
Consider two-dimensional case, a vertical line sin load is acted on the upper surface at![]() :
:
![]() (26)
(26)
where
![]() (27)
(27)
![]() (28)
(28)
Equation (26) implies that the time history of the load is only one cycle of the sin function, ![]() is a constant amplitude vector and
is a constant amplitude vector and ![]() is a constant. The observation position is at
is a constant. The observation position is at ![]() on the upper surface of the plate.
on the upper surface of the plate.
In this case where ![]() and
and ![]() should only be taken into account. The range of wavenumber [0, 64p] is divided into 751 points, the sub domains are cut by some prescribed sample points. Due to the well behavior of dispersion in wavenumber domain, we adopt a piecewise approximation. And the eigenvectors are only from two external points used to construct the reduced-basis space in each sub domain. In the two-dimensional transient analysis of structures, the first six eigenvectors are only needed to perform the modal superposition. The reason is that it needs only the first several natural modes to perform the modal superposition in practice, while the effect of the high order modes on the result is little. Therefore, the truncated eigenvectors from the two sample points are extracted to construct a reduced-basis space of 12 basis vectors in each sub domain. The original large eigenvalue problem can be reduced to
should only be taken into account. The range of wavenumber [0, 64p] is divided into 751 points, the sub domains are cut by some prescribed sample points. Due to the well behavior of dispersion in wavenumber domain, we adopt a piecewise approximation. And the eigenvectors are only from two external points used to construct the reduced-basis space in each sub domain. In the two-dimensional transient analysis of structures, the first six eigenvectors are only needed to perform the modal superposition. The reason is that it needs only the first several natural modes to perform the modal superposition in practice, while the effect of the high order modes on the result is little. Therefore, the truncated eigenvectors from the two sample points are extracted to construct a reduced-basis space of 12 basis vectors in each sub domain. The original large eigenvalue problem can be reduced to ![]() by projection.
by projection.
![]()
Table 1. Material constants of stainless steel and silicon nitride monolith [13] .
The eigen-pairs analysis in six wavenumbers, namely![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() are applied to validate the present reduced-basis method when 15 sample points are selected. As comparison, the error of eigenvalues is listed in Table 2, and the norm error of eigenvectors is listed in Table 3. The biggest error of eigenvalues from RBM is 0.69706%, and RBM almost exactly regenerates the eigen-pairs in the second and the forth mode. The other eigen-pairs from RBM are also agreement with that from HNM without the introducing of RBM very well. The RBM simulation can obtain the sufficient accuracy for the practical engineering and the high reliability for the numerical calculation.
are applied to validate the present reduced-basis method when 15 sample points are selected. As comparison, the error of eigenvalues is listed in Table 2, and the norm error of eigenvectors is listed in Table 3. The biggest error of eigenvalues from RBM is 0.69706%, and RBM almost exactly regenerates the eigen-pairs in the second and the forth mode. The other eigen-pairs from RBM are also agreement with that from HNM without the introducing of RBM very well. The RBM simulation can obtain the sufficient accuracy for the practical engineering and the high reliability for the numerical calculation.
![]()
Table 2. The error of the first six eigenvalues from RBM with respect to that without RBM at six wavenumbers (%).
![]()
Table 3. The error norm of the first six eigenvectors from RBM with respect to that without RBM at six wavenumbers (%).
Either too many or too few sample points selected in the parameter domain is unfeasible, the former leads to computational inefficiency, while the latter leads to unacceptable error. There is often a tradeoff between the computational cost and the accuracy of the simulated result. The transient displacements from RBM with 6, 8 and 15 sample points compared with that from HNM without the introducing of RBM are drawn in Figure 4 and Figure 5 respectively. It can be seen from Figure 4 that the simulated result will be distorted if too few points of the sample set is selected, especially in the duration when loads are unloaded. Figure 5 shows that the results from RBM are agreement with that from HNM without using RBM very well. Fortunately, it can be found that the results from RBM become steady when the number of the sample points increases up to a critical number 8, as let us avoid dealing with the tradeoff.
![]()
Figure 4. Comparison of the response of time history on the upper surface (with 6 sample points or without RBM).
![]()
Figure 5. Comparison of the response of time history on the upper surface (with 8, 15 sample points or without RBM).
![]()
Table 4. Computational costs for the analysis of eigenvalue problems with or without the introduce of RBM.
The Fortran codes for the calculation of transient displacements are executed on a PC with a CPU clock speed of 2.8 GHz. The CPU time for the analysis of eigenvalue problems with and without the introducing of RBM are compared in Table 4 and it can be found that time of the former is about 38.8% of the later. It is mainly reason that the efficient off-line/on-line decomposition is used. In addition, the projection of the original eigenvalue problem onto the reduced-basis spaces is just a procedure to perform multiplication of several matrices, as costs very little CPU time. The efficiency can be further enhanced when the layered element refined for higher accuracy. For a practical dynamic analysis of complex structures, the number of degree-of-freedom is typically extremely large, and in particular much too large to perform transient response analysis. Fortunately, the size of the system equations projected onto the reduced-basis space is independent of the original system rather decided by the dimensions of the reduced-basis space. No matter how large the system structure is, it always can be reduced to a small size by reduced-basis method while the physics of the original structures are retained, as ensure us to perform the accurate transient response analysis by a real-time manner.
6. Conclusion
A reduced-basis method in wavenumber domain is proposed to obtain the real-time transient response of FGM plate based on the modified HNM in this paper. The repeated and expensive numerical analyzes of the large eigenvalue problems have been simplified by RBM. Through a real-time off-line/on-line decomposition technique, high accuracy and less cost of the simulation are achieved. Because of the outstanding performance of the RBM, it is a promising numerical method which can be extended to the dynamic analysis of other complex structures.
Acknowledgements
This project is supported by National Natural Science Foundation of China (Grant No. 51305045), and by China Postdoctoral Science Foundation (No. 2014M562099).