On the Power Performance of Test Statistics for the Generalized Rayleigh Interval Grouped Data ()
1. Introduction
In many real practical applications, when it is not feasible to have a complete data for statistical inference about the hypothesized statistical model, grouped data arise frequently in many fields of economics, medicine, engineering and variety branches of science. In survival and reliability analysis, performing industrial life testing experiments by continuous monitoring the test units may incorporate an error measurements in some failure units, tediously, costly and time consuming in many situations. Therefore, it is more convenient to inspect the test units intermittently for failure by initially dividing the time scale line into adjacent intervals by constant inspection times 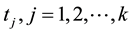 to have the interval grouped which mainly consists of the numbers of failure units in the given intervals. Having the interval grouped data from the continuous lifetime model may override the testing settings but increases the efforts needed for making any statistical inference. Such type of data is considered by many authors as in Pipper and Ritz [1] , Aludaat [2] and Migdadi and Al-Batah [3] .
to have the interval grouped which mainly consists of the numbers of failure units in the given intervals. Having the interval grouped data from the continuous lifetime model may override the testing settings but increases the efforts needed for making any statistical inference. Such type of data is considered by many authors as in Pipper and Ritz [1] , Aludaat [2] and Migdadi and Al-Batah [3] .
Many researchers have proposed and modified test statistics for fitting grouped data to the hypothesized statistical distributions. Initially, the Chi Square test statistic proposed by Pearson [4] is mainly considered. This statistic is based on the discrepancies between the observed and the expected frequencies in the given intervals. Further modifications of the Chi Square test statistic are studied by many authors, as in Best and Rayner [5] [6] .
The initial statistic for goodness of fit test is CH square, then other statistics are considered as a distance between the theoretical and empirical distribution, for details see ref [10] . Test statistics are derived from the sum of discrepancies between the empirical and the hypothetical distribution functions. Among these statistics are the Kolmogrov- Smirnov, Cramer von-Miss and Anderson Darling test statistics. Choulakian [7] modified these statistics for testing a discrete distribution. Spinelli and Stephens [8] have used these statistics for testing the poisson distribution. Spinelli [9] has considered these statistics for testing grouped data fit to the exponential distribution. Baklizi [10] proposed the weighted Kolmogorov test statistics for the Rayleigh interval grouped data. Many other researchers studied the asymptotic distributions of some of these statistics as in Schmid [11] and Pettitt and Stephens [12] . Modifications, critical values and powers of these statistics are also considered for some distributions with grouped data as in Conover [13] , Reidwyl [14] , Maag [15] , Damianou and Kemp [16] , Gulati and Neus [17] , Richard and Lockhart [18] , and Ampai and Kanisa [19] .
As an extension to the Rayleigh distribution, the generalized Rayleigh distribution is used for a more general lifetime data. The probability distribution, the cumulative distribution and the reliability functions of the generalized Rayleigh distribution with scale parameter  and shape parameter
and shape parameter 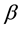 are given respectively by
are given respectively by
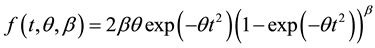 (1)
(1)
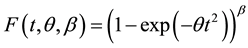 (2)
(2)
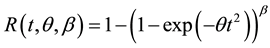 (3)
(3)
where: .
.
Raqab and Kundu [20] showed that this lifetime model can be widely used in survival and reliability analysis. Maximum likelihood estimators for both the scale parameter 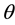 and the shape parameter
and the shape parameter  based on the interval grouped data are obtained by Debasis and Raqabb [21] .
based on the interval grouped data are obtained by Debasis and Raqabb [21] .
The aim of this study is to evaluate performance of the weighted Kolmogrov-Smirnov and the modified Cramer von-Miss and Anderson Darling test statistics for fitting the interval grouped data to the generalized Rayleigh distribution. The test statistics are compared in terms of their powers and controlling of type 1 errors. In the next section the test statistics are derived using the interval grouped data. In Section 3 an extended simulation study is conducted with the original generalized Rayleigh distribution data to find the test statistics that control type 1 error. In Section 4 an alternative data from other lifetime distributions are used in connection with the simulation study to obtain powers of the given test statistics. Results from the simulation study are summarized in Section 5 and finally in Section 6 general conclusion and highlights of the overall finding and future works are also involved.
2. The Test Statistics
Suppose, we have a random sample of size n from the generalized Rayleigh distribution with probability density function given by (1).
Assume that the time scale line is divided by the inspection points 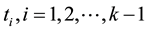
Suppose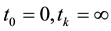 , then we have the intervals
, then we have the intervals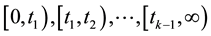 .
.
Let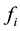 : be the number of failure units in the ith interval,
: be the number of failure units in the ith interval, 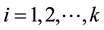 , and assume that
, and assume that 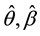 are the maximum likelihood estimators of
are the maximum likelihood estimators of 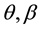 based on the above interval grouped data. Then the empirical and the theoretical distribution functions at the inspection times
based on the above interval grouped data. Then the empirical and the theoretical distribution functions at the inspection times ![]() are respectively
are respectively
![]()
Hence, following Baklizi [10] , the weighted Kolomogorov test statistics are given by
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
where:![]() .
.
Setting: the probability of failure in the corresponding intervals: ![]()
![]()
Then, following Choulakian [7] , the modified Anderson Darling test statistics is given by
![]() (7)
(7)
where: ![]() and
and![]() .
.
And, following Spinelli [9] , the modified Cramer test statistics is given by
![]() (8)
(8)
3. Simulation Study
In this section, an extensive simulation study is conducted to obtain the test statistics that control type 1 error for testing the hypotheses:
H0: the data distribution is the generalized Rayleigh distribution
H1: the data distribution is not the generalized Rayleigh distribution
At the significance level: ![]() with the following indices:
with the following indices:
The sample size: ![]()
The number of intervals: ![]()
The original generalized Rayleigh distribution data with parameters:![]()
The inspection times ![]() are taken to be equally likely spaced.
are taken to be equally likely spaced.
For each combination, the following steps describe the simulation process:
(1) Generate a random sample of size n from the generalized distribution and group it into k intervals
(2) Compute the values of the MLE’s: ![]() based on the interval grouped data
based on the interval grouped data
(3) Compute the values of the test statistics:![]()
(4) Generate a bootstrap sample of size n from the generalized Rayleigh distribution with parameters ![]()
and repeat the steps 2 and 3 to have the new values of the test statistics ![]()
(5) Repeat the step 4, ![]() times and compute the number of values
times and compute the number of values ![]() for which the values of the test statistics found in 4 are greater than the test statistics found in 2 and compute the p value for each statistics as:
for which the values of the test statistics found in 4 are greater than the test statistics found in 2 and compute the p value for each statistics as:
![]() .
.
(6) Repeat the steps 1-5, 1000 times and compute the empirical type 1 error for each statistics as![]() ,
,
where: w = the number of the p values less than the given significance level:![]() .
.
Based on the Bradley [22] test, the test statistics is considered to control type 1 error if the corresponding value of its empirical type 1 error is between 0.025 and 0.075 for the significance level = 0.05.
4. Power of the Test Statistics
To find the empirical power for each of the given test statistics, an alternative non-generalized Rayleigh data are generated in step 1 of the simulation process described in the previous section. Hence, we consider the following distributions:
-One parameter Rayleigh distribution with distribution function:
![]()
-Weibull distribution with distribution function:
![]()
-Generalized Exponential distribution with distribution function:
![]()
5. Results and Conclusions
In this section, found out results about the empirical type 1 error and the power functions of the test statistics are illustrated. Compressions of the test statistics and the affecting factors are also illustrated.
5.1. Controlling of Type 1 Error
The empirical type 1 error rates at the significance level ![]() of the test statistics as applied to the original data are presented in Table 1. It appears clearly that
of the test statistics as applied to the original data are presented in Table 1. It appears clearly that
(1) The test statistics Gv1, Gv3 can control type 1 error for any sample size and any number of inspection intervals.
![]()
Table 1. Empirical type 1 error rates.
*Not control type 1 error.
(2) The test statistic Gv1 cannot control type 1 error for the sample size n = 100 and the number of inspection Intervals k = 5.
(3) The weighted Kolmogrov-Smirnov statistic Gv2 dominate Gv1 and Gv3 when the sample sizes n = 30, 50 and the statistic Gv3 is relatively better than Gv2 when the sample size n = 100.
(4) The Anderson Darling test statistic: Ad cannot control type 1 error for the sample size n = 100 using any number of inspection intervals. But for the sample sizes: n = 30, n = 50 it gives a better controlling of type 1 error than the Cramer von-Miss Cvm test statistic.
(5) Generally, the statistics Gv1, Gv2 and Gv3 have more controlling of type 1 errors than both Cramer von- Miss and Anderson Darling test statistics.
5.2. Power Performance
The powers of the test statistics applied to the nongeneralized Rayleigh grouped data are presented in the tables: Tables 2-7 where we have the following results:
(1) The power functions of the given test statistics increases as the sample size and the number of inspection intervals increases.
(2) For the sample sizes: n = 30 and n = 50, the Anderson Darling test statistic have more power than the Cramer von-Miss test statistic.
(3) Among the weighted Kolmogrov-Smirnov statistics, Gv2 has the greatest power, next came Gv3, and then Gv1.
(4) Generally, the weighted Kolmogrov-Smirnov test statistics have greater power than the Anderson Darling and the Cramer von-Miss test statistics. Except at the sample size 30, the Anderson Darling test statistics gives greater power than Gv1 when the alternative data are considered from the from: the one parameter Rayleigh distribution with scale parameter![]() , the Weibull distribution with scale Parameter
, the Weibull distribution with scale Parameter ![]() and shape parameter
and shape parameter ![]() and the generalized exponential distribution with scale parameter
and the generalized exponential distribution with scale parameter ![]() and shape parameter
and shape parameter![]() .
.
![]()
Table 2. Power of the test statistics for the interval grouped data from the one parameter Rayleigh distribution with scale parameter θ = 0.85.
![]()
Table 3. Power of the test statistics for the interval grouped data from the one parameter Rayleigh distribution with scale parameter θ = 0.05.
![]()
Table 4. Power of the test statistics for the interval grouped data from the Weibull distribution with scale parameter θ = 0.65, and shape parameter β = 1.8.
![]()
Table 5. Power of the test statistics for the interval grouped data from the Weibull distribution with scale parameter θ = 0.05, and shape parameter β = 0.3.
![]()
Table 6. Power of the test statistics for the interval grouped data from the generalized exponential distribution with scale parameter θ = 1.5 and shape parameter β = 1.
![]()
Table 7. Power of the test statistics for the interval grouped data from the generalized exponential distribution with scale parameter θ = 0.05 and shape parameter β = 2.5.
(5) There is a significant affection in the power of the test statistics in fitting the generalized Rayleigh distribution with shape parameter ![]() for the lifetimes data. This affection clearly appears when using the alternatives: the one parameter Rayleigh and the generalized exponential distributions
for the lifetimes data. This affection clearly appears when using the alternatives: the one parameter Rayleigh and the generalized exponential distributions
(6) The powers of the test statistics are mainly affected by the parameters of the alternative distributions, when the alternative Weibull distribution with scale parameter ![]() and shape parameter
and shape parameter ![]() is considered, the values of the power functions are strictly less than their corresponding values when the alternative is the Weibull distribution with scale parameter
is considered, the values of the power functions are strictly less than their corresponding values when the alternative is the Weibull distribution with scale parameter ![]() and shape parameter
and shape parameter![]() .
.
A possible explanation for this is the degree of similarity between the Weibull distribution and the Generalized Rayleigh distribution when using a complete data at the indicated parameters.
6. Conclusion and Highlights for Future Work
This study explored the performance of goodness of fit test statistics for the generalized Rayleigh distribution. Generally, the weighted Kolmogrov-Smirnov test statistics have a relatively better performance in controlling type 1 error and in the power functions than the modified Cramer von-Miss and Anderson Darling test statistics. As it cannot control type 1 error when the sample size n = 100, the Anderson Darling test has more power than the Cramer von-Miss and the weighted Kolmogrov-Smirnov Gv1 test statistics when the sample size n = 30 or n = 50. This indicates that the researcher has to take into account both the sample size and number of inspection intervals when choosing the test statistic for fitting the interval grouped data to the generalized Rayleigh distribution. Future works may involve other lifetime models in the presence of censoring schemes within the intervals. Critical regions for the test statistics at different significance levels can also be a subject of concern.