Forecasting Short Time Series with Missing Data by Means of Energy Associated to Series ()
1. Introduction
Time series forecasting recently has a preponderant significance in order to know the best behavior of a system in study such as the availability of estimated scenarios for water predictability [1] , the rainfall forecast problem [2] [3] in some geographical points of Cordoba, the energy demand purposes [4] , and the guidance of seedling growth [5] . For general feed-forward neural networks [6] - [8] , the computational complexity of these solutions grows exponentially with the number of missing features. In this paper we describe an approximation for the problem of missing information that is applicable to a large class of learning algorithms [9] [10] , including ANN’s. One major advantage of the proposed solution is that the complexity does not increase with an increasing number of missing inputs. The solutions can easily be generalized to the problem of uncertain (noisy) inputs.
The problem of missing data poses a difficulty to the analysis and decision making processes which depend on this data, requiring methods of estimation which are accurate and efficient. Various techniques exist as a solution to this problem, ranging from data deletion to methods employing statistical and artificial intelligence techniques to impute for missing variables [11] . However, in this work, a linear estimation is employed making assumptions about the data that may not be true, affecting the quality of decisions made based on this data. The estimation of missing data in vector elements in real-time processing applications requires a system that possesses the knowledge of certain characteristics such as correlations between variables, which are inherent in the input space [12] . Those are taken from the Mackay Glass benchmark equation and cumulative historical rainfall whose forecast is simulated by a Monte Carlo approach employing ANN. The main contribution here is the design of a forecast system that uses incomplete data sets for tuning its parameters, and at the same time the historical recorded data are relatively short. The filter parameter is put in function of the roughness of the short time series, between its smoothness. In addition, this forecasting tool is intended to be used by agricultural producers to maximize their profits, avowing profit losses over the misjudgment of future movements to maximize their utilities. A one-layered feed-forward neural network, trained by the Levenberg-Marquardt algorithm is implemented in order to give the next 15 values. The paper is organized as follows: Section 2 introduces the data used for the algorithm. Section 3 describes an important issue to forecast with small datasets. Section 4 summarizes the implementation of the energy associated approach. In Section 5, prediction results are shown for a class of high roughness time series, namely short-term chaotic time series with a forecast horizon of 15 steps. Lastly, in Section 6 some discussion and conclusion are drawn.
2. Data Treatment
2.1. Rainfall Data and Neural Network Pattern Modeling
In this work the Hurst’s parameter is used to determine the long-short term stochastic dependence of the rainfall time series. Besides, the neural network algorithm modifies in the learning process on-line the number of patterns, the number of iterations, and the number of filter’s inputs. The definition of the Hurst’s parameter appears in the Brownian motion from generalizing the integral to a fractional one. The Fractional Brownian Motion (fBm) is defined in the pioneering work by Mandelbrot [13] through its stochastic representation:
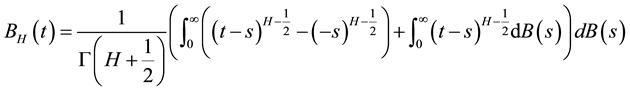 (1)
(1)
The fBm is self-similar in distribution and the variance of the increments is defined by:
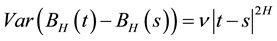 (2)
(2)
where 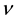 is a positive constant.
is a positive constant.
2.2. San Agustin Rainfall Data
The dataset chosen is from historical data 2004 to 2011 from San Agustin, located at Cordoba, Argentina shown in Figure 1. The original dataset (AGUS) used is incomplete and contains 51 data of cumulative monthly rainfall data, in which there are 14 months values incomplete resulting in a non-determinist series, respectively. This kind of behavior is difficult to predict because seasonality is not well-determined by few data. For the sake of making a fair prediction, a linear smoothing was employed to replace the incomplete data. This consists of averaging on vertical column shows in Figure 2, the prior and posterior value that corresponds to the same year.
2.3. Mackay-Glass Time Series
The second benchmark of series is obtained from solution of the MG equation. This equation serves to model natural phenomena and has been used in earlier work to implement different methods of comparison to make forecast [14] , which is explained by the time delay differential MG equation [15] , defined as
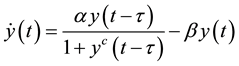 (3)
(3)
where α, β varies and c = 10 are parameters and τ = 100 is the delay time. According as τ increases, the solution turns from periodic to chaotic. Thereby, a time series with a random-like behavior is obtained, and the long-term behavior changes thoroughly by changing the initial conditions to obtain the stochastic dependence of the deterministic time series according to its roughness [16] .
In this work the Hurst’s parameter is used in the learning process to modify on-line the number of patterns, the number of iterations, and the number of filter’s inputs of the ANN. This H serves to have an idea of roughness
![]()
Figure 1. Cumulative monthly rainfall of san agustin (AGUS) with incomplete data, Cordoba, Argentina.
![]()
Figure 2. Average technique adopted to complete the rainfall dataset.
Figure 2. Average technique adopted to complete the rainfall dataset.
of a signal [17] [18] and the time series are considered as a trace of an fBm depending on the so-called Hurst parameter 0 < H < 1 [19] . The MG benchmark chosen are called MG17 with τ = 17, MG085, MG1.6 and MG1.9.
3. Problem Formulation
The main issue when forecasting a time series is how to retrieve the maximum of information from the available data [20] . In this case, the lack of data in the dataset is taken into account in order to predict one step ahead for the filter based on ANN. It is proposed to fill these empty values by using prior and posterior data. Four dataset are built following Figure 2. In the first one, the lack data is completed by taking the same ensemble of data of the past year. The second one by using the same ensemble of the next year, the third one is completed with zeros and lastly is filled in by averaging the prior and posterior year. The same analogy is used to construct MG17, MG0.85, MG1.9 and MG1.6 dataset solution of (3).
The coefficients of the ANNs filter are adjusted on-line in the learning process, by considering a criterion that modifies at each pass of the time series the number of patterns, the number of iterations and the length of the tapped-delay line, in function of the Hurst’s value (H) calculated from the time series according to the stochastic behavior of the series, respectively.
In this work, the present value of the time series is used as the desired response for the adaptive filter and the past values of the signal serve as input of the adaptive filter [21] . Then, the adaptive filter output will be the one-step prediction signal. In the block diagram of the nonlinear prediction scheme based on an ANN filter is shown. Here, a prediction device is designed such that starting from a given sequence {xn} at time n corresponding to a time series it can be obtained the best prediction {xe} for the following sequence of 15 values. Hence, it is proposed a predictor filter with an input vector lx, which is obtained by applying the delay operator, Z−1, to the sequence {xn}. Then, the filter output will generate xe as the next value, that will be equal to the present value xn. So, the prediction error at time k can be evaluated as
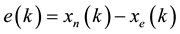 (4)
(4)
4. Proposed Approach to Calculate the Energy Associated of Series
Approximation by Primitive of Integration
The area resulting of integrating the data time series of MG and rainfall data series is the primitive, that is obtained by considering each value of time series its derivate [22] ;
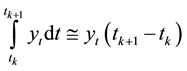 (5)
(5)
where yt is the original value time series. The area approximation by its periodical primitive is:
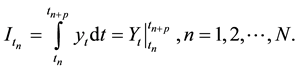 (6)
(6)
During the learning process, those primitives are calculated as a new entrance to the ANN, in which the prediction attempts to even the area of the forecasted area to the primitive real area predicted. The real primitive integral is used in two instances, firstly from the real time series an area is obtained and run by the algorithm proposed. The H parameter from this time series is called HA. On the other hand, the data time series is also forecasted by the algorithm, so the H parameter from this time series is called HS. Finally, after each pass the number of inputs of the nonlinear filter is tuned―that is the length of tapped-delay line, according to the following heuristic criterion. After the training process is completed, both sequences―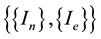 and
and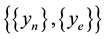 ―in accordance with the hypothesis that should have the same H parameter. If the error between HA and HS is greater than a threshold parameter θ the value of lx is increased (or decreased), according to lx ± 1. Explicitly,
―in accordance with the hypothesis that should have the same H parameter. If the error between HA and HS is greater than a threshold parameter θ the value of lx is increased (or decreased), according to lx ± 1. Explicitly,
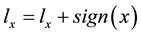 (7)
(7)
Here, the threshold θ was set about 1%.
5. Prediction Results
5.1. Generations of Areas from Benchmark
Primitives of time series are obtained from sampling the MG equations with parameters shown in Table 1, with t = 100, c = 10 and varying β, α. This collection of coefficients was chosen to generate time series whose H parameters vary between 0 and 1 (Table 2). In fact, the chosen ones were selected in accordance with their roughness.
5.2. Performance Measure for Forecasting
In order to test the proposed design procedure of the ANN-based nonlinear predictor, an experiment with time series obtained from the MG solution was performed. The performance of the filter is evaluated using the Symmetric Mean Absolute Percent Error (SMAPE) proposed in the most of metric evaluation, defined by
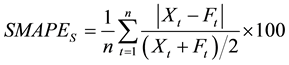 (8)
(8)
where t is the observation time, n is the size of the test set, s is each time series, Xt and Ft are the actual and the forecasted time series values at time t respectively. The SMAPE of each series s calculates the symmetric absolute error in percent between the actual Xt and its corresponding forecast value Ft, across all observations t of the test set of size n for each time series s.
5.3. Forecasting Results
Each time series is composed by samples of MG solutions and San Agustin rainfall time series. Three classes of data sets are used. The first one is the original time series used by the algorithm to train the predictor filter, which comprises 35 values. The next one is the primitive obtained by integrating the original time series data. The last one is used to compare if the forecast is acceptable or not, in which the last 15 of 50 values can be used to validate the performance of the prediction system. A comparison of roughness measured by the H parameter is made between AGUS rainfall and MG series.
The Monte Carlo method was used to forecast the next 15 values from San Agustin rainfall series (AGUS), MG085, MG1.6, MG1.9 and MG17 time series and their primitive. Such outcomes are shown from Figure 3 to Figure 7. The plot shown in Figure 3(a), Figure 4(a), Figure 5(a), Figure 6(a) and Figure 7(a) are from H dependent ANN predictor filter. Figure 3(b), Figure 4(b), Figure 5(b), Figure 6(b) and Figure 7(b) are obtained by the energy associated approach.
The algorithm achieves the long or short term stochastic dependence measured by the Hurst parameter in order to make more precisely the prediction. The forecasted time series area is put as a new entrance to the ANN and serves to be compared with the real primitive obtained of the time series.
The figures show a class of high roughness time series selected from a benchmark of MG Equation and compared with AGUS rainfall series. These are classified by their statistically dependency, so the algorithm is adjusted by depending on the H parameter. At Table 3 and Table 4 shows a good performance seen from the
![]()
Table 1. Parameters to generate the mg times series.
![]()
Table 2. Parameter of San Agustin rainfall series.
![]()
![]() (a) (b)
(a) (b)
Figure 3. Non-linear autoregressive predictor filter. (a) H dependent neural network algorithm for MG085; (b) Energy asscociated approach for MG085.
![]()
![]() (a) (b)
(a) (b)
Figure 4. Non-linear autoregressive predictor filter. (a) H dependent neural network algorithm for MG1.9; (b) Energy asscociated approach for MG1.9.
![]()
![]() (a) (b)
(a) (b)
Figure 5. Non-linear autoregressive predictor filter. (a) H dependent neural network algorithm for MG1.6; (b) Energy asscociated approach for MG1.6.
![]()
![]() (a) (b)
(a) (b)
Figure 6. Non-linear autoregressive predictor filter. (a) H dependent neural network algorithm for MG17; (b) Energy asscociated approach for MG17.
![]()
![]() (a) (b)
(a) (b)
Figure 7. Non-linear autoregressive predictor filter. (a) H dependent neural network algorithm for AGUS rainfall series; (b) Energy asscociated approach for AGUS rainfall series.
![]()
Table 3. Comparisons obtained by the neural network H dependant predictor filter.
![]()
Table 4. Comparisons obtained by the energy associated approach.
SMAPE index of in AGUS rainfall series and MG1.6 series when they take into accounts the roughness of the series considering the use of the stochastic dependence measured by the H parameter.
6. Discussion and Conclusions
In this work, short-term rainfall time series prediction with incomplete data by means of energy associated of series was presented. The learning rule proposed to adjust the ANNs weights is based on the Levenberg- Marquardt method and energy associated to series as a new input. Likewise, in function of the short-term stochastic dependence of the time series evaluated by the Hurst parameter H, the performance of the proposed filter shows that even the short dataset is incomplete, besides a linear smoothing technique employed, the prediction is almost good. The major result shows that the predictor system based on energy associated to series has an optimal performance from several samples of MG equations and, in particular, MG1.6 and AGUS rainfall time series. These were considered as a path of a fractional Brownian motion [19] whose H parameter measured is a high roughness signal, which is assessed by HS and HA, respectively. Although the comparison was only performed on ANN-based filters, the experimental results confirm that the energy associated to series method can predict short-term rainfall time series more effectively in terms of SMAPE indices when compared with other existing forecasting methods in the literature.
This approach encourages forecasting meteorological variables such as moisture soil series, daily and hour rainfall and water runoff when the observations are taken from a single point.
Acknowledgements
This work was supported by Universidad Nacional de Córdoba (UNC), FONCYT-PDFT PRH No. 3 (UNC Program RRHH03), SECYT UNC, Universidad Nacional de San Juan―Institute of Automatics (INAUT), National Agency for Scientific and Technological Promotion (ANPCyT) and Departments of Electronics―Electrical and Electronic Engineering―Universidad Nacional of Cordoba.