Implementation of the Estimating Functions Approach in Asset Returns Volatility Forecasting Using First Order Asymmetric GARCH Models ()
1. Introduction
Asset return volatility is an imperative factor in pricing of derivatives and portfolio allocation in the financial world. As a result, many conventional methods for measuring the risk associated with financial assets are done through studies on the variance (volatility) of the asset price [1] . Volatility is considered as a measure of risk which is used by investors as a premium for investing in risky assets and therefore an efficient model for forecasting an asset’s price volatility is a crucial ingredient in financial decision making.
The GARCH family of models and their extensions have proved through empirical evidence, to be successful in explaining the dynamics of return volatility in the financial markets. This has led to their extensive application to modelling and forecasting stock market returns volatility, in developed economies [2] - [5] as well as in emerging markets [6] - [10] .
Consequently, much attention has been paid to the estimation of this class of models in a bid to provide an efficient framework for modelling and forecasting return volatility. Different approaches among them, the maximum likelihood (ML), the estimating functions (EF) and the Bayesian adaptive Markov chain Monte Carlo (MCMC) methods, have been utilized in estimation of the symmetric/asymmetric GARCH models and volatility prediction [11] - [13] . An efficient estimation method translates to an improved predictive ability of the model. The ultimate goal of volatility analysis must be to explain the causes and predict future volatility values.
The focus of this paper is to implement the method of estimating functions based on [14] ’s optimal estimating functions for stochastic processes, in the asset return volatility prediction in the Asymmetric GARCH family of models. First order EGARCH and GJR-GARCH models estimated in [13] are utilised in forecasting asset return volatility of empirical time series from the USA and Japanese stock markets. A brief overview of the first order EGARCH and GJR-GARCH models is presented in Section 2. Optimal estimating functions for the Asymmetric GARCH―class of models in general and the first order EGARCH and GJR-GARCH models are presented in Section 3. Forecast ability of the two first order Asymmetric GARCH models is evaluated in Section 4. Finally, a conclusion of this paper is presented in Section 5.
2. GARCH Models with Asymmetry
There is extensive empirical evidence that stock returns exhibit asymmetric volatility, that is, there is existence of asymmetric effects of positive and negative past returns on volatility [15] - [18] . To model this aspect, this paper considers two of the most popular asymmetric GARCH models.
2.1. EGARCH Model
The EGARCH model by [19] addresses some of the key limitations of the conventional GARCH model. This model captures asymmetric responses of the conditional variance to shocks in the market. The EGARCH 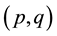 is specified as;
is specified as;
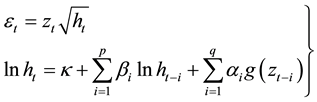 (1)
(1)
where,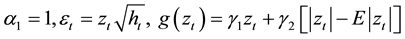 .
.
The model specifies the variance equation as the log of the variance series hence the leverage effect is exponential and therefore the parameters 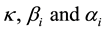 are not restricted to be non-negative.
are not restricted to be non-negative. 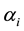 is the asymmetry parameter.
is the asymmetry parameter.
The quantity 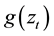 is a function of both magnitude and sign of
is a function of both magnitude and sign of 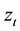 in order to accommodate the asymmetric effect [19] . The components
in order to accommodate the asymmetric effect [19] . The components 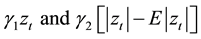 represent the sign effect and magnitude effect respectively and each has a zero mean.
represent the sign effect and magnitude effect respectively and each has a zero mean.
Over the range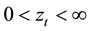 ,
, 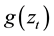 is linear in
is linear in 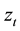 with slope
with slope 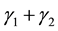 while over the range
while over the range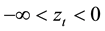 ,
, 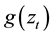 is linear in
is linear in 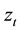 with slope
with slope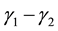 . Thus
. Thus ![]() allows the conditional variance
allows the conditional variance ![]() to respond asymmetrically to changes in stock returns.
to respond asymmetrically to changes in stock returns.
2.2. GJR-GARCH Model
The GJR-GARCH model was introduced by [20] . It is a variant of the GARCH model with the ability to capture asymmetries between positive and negative shocks of the same magnitude on the volatility of returns. The variance equation in GJR-GARCH ![]() model is specified as;
model is specified as;
![]() (2)
(2)
where,![]() .
.
The model reduces to the traditional GARCH model whenever![]() . The indicator term
. The indicator term ![]() captures the asymmetric effect of past returns on current volatility. With
captures the asymmetric effect of past returns on current volatility. With ![]() negative shocks
negative shocks ![]() increase volatility more than positive shocks
increase volatility more than positive shocks ![]() of equal magnitude. The necessary and sufficient conditions to guarantee positivity of the conditional variance
of equal magnitude. The necessary and sufficient conditions to guarantee positivity of the conditional variance ![]() are
are ![]()
![]() is the asymmetry parameter.
is the asymmetry parameter.
3. Estimation of the Asymmetric GARCH Models Using Estimating Functions
In this section we state some important results on estimating functions for the asymmetric GARCH models. [13] derived the optimal estimating functions for the Asymmetric Garch family of models, based on the works of [21] and [14] . The optimal EFs as presented in [13] are given in (3)
![]() (3)
(3)
where, ![]() is the conditional variance process given in (1) and (2). The estimates for the unknown parameter vectors
is the conditional variance process given in (1) and (2). The estimates for the unknown parameter vectors ![]() and
and ![]() are obtained by solving the optimal EFs in (3) by numerically minimising
are obtained by solving the optimal EFs in (3) by numerically minimising![]() .
.
First order EGARCH and GJR-GARCH models have been fitted to the Standard and Poor’s 500 and the Nikkei 225 market indices for the period 2nd Jan 2008 to 31st May 2011. The estimated models under the EFs approach are presented in (4), (5), (6) and (7).
S&P 500 index
![]() (4)
(4)
![]() (5)
(5)
Nikkei 225 index
![]() (6)
(6)
![]() (7)
(7)
where, ![]() and
and![]() .
.
The time plots of the estimated conditional variance series in (4), (5), (6) and (7) are given in Figures 1-4 respectively.
![]()
Figure 1. Time plot of the estimated conditional variance in (4).
![]()
Figure 2. Time plot of the estimated conditional variance in (5).
![]()
Figure 3. Time plot of the estimated conditional variance in (6).
![]()
Figure 4. Time plot of the estimated conditional variance in (7).
The time plots in Figures 1-4 indicate that the estimated conditional variance is extremely high for some periods and relatively low in others (time variant) which is a common feature in most financial data.
4. Forecasting the Volatility of Financial Asset Returns of the USA and Japan Stock Markets
The fitted models under the EF approach have been used for forecasting the daily volatility of stock returns for the S&P 500 index and Nikkei 225 index data sets. Out-of-Sample forecasting is performed for the period (1st June 2011 to 13th October 2012).
Forecasts for the first order EGARCH and GJR-GARCH conditional variance processes over m = 500 days (future time horizon) have been generated. Given the log conditional variance process ![]() for the EGARCH and conditional variance process
for the EGARCH and conditional variance process ![]() for the GJR-GARCH model, predictions for
for the GJR-GARCH model, predictions for ![]() and
and ![]() have been generated for the forecast period m = 500.
have been generated for the forecast period m = 500.
The conditional variance ![]() is time varying (volatile) and is the object of interest in the forecasting process. In the case that only daily closing prices are available, the daily squared returns is an appropriate proxy for the unobserved volatility that fully accounts for the time varying property. The daily squared returns have for long and widely been used as a proxy of the latent realized variance [22] . In this study, the daily squared returns over the forecast period have been used as a proxy for the unobserved variance which is incorporated in the loss functions used to generate the error statistics used for evaluating the predictive ability of the two first order asymmetric GARCH models.
is time varying (volatile) and is the object of interest in the forecasting process. In the case that only daily closing prices are available, the daily squared returns is an appropriate proxy for the unobserved volatility that fully accounts for the time varying property. The daily squared returns have for long and widely been used as a proxy of the latent realized variance [22] . In this study, the daily squared returns over the forecast period have been used as a proxy for the unobserved variance which is incorporated in the loss functions used to generate the error statistics used for evaluating the predictive ability of the two first order asymmetric GARCH models.
The time plots of the daily squared returns over the forecast period![]() , for the two data sets are given in Figure 5 and Figure 6.
, for the two data sets are given in Figure 5 and Figure 6.
The following two loss functions have been used to evaluate the out-of-sample forecast performance of the models. They include the Mean Square Error (MSE) and the Mean Absolute Error (MAE).
![]() (8)
(8)
![]() (9)
(9)
![]()
Figure 5. Time plot of the daily squared returns for the S&P 500 index.
![]()
Figure 6. Time plot of the daily squared returns for the Nikkei 225 index.
where, m is the number of days in the out-of-sample period, ![]() is the proxy of the actual volatility and
is the proxy of the actual volatility and ![]() is the volatility forecast at day t. The loss functions have been used to compute forecasts errors of the models.
is the volatility forecast at day t. The loss functions have been used to compute forecasts errors of the models.
Table 1 presents the forecasts error statistics used to evaluate the forecast performance of the models.
The forecast ![]() at time t is used in computing the forecast
at time t is used in computing the forecast ![]() at time
at time![]() , for
, for ![]() due to the recursive nature of these models. It is observed that as the forecasts are generated recursively, the recursion converges asymptotically to the theoretical unconditional variance of the processes.
due to the recursive nature of these models. It is observed that as the forecasts are generated recursively, the recursion converges asymptotically to the theoretical unconditional variance of the processes.
For the EGARCH (1,1) process the unconditional variance is given in (10).
![]() (10)
(10)
For the GJR-GARCH (1,1) process the unconditional variance is given in (11).
![]() (11)
(11)
Time plots of the conditional variance forecast asymptotes for the two models and data sets are given in Figures 7-10.
Figure 7 and Figure 8 present the conditional variance forecast asymptotes of the two models for the S&P 500 index data set. Figure 9 and Figure 10 present the conditional variance forecast asymptotes of the two models for the Nikkei 225 index data set.
It is observed that for the S&P 500 index, the volatility forecasts converge asymptotically to the unconditional variance (0.000182, 0.0002003) after about (282, 263) data points for the EGARCH (1,1) and GJR-GARCH (1,1) processes respectively. For the Nikkei 225 index, the volatility forecasts converge asymptotically to the unconditional variance (0.0002045, 0.0002412) after about (216, 154) data points for the EGARCH (1,1) and GJR- GARCH (1,1) processes respectively.
Discussion
The out-of-sample fit of the two models is evaluated using the MSE and MAE statistics. There is no specific
model that is preferred based on both loss functions as mixed results are obtained across the two data sets (see Table 1). However considering the MSE, the first order EGARCH model provides the best out-of-sample volatility forecast than the GJR-GARCH model. The more robust loss function, MAE indicates that the first order GJR-GARCH model performs better but for only one data set, S&P 500 index. Thus the ranking of models in terms of forecast performance based on a specific loss function varies across the two data sets over the considered forecast period. This inconsistency in ranking stresses the importance of selecting an adequate loss function for forecasting purposes. The two models forecast a general increase in conditional variance before the processes converge to the theoretical unconditional variances. Figure 8 and Figure 10 show that the first order GJR- GARCH process forecasts converge faster to the unconditional variance than the corresponding EGARCH process forecasts (see Figure 7 and Figure 9) implying that the latter process has a higher forecast memory.
5. Conclusion
In this paper the main objective was to implement the method of optimal estimating functions in volatility estimation and prediction using Asymmetric GARCH modes. First order EGARCH and GJR-GARCH models have then been used in forecasting asset volatility of the USA and Japan stock markets using the S&P 500 and Nikkei 225 indices respectively under the EF approach. The two models have recorded mixed out-of-sample forecast performance results across the data sets. However the MSE and MAE statistics are generally lower for the EGARCH model across the two data sets except for a single case where the GJR-GARCH model records a lower MAE for the S&P 500 index data set. Thus first order EGARCH model performed relatively better than the first order GJR-GARCH model in forecasting volatility over the considered forecast period.
Acknowledgements
This research paper was prepared and made possible through the help and support of my academic supervisors,
The German Academic Exchange Service (DAAD) and the African Mathematics Millennium Science Initiative
![]()
Table 1. Forecast error statistics for EGARCH and GJR-GARCH models.
![]()
Figure 7. Time plot of the EGARCH (1,1) conditional variance forecast asymptote.
![]()
Figure 8. Time plot of the GJR-GARCH (1,1) conditional variance forecast asymptote.
![]()
Figure 9. Time plot of the EGARCH (1,1) conditional variance forecast asymptote.
![]()
Figure 10. Time plot of the GJR-GARCH (1,1) conditional variance forecast asymptote.
(AMMSI) who sponsored my postgraduate studies.