Fundamental Physical Basis for Maxwell-Heaviside Gravitomagnetism ()
1. Introduction
“The world which we have to build from the crude material is the world of perception,
and the process of building must depend on the nature of the percipient.”
―Sir Arthur S. Eddington (1882-1944)
The first to consider the possibility of a formal analogy between gravitation and electromagnetism is the great and pre-eminent Scottish physicist―Professor James Clerk Maxwell (1831-1879), in his landmarking treatise on “A Dynamical Theory of the Electromagnetic Field” [1] . After failing to justify (to himself) the implied negative energies associated with the gravitational field, Professor Maxwell abandoned this line of thought [2] . Twenty eight years had to pass before Dr. Oliver Heaviside (1850-1925) reconsidered Professor Maxwell’s imaginative and brilliant but forgotten thoughts [3] [4] . Despite its brilliance and fit of imagination, both Professor Maxwell [1] and Dr. Heaviside [3] [4] ’s work was speculative with no real justification from the then known fundamental principles of either physics or logic but rather from the intuitive power of human reason and imagination. Only in recent times, there is a justifiable fundamental physical basis for Professor Maxwell and Dr. Heaviside’s speculation (hereafter, the Maxwell-Heaviside Gravitomagnetic Theory) which has been heralded [2] [5] [6] .
Writing in his book “Causality, Electromagnetic Induction and Gravitation”, Professor Oleg D. Jefimenko (1922-2009) revived [5] this almost forgotten if not abandoned line of thought which most now is viewed as a pseudo-science because of the lack of a real fundamental physical and theoretical justification save for the sheer power and wit of human intuition and imagination. Taking the work of Professor Jefimenko one important and crucial step further, Professor José Hera [6] formulated an important Existence Theorem that states that, given any space and time-dependent localized scalar and vector sources satisfying the continuity equation―as is the case with gravitation and electromagnetism, there are two retarded fields that satisfy a set of four field equations. By applying the theorem to the usual electromagnetic charge and current densities, the retarded fields are identified with the electric and magnetic fields and the associated field equations with Maxwell’s equations. In a nutshell, what Professor José Hera [6] proved is that, if ρ is the charge density, J is the associated current corresponding to this charge, and the conservation law is satisfied i.e.:
 (1)
(1)
then, there must be two corresponding fields, 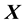 and
and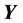 , which satisfy the following set of equations:
, which satisfy the following set of equations:
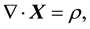 (2)
(2)
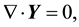 (3)
(3)
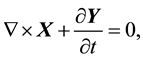 (4)
(4)
 (5)
(5)
where α, β, γ are arbitrary positive constants and are related to the speed of light c by the equation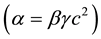 . In the case of electricity and magnetism, if X and Y are identified with the electric and magnetic fields respectively, then, we will have Professor Maxwell’s classical equations for electrodynamics―in which case
. In the case of electricity and magnetism, if X and Y are identified with the electric and magnetic fields respectively, then, we will have Professor Maxwell’s classical equations for electrodynamics―in which case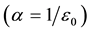 ,
, 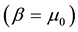 and
and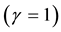 . Clearly, this axiomatic approach of deriving Maxwell’s field equations strongly suggests that electric charge conservation and nothing else can be considered to be the most fundamental assumption underlying Maxwell’s equations of electrodynamics.
. Clearly, this axiomatic approach of deriving Maxwell’s field equations strongly suggests that electric charge conservation and nothing else can be considered to be the most fundamental assumption underlying Maxwell’s equations of electrodynamics.
Unfortunately, Professor José Hera [6] did not consider gravitation in his work. This work by Professor José Hera [6] can be extended not only to gravitation but to any field whose charge and corresponding current obey the continuity equation. Assuming that mass is identified with the gravitational charge of the body in question― as is the case in physics, and also assuming the conservation of mass, which in turn means the conservation of gravitational charge, then there must be two vector fields (call them g and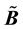 ) that satisfy a set of four Maxwell-type equations. These four equations describe what is known as gravitomagnetism. In this way, gravitomagnetism emerges as a phenomenon that is independent of Einstein’s GTR. Gravitomagnetism is currently an accepted paradigm of gravitation that is accepted on the basis of Einstein’s GTR as a weak field approximation [7] -[14] . We argue that, free from the GTR, the gravitomagnetic phenomenon has a just, secure, and above all― independent existence from the GTR.
) that satisfy a set of four Maxwell-type equations. These four equations describe what is known as gravitomagnetism. In this way, gravitomagnetism emerges as a phenomenon that is independent of Einstein’s GTR. Gravitomagnetism is currently an accepted paradigm of gravitation that is accepted on the basis of Einstein’s GTR as a weak field approximation [7] -[14] . We argue that, free from the GTR, the gravitomagnetic phenomenon has a just, secure, and above all― independent existence from the GTR.
In closing the present section, we give the synopsis of the paper. In Section 2, we give the fundamental basis for why gravitomagnetism must exist. In Section 3, we suggest a source for gravitomagnetic waves. In Section 5, we demonstrate that gravitomagentic waves must travel at the speed of light c. In Section 6, we fit in the Lorenz gauge into the present gravitomagnetic framework. Lastly, in Section 7, we give a general discussion and conclusion drawn. Here at the penultimate, we must state clearly that in this reading, we do not explore the resulting theory, i.e., test is predictions based on already well-known gravitational anomalies―this task we have left for future readings.
2. Gravitomagnetism
Without any doubt, the Hera Existence Theorem [6] justifies the physical need and the existence of gravitomagnetism. Here, we give an exposition of Professor Behera [2] ’s more physical approach to justify gravitomagnetism. Well outside the domains and confines of Einsteinian gravitation, using only Poisson-Laplace equation for the gravitational field (6) and, the law of conservation of mass (9), Professor Behera [2] demonstrated that one can conclusively justify on a fundamental physical level, the inclusion of a vector field, 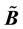 , that is associated with the gravitational field,
, that is associated with the gravitational field, . The Poisson-Laplace equation for the gravitational field is given by:
. The Poisson-Laplace equation for the gravitational field is given by:
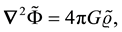 (6)
(6)
where;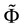 , is the gravitational potential;
, is the gravitational potential;![]() , is mass density of given mass distribution; G, is Newton’s universal constant of gravitation and;
, is mass density of given mass distribution; G, is Newton’s universal constant of gravitation and;![]() , is the three Laplacian operator. For our purposes we shall write the Poisson-Laplace Equation (6), as:
, is the three Laplacian operator. For our purposes we shall write the Poisson-Laplace Equation (6), as:
![]() (7)
(7)
where, ![]() (for now, latter we will add the gravitomagnetic term) and; the universal and fundamental physical constant,
(for now, latter we will add the gravitomagnetic term) and; the universal and fundamental physical constant,![]() :
:
![]() (8)
(8)
is the gravitational permittivity of free space. It is universally accepted that the conservation of mass is always at play everywhere and every-time in the Universe, so, it (the mass continuity equation) holds simultaneously with the Poission-Laplace equation thus, one can―as shall be done shortly, solve these two equations simultaneously. A part of the notation to be used hereafter, it is important that in line with the notation used in the reading [15] we shall, as we have done above, insert a tilde over all quantities that are associated with the gravitomagnetic field and a hat over all quantities associated with the electromagnetic field.
Now, to demonstrate Professor Behera [2] ’s thesis, we start from the Poisson-Laplace Equation (7) and solve this equation simultaneously with the equation of conservation of mass, namely:
![]() (9)
(9)
where, ![]() , is the momentum density: in this expression,
, is the momentum density: in this expression,![]() ; v is the velocity of the material whose density is
; v is the velocity of the material whose density is![]() . We know from (7) that
. We know from (7) that![]() , and from this fact, it follows that:
, and from this fact, it follows that:
![]() (10)
(10)
hence:
![]() (11)
(11)
Now, it is a bona fide mathematical fact that for any general, smooth, differentiable and uniform continuous vector field, say![]() , the following holds true always:
, the following holds true always:
![]() (12)
(12)
where ![]() is a constant that has been inserted for convenience purposes. By comparing (11) and (12), it follows that:
is a constant that has been inserted for convenience purposes. By comparing (11) and (12), it follows that:
![]() (13)
(13)
where, analogously, as the speed of light:
![]() (14)
(14)
is the speed of the resulting gravitomagnetic waves. This speed is not necessarily equal to the speed of light. However, most approaches in gravitomagnetism ad hocly set this speed to equal the speed of light without any real fundamental physical justification but as part and parcel of the formal analogue with Maxwellian electrodynamics. In §(5), we will show that a proper consideration of facts at-hand within the gravitomagnetic framework, invariably set this speed to equal the speed of light, c. It is our view that this achievement in Section 5 of demonstrating that ![]() is indeed, a noteworthy event. We have never come across gravitomagnetic theories that demonstrate that
is indeed, a noteworthy event. We have never come across gravitomagnetic theories that demonstrate that![]() , but this, as aforementioned, is only assumed as part and parcel of the formal analogue with Maxwellian electrodynamics, hence our saying that the achievement in Section 5 of demonstrating that
, but this, as aforementioned, is only assumed as part and parcel of the formal analogue with Maxwellian electrodynamics, hence our saying that the achievement in Section 5 of demonstrating that ![]() may indeed be a noteworthy event.
may indeed be a noteworthy event.
Notice that in (13), we have two options “±”. Which of the two corresponds to reality? Certainly, since there can only be one Universe, only one of the two options “±”, and not both, will correspond to reality. To answer this question, Professor Behera [2] appeals to Maxwell’s electromagnetic theory via the usual way of making a formal analogy, where upon he arrives at the conclusion that the “+” options is what most certainly corresponds to reality. However, one can make the choice by asking which of the two options will lead to a wave solution for the ![]() -field? The answer one gets is the same as that obtained by Professor Behera [2] . The option “+” results in a wave equation for the
-field? The answer one gets is the same as that obtained by Professor Behera [2] . The option “+” results in a wave equation for the ![]() -field while the other option does not. Since we expect waves for the
-field while the other option does not. Since we expect waves for the ![]() -field, it follows that we have to choose the option “+” as the one that corresponds to reality.
-field, it follows that we have to choose the option “+” as the one that corresponds to reality.
Now, at this point we have to ask what does (13) really mean? This equation is a direct logical consequence of the Poisson-Laplace Equation (7) and the continuity Equation (9). Without any doubt, (13) points directly to the undeniable fact that the gravitational field g has an associated magnetic-like field![]() . Hence, one can make the very bold conclusion that the very Laws of Nature (7 & 9) invariably imply an associated magnetic-like field for the gravitational field. Following tradition, we shall call this magnetic-like field the gravitomagnetic field and for short, we shall call it the g-magnetic field.
. Hence, one can make the very bold conclusion that the very Laws of Nature (7 & 9) invariably imply an associated magnetic-like field for the gravitational field. Following tradition, we shall call this magnetic-like field the gravitomagnetic field and for short, we shall call it the g-magnetic field.
Now, Equations (7) and (13) have a seductive and irresistible resemblance with Maxwell’s source coupled equations so much that for the brave that will set their mind on this, they most probably would proceed without detouring [2] to make a complete formal analogy with Maxwell’s equations. Under this scheme of a formal analogy, as a complete set, the gravitomagnetic equation is:
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
In Professor Behera [2] ’s derivation of the above set of four equations, Equations (15) and (18) have a just mathematical and physical existence, while Equations (16) and (17) not enjoy this same privilege. As stated above, these equations are argued into existence by Professor Behera [2] by way of analogy in pretty much the same way Professor Maxwell [1] and Dr. Heaviside [3] [4] speculated with no real ponderable justification. In our view―in Professor Behera [2] ’s thesis, one way to justify these equation’s existence would be to seek recourse to the work of Professor Jefimenko [5] and Hera [6] . If one did that, then, they would have to drop the whole approach to deriving Equations (15) and (18) via the Poisson-Laplace equation and the continuity equation.
We will demonstrate that Professor Hera [6] ’s method of deriving Equations (16) and (17) can be completed without the need to appeal to the methods of making an analogy nor making hand-waving arguments. For this, one starts by realizing that Equations (15) and (18) can be written in a more compact manner as:
![]() (19)
(19)
where, ![]() is a four momentum density, and the tensor field
is a four momentum density, and the tensor field ![]() (with the dimensions of per unit length squared) which is such that:
(with the dimensions of per unit length squared) which is such that:
![]() (20)
(20)
Equation (19) is not a new invention but a mathematically valid way if not an “economic”, efficient and elegant manner of writing Equations (15) and (18); we have not done anything new or strange here.
Now, the tensor field, ![]() , is antisymmetric, i.e.:
, is antisymmetric, i.e.:
![]() (21)
(21)
As is well known―or as can be shown or easily demonstrated is that, any smooth, differentiable and uniform continuous antisymmetric two-rank tensor field,![]() ; is that, it can be written as the curl of a smooth, differentiable and uniform continuous vector field,
; is that, it can be written as the curl of a smooth, differentiable and uniform continuous vector field, ![]() , i.e.:
, i.e.:
![]() (22)
(22)
where, ![]() , is the gravitomagnetic four vector potential and is here defined such that,
, is the gravitomagnetic four vector potential and is here defined such that, ![]() where the quantity
where the quantity ![]() has been inserted to be part of the magnetic vector potential,
has been inserted to be part of the magnetic vector potential, ![]() , so that all the components of the four vector potential,
, so that all the components of the four vector potential, ![]() , have the same dimensions.
, have the same dimensions.
Now, if, ![]() , is defined as it is defined in (22) and as-well,
, is defined as it is defined in (22) and as-well, ![]() , is also defined as it is defined in (20), then a comparision of the individual components of (20) and (22) invariably leads to the following definitions or identification:
, is also defined as it is defined in (20), then a comparision of the individual components of (20) and (22) invariably leads to the following definitions or identification:
![]() (23)
(23)
![]() (24)
(24)
where in (23),![]() . The reader should take note of the fact that,
. The reader should take note of the fact that, ![]() , is different from,
, is different from,![]() . Further, the reader should note that if,
. Further, the reader should note that if, ![]() , is defined as it is defined in (23), then, the vector,
, is defined as it is defined in (23), then, the vector, ![]() , will have to have the same dimensions as speed or velocity. These definitions (23) and (24) are all one needs in-order to deduce the field Equations (16) and (17). That is, by taking the curl on both-sides of Equation (23) one is led to Equation (16) and by taking the divergence on both-sides of Equation (24), one is led to Equation (17). In this way, we have without making any analogy or making any hand-waving arguments, demonstrated by way of appealing to ponderable mathematical facts, that Equations (16) and (17) have justifiable equations in the scheme of Professor Hera [2] ’s thesis of using the Poisson-Laplace equation and the continuity equation to demonstrate the implied existence of (15) and (18).
, will have to have the same dimensions as speed or velocity. These definitions (23) and (24) are all one needs in-order to deduce the field Equations (16) and (17). That is, by taking the curl on both-sides of Equation (23) one is led to Equation (16) and by taking the divergence on both-sides of Equation (24), one is led to Equation (17). In this way, we have without making any analogy or making any hand-waving arguments, demonstrated by way of appealing to ponderable mathematical facts, that Equations (16) and (17) have justifiable equations in the scheme of Professor Hera [2] ’s thesis of using the Poisson-Laplace equation and the continuity equation to demonstrate the implied existence of (15) and (18).
Another way to generate the field Equations (16) and (17) is to note that given the definitions (23) and (24), and the field tensor, ![]() , one can easily show that:
, one can easily show that:
![]() (25)
(25)
which is the Bianachi identity. From this equation, the field Equations (16) and (17) follow smoothly. So, effectively, the mass continuity equation together with the Poisson-Laplace equation for the gravitational field, are sufficient to demonstrate that gravitamagnetism is a just physical theory with a firm fundamental physical basis.
In his search for a causal theory of gravitation, Professor Einstein [16] [17] did at some point consider gravitomagnetism in the sense of a formal analogy of the gravitational phenomenon with Maxwell’s electrodynamics in much the same way Professor Maxwell [1] and Dr. Heaviside [3] did. However, this Professor Einstein did within the framework of his GTR as part of the first order approximation. So, GTR’s gravitomagnetism is not an exact physical phenomenon as the present. Professor Einstein sought a casual theory of gravitation i.e., a theory in which the gravitational phenomenon is transmitted at a finite speed, a speed less than or equal to the speed of light in vacuum. On this matter of casual theory of gravitation, before the 1913 Congress of Natural Scientists in Vienna―Austria; Professor Einstein made a notable critical remark [18] on Newtonian gravitation, he said of it:
“After the untenability of the theory of action at distance had thus been proved in the domain of Electrodynamics, confidence in the correctness of Newton’s action-at-a-distance theory of gravitation was shaken. One had to believe that Newton’s Law of Gravity could not embrace the phenomena of gravity in their entirety, any more than Coulomb’s Law of Electrostatics embraced the theory of electromagnetic processes.”
Certainly―as Professor Behera [2] contended; had Professor Einstein seen and studied more carefully Dr. Heaviside [3] [4] ’s field equations, and perhaps sought a non-speculative but a meaningful fundamental physical basis for their existence as has been sought herein and as-well by Professor Hera [6] , Behera [2] and Jefimenko [5] , surely, his critical remark on Newtonian gravitation would have been grossly different.
3. Gravitomagnetic Waves
Just as is the case with Electromagnetism, gravitomagnetic waves (hereafter, GM-Waves) are a clear prediction of not only the present gravitomagnetic theory―but all gravitomagnetic theories. In vacuum, we have:
![]() (26)
(26)
![]() (27)
(27)
As can clearly be read-off from (26) and (27), these GM-Waves travel in empty space at the speed![]() . Now, most if not all gravitomagnetic theories speculate the speed of GM-Waves must be the same as the speed of light in vacuum. We here are not going to speculate, but conclusively prove in Section 5 that
. Now, most if not all gravitomagnetic theories speculate the speed of GM-Waves must be the same as the speed of light in vacuum. We here are not going to speculate, but conclusively prove in Section 5 that ![]() is equal to the speed of light in vacuum, i.e.,
is equal to the speed of light in vacuum, i.e.,![]() . We expect these GM-Waves to have the same properties as electromagnetic waves.
. We expect these GM-Waves to have the same properties as electromagnetic waves.
An important question is “How are these GM-Waves generated and how are they to be detected?” The gravitational phenomenon, in both Newtonian and Einsteinian theories, is often assumed to be a central field phenomenon, i.e., the resulting field depends only on the radial distance from the source, the field is spherically symmetric. If we did assume this here, then, the gravitomagnetic vector field ![]() will also be a central field, i.e.,
will also be a central field, i.e.,![]() . If,
. If, ![]() , then,
, then,![]() . Once,
. Once, ![]() , then there would be no GM-Waves. If we are to have GM-Waves, we need to have,
, then there would be no GM-Waves. If we are to have GM-Waves, we need to have, ![]() , or,
, or,![]() .
.
So, asking “How are these GM-Waves generated?” amounts to asking how does one obtain the conditions, ![]() , or,
, or,![]() ? We have argued in [19] -[21] that for a spinning gravitational body that has one spin axis, the resulting gravitational field is not a central field,
? We have argued in [19] -[21] that for a spinning gravitational body that has one spin axis, the resulting gravitational field is not a central field, ![]() , but an axial-field phenomenon where,
, but an axial-field phenomenon where,![]() . Therefore, it follows that if our thesis is correct, then, GM-Waves will be generated by any spinning gravitational body. Therefore, there must exist a fully fledged particle that conveys the gravitomagnetic force in much the same way the photon does convey the electromagnetic force. For our purposes, let us call the photon equivalent of the gravitomagnetic force a gravitas particle1 and let us give it a symbol
. Therefore, it follows that if our thesis is correct, then, GM-Waves will be generated by any spinning gravitational body. Therefore, there must exist a fully fledged particle that conveys the gravitomagnetic force in much the same way the photon does convey the electromagnetic force. For our purposes, let us call the photon equivalent of the gravitomagnetic force a gravitas particle1 and let us give it a symbol![]() .
.
4. Massive Gravitomagnetic Photon
The proposed Unified Field Theory (UFT) [15] ―a theory upon which the present theory is ultimately based; requires that all particles including the photon must have a mass, this obviously includes the gravitas (i.e., the gravitomagnetic equivalent of the photon). Massive photons pause (at least) four problems, namely, they:
1) Lead to a violation of gauge invariance in Quantum Field Theories (QFT) [22] .
2) Lead to short range and short lived photons [22] [23] .
3) Lead to three extra degrees of freedom, which amongst many other things, this would lead to a modified Plank Radiation Law [22] .
4) Lead to an energy dependant speed of light [22] .
In the readings [24] [25] , we demonstrated that problems (1), (2) and (3) can be solved via the introduction of a special gauge condition, which for gravitomagnetism would be:
![]() (28)
(28)
Of massive photons, the only problem that remains unsolved by (28) is that the speed of light becomes energy dependent. But this is not necessarily a problem as has been argued in [24] , that this is a welcome solution on explaining the ponderous observations of the time delay in the arrival times of gamma rays of different energies from Gamma-Ray Burst events. The special gauge condition (28), requires us to drop the traditional Lorenz gauge2 ![]() [26] and adopt the modified Lorenz gauge [15] [25] :
[26] and adopt the modified Lorenz gauge [15] [25] :
![]() (29)
(29)
where![]() .
.
Equation (19) is the equation for a massless gravitas. For a massive gravitas, as derived in [15] , we will have to add the gravitomagnetic Proca term as follows:
![]() (30)
(30)
If the work presented in [15] is correct, then, QFT of Gravity can be build along the same lines as Quantum Electrodynamic Theories QED. As with QED theories, the gauge conditions (28) and (29) will lead to theories that do not (1) violate gauge invariance, (2) lead to short range and short lived gravitas, (3) lead to a gravitas with three and not six degrees of freedom.
![]()
2We must note that the Lorenz gauge, ![]() , is a condicio sine qua non for the conservation
, is a condicio sine qua non for the conservation![]() , of the current,
, of the current,![]() .
.
In (30), the field tensor ![]() has dimensions of per unit length squared because
has dimensions of per unit length squared because ![]() is a dimensionless quantity and as usual
is a dimensionless quantity and as usual ![]() has the dimension of per unit length. The four momentum density
has the dimension of per unit length. The four momentum density ![]() is such that
is such that![]() . Notice that we have written the four momentum density as
. Notice that we have written the four momentum density as ![]() and not as
and not as ![]() and the reason for this is that for all gravitomagnetic field quantities where we need―for dimensional consistency; to insert a fundamental physical constant with the dimensions of length per unit time, we here insert the quantity
and the reason for this is that for all gravitomagnetic field quantities where we need―for dimensional consistency; to insert a fundamental physical constant with the dimensions of length per unit time, we here insert the quantity![]() , which is the speed of gravitomagnetic waves. Traditionally in physics we can insert the speed of light c. The problem with this approach here is that this will automatically lead us to the conclusion that gravitomagnetic waves propagate at the speed of light c. We want this fact to emerge from the theory in a natural manner. It will be seen in the succeeding section that, having here not made the prior assumption that
, which is the speed of gravitomagnetic waves. Traditionally in physics we can insert the speed of light c. The problem with this approach here is that this will automatically lead us to the conclusion that gravitomagnetic waves propagate at the speed of light c. We want this fact to emerge from the theory in a natural manner. It will be seen in the succeeding section that, having here not made the prior assumption that![]() , this fact finally emerges naturally from the theory. The speed of light c here enters the gravitomagnetic fold via the derivatives
, this fact finally emerges naturally from the theory. The speed of light c here enters the gravitomagnetic fold via the derivatives ![]() and our task is to show that the internal logic leads to the fact
and our task is to show that the internal logic leads to the fact![]() .
.
5. Speed of Gravitomagnetic Waves
According to the foregoing, the speed of gravity or the speed of the resulting gravitational waves is![]() . It has long been speculated but never proved either in theory, observation or in any experiment, that the gravitational phenomenon is transited at the same speed of light c. Shortly, we will unequivocally and conclusively demonstrate that the gravitomagnetic theory as presented herein implies that the speed of gravity is the same as that for light. We will start from the massive gravitomagnetic field Equation (30) and apply to it the special gauge condition (28) and as-well the modified Lorenz gauge (29), where upon one is led to (see [15] [25] ):
. It has long been speculated but never proved either in theory, observation or in any experiment, that the gravitational phenomenon is transited at the same speed of light c. Shortly, we will unequivocally and conclusively demonstrate that the gravitomagnetic theory as presented herein implies that the speed of gravity is the same as that for light. We will start from the massive gravitomagnetic field Equation (30) and apply to it the special gauge condition (28) and as-well the modified Lorenz gauge (29), where upon one is led to (see [15] [25] ):
![]() (31)
(31)
The mass term in (30) vanishes because of the gauge conditions (28) and (29). The 0-component of (31) is:
![]() (32)
(32)
and the space component of this same equation is:
![]() (33)
(33)
Equation (32) has been considered in [27] as an equation describing a dynamic gravitational field. It is has been shown therein that, one can derive five gravitational potentials (![]() ). Under the present gravitomagentic scheme, these five gravitational potentials will have corresponding gravitomagnetic vector potentials (
). Under the present gravitomagentic scheme, these five gravitational potentials will have corresponding gravitomagnetic vector potentials (![]() ). These potentials
). These potentials ![]() have been hypothesised (in [27] ) to operate concurrently on all gravitating systems.
have been hypothesised (in [27] ) to operate concurrently on all gravitating systems.
Now, if we assume a non-static gravitational field, then, the gauge condition (29), becomes:
![]() (34)
(34)
then, from the above equation, it follows that:
![]() (35)
(35)
The above equation is easily deducible from Equation (34). Now, applying the operator, ![]() , on both-sides of (36), we will have:
, on both-sides of (36), we will have:
![]() (36)
(36)
From (32), it follows that the above reduces to:
![]() (37)
(37)
Since![]() , it follows that (37) will reduce to:
, it follows that (37) will reduce to:
![]() (38)
(38)
Comparing the left hand-side of (38) and (33), i.e., ![]() , we will have,
, we will have, ![]() and this implies
and this implies![]() ; given Equation (14), this equation,
; given Equation (14), this equation, ![]() , implies that:
, implies that:
![]() (39)
(39)
Therefore, the speed of GM-Waves is the same as that for light in a vacuum. In our feeble view, this is an important result as it emerges from within the internal structure and logic of the theory, it is not imposed from outside as is the case in most gravitomagnetic theories, were it is ad hocly or impromptu assumed that the speed of gravitomagnetic waves or gravitational waves must be the same as that for light. From the result (14) and (39), it follows that the fundamental constant, ![]() is known, i.e.:
is known, i.e.:
![]() (40)
(40)
In the next section, by deriving the corresponding Lorentz term, we shall now apply the present gravitomagnetic theory to see what it “has to say” insofar as known gravitational anomalies is concerned.
6. Gravitomagnetic Lorentz Force
What is the equivalent Gravitomagenetic Lorentz (hereafter GM-Lorentz) equation of motion? We know that the Electromagnetic Lorentz (hereafter EM-Lorentz) equation of motion is given by![]() , where q is the electronic charge of a particle moving with speed velocity, v, inside an electric and e-magnetic field, E, and,
, where q is the electronic charge of a particle moving with speed velocity, v, inside an electric and e-magnetic field, E, and, ![]() , respectively. Like,
, respectively. Like, ![]() , as given in (23),
, as given in (23), ![]() , where
, where ![]() is the electric potential and
is the electric potential and ![]() is the electric magnetic potential. Literally most if not all researchers (cf. [28] -[32] ) in the field of gravitomagnetism have proceeded to make the formal analogy,
is the electric magnetic potential. Literally most if not all researchers (cf. [28] -[32] ) in the field of gravitomagnetism have proceeded to make the formal analogy, ![]() , for the GM-Lorentz force
, for the GM-Lorentz force
field, whereafter they have proceeded to investigate the Lorentz term, ![]() , to try and explain gravitational
, to try and explain gravitational
anomalies. In the equation, ![]() , the quantity,
, the quantity, ![]() , is the gravitational charge or the gravitational mass of the test body inside the GM-Lorentz field.
, is the gravitational charge or the gravitational mass of the test body inside the GM-Lorentz field.
While there are a number of ways to arrive at the Electromagnetic Lorentz Force Law (cf. [33] ), it can be shown that amongst these numbers of ways, this law can be obtained from Maxwell’s equations on the assumptions of the Coulomb gauge ![]() provided one assumes that the electric portion of the force acted on a charge is known, and the magnetic component is perpendicular to the velocity of motion of the charged particle [34] . This means that making a complete formal analogue assumes for the GEM, the gravitomagneto Coloumb gauge
provided one assumes that the electric portion of the force acted on a charge is known, and the magnetic component is perpendicular to the velocity of motion of the charged particle [34] . This means that making a complete formal analogue assumes for the GEM, the gravitomagneto Coloumb gauge![]() , which in itself implies a static gravitational field provided the Lorenz gauge
, which in itself implies a static gravitational field provided the Lorenz gauge ![]() is assumed.
is assumed.
As part of our contribution in the present work, we depart from this tradition of assuming that the GM- Lorentz field is given by,![]() . We will stick to the internal logic of the theory in which process we (perhaps) demonstrate that researchers who have assumed the GM-Lorentz field,
. We will stick to the internal logic of the theory in which process we (perhaps) demonstrate that researchers who have assumed the GM-Lorentz field, ![]() , may probably not have been correct in doing so. The Lorentz term,
, may probably not have been correct in doing so. The Lorentz term, ![]() , emerges as a result of the Coulomb gauge,
, emerges as a result of the Coulomb gauge, ![]() , where
, where ![]() is the e-magnetic vector potential. Maxwell’s EM-theory obeys the Lorenz gauge,
is the e-magnetic vector potential. Maxwell’s EM-theory obeys the Lorenz gauge,
![]() . By assuming that,
. By assuming that, ![]() , we are asserting that
, we are asserting that![]() . That is, the Coulomb gauge,
. That is, the Coulomb gauge,
![]() , implies a static electric potential.
, implies a static electric potential.
This Coulomb gauge, ![]() , further implies that the e-magnetic vector potential,
, further implies that the e-magnetic vector potential, ![]() , and the electric potential,
, and the electric potential, ![]() are independent of each other, so much that one is free to choose is vector,
are independent of each other, so much that one is free to choose is vector,![]() . The choice that has been made is one that allows one to make this vector a function of the vector r and the e-magnetic field,
. The choice that has been made is one that allows one to make this vector a function of the vector r and the e-magnetic field, ![]() , i.e.,
, i.e.,![]() . If,
. If, ![]() , then,
, then, ![]() , hence the EM-Lorentz force,
, hence the EM-Lorentz force,![]() . From these arguments, it is crystal clear that the Lorentz term,
. From these arguments, it is crystal clear that the Lorentz term, ![]() , is a result of the freedom afforded to us by the Coulomb gauge,
, is a result of the freedom afforded to us by the Coulomb gauge,![]() .
.
Now, just as the EM-Lorentz force field is given by, ![]() , the GM-Lorentz force field,
, the GM-Lorentz force field, ![]() , which when written in full is:
, which when written in full is:
![]() (41)
(41)
where the term, ![]() , is the normal Newtonian. This new term, is at best, termed the dark-force,
, is the normal Newtonian. This new term, is at best, termed the dark-force, ![]() , i.e.:
, i.e.:
![]() (42)
(42)
If this dark-force really exists, it may explain some of the observed gravitational anomalies that have puzzled a great number of scientists today. It is a term which if real, then, it will―depending on its strength; certainly lead to significant anomalous gravitational effects that are not modelled in the term,![]() .
.
Since we have shown in [27] that (31) has five solutions for the gravitational potential ![]() and each of these five solutions have an associated magnetic
and each of these five solutions have an associated magnetic![]() , it follows that when writen in full (44) is given by:
, it follows that when writen in full (44) is given by:
![]() (43)
(43)
Since ![]() is given in (35), it follows that the above equation can further be written as:
is given in (35), it follows that the above equation can further be written as:
![]() (44)
(44)
where![]() ,
, ![]() or
or ![]() is a set of three fundamental parameters with the dimensions of per unit length and these parameters do not dependent explicitly on either the space
is a set of three fundamental parameters with the dimensions of per unit length and these parameters do not dependent explicitly on either the space ![]() or time
or time ![]() coordinates. As preliminarily suggested in the reading [27] , the four new potentials (
coordinates. As preliminarily suggested in the reading [27] , the four new potentials (![]() ; as defined there [27] ) hold the potential to solve a number of astrophysical problems, namely:
; as defined there [27] ) hold the potential to solve a number of astrophysical problems, namely:
1) The Problem of the Flat Rotation Curves of Spiral Galaxies [35] -[39] which is popularly known as the Darkmatter Problem.
2) The Flyby Anomalies Problem [40] [41] .
3) The Pioneer Anomaly Problem (cf. [42] [43] ).
4) The Origins of the Titius-Bode Law (cf. [44] -[46] ) and Planetary Rings Systems.
5) The Origins of the Tilt About the Ecliptic Plane of Planetary Orbits. Not much thought has been given into the enquiry of why planetary orbits are tilted or whether one can find a systematic pattern in this. If our work is correct, it somehow suggests a possible pattern that can clearly be deciphered.
6) The Secular Increase in the Mean Sun-(Earth-Moon) Distance [47] -[50] and the Mean Moon-Earth Distance [51] [52] .
Clearly, there is a plethora of work ahead. All we can say about this work, is that―most of it has been conducted, all it awaits is finalization, where upon it will be submitted for publication. This work, together with [15] , only set the stage for the said explorations.
7. General Discussion
From the Hera Existence Theorem [6] and other lines of thought, we have argued that gravitomagnetism is a fully fledged and independent field in much the same way electromagnetism is. A hallmark of gravitomagnetism as here laid down is that it opens up the possibility of a time variable gravitationl G. Since it was first proposed in the 1930’s by Professor Dirac and Milne [53] [54] , that is, the idea of time variable-G, there has never been a solid theoretical foundation to furnish this hypothesis. While the possibility of a time viarable-G is here opened up, we have, via the Lorenz gauge constraint to be a fundamental natural constant that does not vary with time. Apart from the traditional Newtonial gravitation force (component), as demonstrated in [27] , the emergent four Poisson-Laplace equation for gravitation from the present gravitomagnetic theory naturally leads to four new gravitational components. The existence of the said four Poisson-Laplace equation is justified by the present gravitomagnetic theory.
With regard to a time variable Newtonian gravitational constant G, recent research [55] has shown that, at least for the last 9 billion of the Universe’s assumed 13.8-billion-year history, the gravitational constant has not varied more than (at most) one part in a billion. This result is obtained after an exhaustive study of about 580 observed supernovae events by Professor Jeremy Mould and his Ph.D. student Syed Uddin at the Swinburne Centre for Astrophysics and Supercomputing and the ARC Centre of Excellence for All-Sky Astrophysics. While this research gives impetus to the present theory which assumes![]() , it does not mean that the gravitational constant does not have a time dependence. Just as in the case of the mass of the photon, it would be much more difficult to prove experimentally that indeed
, it does not mean that the gravitational constant does not have a time dependence. Just as in the case of the mass of the photon, it would be much more difficult to prove experimentally that indeed![]() , than to prove otherwise.
, than to prove otherwise.
On one the achievements of the present theory, we can safely say that, an important outcome of the present theory is that we have shown that gravitomagnetic waves must―as electromagnetic waves do; travel at the speed of light and these most certainly are generated by spinning concentrations of gravitating mass. In the theory, we make no prior assumption to this fact but set the speed of these waves to ![]() and using only the internal logic of the theory, we show that
and using only the internal logic of the theory, we show that![]() . This is very much unlike in most if not all gravitomagnetic theories where this fact is deduced as part and parcel of the package of making a formal analogy with Maxwellian electrodynamics.
. This is very much unlike in most if not all gravitomagnetic theories where this fact is deduced as part and parcel of the package of making a formal analogy with Maxwellian electrodynamics.
Another aspect that sets the present gravitomagnetic theory apart from most if not all gravitomagnetic theories in existence today (cf. [28] -[32] ) is that, for the equivalent Lorentz equation of motion, we departed from making a complete formal analogy, in which event we have not adopted the Lorentz force term![]() . We have used the Lorentz gauge to deduce the gravitomagnetic vector potential and because of this, it the present gravitomagnetic vector potential depends on the gravitational potental
. We have used the Lorentz gauge to deduce the gravitomagnetic vector potential and because of this, it the present gravitomagnetic vector potential depends on the gravitational potental![]() . Consequently, the the present gravitomagnetic theory depends on just one parameter, namely, the gravitational potential
. Consequently, the the present gravitomagnetic theory depends on just one parameter, namely, the gravitational potential![]() . This kind of simplification is desired by Occam’s Razor which forbids the use of multiple parameters when one can do with less.
. This kind of simplification is desired by Occam’s Razor which forbids the use of multiple parameters when one can do with less.
Despite the fact that we have tried to distance the present gravitomagnetic theory from our proposed UFT [15] , it is very much a part of it. What we have done is basically argue from the independent view-points of Professor [6] and Behera [2] . Professor [2] justifies the from a physical standpoint, the existence of a four gravitomagnetic vector potential, while Professor [6] , uses only the equation of conversation of mass to justify the existence of a four gravitomagnetic vector potential. We feel that the same approach that has been used to formulate QED, this same approach can be used to find a Quantum Theory of Gravity in the framework of gravitomagnetism.
In-closing, allow us to say that the main purpose of this work has been to justify the fundamental physical basis of gravitomagnetism well outside the framework of our proposed UFT [15] . In the UFT [15] , gravitation is introduced by the sleight of hand and not naturally. So, we found it difficult to justify its existence from the confines of the UFT [15] and only realise that the only way was to justify is via Hera Existence Theorem [6] through the equation of mass. The resulting equations have―amongst others; the potential to solve the problem of the flat rotation curves of spiral galaxies [35] -[39] , the flyby anomalies [40] [41] , the Pioneer anomaly (cf. [42] [43] ), the origins of the Titius-Bode Law (cf. [44] -[46] ), the existence planetary rings systems, the origins of the tilt about the ecliptic plane of planetary orbits, the secular increase in the mean Sun-(Earth-Moon) distance [47] -[50] and the mean Moon-Earth distance [51] [52] . This clearly points to the plethora of work to be done ahead. Given the ground that we have cover on that front, we are very hopeful that the said future is going to give gravitomagnetism impetus, whereby it will be given a fundamental and independent existence as a fully fledged physical theory.
8. Conclusions
Assuming the acceptability of the ideas here presented, we hereby make the following conclusion:
1) Gravitomagnetism is a valid physical phenomenon since it can be justified from well accepted fundamental physics principles.
2) Gravitomagnetic waves travel at the speed of light c.
3) As pointed herein, gravitational anomalies such as darkmatter, the secular recession of planets from the Sun, the Pioneer anomaly etc., may prove to be effects caused by the gravitomagnetic field.
NOTES
1The term graviton cannot be used here because it already means a hypothetical tensor particle that conveys the force of gravity. The term gravitas is the term first coined by the great Sir Isaac Newton when he was referring to what we now call gravity.