1. Introduction
In an earlier study [1] , we calculated the intrinsic quantum flux of a photon through the intrinsic quantum flux of the gamma photons created as a result of the electron-positron (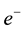
-
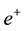) annihilation. By using the flux conservation rule, which is an element of the conservation of the canonical angular momentum, we find that each gamma photon carries a magnetic flux quantum of 
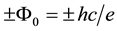with itself along the propagation direction. Here, the (+) and (−) signs stand for the right and left hand circular helicity respectively. The aim of the present work is to calculate the magnetic moment of any photon through the magnetic moment of a gamma photon and to find a unique relation between the intrinsic fluxes and the magnetic moments of electron, positron and photon.
The first experiment about the magnetic moment of a photon was done in 1896 by Zeeman [2] , who discovered the spectral lines from sodium. When it was put in a flame, the light emitted was split up into several components in a strong magnetic field. A long period after Zeeman, experimental attempts about photon’s magnetic moment through the Stern-Gerlach experiment (SGE) with photons have started recently by Karpa et al. [3] - [5] .
SGE was devised in 1922 to show that electron had a non-zero magnetic moment [6] and later it was also extended to the nuclei [7] . In general, in the SGE the magnetic field gradient serves as a detector for the particle’s magnetic moment vector: If the magnetic field is a non-uniform field along the z direction such as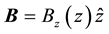
, then because of the torque 
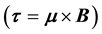on the particles, the magnetic moment vector can have z-component only: 
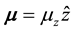(where 
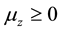or
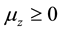). On the other hand, the potential energy 
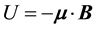produces a force
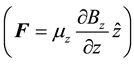which has quantized values as
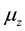. Depending on whether (
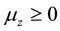or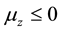
), the particles
are deflected upward or downward. In the SGE with electron, the electron beam is deflected into two sub-
beams which means that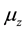 
takes only two possible quantized values which are equal to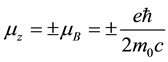 
where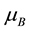 
is called the Bohr magneton. Because of the negative charge of the electron, the relation between spin and the magnetic moment is set as ![]()
where g is the Lande-g factor which is equal to 2 and ![]()
is the spin angular momentum vector. So in the SGE with electron, the z component of spin ![]()
takes
only two possible values which are:![]()
. Therefore if ![]()
then the spin-down electrons will be def-
lected upward while the spin-up ones will be deflected downward. Similarly if we have SGE with a positron beam, because of the positive charge, the spin-down positrons will be deflected downward while the spin-up ones will be deflected upward. But when it comes to the gamma photons, which are the composite particles made up of an electron and a positron, the direction of the deflection is determined by the sign of the![]()
. Therefore, the magnetic moment of the gamma photon is an important property and it needs to be calculated in detail. We have calculated the magnetic moment of a photon through the magnetic moment of a gamma photon and found that the z-component of the magnetic moment is equal to ![]()
where ![]()
is the angular frequency of photon. Here, the (+) and (−) signs correspond to the right and left hand circular helicity respectively.
We have also found a unique relation between the intrinsic fluxes and the magnetic moments of the particles such as electron, positron and the photon. We show that for all these three particles the unique relation between the intrinsic fluxes and the magnetic moments is given by:![]()
.
We argue that any photon propagating in z direction with an angular frequency ![]()
will have a non-zero magnetic moment of ![]()
depending on the helicity. Since the intrinsic flux of a general photon is![]()
; then for a general photon the relation between the intrinsic flux and the magnetic moment will be ![]()
as well.
Because of the two symmetric values of the magnetic moment of a photon, we expect a splitting (deflection) of the beam into two symmetric subbeams in a Stern-Gerlach experiment. We also expect that the splitting will be more prominent for lower energies. We believe that the present work will help to understand the Stern-Gerlach experiment of photons [3] -[5] in detail. In the theoretical side, the present work will bring a new insight to quantum mechanics as well.
Electron-positron (![]()
-![]()
) annihilation process has been known for almost about 75 years [8] -[16] . After the collision, we have two gamma photons with the same energy but with different helicities. In this collision, we have the conservation of charge, energy, linear momentum and the conservation of the canonical angular momentum which requires the conservation of the total quantum flux and the total magnetic moments. Magnetic flux quantization has been known for more than 60 years [17] [18] . Saglam and Boyacioglu [19] , with a semiclassical method, calculated quantized magnetic fluxes through the Landau orbits of an electron including the effect of the spinning motion. They show that the spin contribution to the quantized magnetic flux is equal to
![]()
depending on the spin orientation. Here,![]()
. Recently, Wan and Saglam
[20] calculated the intrinsic magnetic flux of an electron due to its orbital motion in a non-relativistic hydrogen atom by using the Schrödinger equation and then extended their result to incorporate the spin angular momentum as well.
Most recently Saglam and Sahin [1] calculated the intrinsic quantum fluxes of a free electron and free positron by a semi classical model in the absence of an external magnetic field. As the subject of present study is related to the intrinsic fluxes of ![]()
and ![]()
these fluxes must be calculated in the frame of the relativistic quantum mechanics as well. Since the above mentioned calculations use the non-relativistic Schrödinger equation, a rigorous proof has been needed also. In Appendix I, we calculate the intrinsic fluxes of ![]()
and ![]()
by the spin dependent solutions [21] of the Dirac equation for a free electron (or positron) in a uniform magnetic
field. We then prove that the intrinsic fluxes of ![]()
and ![]()
are ![]()
which agree with the previous
calculations [19] [20] .
In Appendix II, we introduce the conservation of the quantum flux in collisions: We write the Lagrangian of an electron moving in a uniform magnetic field in z direction then calculate the z-component of the conserved canonical angular momentum Jc which has two elements: The conservation of the kinetic angular momentum and the conservation of the magnetic flux. Therefore in the electron-positron annihilation, the conservation of the canonical angular momentum requires both conservation of the spin angular momentum and the conservation of the quantum flux which is originated from the intrinsic fluxes of ![]()
and![]()
. We also show that the conservation of the quantum flux can be replaced by the conservation of the magnetic moments as well.
The outline of this paper is as follows: In Section 2, we derive the relation between the intrinsic fluxes and the magnetic moments of electron and positron. In Section 3, we calculate the magnetic moment of photon. In Section 4, we give the conclusions.
2. The Relation between the Intrinsic Fluxes and the Magnetic Moments of an Electron and Positron
The definition of the spin magnetic moment vector ![]()
for a free electron ![]()
and a positron ![]()
are:
![]()
(1a)
![]()
(1b)
Here, g is the Lande-g factor which is equal to 2 for both particles and ![]()
is the spin angular momentum. De- pending on the spin orientation, the z-components of the magnetic moments for spin-up and down electron are:
![]()
(2a)
![]()
(2b)
Similarly the related z-components of the magnetic moments for spin-up and down positron are:
![]()
(3a)
![]()
(3b)
where ![]()
is the rest mass of the electron and ![]()
is the Bohr magneton.
In Appendix I, we calculate the intrinsic fluxes of ![]()
and ![]()
by the spin dependent solutions [21] of the Dirac equation for a free electron (or positron) in a uniform magnetic field. We then prove that the intrinsic fluxes for spin-up and down electron are:
![]()
(4a)
![]()
(4b)
respectively. Similarly the intrinsic fluxes for spin-up and down positron are:
![]()
(5a)
![]()
(5b)
If we compare the z-components of the magnetic moments and the spin dependent fluxes for both electron and positron Equations (2a)-(5b) we write the relation between the intrinsic flux and the magnetic moment of both electron and positron.
![]()
(6)
3. Calculation of the Magnetic Moment of a Photon
To calculate the magnetic moment of a photon, our starting point will be the electron-positron annihilation process ending with the creation of two gamma photons with right and left hand circular helicities. After the collision we will have two photons with the same energy ![]()
but with different helicities. Just before the collision the relative spin orientation of ![]()
and ![]()
will be controlled by the Heisenberg exchange Hamiltonian [22] .
![]()
(7)
where![]()
, ![]()
are the spin vectors and J is the exchange integral. If we had two electrons instead, the exchange energy together with the Pauli exclusion principle requires that the spins of the electrons must be antiparallel. But for colliding (![]()
,![]()
) system, the minimum energy is obtained for parallel spins. Therefore just before the collision the total z-component of the spin of the colliding (![]()
,![]()
) system will be![]()
. That means there are two possibilities:
a) The electron is in spin-down state and the positron is in spin-down state.
b) The electron is in spin-up state and the positron is in spin-up state.
In Dirac notation, the states (a) and (b) can be defined as:
![]()
(8a)
![]()
(8b)
which build an orthonormalized set. Namely
![]()
(8c)
![]()
(8d)
![]()
(8e)
![]()
( 8f )
where ![]()
and ![]()
are the volume elements for electron and positron respectively.
The expectation values of the total z-components of the spin ![]()
for the eigenstates (a) and (b) given in Equation (8a), (8b) are:
![]()
(9a)
![]()
(9b)
where ![]()
and ![]()
are the spins of electron and positron respectively.
Since the states (a) and (b) are equally probable, the total wave function ![]()
before the collision will be given by:
![]()
(10)
which is the quantum entanglement of the states![]()
, ![]()
, ![]()
and![]()
.
The expectation value of ![]()
for the initial state ![]()
in Equation (10) is:
![]()
(11)
where we used Equations (9a), (9b).
The total wave function, ![]()
of the system after the collision, will correspond to another entanglement of the states![]()
, ![]()
, ![]()
and ![]()
provided that the total z-component of the spin of the final state is again zero. The only possible entanglement that results in zero spin is given by:
![]()
(12)
This corresponds to two different gamma photons created with opposite circular helicities [1] . The eigenstates corresponding to the right hand and left circular helicities are:
![]()
(13a)
![]()
(13b)
respectively.
As we calculated in Equations (9a), (9b), the expectation values of the total z-components of the spin ![]()
for the eigenstates ![]()
and ![]()
of Equation (13) are:
![]()
(14a)
![]()
(14b)
The expectation value of ![]()
for the final state ![]()
in Equation (12) is:
![]()
(15)
where we used Equations (14a) and (14b).
If we compare the expectation value of ![]()
before and after the collision [Equation (11) and Equation (15)], we see that the conservation of the spin angular momentum is fulfilled. However, in Appendix II we show that the conservation of the canonical angular momentum requires also the conservation of the flux quantum or the magnetic moments as well (because of the relation given in Equation (6) the conservation of the flux quantum will be equivalent to the conservation of the magnetic moments).
Now using the Equations (2a)-(3b) we can calculate the expectation values of the z-components of the magnetic moment vectors for the eigenstates![]()
, ![]()
, ![]()
and ![]()
[given in Equations (8a), (8b) and Equations (13a), (13b)]:
![]()
(16a)
![]()
(16b)
![]()
(16c)
![]()
(16d)
Next, using the Equations (16a)-(16d) we can calculate the expectation value of ![]()
(the total z-compo- nent of the magnetic moment) for the initial and the final states given in Equations (10), (12):
![]()
(17a)
![]()
(17b)
If we compare the expectation value of ![]()
for the initial state and the final state Equations (17a), (17b), we see that conservation of the total magnetic moment is also fulfilled. Therefore, the electron-positron annihilation resulting with the creation of two gamma photons simply corresponds to the transition from the initial entangled state ![]()
given by Equation (10) to the final entangled state ![]()
given by Equation (12).
As we stated above, the final state wave function given in Equation (12) corresponds to two different gamma photons created with opposite circular helicities after the collision. Because the eigenstate ![]()
corresponds to the gamma photon with the right hand circular helicity and the second eigenstate ![]()
corresponds to the gamma photon with the left hand one.
From the Equations (16c) and (16d), the z-component of the magnetic moment of the eigenstates, ![]()
and ![]()
(the gamma photons with the right hand (rh) and the left hand (lh) circular helicity) are:
![]()
(18)
![]()
(19)
respectively.
Now substituting the relation ![]()
in Equations (18), (19), we can write magnetic moments of the gamma photons in terms of the angular frequency,![]()
:
![]()
(20)
![]()
(21)
which must be true for any photon also. Namely a photon propagating in z direction with an angular frequency ![]()
carries a magnetic moment of mz = ± (ec/w) along the propagation direction. Here, the (+) and (−) signs stand for the right hand and left circular helicity respectively.
4. Conclusions
We have calculated the intrinsic magnetic moment of a photon through the intrinsic magnetic moment of a gamma photon created as a result of the electron-positron annihilation with the angular frequency w. We show that a photon propagating in z direction with an angular frequency ![]()
carries a magnetic moment of mz = ± (ec/w) along the propagation direction. Here, the (+) and (−) signs stand for the right hand and left circular helicity respectively. We have also found a unique relation between the intrinsic fluxes and the magnetic moments of the particles such as electron, positron and the photon as well. We show that for all these three particles the unique relation between the intrinsic fluxes and the magnetic moments is given by:![]()
.
Since for a photon mz is inversely proportional to the angular frequency w, a lower frequency implies a higher magnetic moment. Therefore in the first experiment done by Zeeman [2] in 1896, yellow light of sodium which was in the low frequency range of the optical spectrum was a right choice for that purpose. On the other hand although we used gamma photons to calculate the magnetic moment of a photon, we believed that a Stern-Gerlach experiment (SGE) with gamma photons was almost impossible as we had an extremely high frequency. Because of these two symmetric values of the magnetic moment, we expect a splitting of the photon beam in two symmetric subbeams in a Stern-Gerlach experiment. The splitting is expected to be more prominent for low energy photons. We believe that the present result will be helpful for understanding of the Stern-Gerlach experiment with photons [3] -[5] and also the behavior of the dark polaritons and the atomic spinor polaritons which is useful for the storage of the photonic qubits in a single atomic ensemble. A more complete work will be presented in the future.
Acknowledgements
The authors express their thanks to Professor Mesude Saglam for her encouragement and for her invaluable help.
Appendix I: Calculation of the Intrinsic Quantum Fluxes of Electron and Positron by Dirac Equation
Solution of Dirac Equation for a free electron moving in a homogeneous magnetic field was given by Saglam et al. [21] :
![]()
(AI-1)
![]()
(AI-2)
To calculate the intrinsic quantum flux of a relativistic free electron in a uniform magnetic field within the framework of Dirac theory, we shall follow a similar way that we followed earlier [20] : Namely, we shall first calculate the quantum flux through the probability current (particle current) density associated with the wave function of a free Dirac electron in a uniform magnetic field, then connect it to the flux element ![]()
by the self-inductance Le. The probability of electric current density for the circular motion along the ![]()
direction is given by:
![]()
(AI-3)
Assuming that electron is moving in ![]()
plane, we then write the surface current element coming from the circular ring of radius ![]()
and the thickness![]()
:
![]()
(AI-4)
Our next objective is to establish a quantized magnetic flux coming from the above current. A current element circulating around z-axis in a circle of radius ![]()
should enclose an induced magnetic flux element ![]()
which is proportional to the current given by Equation (AI-4):
![]()
(AI-5)
where ![]()
is the self-inductance [20] given by:
![]()
(AI-6)
Substitution of Equations (AI-3) and (AI-6) into Equation (AI-5) gives the total induced quantized magnetic flux:
![]()
. (AI-7)
To calculate the total induced quantized magnetic fluxes for spin-up and spin-down electrons, we substitute the wave functions of ![]()
and ![]()
states separately from Equation (AI-1) and Equation (AI-2) in Equation (AI-7): the spin dependent induced fluxes take the forms:
![]()
(AI-8a)
![]()
(AI-8b)
In Equations (AI-8a) and (AI-8b), the spin dependent intrinsic fluxes correspond to m = 0, which are![]()
. If we solve the Dirac equation for a free positron we simply replace (−e) with (e). Then the corresponding fluxes would be![]()
. So the intrinsic fluxes that electron and positron possess are:
![]()
(AI-9a)
![]()
(AI-9b)
![]()
(AI-9c)
![]()
. (AI-9d)
Appendix II: Conservation of the Canonical Angular Momentum in Terms of the Quantum Flux and the Magnetic Moment
The Lagrangian of an electron with mass ![]()
and electric charge (−e) moving in a uniform magnetic field in z direction ![]()
is given by, ![]()
, where ![]()
is the position vector in two dimensions, ![]()
is the velocity and ![]()
is the vector potential. The quantum flux in terms of radius and the magnetic field can be written as
![]()
(AII-1)
For an electron moving in the x-y plane in the counter clockwise direction with the angular frequency
![]()
, we get![]()
, where the time integral has been taken over one cyclic period![]()
.
The vector potential, ![]()
is now related to the magnetic flux ![]()
by
![]()
(AII-2)
The z-component of the conserved canonical angular momentum Jc is given by
![]()
(AII-3)
where J is the gauge invariant kinetic angular momentum of the electron.
Now using the relation in Equation (6):
![]()
(6)
We can write the conserved canonical angular momentum Jc in terms of the magnetic moment. Substitution of Equation (6) into (AII-3) gives:
![]()
(AII-4)
Here, Equations (AII-3) and (AII-4) simply state that the conservation of the canonical angular momentum requires also the conservation of the magnetic flux and the magnetic moment as well. In passing, we note that although the above calculations are carried out for an electron, the statement about the conservation of the magnetic flux and the magnetic moment will be valid for a positron as well. The only difference is that, for a positron the (−) signs in Equations (AII-3) and (AII-4) are replaced with the (+) signs.