Numerical Approximation of Quantum-Integrals Using the Appropriate Nodes and Weights ()
1. Introduction
Recently, much attention has been paid on q-calculus, especially on q-fractional calculus which finally most of them have changed to q-integral not easy and even possible to be solved analytically [1] . Although some series expansions have been developed for quantum integrals [2] and quantum differential equations and quantum difference equations [3] - [6] or q-fractional calculus [6] [7] , but because of small fractional power in the series expansion, one will expect a high degree of error in the truncated series [7] - [9] . The nominal numerical methods for approximating integrals do not seem to be appropriate for q-integrals. We could find less works for developing numerical procedures for accurate numerical solutions [9] - [14] . In this paper, we present a procedure for the numerical q-calculation of the q-integrals based on appropriate nodes and weights which are determined such that the error of q-integration is minimized. This study is organized such that in Section 2 we introduce the basic definitions and theorems related to the q-integrals; in Section 3, the main algorithm for the numerical approximation based on appropriate nodes and weights is introduced and the system of linear equations for the nodes and also nonlinear equations for the weights are established; in Section 4, numerical examples for illustration of the procedure are shown; finally, the related tables and graphs and conclusion are given.
2. Basic Definitions and Theorems
In this section we define the basic definitions and theorems related to the quantum integration
Jackson’s definition [15] for the q-integral is:
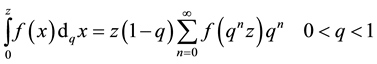 (1)
(1)
when 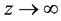
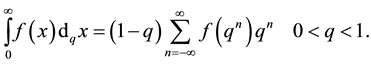 (2)
(2)
For the continuous function f in the interval [0, z] we have [8] :
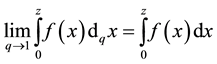 (3)
(3)
and
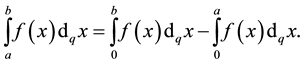 (4)
(4)
The generalized q-integral for 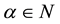 is defined as:
is defined as:
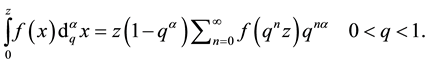 (5)
(5)
Similarly
 (6)
(6)
For the integer number n, the quantum integer is defined as a [n]q (bracket n) such that
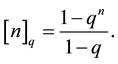 (7)
(7)
In [16] , for  q-derivative operator
q-derivative operator  is defined as:
is defined as:
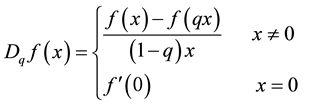 (8)
(8)
and the generalized q-derivative for 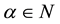 is defined as:
is defined as:
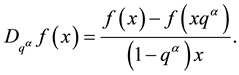 (9)
(9)
Similarly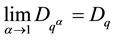 .
.
Analytical calculation of q-integrals similar to the ordinary integrals leads to extending these integrals as a series expansion, [10] applies q-taylor expansion, [17] introduces q-integrals inequalities and [16] takes advantage of hypergeometricpolynomials to express the q-integralas a series expansion, the inequalities in [17] help to find limit for q integrals, [12] generalizes the procedures of integral to some kind of q-integrals, and finally we generalize the procedure similar in [13] [18] .
3. Numerical Approximation of q-Integral
For a given value of q the following approximation can be established
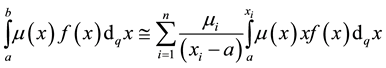 (10)
(10)
where![]() ,
, ![]() s and
s and ![]() s are the nodes and weights respectively and must be determined. Similar to the definition of precision degree for integral, we have for the q-integral
s are the nodes and weights respectively and must be determined. Similar to the definition of precision degree for integral, we have for the q-integral
![]() (11)
(11)
By calculating the limits in either side we get
![]() (12)
(12)
Similar to the algorithm used in [5] we have the following theorem:
Theorem: The q-normal equations for ![]() and
and![]() , gives the following system of equations
, gives the following system of equations
![]() (13)
(13)
Proof: Without losing the generality, for![]() ,
, ![]() ,
, ![]() , [a,b] = [0,1] from (12) we have
, [a,b] = [0,1] from (12) we have
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
Hence, we have the following system of equations
![]() (17)
(17)
This can be summarized as the following matrix form such that for![]() :
:
![]() (18)
(18)
where
![]() (19)
(19)
is a Toeplitz matrix [10,11], whose entries are quantum numbers so, we call it quantum Toeplitz matrix, an especial form of n-diameter quantum matrix and keeps the non-singularity or singularity properties of the original matrix, because all elements of matrix have been changed simultaneously, positive Toplitz matrices, quantum matrices and Inversion of Toeplitz matrices are considered in [19] - [23] , so for having a unique solution, the same conditions for the original system of equations (q = 1) must be satisfied (12) for the different values of q, the elements of vector C and the nodes satisfy in the following characteristics equation [13]
![]() (24)
(24)
Now, the roots of above characteristics equations are the appropriate nodes, satisfying in the system of simultaneous equations, then having these nodes the weighs μi can be evaluated, and by applying these values in (12) the system of Equation (13) will be obtained to evaluate the approximate values of the quantum integral, obviously the unknown in the system of equations depend upon the quantum parameter![]()
In Section 3 we illustrate the algorithm for the numerical approximation of q-integral and some examples to illuminate the exactness of the method.
4. Algorithm for the Numerical Solution
We start the algorithm by the small values of n and similar method can be extended to any value of n, let n = 2, then for the evaluated values of xi s and μi
![]() (25)
(25)
characteristic equation is
![]() (26)
(26)
The system of equations is:
![]() (27)
(27)
![]() (28)
(28)
Then
![]() (29)
(29)
different approximation can be expected for the different values of q, which for some values of q, 0 < q < 1, q-integral may have minimum error, if ![]() then matrix entry
then matrix entry![]() ; i = 1, 2, …and if
; i = 1, 2, …and if ![]() then
then![]() , for the other values of say q = 0.1 we have:
, for the other values of say q = 0.1 we have:
![]() (30)
(30)
This gives
![]() (31)
(31)
Then the characteristic equation is
![]() (32)
(32)
Gives the following roots
![]()
By solving the linear system we obtain μ1, μ2
![]() (33)
(33)
![]()
And the numerical q-integration formula for q = 0.1 can be evaluated from
![]() (34)
(34)
![]() (35)
(35)
Let n = 3, then for the evaluated values of xis and, xis
![]() (36)
(36)
Characteristics equations is
![]() (37)
(37)
For n = 3, the system of equations is
![]() (38)
(38)
![]() (39)
(39)
Similarly, for q = 0.1 numerical q-integration is
![]() (40)
(40)
This gives
![]() (41)
(41)
And a characteristics equation is:
![]() (42)
(42)
With the roots as follows
![]()
Now, for calculating ![]() the linear system should be solved
the linear system should be solved
![]() (43)
(43)
And we will have
![]()
Finally the numerical q-integration for q = 0.1 takes the following form
![]() (44)
(44)
Tables 1-3 give the q-integral approximation for n = 2, 3, 4 respectively and some values of q.
![]()
Table 1. Give q-integral approximation for n = 2 and different values of q.
![]()
Table 2. Give the q-integral approximation for n = 3 and different values of q.
![]()
Table 3. Give the q-integral approximation for n = 4 and different values of q.
![]()
![]()
Table 4. Give the q-integral approximation for n = 2 and almost extreme value of q = 0.99999 for three different integrants in a specified interval.
5. Error Analysis and Application of q-Integral for Integral Approximation
The numerical values show for all values of n the error of q-integrations fluctuate for different values of q, it seems q = 0.70 gives the worse error almost for all values of n, the errors decreases as q approaches to the extreme values 0 and 1. Using this result and (3) the q-integral can be calculated for very large value of q approaching to 1 which will approximate the ordinary integrals whose q-integrals is easier than ordinary integrals by using q-integral approximation for n = 2 and different values of q, as illustrated in Table 4 and following the examples, where
![]()
6. Conclusion
In this paper, a new algorithm for the numerical approximation of q-integration based on q-calculation of appropriate nodes and weights is introduced. The evaluation of nodes and weight is based on q-integral error minimization, as expected in the numerical examples which give a good approximation in comparison with exact solutions for the given values of q and fixed n. As the q-fractional integration can be transferred to q-integrals, the procedure is also applicable for q-fractional integration, and also improper integrals for the large values of q.