1. Introduction
The purpose of this paper is to draw attention to a certain property of curvature which differs in a remarkable way between Lorentz geometry and Euclidean geometry. However, the author’s ambition is rather to pose interesting questions than to give ready answers. Coarsely speaking, the main idea is that in Lorentz geometry, rotating objects may be less curved (as measured by the integral of the square of the scalar curvature) than non-ro- tating ones. The original motivation for this mathematical problem comes from physics, but the author does not make any claims about implications in the other direction, except that any kind of deeper understanding of Lorentz geometry may eventually turn out to be useful for uniting general relativity and quantum mechanics. In any case, the problems that arise also have an independent mathematical interest.
It has been known for more than 85 years that, through the work of P. A. M. Dirac [1] , the spin of elementary particles is something which necessarily appears when we extend non-relativistic quantum mechanics to relativistic situations. The theory of spin is now a well understood part of quantum physics within the framework of special relativity. But, as for all of quantum mechanics, we do not really know what this will correspond to within the framework of general relativity. It may therefore have some interests to note that even within a completely classical theory, some kinds of spin property may exist in the following sense.
In [2] [3] , the author has investigated a theory in which the square of the scalar curvature, coarsely speaking, plays the role of mass-energy in the system under study. If it is really a property of Lorentz geometry that rotating objects may have lower energy than non-rotating ones, this would imply a picture where rotating objects are the natural ground states, in very much the same way as physicists usually explain stability of various configurations by saying that they minimize the energy. Clearly, one should not over-exaggerate the similarity with quantum mechanics. And we do not even know if the concepts of differential geometry, e.g. curvature, will have any exact meaning in a future synthesis between general relativity and quantum physics. Still, in view of the fact that such a synthesis has turned out to be so elusive, it is the opinion of the author that all similarities between the two theories that we can find have a potential interest.
In the following we will only present a simple example of this phenomenon, but even in this situation the computations are by far too complicated to be carried out by hand. In fact, the results in this paper depend heavily on the use of computers and so far there is no complete, satisfactory mathematical theory behind them. On the other hand, for the understanding of the general case, computers will certainly not be enough.
Considering some topologically non-trivial manifolds attached to an otherwise flat three-dimensional space to form a new manifold M, the reader may think of some kinds of wormhole (see Section 2). In this paper, we will refer to such manifolds as topological objects. We now want to study what happens if we let a topological object rotate around some axis. However, since we are mainly interested in Lorentz geometry, it is not at all clear from the beginning what the word rotation should refer to, so in Section 3 we will introduce the idea of a quasi-rota- tion, and in Section 4 we discuss how to measure curvature. In Section 5 we then apply the ideas of the previous two sections to the wormhole of Section 2.
In the case of usual Euclidean geometry, it seems very reasonable (although mathematically non-obvious) to expect that the total amount of scalar curvature should be minimized when the object is not rotating, and that it should grow with increasing speed of rotation. In fact, the very process of rotating should tend to bend the geometry inside the object, which ought to generate curvature. This is also what will come out in the example which we will consider here. What is curious, however, is that this does no longer seem to hold if we replace Euclidian geometry with Lorentz geometry (see Sections 6 and 7).
This leads us to formulate some open questions in Section 8. For example, is it a common fact of Lorentz geometry that rotating topological objects may have smaller total curvature in this sense than the corresponding non-rotating ones? In particular, one may wonder if topological objects which minimize the integral of the square of the scalar curvature are always rotating in some sense. To make this question somewhat more precise, we will in this paper consider minimizing under the extra condition that the total space-time volume is fixed.
Let us also mention that, in the example to be discussed, the fact that the total curvature may decrease when we start to rotate does not appear to be a local geometric property: at some points of the manifold the scalar curvature may increase and at other points it may decrease, as will be seen in (6.3) below. Thus, this is a global property of the scalar curvature, rather than a local one.
2. An Example of a Wormhole
We start by making the idea of a “wormhole” in Euclidian three-space more precise. We first remove the two open balls 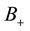 and
and 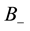 of radius one with centers at the points
of radius one with centers at the points  and
and 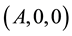 where A is some number larger than 1 (for the most of this paper we will in fact assume that A is large). To the remaining set
where A is some number larger than 1 (for the most of this paper we will in fact assume that A is large). To the remaining set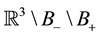 , we attach a cylinder
, we attach a cylinder  to form a new manifold M in such a way that the boundaries
to form a new manifold M in such a way that the boundaries 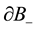 and
and 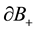 are identified with the ends
are identified with the ends 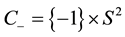 and
and 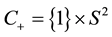 of the cylinder in an obvious way. Furthermore, we introduce usual spherical coordinates
of the cylinder in an obvious way. Furthermore, we introduce usual spherical coordinates 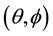 on
on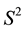 , and then add a third coordinate
, and then add a third coordinate  to get coordinates
to get coordinates  on all of C. On the other hand, we can also introduce spherical coordinates centered at
on all of C. On the other hand, we can also introduce spherical coordinates centered at 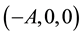 and
and 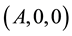 respectively, by setting
respectively, by setting
![]() (2.1)
(2.1)
where we have adopted the convention that ![]() but
but![]() . The topological and differentiable structures on M are then determined by identifying
. The topological and differentiable structures on M are then determined by identifying ![]() with
with ![]() in the case when
in the case when![]() , and
, and ![]() with
with ![]() when
when![]() . In the following computations, we will, in view of these identification, often drop the − and + signs and without ambiguity simply write
. In the following computations, we will, in view of these identification, often drop the − and + signs and without ambiguity simply write ![]() for all three sets of coordinates, since they do in fact define coordinates in a neighborhood of C, although they, of course, in no way define a global coordinate system on M. In fact, all computations below will be carried out when
for all three sets of coordinates, since they do in fact define coordinates in a neighborhood of C, although they, of course, in no way define a global coordinate system on M. In fact, all computations below will be carried out when![]() , and other values of r only play a role when it comes to determining the boundary conditions for the cylinder. As a matter of terminology, one can refer to the region where
, and other values of r only play a role when it comes to determining the boundary conditions for the cylinder. As a matter of terminology, one can refer to the region where ![]() as the cylindrical region of the manifold
as the cylindrical region of the manifold ![]() and to the rest as the flat region. In addition, the two boundaries between these regions, where
and to the rest as the flat region. In addition, the two boundaries between these regions, where ![]() and
and ![]() respectively, will be referred to as the upper and lower boundaries of the cylinder.
respectively, will be referred to as the upper and lower boundaries of the cylinder.
Having thus defined the manifold structure and corresponding coordinates, we now proceed to define a metric on M. In fact, outside the cylindrical region, we will simply use the usual Euclidian metric ![]() which in spherical coordinates takes the well-known form
which in spherical coordinates takes the well-known form
![]() (2.2)
(2.2)
On the other hand, inside the cylindrical part C, we want to define the metric in a way which makes it reasonably regular at the boundaries of the cylinder. The reader may check that the following simple choice makes the metric ![]() across the cuts at
across the cuts at ![]() and
and![]() , thus avoiding singular contributions to the curvature:
, thus avoiding singular contributions to the curvature:
![]() (2.3)
(2.3)
Finally, we note that the 3-dimensional volume element for ![]() takes the form
takes the form
![]() (2.4)
(2.4)
3. Quasi-Rotations
In this section, we study what happens when we rotate a topological object, defined by a manifold M as in Section 2. A very natural idea would be to say that the best method should be to find exact solutions to the field equations as has been done e.g. for rotating black holes in the form of the Kerr metric (see [4] [5] ). However, in the present situation this does not seem to be a possible approach for several reasons, at least not for the time being. First of all, it is not likely that there is such a solution for an arbitrary topological object. Secondly, in view of the fact that there is in general no spherical symmetry near the object, such a solution may, even if it exists, be very difficult to describe analytically. Thirdly, even if we find such a solution, it is not likely to be unique in view of the fact that rotation is not a very well-defined concept in general relativity.
For these reasons, we will make use of a much more simpleminded approach. We will in this paper only investigate very slow rotations, and in this situation we can therefore start from the usual idea of a rotation in Euclidian space and then modify it slightly for our needs. This is clearly not the ideal way to proceed. Nevertheless, it will turn out that it is still good enough for illustrating the main point of this paper.
We first introduce some notation. Let B be an open sphere, centered at the origin in![]() , and let
, and let ![]() be the (non-trivial) manifold which we use to replace B to create a topological object, i.e.
be the (non-trivial) manifold which we use to replace B to create a topological object, i.e.
![]() (3.1)
(3.1)
For example, in the case of the simple wormhole of Section 2, B is a sphere which contains ![]() and
and![]() , and we get
, and we get
![]() (3.2)
(3.2)
We can now trivially extend M to four dimensions by adding a time-coordinate t to get![]() . Clearly, N can be thought of as representing a topological object at rest.
. Clearly, N can be thought of as representing a topological object at rest.
To see how to define a rotation, we start with the trivial case where M is simply equal to![]() . From a four- dimensional point of view, a rotation of
. From a four- dimensional point of view, a rotation of ![]() with angular velocity
with angular velocity ![]() around an axis
around an axis ![]() can be thought of as a map
can be thought of as a map
![]() (3.3)
(3.3)
where ![]() and
and ![]() is the usual 3-dimensional rotation operator which rotates each vector around the
is the usual 3-dimensional rotation operator which rotates each vector around the ![]() - axis through the angle
- axis through the angle![]() . This map, together with its image, can be said to represent the four-dimensional picture of a rotation of three-dimensional space, although in this case of course the image is just
. This map, together with its image, can be said to represent the four-dimensional picture of a rotation of three-dimensional space, although in this case of course the image is just![]() .
.
To rotate a more general topological object, we need to construct a new map and a new image manifold which outside of ![]() looks exactly the same as in the above trivial example. A somewhat formal mathematical way to proceed is the following:
looks exactly the same as in the above trivial example. A somewhat formal mathematical way to proceed is the following:
To define the four-manifold describing a rotation with angular velocity ![]() around the axis
around the axis![]() , we can set
, we can set
![]() (3.4)
(3.4)
where the union over ![]() is a disjoint union of different copies of
is a disjoint union of different copies of![]() , and where we identify a point
, and where we identify a point ![]() with the corresponding point
with the corresponding point![]() .
.
In a little bit less formal language, this can be viewed as just a stack of copies of the manifold M (one for each![]() ), each rotated by the angle
), each rotated by the angle ![]() around
around![]() , and where the flat region outside the object is naturally identified with ordinary four-space. It is also clear that in the case
, and where the flat region outside the object is naturally identified with ordinary four-space. It is also clear that in the case![]() ,
, ![]() simply reduces to
simply reduces to![]() .
.
Rather than pursuing the mathematical formalism further, let us just state some more or less obvious properties of this construction which can in fact be used to characterize![]() .
.
1) For each![]() , the map
, the map ![]() extends from
extends from ![]() to a diffeomorphism
to a diffeomorphism![]() , which on
, which on ![]() is just the map which identifies
is just the map which identifies ![]() with the corresponding point
with the corresponding point![]() .
.
2) For each t, ![]() gives an isometry
gives an isometry![]() .
.
These two conditions essentially characterize the rotation, and they can in fact also be used to define the differentiable structure on![]() . However, in the following it will also be interesting to study the rotation as a function of
. However, in the following it will also be interesting to study the rotation as a function of![]() . In particular, we do not want a change in
. In particular, we do not want a change in ![]() to change the total volume. Hence, we add a third condition:
to change the total volume. Hence, we add a third condition:
3) The map ![]() preserves the 4-volume element
preserves the 4-volume element![]() .
.
Clearly, we can not in general demand that the map ![]() should be an isometry
should be an isometry![]() . The last condition can in a sense be regarded as a kind of weak substitute: if we cannot preserve the whole metric, then we can at least preserve the volume element.
. The last condition can in a sense be regarded as a kind of weak substitute: if we cannot preserve the whole metric, then we can at least preserve the volume element.
If the four-manifolds ![]() and maps
and maps![]() ,
, ![]() for some
for some![]() , satisfy the above conditions (1)-(3), and if the dependence on
, satisfy the above conditions (1)-(3), and if the dependence on ![]() is smooth (real analytic), we will in the following refer to the family of all these manifolds and maps as a quasi-rotation.
is smooth (real analytic), we will in the following refer to the family of all these manifolds and maps as a quasi-rotation.
Clearly, such a quasi-rotation does not in itself involve Lorentz geometry in any essential way, and in fact, the idea makes equally good sense for a positive definite metric as for a pseudo-metric. Also, it is not assumed to represent any kind of physical geometry that in itself would have physical significance. A more realistic geometry for a rotating object will probably involve the time-coordinate t in a much more complicated way. In addition, there is nothing unique about the way in which we define a quasi-rotation, even if the axis of rotation and the angular speed ![]() are given. The importance of this construction only lies in the fact, that it can be used as a tool to investigate if non-rotating objects are minimizing or not.
are given. The importance of this construction only lies in the fact, that it can be used as a tool to investigate if non-rotating objects are minimizing or not.
Since the spacial coordinates and the axis of rotation is at our choice, we will for definiteness always use a fixed axis. Hence, we will drop ![]() from the notation from now on.
from the notation from now on.
4. Curvature and Periodicity
In this section, we discuss how to measure curvature. In the simplest case of an object N at rest, with a metric of the simple form![]() , where
, where ![]() is a time-independent positive definite metric on
is a time-independent positive definite metric on![]() , which is equal to the standard flat metric outside B, we can measure the curvature of the object by the integral
, which is equal to the standard flat metric outside B, we can measure the curvature of the object by the integral
![]() (4.1)
(4.1)
where R denotes (4-dimensional) scalar curvature, and where ![]() denotes the three-dimensional volume measure induced by
denotes the three-dimensional volume measure induced by![]() .
.
In the next simplest case of a quasi-rotation as in Section 3, we can, using condition II in the definition of a quasi-rotation, still measure the total curvature by integrating ![]() for a fixed t, since the value of this integral will in fact be independent of t.
for a fixed t, since the value of this integral will in fact be independent of t.
In more complicated situations, (4.1) may no longer make any sense, since there may be no natural unique way of defining surfaces of constant time if there is no natural choice for the time-coordinate.
Nevertheless, it is possible to measure curvature for more general objects. If we consider the situation where space-time outside the object is flat and the object itself is, except for internal movements, at rest, then clearly we can unambiguously speak of time in the exterior in the sense of the time in the rest-frame of the object.
Suppose that we can extend the surfaces ![]() of constant time from the exterior into the object itself in some way. Then we can put
of constant time from the exterior into the object itself in some way. Then we can put
![]() (4.2)
(4.2)
where ![]() is a time-interval of length
is a time-interval of length![]() ,
, ![]() is the 4-dimensional volume measure on N, and
is the 4-dimensional volume measure on N, and ![]() is the region between the extended surfaces
is the region between the extended surfaces ![]() and
and![]() . It is not difficult to show that in the case of quasi-rotations where the surfaces
. It is not difficult to show that in the case of quasi-rotations where the surfaces ![]() are given by
are given by![]() , (4.2) reduces to the 3-dimen- sional integral in (4.1).
, (4.2) reduces to the 3-dimen- sional integral in (4.1).
It is worth noting that the extended surfaces ![]() do not in general have to have anything to do with the metric structure. In particular, they should not necessarily be interpreted as surfaces of equal time in inside the object. However, for the limit in (4.2) to exist and in addition be independent of the particular choice of
do not in general have to have anything to do with the metric structure. In particular, they should not necessarily be interpreted as surfaces of equal time in inside the object. However, for the limit in (4.2) to exist and in addition be independent of the particular choice of![]() , we still need to impose some extra condition, like e.g. periodicity in the sense that for some
, we still need to impose some extra condition, like e.g. periodicity in the sense that for some![]() , the natural time- translation map
, the natural time- translation map ![]() on
on![]() , can be extended to an isometry
, can be extended to an isometry ![]() which maps
which maps ![]() onto
onto ![]() for all t. Since we will not make use of this generalization in this paper, we will not pursue this question further here.
for all t. Since we will not make use of this generalization in this paper, we will not pursue this question further here.
5. A Four-Dimensional Metric for the Rotating Wormhole
The purpose of this section is to sketch how to construct a quasi-rotation of the wormhole in Section 2. This essentially boils down to defining a metric on ![]() for all small
for all small ![]() and, in view of the discussion in the previous sections, it is really enough to do the construction for
and, in view of the discussion in the previous sections, it is really enough to do the construction for![]() . Still, the construction is very technical and for the purpose of this paper we have chosen to simplify it in two ways:
. Still, the construction is very technical and for the purpose of this paper we have chosen to simplify it in two ways:
Firstly, we will only work with very slow rotations and, as a consequence we will, just as in Section 3, partly treat the motion in a non-relativistic way, even in the case of an indefinite metric. This may appear odd at first sight, but since the theory of general relativity gives no unique way of constructing the geometry of a rotating object, the Lorentz transform may be no more natural than the Galileo transform in this case. As a matter of fact, to illustrate the point that we want to make, either one of them would do, which is why we have chosen the least technical one.
Secondly, we will only consider the case![]() . Technically, this means that we will neglect small terms near the boundaries of the cylinder. This second simplification would not be so difficult to deal with, but the main difficulty would still remain, namely to deal with the fact that our real goal is to do the construction for metrics which are minimizing, see further Section 8. Since the main interest in this paper is Lorentz geometry, we will concentrate on this case and leave the Euclidian case to the reader.
. Technically, this means that we will neglect small terms near the boundaries of the cylinder. This second simplification would not be so difficult to deal with, but the main difficulty would still remain, namely to deal with the fact that our real goal is to do the construction for metrics which are minimizing, see further Section 8. Since the main interest in this paper is Lorentz geometry, we will concentrate on this case and leave the Euclidian case to the reader.
As in Section 3, we extend the manifold M of Section 2 to four dimensions by adding a time-variable t, to obtain a 4-manifold ![]() with coordinates
with coordinates ![]() near the cylinder. Also, the Minkowski metric
near the cylinder. Also, the Minkowski metric
![]() (5.1)
(5.1)
on ![]() can clearly be extended to a
can clearly be extended to a ![]() -metric on all of N by putting it equal to (compare (2.3))
-metric on all of N by putting it equal to (compare (2.3))
![]() (5.2)
(5.2)
on![]() , where C is the cylindrical part, thus giving rise to a model for a wormhole at rest.
, where C is the cylindrical part, thus giving rise to a model for a wormhole at rest.
To construct the quasi-rotation of M, we assume the rotation to take place around the y-axis with uniform speed in the counter-clockwise direction. We therefore assume that the two boundaries located at ![]() and
and![]() , are moving downwards and upwards (with respect to the positive z-axis in the xz-plane) respectively, with speed v. In the following we will use v as a measure for the speed of rotation, although it is actually related to the angular velocity
, are moving downwards and upwards (with respect to the positive z-axis in the xz-plane) respectively, with speed v. In the following we will use v as a measure for the speed of rotation, although it is actually related to the angular velocity ![]() by the formula
by the formula![]() . This is a useful convention since it prevents A from showing up in the final results below. To avoid technical details as far as possible, we assume that
. This is a useful convention since it prevents A from showing up in the final results below. To avoid technical details as far as possible, we assume that ![]() so that we can assume that the upper boundary at
so that we can assume that the upper boundary at ![]() is simply moving upwards parallel to the z-axis, and that the coordinates
is simply moving upwards parallel to the z-axis, and that the coordinates ![]() of its rest frame (and correspondingly, the coordinates
of its rest frame (and correspondingly, the coordinates ![]() of the rest frame of the lower boundary moving downwards) are related to the original coordinates
of the rest frame of the lower boundary moving downwards) are related to the original coordinates ![]() by the formulas
by the formulas
![]() (5.3)
(5.3)
We note that the movement of the wormhole destroys the connection between the metric (2.3) of the cylindrical region and the Minkowski metric of the flat region. Hence, we must next investigate how the metric should be modified for ![]() in order to fit onto the outside at the boundaries
in order to fit onto the outside at the boundaries ![]() and
and![]() . We first concentrate on the latter case.
. We first concentrate on the latter case.
To this end, we note that from (the right hand part of) (5.3) we obtain ![]() which gives
which gives ![]() and together with
and together with ![]() further implies
further implies
![]() (5.4)
(5.4)
Next we note from (2.1) that ![]() which gives
which gives![]() . This, together with the formula
. This, together with the formula
![]() (5.5)
(5.5)
(which is analogous to (2.2)) when substituted into (5.4) gives
![]() (5.6)
(5.6)
where we have again dropped the + sign and written t instead of![]() .
. ![]() is thus the boundary condition that the modified metric of the cylindrical region has to fulfill at the boundary
is thus the boundary condition that the modified metric of the cylindrical region has to fulfill at the boundary![]() .
.
Carrying out the similar computations at the other end of the wormhole where![]() , we obtain (now instead using
, we obtain (now instead using ![]() and
and![]() ),
),
![]() (5.7)
(5.7)
From (2.3), (5.6) and (5.7) it is now evident that the easiest way to interpolate between ![]() and
and ![]() is to let
is to let
![]() (5.8)
(5.8)
for all![]() . In fact, this metric
. In fact, this metric ![]() does satisfy the first two conditions in the definition of a quasi-rota- tion in Section 3, at least if
does satisfy the first two conditions in the definition of a quasi-rota- tion in Section 3, at least if![]() .
.
To fulfill the third condition, we will have to modify the metric slightly. The volume element of the metric in the interior is given by
![]() (5.9)
(5.9)
where from (5.8) we have that
![]() (5.10)
(5.10)
![]() (5.11)
(5.11)
![]() (5.12)
(5.12)
Hence we see that the function G in (5.9) is given by
![]() (5.13)
(5.13)
where furthermore the function
![]() (5.14)
(5.14)
equals 1 to first order at the endpoints![]() . If we therefore redefine the metric
. If we therefore redefine the metric ![]() in (5.8) above by putting
in (5.8) above by putting
![]() (5.15)
(5.15)
then clearly we get a metric with the same volume element as in the non-rotating case,
![]() (5.16)
(5.16)
independently of v, and furthermore the regularity properties at ![]() are essentially similar to the case
are essentially similar to the case![]() .
.
6. Computation of the Curvature Integral
In this Section we will now attempt to compute the curvature integral I in (4.1) for the metrics ![]() in (5.15) as a function of v (rather than of
in (5.15) as a function of v (rather than of![]() ). Since the coefficients of the metric in (5.15), as well as the volume element in (5.16), are independent not only of t but also of
). Since the coefficients of the metric in (5.15), as well as the volume element in (5.16), are independent not only of t but also of![]() , the corresponding integration readily disappears from the integral and we are left with
, the corresponding integration readily disappears from the integral and we are left with
![]() (6.1)
(6.1)
To compute this integral we make use of the built-in tensor calculus of Maple, since a direct computation by hand is virtually impossible (the Maple output for the scalar curvature covers 15 pages). Thus, using first Taylor expansion in v to order 5 and then numerical integration, Maple gives
![]() (6.2)
(6.2)
Hence, we can see that ![]() is not a minimum of I(v) but rather represents a local maximum.
is not a minimum of I(v) but rather represents a local maximum.
We now turn to the question whether the behavior in (6.2) is global or local. To this end, we simply split the
domain of integration in (6.1) up into 2000 small rectangles of the form ![]()
with ![]() and
and![]() . An obvious but tedious testing procedure (done by the computer) reveals that most
. An obvious but tedious testing procedure (done by the computer) reveals that most ![]() in fact behaves like in (6.2), but for instance
in fact behaves like in (6.2), but for instance
![]() (6.3)
(6.3)
Thus, the fact that ![]() is a local maximum rather than a minimum can not be explained locally.
is a local maximum rather than a minimum can not be explained locally.
7. The Euclidian Case
For comparison we can also carry out the analogous computations in the case of a positive definite metric![]() . The reader may check that the extension to the cylindrical region corresponding to (5.15) will be
. The reader may check that the extension to the cylindrical region corresponding to (5.15) will be
![]() (7.1)
(7.1)
where now
![]() (7.2)
(7.2)
Again using Maple, we similarly obtain
![]() (7.3)
(7.3)
Thus we see that in this case, ![]() does give a minimum for I(v) as one would expect.
does give a minimum for I(v) as one would expect.
8. Open Questions
It is the belief of the author that the difference between formulas (6.2) and (7.3) reflects an important difference between Lorentz geometry and Euclidian geometry. However, the computations in this paper are very far from giving any definite solutions to all the problems that arise. In particular, the simple wormhole in Section 2 is too much simple to say something definite about the general case. Let us therefore here summarize some of the open questions:
Question 1. In the case of Lorentz geometry, is it the case that for any manifold M with metric g and curvature integral![]() , we can define a quasi-rotation with the property that the corresponding function
, we can define a quasi-rotation with the property that the corresponding function ![]() will have a local maximum at
will have a local maximum at![]() ?
?
Remark 1. Formulated in this way, it is quite likely that the question does not have an affirmative answer. For instance, it is quite possible that the behavior of ![]() depends on the topological type of M in a complicated way.
depends on the topological type of M in a complicated way.
Nevertheless it could be that the question could have an affirmative answer for some reasonably large classes of manifold.
But there is also another way of formulating the problem. From the point of view of this paper, the most interesting topological objects are those which minimize the curvature in the sense of (4.1). Thus one could try to ask the following
Question 2. In the case of Lorentz geometry, is it true that a non-rotating manifold with curvature integral ![]() is never minimizing?
is never minimizing?
If this is true, a reasonable way of proving it would be to construct some kinds of quasi-rotations of all such manifolds. Similarly one may ask, in the case of Euclidean geometry, if it is true that minimizing manifolds are always non-rotating.
The point is that the question itself is now independent of the somewhat technical definition of a quasi-rotation in Section 3. In fact, the word non-rotating manifold can be replaced by invariance under time-translation, and also we can allow for more general metrics and replace the condition of flatness outside B by a weaker asymptotic condition.
It is however a problem with the objects in this paper that it is not at all clear under what circumstances I have a minimum, even if we restrict ourselves to the case where the space-time volume is fixed in some appropriate sense. Hence, there are many existence and regularity questions which have to be considered if we want to investigate rotating objects more deeply.