A Unified Approach for the Multivariate Analysis of Contingency Tables ()
1. Introduction
In multivariate analysis, it is usual to link several methods in a closed expression, which depends on a set of parameters. Thus, in cluster analysis, some criteria (single linkage, complete linkage, median), can be unified by using parametric coefficients. The biplot analysis on a centered matrix , is based on the singular value de- composition (SVD)
, is based on the singular value de- composition (SVD)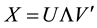 . The general solution is
. The general solution is 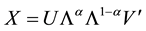 with
with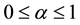 , providing the GH, JK, SQ and other biplot types depending on
, providing the GH, JK, SQ and other biplot types depending on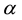 . Also, some orthogonal rotations in factor analysis (varimax, quartimax) are particular cases of an expression depending on one or two parameters.
. Also, some orthogonal rotations in factor analysis (varimax, quartimax) are particular cases of an expression depending on one or two parameters.
There are several methods for visualizing the rows and columns of a contingency table. These methods can be linked by using parameters and some well-known matrices. This parametric approach shows that correspon- dence analysis (CA), Hellinger distance analysis (HD), non-symmetric correspondence analysis (NSCA) and log-ratio analysis (LR), are particular cases of a general expression. In these methods, the decomposition of the inertia is used as well as a generalized version of Pearson contingency coefficient. With the help of triangular matrices, it is also possible to perform two analyses, Taguchi’s analysis (TA) and double accumulative analysis (DA), both based on cumulative frequencies. This paper unifies and extends some results by Cuadras and Green- acre [1] -[4] .
2. Weighted Metric Scaling
A common problem in data analysis consists in displaying several objects as points in Euclidean space of low dimension.
Let  be a set with
be a set with 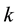 objects,
objects,  a distance function on
a distance function on 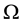 providing the
providing the 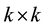 Eu- clidean distance matrix
Eu- clidean distance matrix , where
, where 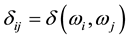 Let
Let 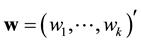 a weight vector such that
a weight vector such that 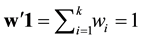 with
with  and
and  the column vector of ones.
the column vector of ones.
The weighted metric scaling (WMS) solution using ![]() finds the spectral decomposition
finds the spectral decomposition
![]() , (1)
, (1)
where ![]() is the identity matrix,
is the identity matrix, ![]() ,
, ![]() is
is ![]() diagonal with
diagonal with ![]() positive eigenvalues arranged in descending order,
positive eigenvalues arranged in descending order, ![]() is
is ![]() such that
such that![]() , and
, and ![]() [5] .
[5] .
The ![]() matrix
matrix ![]() contains the principal coordinates of
contains the principal coordinates of![]() , which can be represented as a configuration of
, which can be represented as a configuration of ![]() points
points ![]() in Euclidean space. This means that the Euclidean distance between the points
in Euclidean space. This means that the Euclidean distance between the points![]() ,
, ![]() with coordinates the rows
with coordinates the rows![]() ,
, ![]() of
of![]() , equals
, equals![]() .
.
The geometric variability of ![]() with respect to
with respect to ![]() is defined by
is defined by
![]() .
.
The geometric variability (also called inertia) can be interpreted as a generalized variance [6] .
If ![]() and
and ![]() is the column vector with the diagonal entries in
is the column vector with the diagonal entries in![]() , then
, then![]() . Since
. Since ![]() and
and![]() , we have
, we have![]() . Thus, if
. Thus, if![]() , the geometric variability is
, the geometric variability is
![]() .
.
We should use the first m columns of ![]() to represent the
to represent the ![]() objects in low dimension
objects in low dimension![]() , usually
, usually![]() . This provides an optimal representation, in the sense that the geometric variability taking
. This provides an optimal representation, in the sense that the geometric variability taking ![]() first di- mensions is
first di- mensions is ![]() and this quantity is maximum.
and this quantity is maximum.
3. Parametric Analysis of Contingency Tables
Let ![]() be an
be an ![]() contingency table and
contingency table and ![]() the correspondence matrix, where
the correspondence matrix, where![]() . Let
. Let ![]() and
and![]() ,
, ![]() ,
, ![]() ,
, ![]() , the vectors and diagonal matrices with the marginal frequencies of
, the vectors and diagonal matrices with the marginal frequencies of![]() . In order to represent the rows and columns of
. In order to represent the rows and columns of![]() , Goodman [7] intro- duces the generalized non-independence analysis (GNA) by means of the SVD:
, Goodman [7] intro- duces the generalized non-independence analysis (GNA) by means of the SVD:
![]() ,
,
where ![]() is diagonal with the singular values in descending order, and
is diagonal with the singular values in descending order, and ![]() are matrices of appropriate order with
are matrices of appropriate order with![]() , and
, and ![]() orthogonal.
orthogonal.![]() , with
, with![]() , is any monotonically increasing function. Here
, is any monotonically increasing function. Here
![]() with
with![]() , means
, means![]() . The principal coordinates for rows and columns are given by
. The principal coordinates for rows and columns are given by
![]() ,
,![]() . Clearly GNA reduces to CA when
. Clearly GNA reduces to CA when![]() .
.
A suitable choice of ![]() is the Box-Cox transformation
is the Box-Cox transformation
![]()
With this transformation, let us consider the following SVD depending on three parameters:
![]() , (2)
, (2)
where ![]() and
and![]() . Then the principal coordinates for the
. Then the principal coordinates for the ![]() rows and the standard coordinates for the
rows and the standard coordinates for the ![]() columns of
columns of ![]() are given by
are given by ![]() and
and![]() , respectively, in the sense that these coordinates reconstitute the model:
, respectively, in the sense that these coordinates reconstitute the model:
![]() .
.
However, different weights are used for the column representation, e.g.,![]() . Implicit with this (row) representation is the squared distance between rows
. Implicit with this (row) representation is the squared distance between rows
![]() . (3)
. (3)
The first principal coordinates account for a relative high percentage of inertia, see Section 2. This parametric approach satisfies the principle of distributional equivalence and has been explored by Cuadras and Cuadras [2] and Greenacre [4] . Here we use Greenacre’s parametrization.
The geometric variability for displaying rows, is the average of the distances weighted by the row marginal frequencies:
![]() ,
,
where ![]() is the
is the ![]() matrix of squared parametric distances (3).
matrix of squared parametric distances (3).
For measuring the dispersion in model (2), let us introduce the generalized Pearson contingency coefficient
![]() .
.
Note that ![]() if
if![]() , i.e., under “statistical independence” between row and column vari- ables. In general
, i.e., under “statistical independence” between row and column vari- ables. In general![]() .
.
The unified approach for all methods (centered and uncentered) discussed below, are given in Table 1. It is worth noting that, from
![]() , (4)
, (4)
the centered ![]() and uncentered
and uncentered ![]() solutions coincide in CA, NSCA and TA (Taguchi’s analysis, see below).
solutions coincide in CA, NSCA and TA (Taguchi’s analysis, see below).
To give a WMS approach compatible with (1), we mainly consider generalized versions without right-
centering, i.e., post-multiplying ![]() by
by![]() . In fact, we can display columns in the same
. In fact, we can display columns in the same
![]()
Table 1. Four methods for representing rows and columns in a contingency table.
graph of rows without applying this post-multiplication. To do this compute the SVD ![]() with D diagonal and HI the unweighted
with D diagonal and HI the unweighted ![]() centering matrix. Then
centering matrix. Then ![]() and if we take prin- cipal coordinates
and if we take prin- cipal coordinates ![]() for the rows, and identify each column as the dummy row profile
for the rows, and identify each column as the dummy row profile![]() , then the centered projection
, then the centered projection ![]() provides standard coordinates for the columns, see [2] [3] .
provides standard coordinates for the columns, see [2] [3] .
4. Testing Independence
Suppose that the rows and columns of ![]() are two sets of categorical variables with
are two sets of categorical variables with ![]() and
and ![]() states, and that
states, and that ![]() is the observed frequencies of the corresponding combination, according to a multinomial model. Assuming
is the observed frequencies of the corresponding combination, according to a multinomial model. Assuming![]() , the test for independence between row and column variables can be performed with
, the test for independence between row and column variables can be performed with![]() . Under independence we have, as
. Under independence we have, as![]() ,
, ![]() if
if![]() , and
, and
![]() if
if![]() , where
, where ![]() is the chi-square distribution with
is the chi-square distribution with ![]() d.f. The con-
d.f. The con-
vergence is in law.
To prove this asymptotic result, suppose ![]() a fix value. Let
a fix value. Let![]() . From
. From ![]()
![]() we get
we get
![]() .
.
But![]() . Hence, under independence,
. Hence, under independence, ![]() as
as![]() . Thus
. Thus
![]() .
.
If ![]() then
then ![]() and the above limit reduces to
and the above limit reduces to![]() .
.
5. Correspondence Analysis
In this and the following sections, we present several methods of representation, distinguishing, when it is necessary, the centered from the uncentered solution. The inertia is given by the geometric variability and the generalized Pearson coefficient, respectively.
Centered and Uncentered ![]()
![]() .
.
1) Chi-square distance between rows:![]() .
.
2) Rows and columns coordinates:![]() .
.
3) Inertia:![]() .
.
Some authors considered CA the most rational method for analyzing contingency tables, because its ability to display in a meaningful way the relationships between the categories of two variable [8] -[10] . For the history of CA, see [11] , and for a continuous extension, see [12] [13] . CA can be understood as the first order approxima- tion to the alternatives HD and LR given below [3] . Besides, LR would be a limiting case of parametric CA [14] .
6. Hellinger Distance Analysis
Centered![]() , Uncentered (
, Uncentered (![]()
![]()
1) Hellinger distance between rows:![]() .
.
2) Rows and columns coordinates:![]() .
.
3) Inertia:![]() ,
,
![]() .
.
Although the distances between rows are the same, the principal coordinates in the centered and uncentered
solutions are distinct. Note that ![]() is the so-called affinity coefficient and that
is the so-called affinity coefficient and that![]() .
.
HD is suitable when we are comparing several multinomial populations and the column profiles should not have influence on the distance. See [15] [16] .
7. Non-Symmetric Correspondence Analysis
Centered and Uncentered ![]()
![]() .
.
1) Distance between rows:![]() .
.
2) Rows and columns coordinates:![]() .
.
3) Inertia:![]() .
.
Note that ![]() is related to the Goodman-Kruskal coefficient
is related to the Goodman-Kruskal coefficient ![]() in a contingency table. This measure is
in a contingency table. This measure is
![]() .
.
The numerator of ![]() represents the overall predictability of the columns given the rows. Thus NSCA may be useful when a categorical variable plays the role of response depending on a predictor variable, see [17] -[19] .
represents the overall predictability of the columns given the rows. Thus NSCA may be useful when a categorical variable plays the role of response depending on a predictor variable, see [17] -[19] .
8. Log-Ratio Analysis
Centered![]() , Uncentered
, Uncentered ![]()
![]()
1) Log-ratio distance between rows:![]() .
.
2) Rows and columns coordinates:![]() ,
,![]() .
.
3) Inertia:![]() ,
,
![]() .
.
In spite of having the same distances, the principal coordinates (centered and uncentered) are different. Note that![]() . This method satisfies the principle of subcompositional coherence and is appropriate for positive compositional data [20] .
. This method satisfies the principle of subcompositional coherence and is appropriate for positive compositional data [20] .
The inertia and the geometric variability in these four methods, as well as Taguchi’s method given in Section 2, are summarized in Table 2. For a comparison between CA, HD, and LR see [3] [21] . Besides, by varying the parameters there is the possibility of a dynamic presentation linking these methods [22] .
9. Double-Centered Log-Ratio Analysis
In LR analysis Lewi [23] and Greenacre [4] considered the weighted double-centered solution
![]() ,
,
called “spectral map”. The unweighted double-centered solution, called “variation diagram”, was considered by Aitchison and Greenacre [20] . They show that log-ratio and centered log-ratio biplots are equivalent. In this solution the role of rows and columns is symmetric.
10. Analysis Based on Cumulative Frequencies
Let ![]() be the
be the ![]() contingency table,
contingency table, ![]() and
and ![]() the row and column marginals. Given a row
the row and column marginals. Given a row ![]() let us consider the cumulative frequencies
let us consider the cumulative frequencies
![]() ,
,
and cumulative column proportions
![]() .
.
The Taguchi’s statistic [24] , is given by
![]() ,
,
![]()
Table 2. Inertia expressions for five methods for representing rows in contingency tables. In CA and NSCA the geometric variability coincides with the contingency coefficient. This coefficient does not apply in TA.
where ![]() are weights. Two choices are possible:
are weights. Two choices are possible: ![]() and
and![]() . The test based
. The test based
on ![]() is better than Pearson chi-square when there is an order in the categories of the rows or columns of the contingency table [25] .
is better than Pearson chi-square when there is an order in the categories of the rows or columns of the contingency table [25] .
The so-called Taguchi’s inertia ![]() is
is
![]()
By using ![]() and the
and the ![]() triangular matrix
triangular matrix
![]() ,
,
then ![]() and
and![]() . Thus
. Thus ![]() depends on
depends on ![]() and can be expressed as
and can be expressed as
![]() .
.
As it occurs in CA, where the inertia is the trace ![]() with
with![]() , Beh et al. [26] considered the decomposition of Taguchi’s inertia. In our matrix notation. using the above
, Beh et al. [26] considered the decomposition of Taguchi’s inertia. In our matrix notation. using the above![]() , we have
, we have
![]() .
.
From (4), centering is not necessary here![]() This SVD provides an alternative for visualizing the rows and columns of
This SVD provides an alternative for visualizing the rows and columns of![]() . The main aspects of this solution, where
. The main aspects of this solution, where ![]() is the cumulative sum for row
is the cumulative sum for row ![]() and
and![]() , are:
, are:
1) Distance between rows:![]() .
.
2) Rows and columns coordinates:![]() ,
,![]() .
.
3) Inertia:
![]() ,
,
where![]() .
.
There is a formal analogy between ![]() and the Goodman-Kruskal coefficient
and the Goodman-Kruskal coefficient![]() . Also note that the last column in
. Also note that the last column in ![]() and
and ![]() are equal, so in
are equal, so in ![]() the index
the index ![]() can run from 1 to
can run from 1 to![]() .
.
11. Double Acumulative Frequencies
More generally, the analysis of a contingency table ![]() may also be approached by using cumulative fre- quencies for rows and columns. Thus an approach based on double accumulative (DA) frequencies is
may also be approached by using cumulative fre- quencies for rows and columns. Thus an approach based on double accumulative (DA) frequencies is
![]() ,
,
where ![]() is a suitable triangular matrix with ones. Clearly matrices
is a suitable triangular matrix with ones. Clearly matrices![]() ,
, ![]() ,
, ![]() contain the cumulative frequencies [1] . However, both cumulative approaches TA and DA may not provide a clear display of the contingency table.
contain the cumulative frequencies [1] . However, both cumulative approaches TA and DA may not provide a clear display of the contingency table.
Finally, from
![]() ,
,
all (uncentered) methods CA, HD, NSCA, LR, TA and DA can be unified by means of the SVD
![]() ,
,
as it is reported in Table 3. If![]() , we suppose
, we suppose ![]() in the null entries of
in the null entries of ![]() and
and![]() .
.
12. An Example
The data in Table 4 is well known. This table combines the hair and eye colour of 5383 individuals. We present the first two principal coordinates (centered solution) of the five hair colour categories for CA, HD, LR and NSCA. We multiply the NSCA solution (denoted by![]() ) by 2 for comparison purposes.
) by 2 for comparison purposes.
![]()
These four solutions are similar.
Finally, we show the first two coordinates for Taguchi’s and double accumulative solutions![]() , but multiplying by 3 for comparison purposes.
, but multiplying by 3 for comparison purposes.
![]()
Table 3. Correspondence analysis, Hellinger analysis, non-symmetric correspondence analysis, log-ratio analysis and two solutions based on cumulative frequencies. The right column suggests the type of categorical data.
![]()
Table 4. Classification of a large sample of people combining the hair colour and the eye colour.
![]() .
.
Both solutions are quite distinct from the previous ones.