A Comparison of Statistics for Assessing Model Invariance in Latent Class Analysis ()
1. Introduction
Over the last 20 years, latent class analysis (LCA) has become a very popular statistical method for identifying unobserved groups in the population using multiple observed dichotomous or polytomous outcome variables. A variant of this technique, commonly referred to as latent profile analysis (LPA), can be used to identify latent classes with observed continuous outcomes. LCA is used in both exploratory [1] and confirmatory [2] analyses. In the exploratory case, researchers have no testable a priori hypotheses regarding the nature of the latent classes in the population. It is certainly possible that they would have some expectations as to the number of such classes, but these surmises would not be sufficiently strong to warrant a formal statement of their existence in the form of hypotheses [3] . In contrast, with confirmatory LCA the researcher would typically have hypotheses about the number of latent classes, as well as some characteristics of these classes in the form of absolute or relative response probabilities on the observed variables. They would then test these hypotheses by comparing models with different parameter constraints [4] . Another application of LCA allows for the comparison of latent class solutions across known groups (e.g. gender) within the broader population [2] . For example, Collins and Lanza [5] have demonstrated the application of multiple groups LCA (MGLCA) as a means for comparing patterns of delinquency across different adolescent age groups. Their work demonstrates how MGLCA can be used to assess the invariance of latent class solutions across two or more known subgroups. The primary purpose of this simulation study is to extend their work by comparing the performance of several statistics that have been suggested for use in assessing the null hypothesis of latent class invariance across multiple known groups.
1.1. The LCA Model
The basic LCA model is described in some detail by McCutcheon [2] . Assume that data have been collected for four observed, dichotomous variables, X1, X2, X3, and X4, and that there exists a latent categorical variable Y, which accounts for the relationships among these four observed variables. The LCA model linking the latent and observed variables can then be expressed as:
 (1)
(1)
where
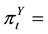 Probability that a randomly selected individual will in latent class cof latent variable
Probability that a randomly selected individual will in latent class cof latent variable ;
;
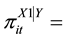 Probability that a member of latent class
Probability that a member of latent class  will provide a response of
will provide a response of  for variable X1;
for variable X1;
 Probability that a member of latent class
Probability that a member of latent class  will provide a response of
will provide a response of 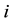 for variable X2;
for variable X2;
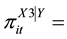 Probability that a member of latent class
Probability that a member of latent class  will provide a response of
will provide a response of  for variable X3;
for variable X3;
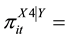 Probability that a member of latent class
Probability that a member of latent class 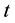 will provide a response of
will provide a response of 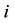 for variable X4.
for variable X4.
As an example of how these parameters are interpreted, take an individual from the population who has the following probability values for the three classes in Y: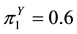 ,
, ![]() , and
, and![]() . These results indicate that the individual is most likely a member of class 1 of the latent variable, with only a 1/4 chance of being in class 2 and a less than 1/5 chance of being in class 3. In addition, assume that observed variable X1 is a survey item asking whether an individual never uses sunscreen when they go outside for extended periods of time. A value for
. These results indicate that the individual is most likely a member of class 1 of the latent variable, with only a 1/4 chance of being in class 2 and a less than 1/5 chance of being in class 3. In addition, assume that observed variable X1 is a survey item asking whether an individual never uses sunscreen when they go outside for extended periods of time. A value for ![]() of 0.25 would indicate that an individual in the first class of the latent variable would have a fairly low likelihood of responding Yes to this item; i.e. most members of latent class 1 do use sunscreen when spending extended periods of time outside.
of 0.25 would indicate that an individual in the first class of the latent variable would have a fairly low likelihood of responding Yes to this item; i.e. most members of latent class 1 do use sunscreen when spending extended periods of time outside.
1.2. MG LCA and Invariance Testing
As mentioned earlier, in some instances a researcher may be interested in ascertaining whether the nature of latent classes differs across known subgroups in the populations. For example, psychologists studying risk taking behavior among adolescents may have theoretical reasons to believe that in the broad teen aged population there are a relatively small number of latent classes with specific risk taking profiles. Further, it may be hypothesized that these classes differ for males and females, either in terms of their relative frequency, their item response profiles or both. In this context, the researcher would like to determine 1) whether indeed coherent latent classes of youth exist based on risk taking behavior, and if so, 2) whether these classes differ for males and females. It is for this type of problem that MGLCA is appropriate.
Collins and Lanza [5] provide an excellent and detailed discussion of invariance testing using MGLCA. There- fore, this manuscript contains only a summary of the methodology, and the interested reader who would like more detail is referred to [5] . The MGLCA model is simply an extension of the original LCA model in (1):
![]() (2)
(2)
where all terms are as defined previously and the new term G ![]() refers to observed group membership (e.g. gender). In other words, latent class prevalence and item response probabilities are conditional on group membership, thus allowing for the possibility of differences across the groups.
refers to observed group membership (e.g. gender). In other words, latent class prevalence and item response probabilities are conditional on group membership, thus allowing for the possibility of differences across the groups.
The researcher interested in group invariance for the LCA models will want to assess whether the number of latent classes, the class specific item response probabilities and the prevalence of the classes are the same across the known groups of interest. Typically LCA invariance testing begins by determining the number of latent classes in the population as a whole, followed by a determination as to whether the number is the same in each group. This stage of the analysis is very akin to assessing configural invariance in the factor analysis context, where no equality constraints are placed on parameters, and only the groups’ factor patterns are compared using exploratory factor analysis. Similarly, in LCA the researcher would determine whether the number of latent classes is the same across groups, using exploratory LCA with each group independently. This is typically done by fitting LCA models to the groups separately and using standard methods for determining the number of latent classes in each. Selecting the optimal model for a given dataset is typically done using one or more goodness of fit statistics [6] .
If it has been determined that the number of latent classes is equivalent across groups, the researcher may then go on to assess whether item response probabilities are also equal across groups. This stage of LCA invariance assessment corresponds loosely to measurement invariance assessment in factor analysis, forming the second step in the process. In factor analysis, measurement invariance involves the determination as to whether factor loadings are equivalent across groups, while measurement invariance in LCA refers to whether performance on the observed indicators (e.g. probability of endorsing an item) is equivalent across groups. However, if the num- ber of classes differs across groups, no further invariance assessment should be conducted [5] . With factor analysis, a lack of measurement invariance (i.e. group differences in factor loadings) means that the factors themselves have a different interpretation across the groups. Similarly, in the context of LCA a lack of measurement invariance indicates that the nature of the latent classes differs across the groups. If the classes have different response probabilities for one or more indicator variables across the known groups, then the meaning of the classes differs across the groups as well, and so must the interpretation of them. In such a case, researchers cannot describe the population as consisting of a set number of latent classes with common traits, but rather must think of the classes as being fundamentally different in nature depending on one’s membership in a given known group.
In order to determine whether the latent class specific response probabilities are invariant across groups, the researcher would fit two models to the data. In the first model all response probabilities are allowed to vary across groups, while in the second model these probabilities are constrained to be equal. Using the example described previously, in the second model the response probability for variable X1 for latent class 1 is constrained to be the same for both groups, as are the response probabilities for item X1 in latent class 2, item X2 in latent class 1 and so on. The fit of the two models to the data is then compared using one or more of the statistical techniques described below. If the constrained model provides a substantially worse fit than the unconstrained, the researcher would conclude that the groups differ in terms of one or more of the latent class specific item response probabilities. As an example, the researcher interested in comparing latent classes based on risk behavior across genders would first fit a model in which all of the latent class specific item response probabilities were free to vary between males and females, and then a second model in which they were constrained to be equal for the two groups. She would then compare the fit of the two models to determine whether the LCA model for risk was invariant across genders.
If the number of latent classes and the item response probabilities are both determined to be invariant across groups, the researcher can test for the invariance of class prevalence. In other words, she will assess whether the relative size of each latent class is the same across the observed groups. This third stage in the invariance testing methodology is analogous to testing for metric invariance in factor analysis, in that we are interested in the extent to which the mean group prevalence is the same across groups, in the same way that we are interested in whether indicator intercepts are group equivalent with metric invariance. Comparing the equivalence of class prevalence across groups is done in much the same manner as assessing response probability invariance: A model constraining response probabilities and allowing prevalence rates to vary is fit to the data, and its fit is compared to that of the fully constrained model. If the constrained model provides substantially worse fit than that of the unconstrained prevalence model, then the researcher would conclude that class prevalence rates are not invariant across groups.
1.3. Statistics Used in Assessing LCA Model Invariance
As described above, the process of assessing LCA model invariance involves the comparison of fit for a fully constrained and several unconstrained models. This comparison of relative fit is key to the success of the entire invariance testing venture, and thus is of some importance to researchers interested in this type of analysis. A number of statistical tools have been suggested for use in the assessment of LCA invariance, including the likelihood ratio test, as well as a variety of information indices. However, there has been little research focused on the relative performance of these statistics in terms of making accurate determinations regarding the presence (or absence) of LCA model invariance. Therefore, as mentioned previously, the primary focus of this study is on the systematic comparison of these statistical techniques in order to ascertain which might be most accurate in the context of LCA invariance assessment, both in terms of correctly identifying when invariance is not present, as well as when it is.
The statistics to be examined in this study can be divided into three broad classes: a chi-square difference test, information indices, and a parametric bootstrap test. The first of these is based on the likelihood ratio statistic, ![]() , which is a measure of absolute fit in the single group LCA context, and can be used to construct a test of invariance in the multiple groups situation. With a single group,
, which is a measure of absolute fit in the single group LCA context, and can be used to construct a test of invariance in the multiple groups situation. With a single group, ![]() tests the null hypothesis that the proposed latent class solution adequately fits the observed data, and can be expressed as
tests the null hypothesis that the proposed latent class solution adequately fits the observed data, and can be expressed as
![]() (3)
(3)
where
![]()
![]()
The ![]() statistic essentially compares the actual counts in each of the
statistic essentially compares the actual counts in each of the ![]() cells created by the set of categorical indicator variables with the cell counts predicted by the model. The further the predicted counts are from the actual, the greater value of the test statistic and the more evidence exists that the proposed model does not fit the observed data. The degrees of freedom for this test are W-P-1, where W is the total number of cells obtained from the cross- tabulation of the observed variables, and P is the number of parameters estimated by the model.
cells created by the set of categorical indicator variables with the cell counts predicted by the model. The further the predicted counts are from the actual, the greater value of the test statistic and the more evidence exists that the proposed model does not fit the observed data. The degrees of freedom for this test are W-P-1, where W is the total number of cells obtained from the cross- tabulation of the observed variables, and P is the number of parameters estimated by the model. ![]() can be compared to the
can be compared to the ![]() distribution with W-P-1 degrees of freedom under certain conditions. This test statistic relies on the assumption of multivariate normality of the observed indicator variables, which is not often met in practice, in which case the
distribution with W-P-1 degrees of freedom under certain conditions. This test statistic relies on the assumption of multivariate normality of the observed indicator variables, which is not often met in practice, in which case the ![]() may not be a reliable indicator of model fit [2] [6] .
may not be a reliable indicator of model fit [2] [6] .
In the context of multiple groups LCA, which is the focus of this study, the difference of ![]() statistics can be used to assess the null hypothesis of LCA parameter invariance. For example, consider the case in which we are interested in assessing the measurement invariance of a LCA solution across two groups. Two models would need to be fit to the data, the first allowing item parameter values to vary across the two groups, and the second constraining these parameters to be equal across the groups. The relative fit of these two models can then be compared using the difference between their
statistics can be used to assess the null hypothesis of LCA parameter invariance. For example, consider the case in which we are interested in assessing the measurement invariance of a LCA solution across two groups. Two models would need to be fit to the data, the first allowing item parameter values to vary across the two groups, and the second constraining these parameters to be equal across the groups. The relative fit of these two models can then be compared using the difference between their ![]() values. This
values. This ![]() statistic is asymptotically distributed as a
statistic is asymptotically distributed as a ![]() with
with![]() . A statistically significant result for this test would indicate that the fit of the two models differed; i.e. constraining the model parameters to be equal between the groups resulted in worse model fit than allowing them to vary [5] . This strategy is very similar to that for testing the fit of two structural equation models. Indeed, the use of the
. A statistically significant result for this test would indicate that the fit of the two models differed; i.e. constraining the model parameters to be equal between the groups resulted in worse model fit than allowing them to vary [5] . This strategy is very similar to that for testing the fit of two structural equation models. Indeed, the use of the ![]() difference test for invariance assessment in the context of structural equation modeling (SEM) has been studied by a number of researchers and found to be an effective tool for accurately identifying the presence of noninvariance in many situations [7] -[9] .
difference test for invariance assessment in the context of structural equation modeling (SEM) has been studied by a number of researchers and found to be an effective tool for accurately identifying the presence of noninvariance in many situations [7] -[9] .
An alternative approach to assessing invariance using the ![]() test involves a class of statistics known collectively as information criteria (IC). These IC’s are all based on the log-likelihood of a given model, each applying a different penalty for model complexity. The smaller the value of an IC, the better fitting the model is said to be. In the context of LCA, several such criteria are used to assess model fit, including the Akaike Information Criterion (AIC), the consistent AIC (CAIC), the Bayesian Information Criterion (BIC), and the sample size adjusted BIC (aBIC). The AIC is calculated as:
test involves a class of statistics known collectively as information criteria (IC). These IC’s are all based on the log-likelihood of a given model, each applying a different penalty for model complexity. The smaller the value of an IC, the better fitting the model is said to be. In the context of LCA, several such criteria are used to assess model fit, including the Akaike Information Criterion (AIC), the consistent AIC (CAIC), the Bayesian Information Criterion (BIC), and the sample size adjusted BIC (aBIC). The AIC is calculated as:
![]() (4)
(4)
where
![]() is the log likelihood for the model, and
is the log likelihood for the model, and ![]() is the number of estimated model parameters [10] . Thus, holding the value of
is the number of estimated model parameters [10] . Thus, holding the value of ![]() constant, models with more parameters will have larger values of AIC. An alternative to the AIC, which includes both the number of model parameters and the sample size
constant, models with more parameters will have larger values of AIC. An alternative to the AIC, which includes both the number of model parameters and the sample size ![]() in the penalty term is the CAIC [11] .
in the penalty term is the CAIC [11] .
![]() (5)
(5)
The BIC takes a similar form to the CAIC, and is calculated as:
![]() (6)
(6)
Finally, the aBIC (Sclove, 1987) involves an adjusted sample size value.
![]() (7)
(7)
where
![]()
A third general approach for assessing the relative fit of the constrained and unconstrained models that will be investigated here is based upon the parametric bootstrap likelihood ratio test that has been shown effective for identifying the correct number of classes in LCA [12] . When applied to the problem of identifying the correct number of classes for standard one group LCA, this methodology involves the estimation of the distribution of the difference in ![]() values when comparing models that differ in terms of the number of latent classes. In other words, a researcher interested in comparing the fit of k and
values when comparing models that differ in terms of the number of latent classes. In other words, a researcher interested in comparing the fit of k and ![]() latent classes would use the BLRT to obtain a p-value that could be used to determine whether the fit was significantly different between models for the two numbers of latent classes. A primary advantage of this approach is that it does not rely on assumptions regarding the distribution of the difference in
latent classes would use the BLRT to obtain a p-value that could be used to determine whether the fit was significantly different between models for the two numbers of latent classes. A primary advantage of this approach is that it does not rely on assumptions regarding the distribution of the difference in ![]() values for the k and
values for the k and ![]() models [12] .
models [12] .
In the current application, the BLRT was used to assess the difference in fit for the constrained and unconstrained models described above. The basic methodology is very similar to that outlined in [6] , in the following steps:
1) Estimate the constrained and unconstrained models, and obtain the ![]() values for each.
values for each.
2) Under the null model that invariance holds (i.e. the constrained model), generate a bootstrap sample and calculate the difference in ![]() values
values ![]() for the constrained and unconstrained models.
for the constrained and unconstrained models.
3) Repeat step 2 B (e.g. 1000) times in order to obtain the distribution of ![]() when the null hypothesis of invariance holds.
when the null hypothesis of invariance holds.
4) Obtain the p-value testing the invariance hypothesis by comparing the actual ![]() statistic with the distribution from step 3. If the observed value is greater than or equal to the 95th percentile of the distribution, then reject the null hypothesis of model invariance. The BLRT can be applied to the testing of both measurement invariance, and the equivalence of class prevalences across groups.
statistic with the distribution from step 3. If the observed value is greater than or equal to the 95th percentile of the distribution, then reject the null hypothesis of model invariance. The BLRT can be applied to the testing of both measurement invariance, and the equivalence of class prevalences across groups.
1.4. Prior Research in LCA Model Selection and Model Invariance Assessment
While, as mentioned previously, there has been relatively little work in assessing the performance of statistics for testing model invariance in the context of LCA, research has been conducted investigating methods for invariance assessment of structural equation models, and comparing approaches for identifying optimal LCA models. These studies provide insights into the broader questions of invariance assessment and LCA model selection, and will therefore be reviewed here.
With regard to the selection of the optimal number of classes in various types of mixture models, researchers have compared a number of methods, including information indices such as the AIC, BIC, and aBIC, along with hypothesis tests including the ![]() test, and the BLRT. These earlier studies generally found that among the information indices, the aBIC was optimal for correctly selecting the number of latent classes for growth mixture models [13] , and for latent class models [14] . Other research has found that the AIC can lead to overestimation of the number of latent classes [15] , while the BIC provides reasonably accurate determination as to the number of classes [16] . In terms of hypothesis tests, research has revealed that for small samples or a large number of indicator variables, the
test, and the BLRT. These earlier studies generally found that among the information indices, the aBIC was optimal for correctly selecting the number of latent classes for growth mixture models [13] , and for latent class models [14] . Other research has found that the AIC can lead to overestimation of the number of latent classes [15] , while the BIC provides reasonably accurate determination as to the number of classes [16] . In terms of hypothesis tests, research has revealed that for small samples or a large number of indicator variables, the ![]() test tends to overestimate the number of classes, because the underlying distribution of
test tends to overestimate the number of classes, because the underlying distribution of ![]() difference values does not follow the chi-square [17] -[19] . Further work in this area [6] replicated this overestimation problem for the
difference values does not follow the chi-square [17] -[19] . Further work in this area [6] replicated this overestimation problem for the ![]() test. In addition, their results showed that the BLRT was able to maintain the nominal Type I error rate, while yielding optimal power for identifying the correct number of latent classes. Nylund et al. [6] also found that the aBIC was consistently the most accurate of the information indices in terms of identifying the correct number of latent classes when the indicator variables were categorical, as is the case in the current study, and that the CAIC was less likely than the AIC to overestimate the number of classes. Finally, when considering all statistical methods for determining the number of latent classes, Nylund et al. concluded that the BLRT was the optimal method for LCA model selection, overall, even when compared to the aBIC. Thus, one goal of the current study was to ascertain whether this approach would also be effective for the problem of model invariance assessment.
test. In addition, their results showed that the BLRT was able to maintain the nominal Type I error rate, while yielding optimal power for identifying the correct number of latent classes. Nylund et al. [6] also found that the aBIC was consistently the most accurate of the information indices in terms of identifying the correct number of latent classes when the indicator variables were categorical, as is the case in the current study, and that the CAIC was less likely than the AIC to overestimate the number of classes. Finally, when considering all statistical methods for determining the number of latent classes, Nylund et al. concluded that the BLRT was the optimal method for LCA model selection, overall, even when compared to the aBIC. Thus, one goal of the current study was to ascertain whether this approach would also be effective for the problem of model invariance assessment.
The literature on invariance testing for structural equation modeling (SEM) has also focused on the use of both hypothesis testing and information indices. For example, French and Finch [7] found that when indicator variables were normally distributed continuous variables, the ![]() test exhibited good control of the Type I error rate when testing for measurement invariance (group differences in loadings), while at the same time yielding relatively high power for identifying a lack of invariance. However, when the indicators were dichotomous, they found that this test generally had very low power across sample sizes. Meade, and Lautenschlager [20] reported that with large samples (2000 or more), the
test exhibited good control of the Type I error rate when testing for measurement invariance (group differences in loadings), while at the same time yielding relatively high power for identifying a lack of invariance. However, when the indicators were dichotomous, they found that this test generally had very low power across sample sizes. Meade, and Lautenschlager [20] reported that with large samples (2000 or more), the ![]() test had high power for detecting even minor differences in the constrained and unconstrained models, leading to findings of noninvariance for very small actual differences in parameters across groups. With respect to information indices and SEM invariance assessment, Burnham and Anderson [21] suggested use of the CAIC over the AIC when the ratio of sample size to number of parameters was less than 40, similar to the results reported in Nylund et al. in the context of LCA. On the other hand, Vrieze [22] concluded that for complex latent variable models, the AIC may be the preferable approach because of its particular min-max properties not shared by other information indices, such as the BIC. In a similar vein, Shao [23] suggested that AIC is preferable to BIC when the true model in the population is very complex, which he argued is probably most often the case in practice. Focusing specifically on factor invariance assessment with information indices, Wicherts and Dolan [24] reported that these indices can be very useful for selecting between constrained and unconstrained models, as long as researchers are careful to ensure that the two models are identical with the exception of the parameters being tested. They noted that when this is not the case, invariance assessment will be compromised. In short, while there has been much work investigating approaches for model invariance assessment in SEM, the results have not produced a clearly optimal approach, unlike the BLRT for LCA model selection. The
test had high power for detecting even minor differences in the constrained and unconstrained models, leading to findings of noninvariance for very small actual differences in parameters across groups. With respect to information indices and SEM invariance assessment, Burnham and Anderson [21] suggested use of the CAIC over the AIC when the ratio of sample size to number of parameters was less than 40, similar to the results reported in Nylund et al. in the context of LCA. On the other hand, Vrieze [22] concluded that for complex latent variable models, the AIC may be the preferable approach because of its particular min-max properties not shared by other information indices, such as the BIC. In a similar vein, Shao [23] suggested that AIC is preferable to BIC when the true model in the population is very complex, which he argued is probably most often the case in practice. Focusing specifically on factor invariance assessment with information indices, Wicherts and Dolan [24] reported that these indices can be very useful for selecting between constrained and unconstrained models, as long as researchers are careful to ensure that the two models are identical with the exception of the parameters being tested. They noted that when this is not the case, invariance assessment will be compromised. In short, while there has been much work investigating approaches for model invariance assessment in SEM, the results have not produced a clearly optimal approach, unlike the BLRT for LCA model selection. The ![]() test was not effective for categorical indicator variables, which are common in LCA, and no single information index consistently performed the best for SEM invariance assessment. Thus, it is hoped that the current work may expand this literature by both investigating the performance of these traditional methods of invariance assessment in the context of LCA, rather than SEM, and by comparing them with BLRT, which has heretofore been used for LCA model selection rather than invariance testing.
test was not effective for categorical indicator variables, which are common in LCA, and no single information index consistently performed the best for SEM invariance assessment. Thus, it is hoped that the current work may expand this literature by both investigating the performance of these traditional methods of invariance assessment in the context of LCA, rather than SEM, and by comparing them with BLRT, which has heretofore been used for LCA model selection rather than invariance testing.
1.5. Goal of the Current Study
The primary goal of the current study was to compare the performance of a variety of statistical approaches for assessing group invariance in the context of LCA. While much prior work has been done comparing methods for assessing overall model fit in the context of LCA, there is very little published research comparing statistics for assessing latent class model invariance across multiple known groups. In addition, while these statistics are all familiar parts of the statistics landscape and have been studied in other modeling contexts, they have not been examined in terms of their abilities to accurately assess latent class invariance. Therefore, these methods, including the ![]() test, BLRT, AIC, BIC, CAIC and aBIC, were used to check for the presence of measurement invariance and to compare class prevalences across two known groups, under a variety of simulated conditions. Based on the prior literature that is described above, it is hypothesized that the BLRT will generally perform well, given its aforementioned strength in correctly identifying the number of latent classes in the population. It is also anticipated that, given prior work demonstrating its sensitivity to both non-normality and sample size, the
test, BLRT, AIC, BIC, CAIC and aBIC, were used to check for the presence of measurement invariance and to compare class prevalences across two known groups, under a variety of simulated conditions. Based on the prior literature that is described above, it is hypothesized that the BLRT will generally perform well, given its aforementioned strength in correctly identifying the number of latent classes in the population. It is also anticipated that, given prior work demonstrating its sensitivity to both non-normality and sample size, the ![]() test will have difficulty with the invariance problem studied here, given the nonnormal (dichotomous) nature of the indicator variables, and the variety of sample sizes studied. Finally, as Collins and Lanza [5] have noted, the information indices may be better suited to narrowing down the list of possible optimal models rather than identifying a single best model. Among these statistics, prior studies provide some evidence that the aBIC may be a top choice, but much of the work supporting this hypothesis has been limited to the continuous indicator case. In sum, as has been noted in earlier writing [21] [22] , more work needs to be done investigating the relative performance of a number of model selection tools in the context of mixture models, including LCA invariance assessment. In addition to using a simulation approach to compare the performance of invariance testing statistics under a variety of conditions, a secondary goal of this study was to demonstrate the practice of invariance assessment using MGLCA with data taken from the Youth Risk Behavior Survey (YRBS). The results of both the simulation and applied data analysis should serve to inform both practitioners and researchers regarding the use of MGLCA for invariance assessment, and should further work in the area of LCA invariance assessment.
test will have difficulty with the invariance problem studied here, given the nonnormal (dichotomous) nature of the indicator variables, and the variety of sample sizes studied. Finally, as Collins and Lanza [5] have noted, the information indices may be better suited to narrowing down the list of possible optimal models rather than identifying a single best model. Among these statistics, prior studies provide some evidence that the aBIC may be a top choice, but much of the work supporting this hypothesis has been limited to the continuous indicator case. In sum, as has been noted in earlier writing [21] [22] , more work needs to be done investigating the relative performance of a number of model selection tools in the context of mixture models, including LCA invariance assessment. In addition to using a simulation approach to compare the performance of invariance testing statistics under a variety of conditions, a secondary goal of this study was to demonstrate the practice of invariance assessment using MGLCA with data taken from the Youth Risk Behavior Survey (YRBS). The results of both the simulation and applied data analysis should serve to inform both practitioners and researchers regarding the use of MGLCA for invariance assessment, and should further work in the area of LCA invariance assessment.
2. Methods
Data for this Monte Carlo study were generated using the Simulate Lca Dataset SAS macro, version 1.1.0 [25] , while data were analyzed using PROC LCA [26] under the SAS version 9.1 system [27] . All manipulated factors, which are described in detail below, were crossed such that there were 6 (latent class assessment procedure) × 2 (type of invariance) × 2 (number of latent classes) × 4 (sample size) × 2 (observed group size ratio) × 2 (latent class size ratio) × 3 (proportion of noninvariant items) × 4 (degree of noninvariance across groups) combinations, for a total of 4608 individual study conditions. For each combination of conditions, 1000 simulation replications were generated and analyzed. As mentioned previously, the approaches to invariance assessment included in this study were the ![]() test, BLRT, AIC, BIC, CAIC and aBIC. The manipulated simulation conditions, each of which is described in detail below, were based upon data reported in Collins and Lanza [5] , chapter 5. For all of the conditions, 2 groups were simulated with 5 dichotomous indicator variables. The data were simulated using the pattern of item endorsement probabilities that appear in Table 1. Note that these values were identical for the two observed groups in the invariant condition, while they changed for group 2 in the noninvariant cases, as described below. For the 2 latent class conditions only the item endorsement probabilities in the first two columns of Table 1 were used.
test, BLRT, AIC, BIC, CAIC and aBIC. The manipulated simulation conditions, each of which is described in detail below, were based upon data reported in Collins and Lanza [5] , chapter 5. For all of the conditions, 2 groups were simulated with 5 dichotomous indicator variables. The data were simulated using the pattern of item endorsement probabilities that appear in Table 1. Note that these values were identical for the two observed groups in the invariant condition, while they changed for group 2 in the noninvariant cases, as described below. For the 2 latent class conditions only the item endorsement probabilities in the first two columns of Table 1 were used.
2.1. Manipulated Study Conditions
Type of Invariance
Two types of invariance were assessed in this study. Measurement invariance involved testing whether the latent class specific item response probabilities were the same between the two known groups. In addition, thee quivalence of the relative frequencies of the latent classes in each group was also tested. Based upon recommendations in Collins and Lanza [5] , the equality of the latent class prevalences across groups was tested under the assumption of strict measurement invariance. Thus, item response probabilities for the latent classes were simulated to be the same across groups when latent class prevalences were compared.
2.2. Number of Latent Classes
Data were simulated with either 2 or 4 latent classes in each observed group for the measurement invariance analysis. For testing the equivalence of class prevalence, 2 latent classes were simulated for each observed group, in order to allow for focus on the basic test of invariance without the complicating presence of multiple groups. For all simulation conditions, each group contained the same number of latent classes. It is recognized that in actual practice the number of latent classes will not always be the same for multiple groups in such an invariance study, making this design decision a limitation of the current study. However, this decision was made for two reasons. First, this simulation setup reflects the case where the first level of invariance has been met, namely that the number of groups in the latent classes is identical. Were this condition not to hold, further invariance testing would not be conducted, as the researcher would presumably have discovered that the number of classes differed
![]()
Table 1. Endorsement probabilities used to simulate data, by item and latent class.
across groups when he fit the LCA models separately for them. The second reason for this design condition is to keep the size of the study and number of conditions manageable. Nonetheless, it is certainly true that keeping the number of classes constant for the two groups does not reflect every condition that a researcher might see in practice, and is therefore a limitation of the current study.
2.3. Sample Size and Observed Group Size Ratio
Four total sample size conditions were simulated, including 200, 500, 1000 and 2000, which were designed to represent a range of values that appear in the applied literature in which LCA is used. Two observed group size ratio conditions were also simulated: 1/1 and 3/1.
2.4. Latent Class Size Ratio
For the measurement invariance aspect of the study, the ratio of latent classes within each group were simulated to be either 50/50 or 70/30 in the 2 latent classes condition. In the 4 class case, the ratios were either 25/25/25/25 or 55/15/15/15. In the results section below, we will refer to the equal ratio condition as 50/50 for both 2 and 4 latent classes, and the unequal ratio condition as 70/30 for both numbers of latent classes. We recognize that there are many other possible latent class ratios that could be included. However, in order to keep the size of the study manageable we have elected to examine only these conditions. For the portion of the study examining latent class prevalence, the latent class ratios were manipulated as described in the Degree of noninvariance section below.
2.5. Proportion of Noninvariant Items
For the measurement invariance aspect of the study, 3 conditions for proportion of noninvariant items were simulated, including 0% (complete invariance), 20% (1 target item) and 40% (2 target items).
2.6. Magnitude of Measurement Noninvariance
The magnitude of noninvariance present in the target items was based loosely on results regarding adolescent delinquency reported in Collins and Lanza [5] . The magnitude of noninvariance between the observed groupslatent class specific item response probabilities for target items were set to 0 (complete invariance corresponding to the 0% proportion of invariant item condition described above), 0.1, 0.3 or 0.5. An example of how these noninvariant data were simulated appears in Table 2 for the 2 observed groups, 2 latent classes, 20% noninvariant condition, for each degree of measurement noninvariance (i.e. 0, 0.1, 0.3, and 0.5). Consider as an example the noninvariance = 0 magnitude case, which is represented in the top section of Table 2. For all conditions simulated here, the target parameter is the probability of endorsing item 1, which appears in bold. Here, the latent class endorsement probabilities were identical for the two observed groups across the 5 items, as seen in Table 2. The noninvariance = 0.1 case with 20% noninvariant items appears in the second section of Table 2. In this case, latent class 1 in observed group 1 was simulated to have a proportion endorsing the dichotomous item of 0.8, while latent class 1 in observed group 2 was simulated to endorse the item at a rate of 0.7. Similarly, as seen in the third section of Table 2, for noninvariance = 0.3, latent class 1 in observed group 1 was simulated to have an endorsement probability for item 1 of 0.8, while latent class 1 in observed group 2 was simulated to have an endorsement probability of 0.5. A similar design was used for all other conditions included in this study.
2.7. Magnitude of Class Prevalence Inequality
In terms of latent class prevalence equivalence assessment, group 1 always had an equal distribution of latent class membership; i.e. 0.5/0.5 for 2 classes and 0.25/0.25/0.25/0.25 for 4 classes. Latent class prevalence rates then differed from group 2 by 0.05, 0.1, 0.15 or 0.3. Thus, for example, in the 0.3 prevalence difference condition, latent class 1 in group 1 was simulated to appear in 50% (0.5) of cases, while for group 2 latent class 1 was simulated to appear in 80% (0.8) of cases.
2.8. Study Outcome Variables
The outcome variables of interest were the Type I error rate (proportion of times noninvariance was indicated by
![]()
Table 2. Example of measurement noninvariance simulation probabilities used to simulate data, by degree of measurement invariance, for the two group, 20% noninvariant condition, 2 latent classes condition.
*Parameter that is simulated to be noninvariant is in bold.
a statistical procedure when data were simulated to be invariant in the population), and power (proportion of times noninvariance was correctly indicated by a statistical procedure when noninvariance was simulated in the data). The nominal Type I error rate set in this study is 0.05. It should be noted that with regard to the information indices, Type I error rate is a misnomer in that these statistics are not hypothesis tests, but rather methods of assessing relative model fit. However, for the sake of ease in reporting results consistently for all of the statistics studied here, this phrase will be applied to all of the methods included in this study. The use of information indices here was in keeping with standard practice, such that they were calculated for the constrained and unconstrained models and then compared with one another. The model with the lower value was taken to be the best fitting in the sample, and this result was compared with the actual state of affairs in the population. If the unconstrained (noninvariant) model was identified as better fitting than the constrained (invariant) model, then the conclusion based on the sample was that the latent class solutions were not invariant across the two known groups. When this decision was in error (i.e. the data were simulated to be invariant), the result was termed a Type I error, though in fact no hypothesis testing was conducted. However, in order to keep reporting of the results as clear and straightforward as possible, the terms Type I error rate and power will be used to signify incorrect and correct determinations of noninvariance. All such invariance testing was done under the assumption that the latent class models were properly specified for each of the observed groups.
2.9. Analysis of Study Outcomes
In order to determine which of the manipulated conditions or their interactions were significantly related to the Type I error and power rates, repeated measures analysis of variance (ANOVA) was used where the rates across all 1000 replications served as the dependent variable, the statistic used to assess invariance was the within subjects factor, and the following manipulated conditions were between subjects factors.
3. Results
The results presented below are divided into evaluations of Type I error and power rates for measurement invariance, and prevalence equivalence, respectively. For measurement invariance, the key points of interest were the comparative Type I error and power rates of the various methods across the levels of noninvariance, and whether any differences in these rates across the invariance testing methods interacted with the other manipulated conditions. Similarly, with respect to assessing the relative prevalence of the two latent classes, primary interest was on comparing the Type I error and power rates of the invariance testing methods, and how those rates changed with increasing differences in the prevalences of the latent classes across the observed groups. In addition, it was of interest to ascertain whether any such differences between the statistics’ performance interacted with other manipulated factors in the study.
3.1. Measurement Invariance: Type I Error Rate
For the ANOVA for measurement invariance Type I error rate, the outcome was the rate of significant group difference findings for each replication when no group differences were simulated. The independent variables were method of invariance testing (method), number of latent classes (classes), class size ratio (classratio), group size ratio (group ratio), and sample size![]() . The results of these analyses indicated that the only significant term was the interaction of method by classes by N
. The results of these analyses indicated that the only significant term was the interaction of method by classes by N![]() . Figure 1 includes Type I error rates for method by classes by N. Of primary interest were the Type I error rates of the methods, for which, across conditions, the BIC, CAIC and aBIC demonstrated rejection rates of 0, except for aBIC with 2 classes and N of 200. In addition, AIC never had rejection rates greater than 0.05 for any of the simulated conditions. On the other hand, the
. Figure 1 includes Type I error rates for method by classes by N. Of primary interest were the Type I error rates of the methods, for which, across conditions, the BIC, CAIC and aBIC demonstrated rejection rates of 0, except for aBIC with 2 classes and N of 200. In addition, AIC never had rejection rates greater than 0.05 for any of the simulated conditions. On the other hand, the ![]() and BLRT tests had rates between 0.05 and 0.075 for 2 classes, whereas with 4 classes and Nof 2000
and BLRT tests had rates between 0.05 and 0.075 for 2 classes, whereas with 4 classes and Nof 2000![]() had an inflated rate of 0.13, while BLRT maintained an error rate below 0.05.
had an inflated rate of 0.13, while BLRT maintained an error rate below 0.05.
3.2. Measurement Invariance: Power
For measurement invariance power, the 3-way interaction of method by N by magnitude of noninvariance (magnitude) was statistically significant![]() , as was the 3-way interaction of method by classes by group ratio
, as was the 3-way interaction of method by classes by group ratio![]() . Table 3 contains the power rates for the 6 methods by magnitude of difference and N. When interpreting these results, it is important to note that the
. Table 3 contains the power rates for the 6 methods by magnitude of difference and N. When interpreting these results, it is important to note that the ![]() test was found to have inflated Type I error rates for
test was found to have inflated Type I error rates for ![]() and classes = 2000, as reported above. In terms of power, of primary interest were the relative performances of the various statistics for assessing invariance. Among these, BLRT displayed the highest power rates across conditions, while the
and classes = 2000, as reported above. In terms of power, of primary interest were the relative performances of the various statistics for assessing invariance. Among these, BLRT displayed the highest power rates across conditions, while the ![]() test consistently yielded the second highest power. The BIC, CAIC, and aBIC all had power values much lower than the other three methods across all conditions, with rates at or near 0 when the groups differed by 0.1.
test consistently yielded the second highest power. The BIC, CAIC, and aBIC all had power values much lower than the other three methods across all conditions, with rates at or near 0 when the groups differed by 0.1.
Table 4 includes the power rates for method by classes by group ratio, the other significant interaction identified using ANOVA. An examination of the results reveals that for all of the methods power with 2 groups was
![]()
Figure 1. Type I error rate for measurement invariance testing by testing method, number of classes and sample size (N).
![]()
Table 3. Power for measurement invariance testing by testing method, magnitude of difference between groups (D), and sample size (N).
![]()
Table 4. Power for measurement invariance testing by method, number of latent classes, and group ratio.
slightly higher when the group ratios were equal, and the BLRT, ![]() test and AIC had higher rates than the other approaches. When 4 classes were present, all of the methods displayed lower power than for 2 classes. In addition, the BLRT had higher power rates than any of the other methods, and both
test and AIC had higher rates than the other approaches. When 4 classes were present, all of the methods displayed lower power than for 2 classes. In addition, the BLRT had higher power rates than any of the other methods, and both ![]() and AIC demonstrated approximately twice as much power when the groups were of equal size as when they were unequal. Finally, BIC, CAIC and aBIC all had power rates at or near 0 for 4 latent classes.
and AIC demonstrated approximately twice as much power when the groups were of equal size as when they were unequal. Finally, BIC, CAIC and aBIC all had power rates at or near 0 for 4 latent classes.
3.3. Measurement Invariance Summary
To summarize the measurement invariance results presented above, all of the methods studied here maintained the nominal Type I error rate of 0.05, except for the ![]() test with a sample size of 2000 and 4 latent classes present in the data. In terms of power, the BLRT yielded the highest rates across conditions, followed by the
test with a sample size of 2000 and 4 latent classes present in the data. In terms of power, the BLRT yielded the highest rates across conditions, followed by the ![]() test and AIC. The BIC, CAIC, and aBIC all yielded much lower power than the other three methods. Furthermore, all of the methods studied here yielded higher power rates when 2 latent classes were present, as opposed to 4. Thus, the BLRT can be said to yield the highest power among the methods studied here, while simultaneously maintaining the Type I error rate at approximately the nominal 0.05 level.
test and AIC. The BIC, CAIC, and aBIC all yielded much lower power than the other three methods. Furthermore, all of the methods studied here yielded higher power rates when 2 latent classes were present, as opposed to 4. Thus, the BLRT can be said to yield the highest power among the methods studied here, while simultaneously maintaining the Type I error rate at approximately the nominal 0.05 level.
3.4. Equivalence of Latent Class Prevalences: Type I Error Rate
ANOVA results for the Type I error rate for assessment of latent class prevalence equivalence across observed groups found that the only significant term was the interaction of method by group ratio![]() . Results in Table 5 reveal that for all of the methods, Type I error was larger when the group ratio was 3/1 as opposed to equal. In addition, except for BLRT and aBIC, all of the methods had rates above 0.06 in the unequal group size condition, while they all had rates of approximately 0.055 or lower for equal group sizes, with the exception of AIC.
. Results in Table 5 reveal that for all of the methods, Type I error was larger when the group ratio was 3/1 as opposed to equal. In addition, except for BLRT and aBIC, all of the methods had rates above 0.06 in the unequal group size condition, while they all had rates of approximately 0.055 or lower for equal group sizes, with the exception of AIC.
3.5. Equivalence of Latent Class Prevalences: Power
With respect to power for detecting a lack of latent class prevalence equivalence across groups, ANOVA identified two significant interactions: method by N by magnitude of noninvariance ![]() and method by group ratio by magnitude of noninvariance
and method by group ratio by magnitude of noninvariance![]() . An examination of Table 6 reveals that across simulated conditions, BLRT displayed the highest power rates except for the greatest magnitude of group separation and N of 200. While AIC generally had the second highest power rates across conditions, it must be noted that it also displayed inflated Type I error rates across all conditions simulated here, as discussed previously. Therefore, these results must be interpreted with caution. Among the other methods, the
. An examination of Table 6 reveals that across simulated conditions, BLRT displayed the highest power rates except for the greatest magnitude of group separation and N of 200. While AIC generally had the second highest power rates across conditions, it must be noted that it also displayed inflated Type I error rates across all conditions simulated here, as discussed previously. Therefore, these results must be interpreted with caution. Among the other methods, the ![]() test displayed the highest power rates, again except for magnitude of noninvariance = 0.3 and N of 500 or more, in which case all of the statistics had power of 1.00. Finally, for
test displayed the highest power rates, again except for magnitude of noninvariance = 0.3 and N of 500 or more, in which case all of the statistics had power of 1.00. Finally, for![]() , power never reached 0.8 for any of these techniques, except when the magnitude of difference was 0.3. For the lowest level of separation (0.05) the advantage of BLRT over the other methods was especially notable, particularly given that this method was also able to maintain the nominal Type I error rate of 0.05.
, power never reached 0.8 for any of these techniques, except when the magnitude of difference was 0.3. For the lowest level of separation (0.05) the advantage of BLRT over the other methods was especially notable, particularly given that this method was also able to maintain the nominal Type I error rate of 0.05.
Table 7 contains power rates by method, group ratio and difference. For lower values of difference, power rates of BLRT were greater than those of the other statistics. When magnitude = 0.3, power rates for all of the methods were just below 1.00. Thus, when the group prevalence rates differed by as much as 0.3, all of the statistics studied here were able to detect the noninvariance. Again, however, both ![]() and especially AIC had inflated Type I error rates for testing prevalence equality under many conditions, while BLRT did not.
and especially AIC had inflated Type I error rates for testing prevalence equality under many conditions, while BLRT did not.
![]()
Table 5. Type I error rate for testing equivalence of latent classes across groups, by method, class ratio, and group ratio.
![]()
Table 6. Power for testing prevalence equivalence of latent classes across groups, by testing method, magnitude of difference between groups (D), and sample size (N).
![]()
Table 7. Power for testing prevalence equivalence of latent classes across groups, by testing method, magnitude of difference between groups (D), and group size ratio.
3.6. Summary of Prevalence Equivalence Testing Results
The BLRT method of assessing the equivalence of latent class prevalences across the observed groups was able to maintain the nominal 0.05 Type I error rate across all conditions simulated here, while also yielding the highest power rates. Therefore, much as with measurement equivalence, it appears that BLRT is able to both maintain the Type I error rate and yield relatively high power when testing for the equivalence of latent class prevalence across observed groups.
3.7. Analysis of Youth Risk Behavior Survey Data
In this section of the manuscript an LCA invariance analysis for data from the Youth Risk Behavior Survey (YRBS) is conducted to compare latent class solutions across genders. The YRBS is a biennial survey administered by the United States Centers for Disease Control and Prevention (CDC) designed for high school students. It consists of self-reports of past and current thoughts, emotions, behaviors, and exposure to health relevant curriculum within schools, and provides a snapshot of the general health and risky behavior of America’s youth. The YRBS dataset is publicly available with individual identifying information, as well as school, state, and regional identifiers removed.
Of particular interest in this analysis is the assessment of gender differences in reckless behavior typologies among adolescents. Prior research has demonstrated that reckless physical behaviors increase in adolescence [28] . For example, as individuals move into their teen years the likelihood of their riding with an intoxicated driver increases [29] , while the likelihood of their regularly using their seatbelt in a car [30] , or wearing a helmet when riding a motorcycle decreases [31] . Furthermore, self care such as using sunscreen while outdoors [32] , or wearing a helmet when riding a bicycle [33] decline during this period as well. Finally, fighting has also been shown to increase in frequency and severity as individuals move from childhood to adolescence [34] . Coincident with this research demonstrating the increasing problem of reckless behavior in youth, there is also research to demonstrate that such risk taking may not be equally prevalent among males and females, and that in fact there may be some differences in the types of reckless behavior that are engaged in by the two genders [35] [36] .
Given this prior research, the goal of the current analysis was to investigate typologies of reckless behavior in the adolescent population using items from the YRBS, and to determine the extent to which these typologies were invariant for males and females. To this end, confirmatory LCA was used to ascertain whether the same number of latent classes was present for males and females, and if so whether there was measurement invariance for the items used to identify these latent classes, and if measurement invariance held, whether the prevalence of the latent classes was equivalent for the two genders. In short, the goal was to determine whether and to what extent reckless behavior typologies in the population are equivalent across males and females both in terms of the types of reported behaviors, and the relative frequency of the typologies in the population.
For this analysis, the items appearing in Table 8 (each coded as yes (1) or no (0)) were included in the inva- riance analysis. Each was selected because it measured a specific behavior that has been found in previous literature, cited above, to be associated with increased risk taking among adolescents. Of interest was whether the latent class solutions identified using these items were invariant for male and female respondents, first in terms of the number of latent classes found, second in terms of item response probabilities and if so, then third in terms of latent class prevalence. Based on the literature described above, it was anticipated that there would be distinct typologies of reckless behavior among adolescents, and that these patterns would differ by gender such that females would be relatively more risk averse than males.
![]()
Table 8. Latent class prevalence and response probabilities with 3 classes for the full sample.
A sample of 2000 subjects was drawn from the original YRBS data base, which contained 16,000 individuals. This sample of 2000 individuals was randomly drawn from among those who provided a valid response to each of the items appearing in Table 8 (a total of 13,743 respondents). In terms of gender, 1027 (51.9%) of the 2000 adolescents used in the LCA invariance analysis were male, as compared to 52.0% of those in the total sample. In order to cross-validate the results for this sample, we drew a second sample (without replacement) of 2000 individuals from the 11,743 remaining members of the YRBS data base who had responded to each of the items of interest, and conducted all of the analyses described below. While there were small differences in the percentages of respondents endorsing each item, the overall results (i.e. number of latent classes, noninvariance status) were the same for the second sample as for the first. This great similarity in the results for the two samples serves to support the results and conclusions described below.
Following the techniques for LCA invariance testing described in Collins and Lanza [5] , the first step was to identify the number of latent classes present in the sample as a whole. Four model solutions were fit to the YRBS data, for 2, 3, 4, and 5 latent classes. In order to determine the optimal number of latent classes, the fit indices described above, as well as model identification and interpretability of the solutions with regard to substantive meaning of the classes were considered. Based on the BLRT and the information indices, which appear in Table 9, particularly the AIC and aBIC, 3 latent classes appeared to fit the data best. Among the information indices, the aBIC in particular has been found to be most accurate in identifying the number of latent classes across a number of simulated conditions [14] [37] . In addition, research has found that among all currently available methods, the BLRT may be the most accurate approach for identifying the number of latent classes [6] . Therefore, given their generally greater accuracy, and the fact that they both (along with the AIC) identified the 3-class solution as optimal, this was the one selected here. In addition, a review of the nature of the latent classes, in terms of their item response profiles, suggested that the 3 latent class solution made substantive sense as well.
Table 8 includes the prevalence of each latent class, along with the proportion of individuals in the classes that endorsed each of the items used in the analysis, for the total sample. Based on these results, it appears that latent class 1 can be described as relatively high risk compared to the other two. Individuals in this group, which made up 25% of the total sample, were the least likely to use transportation safety devices such as seat belts in cars and helmets on bicycle/motorcycles, and were most likely to ride with a drinking driver and engage in
![]()
Table 9. Model fit indices for LCA models with the full sample and with each gender.
fighting in the last year. Latent class 2 was the most risk averse, being more likely to wear helmets on bicycles and motorcycles, more likely to wear a seat belt, and to use sunscreen, and the least likely to have ridden with a drinking driver or to have fought. Finally, latent class 3 displayed a pattern of behaviors that put them in between the highest and lowest risk groups.
After determining the number of latent classes for the sample as a whole, the next step was to establish that the number of latent classes and their general patterns of item responses were similar to those of the overall population. In other words, in order to test whether the item response probabilities for the two genders were invariant, we must first ensure that the number of latent classes in each was the same. LCA was applied to each gender individually, and as can be seen in Table 9, for both males and females the 3 class solution proved optimal, based on the AIC and aBIC. An examination of Table 10 shows that for each gender, latent class 1 reported relatively high rates of risky behavior, while latent class 2 reported the least risky behaviors and class 3 fell somewhere in between the two. Thus, it does appear that the basic constituencies of the latent classes were present for both males and females. Before we can talk about any gender differences in the prevalence of these behaviors for specific latent classes, we must first assess whether LCA invariance holds or not.
As described above, in order to determine whether measurement invariance holds, we fit two models. In the first model all item response probabilities were constrained to be equal across the genders, while in the second model they were all unconstrained. If the difference in model fit favored the unconstrained model (or was statistically significant in the case of the ![]() test) we would conclude that invariance did not hold. For both the constrained and unconstrained models, we fit the 3 class solution, given that it had already been established as optimal for both the full and gender specific samples. The fit statistics for the constrained and unconstrained models appear in Table 11, along with the
test) we would conclude that invariance did not hold. For both the constrained and unconstrained models, we fit the 3 class solution, given that it had already been established as optimal for both the full and gender specific samples. The fit statistics for the constrained and unconstrained models appear in Table 11, along with the ![]() test and BLRT. BLRT, the
test and BLRT. BLRT, the ![]() test, and AIC indicated that the
test, and AIC indicated that the
![]()
Table 10. Latent class prevalence and response probabilities with 3 classes by gender.
![]()
Table 11. Fit statistics and G2 difference test for the invariant and noninvariant models.
*p = 0.00000064.
noninvariant LCA model provided better fit to the data, while the BIC, CAIC and aBIC all suggested that the best fit was given by the constrained model. Based on the results of the simulation study described previously, it would appear that the BLRT, in particular, may provide more accurate results for measurement invariance than the other approaches, because it displays higher power while maintaining the nominal (0.05) Type I error rate. Thus we will work under the presumption that item response probabilities did differ between clusters across genders. An examination of Table 10 suggests that females in the highest risk group (latent class 1) were more likely to wear a safety belt, and less likely to fight or ride with a drinking driver than their male counterparts. Similarly, females in the lowest risk category (latent class 2), were less likely to engage in risky behaviors such as not wearing a bicycle helmet, not wearing sunscreen or fighting than were males in the low risk class. Indeed, the same pattern across genders was also seen in latent class 3, where females were less likely to engage in risky behaviors (i.e. not wearing a seat belt, fighting, not wearing a motorcycle helmet) than males, except for riding with a drinking driver, which they were actually more likely to do than were males in the corresponding latent class.
These results appear to support the a priori hypothesis that the nature of risk taking typologies differs between males and females. Male and female respondents did appear in the same basic latent classes based on their likelihood to engage in risky behaviors, including those who were relatively risk averse, those who were more likely to engage in reckless behavior, and a third group of individuals who were in the middle of the other two in terms of their likelihood to engage in reckless behavior. However, with respect to endorsement of specific reckless behaviors, females in each of these classes were more risk averse than their male counterparts, with the exception of latent class 3 and riding with a drinking driver. Thus, the hypothesis that there would be different typologies of individuals with respect to their propensity for engaging in reckless behaviors was upheld, as was the hypothesis that females would be less likely than males to engage in such behaviors regardless of typology. Given the lack of measurement invariance, it is not recommended that we test for the equality of latent class prevalences across groups [5] .
4. Discussion
The goal of this study was to compare several statistics in terms of their ability to correctly ascertain whether group invariance was present in the context of MGLCA. In addition, the use of MGLCA to conduct an invariance analysis with risk assessment items from the YRBS was also demonstrated. It is hoped that the results presented here will aid researchers from a variety of fields in successfully conducting invariance testing with LCA models. The outcomes described above suggest that BLRT is the optimal method, of those studied here, for assessing the invariance question. Whether considering measurement invariance or the equivalence of class prevalences, the BLRT most consistently maintained the Type I error rate of 0.05, while simultaneously yielding among the highest power values in the simulation study. This combination of Type I error control with relatively high power was particularly notable in the comparison of class prevalence estimates across groups, where virtually all of the other methods either kept the error rate at or below the nominal 0.05 level and had low power (i.e. CAIC, aBIC), or had higher power but were unable to control the Type I error rate (i.e.![]() , AIC). Considering the hypotheses built upon earlier work and stated above, it does appear that BLRT is the most accurate method for investigating LCA invariance. This result is in keeping with work by Nylund, Asparouhov and Muthén [6] showing that BLRT was also optimal for selecting the number of latent classes. In addition, the
, AIC). Considering the hypotheses built upon earlier work and stated above, it does appear that BLRT is the most accurate method for investigating LCA invariance. This result is in keeping with work by Nylund, Asparouhov and Muthén [6] showing that BLRT was also optimal for selecting the number of latent classes. In addition, the ![]() difference test did display some sensitivity to large sample size for assessing measurement invariance with 4 classes, but not in most other simulated conditions, thus partially matching earlier work showing its sensitivity to large N [20] . Additionally, as noted above, prior research in the LCA model selection literature found that AIC had a tendency to identify the presence of more latent classes in the sample than were actually present in the population [15] . This tendency to be overly liberal was evident for the AIC in comparing the equivalence of group prevalence estimates as well, where it too often indicated that the groups differed in this regard when they did not. Finally, consistent with the mixed results from the body of prior research with regard to information indices, no one of them was found to be clearly superior to the others. While the CAIC, BIC, and aBIC did not have the Type I error inflation of the AIC, neither did they have its power for rejecting the invariance null hypothesis when it was incorrect. For example, for determining whether the latent class specific item response probabilities differ across known groups (i.e. measurement invariance), the AIC and perhaps the
difference test did display some sensitivity to large sample size for assessing measurement invariance with 4 classes, but not in most other simulated conditions, thus partially matching earlier work showing its sensitivity to large N [20] . Additionally, as noted above, prior research in the LCA model selection literature found that AIC had a tendency to identify the presence of more latent classes in the sample than were actually present in the population [15] . This tendency to be overly liberal was evident for the AIC in comparing the equivalence of group prevalence estimates as well, where it too often indicated that the groups differed in this regard when they did not. Finally, consistent with the mixed results from the body of prior research with regard to information indices, no one of them was found to be clearly superior to the others. While the CAIC, BIC, and aBIC did not have the Type I error inflation of the AIC, neither did they have its power for rejecting the invariance null hypothesis when it was incorrect. For example, for determining whether the latent class specific item response probabilities differ across known groups (i.e. measurement invariance), the AIC and perhaps the ![]() performed better than did CAIC, BIC, or aBIC in terms of power and Type I error. Indeed, while having error rates at or near 0, these latter three methods also had very low power for measurement invariance when compared to the other techniques. Therefore, it is not clear that having such low error rates is truly a positive characteristic, given the concomitant low power rates, as it appears that these statistics are simply unlikely to reject the invariant model whether it is true or not. Finally, it was of interest that the aBIC did not perform better than the other information indices, although in some model selection studies it had been shown to be superior [13] [14] . Clearly, further investigation of this statistic in the context of confirmatory LCA is called for.
performed better than did CAIC, BIC, or aBIC in terms of power and Type I error. Indeed, while having error rates at or near 0, these latter three methods also had very low power for measurement invariance when compared to the other techniques. Therefore, it is not clear that having such low error rates is truly a positive characteristic, given the concomitant low power rates, as it appears that these statistics are simply unlikely to reject the invariant model whether it is true or not. Finally, it was of interest that the aBIC did not perform better than the other information indices, although in some model selection studies it had been shown to be superior [13] [14] . Clearly, further investigation of this statistic in the context of confirmatory LCA is called for.
In addition to providing insights into which statistics worked best under a variety of conditions, this study also revealed situations in which invariance testing in LCA might be somewhat more problematic. Specifically, when the observed groups differ in size by as much as a 3/1 ratio, several of the statistical approaches to assessing LCA invariance will be adversely affected, yielding lower power, particularly in the presence of more latent classes. On the other hand, the null hypothesis of equivalence of latent class prevalences will too frequently be rejected incorrectly in the unequal known group sample size case, with the exception of aBIC and BLRT. While the BLRT did have slightly lower power values in the 3/1 group ratio case, this difference was quite modest when compared to the other methods, typically decreasing by less than 0.05. In addition, study results show that when more latent classes are present in the population, the ability to accurately detect a lack of invariance may be compromised. Indeed, across most of the methods studied here and most of the simulated conditions, power for finding such differences declined from the 2 class condition. This decline was much less precipitous, however, for the BLRT when compared to the other methods.
4.1. Limitations and Directions for Future Research
By its very nature, simulation research presents some limitations in that the results are only generalizable to real world situations that mirror those simulated. While the conditions used here were selected in order to match real world examples in the literature, they could not be exhaustive. Therefore, future research in this area needs to continue in several directions. First of all, the observed variables simulated here were all dichotomous in nature. Thus, future studies should focus on the application of MGLCA to the case of polytomous data. In addition, the use of 5 indicators, while relatively common in practice, was not varied, so that subsequent work needs to expand the conditions for the number indicators so as to ascertain to what extent it may impact both types of invariance testing. The number of latent classes was also held constant for the two groups, which may not reflect all conditions encountered in actual practice. Therefore, future research should also consider cases when the number of classes in fact differs across observed groups. Likewise the number of groups was held constant at 2. While this is also very common in actual practice, it is nonetheless a limitation of this study in that we didn’t learn how well MGLCA can correctly determine invariance when the number of groups is larger. Finally, future studies should also examine a broader range of group size ratios. These results suggest strongly that the relative sizes of the groups matters, particularly in terms of testing the relative prevalence of latent classes. The two conditions simulated here, 1/1 and 3/1, were selected to represent two disparate and perhaps extreme cases. However, it would be very informative for practitioners wishing to use MGLCA to know at what point between the 1/1 and 3/1 ratios group size inequality becomes problematic.
4.2. Recommendations for Practice
The use of MGLCA for invariance testing offers great promise for researchers interested in questions regarding latent class model invariance. It is hoped that the current study provides researchers with information leading to optimal practice in LCA invariance testing. Based on these results, it would appear that, as is true with model selection [6] , the BLRT may be the optimal tool for assessing invariance in the context of LCA. It was able to both maintain the nominal Type I error rate across virtually all simulated conditions, and yielded power that was always as high as, or higher than the other methods. Furthermore, the BLRT worked relatively well for both types of invariance assessment, which was not the case for the other statistics studied here. For this reason, the BLRT appears to be an optimal choice. In addition, researchers must always consider the structure of their data when interpreting MGLCA results. The presence of relatively many latent classes, coupled with unequal observed group sizes will result in diminished power, even for BLRT. Thus, in such conditions, those engaged in invariance assessment must carefully consider the meaning of a non-significant test result. Nonetheless, the BLRT is clearly a promising method for assessing LCA invariance and as such should prove to be quite useful for researchers interested in using MGLCA to conduct this analysis.