Double-Penalized Quantile Regression in Partially Linear Models ()
1. Introduction
Since semiparametric regression models combine both parametric and nonparametric components, they are much more flexible than the linear regression model, and are easier interpretation of the effect of each variable than completely nonparametric regressions. Therefore, semiparametric regression models are very popular models in practical applications. In this paper, we consider a partially linear model
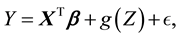 (1)
(1)
where 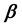 is a p-dimensional unknown parameter vector with its true value
is a p-dimensional unknown parameter vector with its true value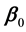 ,
, 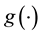 is a twice-differentiable unknown smooth function,
is a twice-differentiable unknown smooth function, 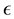 is independent of X and is a random error satisfying
is independent of X and is a random error satisfying . Since [1] first applied the partially linear model to study the relationship between weather and electricity sales, this model had received a considerable amount of research in the past several decades.
. Since [1] first applied the partially linear model to study the relationship between weather and electricity sales, this model had received a considerable amount of research in the past several decades.
In practice, many potential explanatory variables should be involved in this model, but the number of important ones is usually relatively small. Therefore, selection of important explanatory variables is often one of the most important goals in the real data analysis. In this paper, we are interested in automatic selection, and estimation for parametric components, and treat 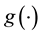 as a nuisance effect. There are many authors developed several approaches in the literature. For example, in the kernel smoothing framework, [2] first extended the penalized least squares criterion to partially linear models. [3] introduced a class of sieve estimators using a penalized least squares technique for semiparametric regression models. [4] studied variable selection for semiparametric regression models. [5] considered variable selection for partially linear models when the covariates were measured with additive errors. [6] combined the ideas of profiling and adaptive Elastic-Net [7] to select the important variables in X. In the framework of spline smoothing, [8] achieved sparsity in the linear part by using the SCAD- penalty [9] for partially linear models for high dimensional data, but the nonparametric function was estimated by the polynomial regression splines. [10] applied a shrinkage penalty on parametric components to obtain the significant variables and used the smoothing spline to estimate the nonparametric component.
as a nuisance effect. There are many authors developed several approaches in the literature. For example, in the kernel smoothing framework, [2] first extended the penalized least squares criterion to partially linear models. [3] introduced a class of sieve estimators using a penalized least squares technique for semiparametric regression models. [4] studied variable selection for semiparametric regression models. [5] considered variable selection for partially linear models when the covariates were measured with additive errors. [6] combined the ideas of profiling and adaptive Elastic-Net [7] to select the important variables in X. In the framework of spline smoothing, [8] achieved sparsity in the linear part by using the SCAD- penalty [9] for partially linear models for high dimensional data, but the nonparametric function was estimated by the polynomial regression splines. [10] applied a shrinkage penalty on parametric components to obtain the significant variables and used the smoothing spline to estimate the nonparametric component.
It is very important to note that many of those methods are closely related to the classical least squares method. It is well known that the least squares method is not robust and can produce large bias when there are outliers in the dataset. Therefore, the outliers can give rise to serious problems for the least squares based methods in variable selection. In this article, we propose the double-penalized quantile regression estimators. Based on the quantile regression loss function (check function), we apply a shrinkage penalty for parametric parts to yield the significant variables, and use the smoothing spline to estimate the nonparametric component. Simulation studies illustrate that the proposed method can achieve a consistent variable selection when there are outliers in the dataset or the error term follows a heavy-tailed distribution.
The rest of this paper is organized as follows. In Section 2, we first introduce the double-penalized quantile regression estimators in a partially linear regression model, and then propose an iterative algorithm to solve the proposed optimization problem. In Section 3, simulation studies are conducted to compare the finite-sample performance of the existing and proposed methods. In Section 4, we apply the proposed method to analyze a real data analysis. Finally, we conclude with a few remarks in Section 5.
2. Methodology and Main Results
2.1. Double-Penalized Quantile Regression Estimators
Suppose that  satisfy a following partially linear regression model,
satisfy a following partially linear regression model,
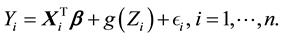 (2)
(2)
Without loss of generality, we assume that , and
, and 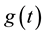 is in the Sobolev space V, where V is defined by
is in the Sobolev space V, where V is defined by
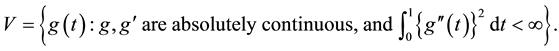
To simultaneously achieve the selection of important variables and the estimation of the nonparametric function , [10] proposed a double-penalized least squares (DPLS) estimators by minimizing
, [10] proposed a double-penalized least squares (DPLS) estimators by minimizing
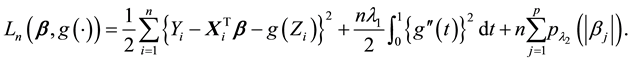
where  is nonnegative and nondecreasing functions in
is nonnegative and nondecreasing functions in . Under some regular conditions, [10] proved that the proposed estimators could be as efficient as the oracle estimator.
. Under some regular conditions, [10] proved that the proposed estimators could be as efficient as the oracle estimator.
To our knowledge, the ordinary least squares (OLS) estimator is not robust. If there are outliers in the dataset or the error follows a heavy-tailed distribution, it can product the large bias. In contrast to the least squares method, quantile regression introduced by [11] serves as a robust alternative since the asymptotic properties of quantile regression estimator do not depend on the variance of the error. In the following, we introduce a double-penalized quantile regression (DPQR) in partially linear models. For![]() , the DPQR estimators can be obtained by minimizing the following function,
, the DPQR estimators can be obtained by minimizing the following function,
![]() (3)
(3)
where![]() .
.
Let ![]() and the order statistics of a random sample
and the order statistics of a random sample ![]() be
be![]() and
and ![]() for
for![]() . According to [12] , we have
. According to [12] , we have
![]()
where K is an ![]() matrix given by
matrix given by![]() , Q is the
, Q is the ![]() matrix of second differences, with entries
matrix of second differences, with entries
![]()
![]()
R is a symmetric tridiagonal matrix of order ![]() with elements
with elements ![]()
![]()
![]()
Therefore, Equation (3) can be rewrote as
![]() (4)
(4)
2.2. Algorithm
To solve the optimization problem (4), we propose the following iterative algorithm. The estimation proce- dures are stated as follows:
Step 1 Given![]() , obtaining the estimator
, obtaining the estimator ![]() by minimizing the following objective function,
by minimizing the following objective function,
![]()
Step 2 Given![]() , obtaining
, obtaining ![]() by solving
by solving
![]()
Step 3 Repeat Step 1 and Step 2 until convergence.
Remark 1 In the above algorithm, we first obtain the initial estimators by minimizing the following objective function
![]() (5)
(5)
Let![]() . Given
. Given ![]() and
and![]() , we obtain
, we obtain ![]() by (5),
by (5),
![]()
where![]() , and
, and![]() . We plug
. We plug ![]() into (5), we have
into (5), we have
![]()
Finally, the estimator ![]() of nonparametric component is obtained as follows:
of nonparametric component is obtained as follows:
![]()
Remark 2 Since the check function ![]() is not smooth, we use the majorization-minimization (MM) algorithm introduced by [13] to optimize Step 1 and Step 2.
is not smooth, we use the majorization-minimization (MM) algorithm introduced by [13] to optimize Step 1 and Step 2.
Advocated in [14] , the check function ![]() can be approximated by its perturbation for some small
can be approximated by its perturbation for some small![]() ,
,
![]()
Furthermore, ![]() can be majorized at
can be majorized at ![]() by the following surrogate function given in [14] ,
by the following surrogate function given in [14] ,
![]()
The penalty functions can be approximated by the local quadratic approximation advocated in [15]
![]()
The minimization problem in Step 1 and Step 2 is a quadratic function after above these approximations, and can be solved in closed form. In our implementation, we set![]() .
.
3. Simulation Study
In this section, we conduct simulation studies to evaluate the finite-sample performance of the proposed estimators. We simulate 100 data sets from the following model (6) with sample sizes![]() .
.
![]() (6)
(6)
In this simulation, we choose![]() ,
, ![]() , Xi’s follows a 8-dimensional stan- dard normal distribution, and the error term follows the following two distributions: standard normal distribution
, Xi’s follows a 8-dimensional stan- dard normal distribution, and the error term follows the following two distributions: standard normal distribution![]() , and standard Cauchy distribution. We consider
, and standard Cauchy distribution. We consider![]() . Although the choice of penalized parameters l1 and l2 is very important, we take
. Although the choice of penalized parameters l1 and l2 is very important, we take ![]() in this paper. Meanwhile, we take the penal-
in this paper. Meanwhile, we take the penal-
ty function![]() , where
, where ![]() is a
is a ![]() -consistent estimator to
-consistent estimator to
![]() . For example, we can use least squares estimator.
. For example, we can use least squares estimator.
We compare our proposed estimators (DPQR) with the DPLS estimators and Oracle estimator based on the quantile regression. In order to measure the finite-sample performance, for the parameteric component, we calculate the non-causal selection rate (NSR) [9] , the positive selection rate (PSR) [16] as well as the median of the model error (MME) advocated by [9] , where the model error is defined as follows:
![]()
The simulation results are reported in Table 1 and Table 2. From Table 1, we can see that all these methods obtain the same PSR and NSR when the error term follows the standard normal distribution, but the DPLS estimator yields smaller the MME than the DPQR estimator and Oracle estimator. Whereas, when the error follows a Cauchy distribution, we find from Table 2 that the MME of our proposed method is smaller than the DPLS method. In variable selection, the PSR is around 1 for all three methods. However, what distinguishes DPQR from DPLS is NSR. Indeed, the NSR of the DPQR estimator is as close 1 as that of the oracle estimator, while the NSR of the DPLS estimator is about 30%. This illustrates that our proposed method leads to a consistent variable selection to errors with heavy tails.
4. Real Data Application
In this section, we illustrate our proposed double-penalized quantile regression method through application to
![]()
Table 1. Simulation results under normal error.
![]()
Table 2. Simulation results under cauchy error.
![]()
![]() (a) (b)
(a) (b)
Figure 1. (a) Histogram of y and (b) y against day.
![]()
Table 3. Estimated regression coefficients from the ragweed pollen level data.
the Ragweed Pollen Level data, which are collected in Kalamazoo, Michigan during the 1993 ragweed season. This dataset consists of 87 observations, and contains the following four variables: ragweed (the daily ragweed pollen level (grains/m3)), rain x1 (indicator of significant rain of the following day: 1 = at least 3 hours of steady or brief but intense rain, 0 = otherwise), temperature x2 (temperature of following day (degrees Fahrenheit)), wind speed x3 (wind speed forecast for following day (knots)), and day (day number in the current ragweed pollen season). The ragweed is the response variable, and the rest are the explanatory variables.
The goal is to understand the effect of the explanatory variables on ragweed, and to obtain accurate models to predict the ragweed. According to [17] , we take![]() . Histogram of y in Figure 1(a) indicates that the response is rather skewed. Therefore, there are outliers in the response or the error follows a heavy-tailed distribution. In addition, we plot y against day in Figure 1(b). From Figure 1(b), we can find that there is a strong nonlinear relationship between y and the day number. As a consequence, a semiparametric regression model with a nonparametric baseline g (day) is very reasonable. In this paper, we add some quadratic and inte- raction terms, and consider a more complex semiparametric regression model.
. Histogram of y in Figure 1(a) indicates that the response is rather skewed. Therefore, there are outliers in the response or the error follows a heavy-tailed distribution. In addition, we plot y against day in Figure 1(b). From Figure 1(b), we can find that there is a strong nonlinear relationship between y and the day number. As a consequence, a semiparametric regression model with a nonparametric baseline g (day) is very reasonable. In this paper, we add some quadratic and inte- raction terms, and consider a more complex semiparametric regression model.
In the following, we apply the DPLS method and DPQR method to fit the semiparametric regression model. For the DPQR method, we take![]() . The results are summarized in Table 3. From Table 3, we find that there also exists a nonlinear relationship between y and temperature and between y and wind speed by the DPQR method.
. The results are summarized in Table 3. From Table 3, we find that there also exists a nonlinear relationship between y and temperature and between y and wind speed by the DPQR method.
5. Discussion
In this paper, we introduced a double-penalized quantile regression method in partially linear models. The merits of our proposed methodology were illustrated via simulation studies and a real data analysis. According to numerical simulations, our proposed method could achieve a consistent variable selection when there were outliers in the dataset or the error followed a heavy-tailed distribution.
Acknowledgements
Jiang’s research is partially supported by the National Natural Science Foundation of China (No.11301221).