1. Introduction
The composite fermion theory introduces a quasi-particle named composite fermion which is an electron bound by even number 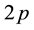 of flux quanta. The theory explains the fractional quantum Hall effect (FQHE) to be the integer quantum Hall effect (IQHE) of the composite fermions with an integer filling factor n. Then the filling factor of electrons becomes
of flux quanta. The theory explains the fractional quantum Hall effect (FQHE) to be the integer quantum Hall effect (IQHE) of the composite fermions with an integer filling factor n. Then the filling factor of electrons becomes 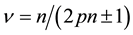 [1] -[12] . The case of n = 1 and
[1] -[12] . The case of n = 1 and 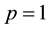 yields
yields  and
and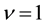 . The other cases give the electron filling-factors
. The other cases give the electron filling-factors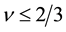 . Thus the original composite fermion theory cannot explain the fractional quantum Hall states with
. Thus the original composite fermion theory cannot explain the fractional quantum Hall states with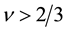 . In order to remove this difficulty, an extended theory has been considered as follows:
. In order to remove this difficulty, an extended theory has been considered as follows:
1) At the filling factor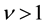 , the IQHE of composite fermions are combined with the IQHE of electrons. Even number of the flux quanta attach to some electrons and the other electrons are not bound by flux quanta. The former electrons are affected by the effective magnetic field and the latter by the applied magnetic field.
, the IQHE of composite fermions are combined with the IQHE of electrons. Even number of the flux quanta attach to some electrons and the other electrons are not bound by flux quanta. The former electrons are affected by the effective magnetic field and the latter by the applied magnetic field.
2) In the region of ![]() even number of flux quanta attach to a hole. Therein the electrons are not bound by flux quanta.
even number of flux quanta attach to a hole. Therein the electrons are not bound by flux quanta.
3) The effective magnetic field is anti-parallel to the applied magnetic field at![]() . So the polarization of electron at
. So the polarization of electron at ![]() is opposite to that at
is opposite to that at![]() .
.
Thus the direction of the effective field, the kind of particle (hole or electron) and the number of attached flux quanta are assumed to change with variation of the filling factor. This changing is very artificial. There is another investigation considered by Tao and Thouless [13] [14] . They investigated the FQH states where the Landau orbitals in the lowest level are partially filled with electrons.
We have improved the Tao-Thouless theory on the basis of the fundamental method. There are many configurations of electrons in the Landau orbitals. The sum of the Landau energy, classical Coulomb energy and Zeeman energy takes the minimum value at only one configuration of electrons for any fractional filling factor. In the configuration the nearest electron pairs can transfer to all the empty orbitals for the specific filling factors.
We consider the 2D electron system under a low temperature and a strong magnetic field throughout the present article. When the direction of the magnetic field is upward, the Zeeman energy of down-spin is lower than that of up-spin for electrons. So, in the region ![]() all the Landau orbitals in the lowest level are occupied by the electrons with down-spin. On the other hand the Landau orbitals are partially occupied by up-spins. (Note: In the previous papers [15] -[19] we have already examined the case of a weak magnetic field. In the case both down- and up-spin-electrons partially occupy the lowest Landau orbitals. This special case appears in a weak magnetic field by adjusting the gate voltage. In this paper we investigate only the case of a strong magnetic field.) The up-spin electron pair placed in the nearest orbitals can transfer to all the empty orbitals of up-spin at
all the Landau orbitals in the lowest level are occupied by the electrons with down-spin. On the other hand the Landau orbitals are partially occupied by up-spins. (Note: In the previous papers [15] -[19] we have already examined the case of a weak magnetic field. In the case both down- and up-spin-electrons partially occupy the lowest Landau orbitals. This special case appears in a weak magnetic field by adjusting the gate voltage. In this paper we investigate only the case of a strong magnetic field.) The up-spin electron pair placed in the nearest orbitals can transfer to all the empty orbitals of up-spin at![]() ,
, ![]() and so on. When the filling factor
and so on. When the filling factor ![]() deviates from
deviates from![]() , the number of allowed transitions decrease abruptly in comparison with that at
, the number of allowed transitions decrease abruptly in comparison with that at![]() . This mechanism creates the energy gaps at
. This mechanism creates the energy gaps at![]() ,
, ![]() ,
, ![]() ,
, ![]() and so on. These energy gaps can explain the fractional quantum Hall effect in the region
and so on. These energy gaps can explain the fractional quantum Hall effect in the region ![]() as clarified in the following sections. (We have already succeeded to obtain the energy gaps for the specific filling factors in the regions
as clarified in the following sections. (We have already succeeded to obtain the energy gaps for the specific filling factors in the regions ![]() and
and ![]() in the previous articles [20] -[30] .)
in the previous articles [20] -[30] .)
2. The Fundamental Properties of a Quasi-2D Electron System
Figure 1 shows a quantum Hall device where the electric current flows along the x-axis and the Hall voltage appears along the y-axis. Therein the magnetic field is applied in the z-direction.
The narrow potential ![]() along the z-direction is expressed in Figure 2. Also Figure 3 shows the potential
along the z-direction is expressed in Figure 2. Also Figure 3 shows the potential ![]() of the y-direction. Therein the voltage
of the y-direction. Therein the voltage ![]() is not zero because the confinement of Hall resistance is realized under a nonzero value of
is not zero because the confinement of Hall resistance is realized under a nonzero value of![]() . The value of the Hall voltage is extremely larger than the potential voltage in the FQHE. So we cannot employ the x - y symmetry. Also we should take the potential
. The value of the Hall voltage is extremely larger than the potential voltage in the FQHE. So we cannot employ the x - y symmetry. Also we should take the potential ![]() into consideration.
into consideration.
The vector potential, ![]() , has the components,
, has the components,
![]() (1)
(1)
where ![]() is the strength of the magnetic field. (Here we cannot use the symmetric vector potential because of the potential
is the strength of the magnetic field. (Here we cannot use the symmetric vector potential because of the potential![]() .) We express the single electron Hamiltonian,
.) We express the single electron Hamiltonian, ![]() , in the absence of the Coulomb interaction between electrons as,
, in the absence of the Coulomb interaction between electrons as,
![]() (2)
(2)
where ![]() and
and ![]() indicate the potentials confining electrons to an ultra-thin conducting layer. Therein
indicate the potentials confining electrons to an ultra-thin conducting layer. Therein ![]() is an effective mass of electron and
is an effective mass of electron and ![]() is the electron momentum. The last term of Equation (2) indicates the Zeeman energy where
is the electron momentum. The last term of Equation (2) indicates the Zeeman energy where ![]() is the effective g-factor,
is the effective g-factor, ![]() is the Bohr magneton
is the Bohr magneton ![]() and
and ![]() is the z-component of electron spin operator as,
is the z-component of electron spin operator as,
![]() (3)
(3)
The potential along the x-axis doesn’t exist in the Hamiltonian![]() . (The impurity effect is ignored.) Therefore the eigen-states along the direction
. (The impurity effect is ignored.) Therefore the eigen-states along the direction ![]() is the plain wave. Then the Landau wave function of the single- electron is given by
is the plain wave. Then the Landau wave function of the single- electron is given by
![]() (4a)
(4a)
![]() (4b)
(4b)
![]() (4c)
(4c)
![]() (4d)
(4d)
where ![]() is the wave function of the ground state along the z-direction,
is the wave function of the ground state along the z-direction, ![]() is the Hermite polynomial of
is the Hermite polynomial of ![]() -th degree,
-th degree, ![]() is the normalization constant and
is the normalization constant and ![]() is the length of a quasi-2D electron system as shown in Figure 1. The integer
is the length of a quasi-2D electron system as shown in Figure 1. The integer ![]() is called Landau level number hereafter. The momentum
is called Landau level number hereafter. The momentum ![]() of the x-direction satisfies the periodic boundary condition, and is related to the value
of the x-direction satisfies the periodic boundary condition, and is related to the value ![]() as in Equation (4d). The eigen-energy is given by
as in Equation (4d). The eigen-energy is given by
![]() (5)
(5)
where ![]() is the ground state energy along the z-direction and
is the ground state energy along the z-direction and ![]() is the potential energy in the y-direction. The energy difference between two Zeeman levels is equal to
is the potential energy in the y-direction. The energy difference between two Zeeman levels is equal to![]() . Here the effective g-factor for GaAs is about 0.22 times the g-factor of electron in vacuum, namely,
. Here the effective g-factor for GaAs is about 0.22 times the g-factor of electron in vacuum, namely,![]() . The effective mass
. The effective mass ![]() for GaAs is 0.067 times the electron mass m in vacuum. Therefore the energy difference between
for GaAs is 0.067 times the electron mass m in vacuum. Therefore the energy difference between ![]() and
and ![]() Landau levels is about 67 times the Zeeman split energy for GaAs.
Landau levels is about 67 times the Zeeman split energy for GaAs.
Many investigations of the FQHE have used the symmetric property between the ![]() and
and ![]() directions. However all the actual experiments have carried out in a nonzero voltage
directions. However all the actual experiments have carried out in a nonzero voltage![]() . Accordingly the potential
. Accordingly the potential ![]() cannot be ignored.
cannot be ignored.
If we take the other types of the vector potential as
![]() (6)
(6)
the eigen-function in the y-direction is not a plain wave because of the y-dependence of![]() . Consequently the actual quantum Hall system has no
. Consequently the actual quantum Hall system has no ![]() symmetry.
symmetry.
Our treatment takes the potential ![]() into consideration which is the appropriate treatment in an actual system. In a many-electron system the total Hamiltonian is given by the following equation as
into consideration which is the appropriate treatment in an actual system. In a many-electron system the total Hamiltonian is given by the following equation as
![]() (7)
(7)
where ![]() is the total number of electrons,
is the total number of electrons, ![]() is the permittivity and
is the permittivity and ![]() is the single particle Hamiltonian of the i-th electron without the Coulomb interaction as,
is the single particle Hamiltonian of the i-th electron without the Coulomb interaction as,
![]() (8)
(8)
where ![]() indicates the z-component of the spin for the i-th electron.
indicates the z-component of the spin for the i-th electron.
The many-electron state is characterized by a set of Landau level numbers![]() , a set of momenta
, a set of momenta ![]() and spins
and spins![]() . The complete set is composed of the Slater determinant as
. The complete set is composed of the Slater determinant as
![]() (9)
(9)
These states are the eigen-state of![]() . The expectation value of the total Hamiltonian is expressed by
. The expectation value of the total Hamiltonian is expressed by
![]() which is given as:
which is given as:
![]() (10)
(10)
where ![]() is the expectation value of the Coulomb interaction as follows:
is the expectation value of the Coulomb interaction as follows:
![]() (11)
(11)
Hereafter we call ![]() “classical Coulomb energy”. Using the expectation value W, we can divide the total Hamiltonian
“classical Coulomb energy”. Using the expectation value W, we can divide the total Hamiltonian ![]() into the two parts
into the two parts ![]() and
and ![]() as follows:
as follows:
![]() (12a)
(12a)
![]() (12b)
(12b)
where ![]() is composed of the off-diagonal elements only. Accordingly the total Hamiltonian
is composed of the off-diagonal elements only. Accordingly the total Hamiltonian ![]() of the quasi-2D electron system is a sum of
of the quasi-2D electron system is a sum of ![]() and
and ![]() as
as
![]() (13)
(13)
Because the Coulomb interaction depends only upon the relative coordinate of electrons, the total momentum along the x-direction conserves in the quasi-2D electron system. That is to say the sum of the initial momenta ![]() and
and ![]() is equal to that of the final momenta
is equal to that of the final momenta ![]() and
and![]() :
:
![]() (14)
(14)
We study the configuration of electrons in the Landau orbitals. The most uniform configuration of electrons is uniquely determined for any filling factor except at the both boundaries. The boundary effects can be neglected in a macroscopic system.
As seen in Equation (8), the ![]() state has an energy lower than the
state has an energy lower than the ![]() state for
state for![]() . Therefore at
. Therefore at ![]() all the Landau orbitals with
all the Landau orbitals with ![]() are occupied by electrons with down-spin and the orbitals are partially occupied by electrons with up-spin in a strong magnetic field and a low temperature. We introduce the total number
are occupied by electrons with down-spin and the orbitals are partially occupied by electrons with up-spin in a strong magnetic field and a low temperature. We introduce the total number ![]() of the
of the ![]() orbitals and also express the number of electrons with down-spin and up-spin by
orbitals and also express the number of electrons with down-spin and up-spin by ![]() and
and ![]() respectively. Then we get the following relations in
respectively. Then we get the following relations in ![]() as
as
![]() (15a)
(15a)
![]() (15b)
(15b)
![]() (15c)
(15c)
![]() (15d)
(15d)
The most uniform configurations will be examined for the case of ![]() in Section 3 and for
in Section 3 and for ![]() in Section 4.
in Section 4.
3. Electron Configurations and Energy Gaps for ![]()
As an example we examine the FQH state with![]() . Equation (15d) becomes
. Equation (15d) becomes
![]()
This relation gives
![]() (16)
(16)
Then the most uniform configuration of up-spin electrons is the repeat of (filled, empty, filled) for![]() . Figure 4 shows the electron configuration in a 3D view where the
. Figure 4 shows the electron configuration in a 3D view where the![]() ,
, ![]() ,
, ![]() axes are drawn in the upper-left of the figure. Therein the tilted lines with the x-direction express the Landau orbitals of the lowest level schematically. All the orbitals are filled with down-spin electrons for a strong magnetic field because of the Zeeman energy. The up-spin electrons occupy the red-coloured orbitals. The empty orbitals for up-spin are drawn by dashed blue lines in Figure 4. This electron configuration of up-spin has the minimum value for the classical Coulomb energy.
axes are drawn in the upper-left of the figure. Therein the tilted lines with the x-direction express the Landau orbitals of the lowest level schematically. All the orbitals are filled with down-spin electrons for a strong magnetic field because of the Zeeman energy. The up-spin electrons occupy the red-coloured orbitals. The empty orbitals for up-spin are drawn by dashed blue lines in Figure 4. This electron configuration of up-spin has the minimum value for the classical Coulomb energy.
We examine the quantum transitions via the Coulomb interaction![]() . All the Coulomb transitions satisfy the momentum conservation along the x-axis. Figure 4 shows the quantum transitions from the electron pair AB with up-spin. The momenta at A and B are expressed by
. All the Coulomb transitions satisfy the momentum conservation along the x-axis. Figure 4 shows the quantum transitions from the electron pair AB with up-spin. The momenta at A and B are expressed by ![]() and
and ![]() respectively. The momenta
respectively. The momenta ![]() and
and ![]() change to
change to ![]() and
and ![]() after the transition. The momentum conservation gives the following relations as
after the transition. The momentum conservation gives the following relations as
![]() (17a)
(17a)
![]() (17b)
(17b)
where ![]() is the momentum transfer. All the allowed transitions are illustrated by the blue allow-pairs in Figure 4. Accordingly the transfer momentum takes the following value:
is the momentum transfer. All the allowed transitions are illustrated by the blue allow-pairs in Figure 4. Accordingly the transfer momentum takes the following value:
![]() (18)
(18)
We introduce the following summation![]() .
.
![]() (19a)
(19a)
![]() (19b)
(19b)
![]() (19c)
(19c)
Therein the summation is carried out for all the values ![]() except
except ![]() and
and![]() . The elimination comes from disappearance of the diagonal matrix element of
. The elimination comes from disappearance of the diagonal matrix element of![]() . The summation
. The summation ![]() is positive, because the denominator in Equation (19a) is negative.
is positive, because the denominator in Equation (19a) is negative.
As shown in Figure 4, the transfer-momenta from AB (up-spin electron-pair) satisfies Equation (18). Then the number of the transfer-momenta is 1/3 of the total orbitals. Accordingly the perturbation energy ![]() of the pair AB is expressed by using
of the pair AB is expressed by using ![]() as follows;
as follows;
![]() (20)
(20)
because the momentum-interval, ![]() , is extremely small in a macroscopic size of a quantum Hall device. The total number of the nearest electron pairs with up-spin is 1/2 of
, is extremely small in a macroscopic size of a quantum Hall device. The total number of the nearest electron pairs with up-spin is 1/2 of![]() . Therefore we obtain the nearest pair energy per up-spin-electron
. Therefore we obtain the nearest pair energy per up-spin-electron ![]() as
as
![]() (21)
(21)
When the filling factor deviates from![]() , the electron configuration at
, the electron configuration at ![]() changes from the regular repeating of (filled, empty, filled). Accordingly the number of the Coulomb transitions decreases abruptly because the changing disturbs the Coulomb transitions. As an example, the
changes from the regular repeating of (filled, empty, filled). Accordingly the number of the Coulomb transitions decreases abruptly because the changing disturbs the Coulomb transitions. As an example, the ![]() state is illustrated in Figure 5 where the nearest orbitals with up-spin are indicated by red and brown colours.
state is illustrated in Figure 5 where the nearest orbitals with up-spin are indicated by red and brown colours.
There are 9 nearest electron pairs, namely, AB, CD, EF, GH, IJ, KL, MN, OP and PQ in every unit sequence. The pair CD can transfer to two orbital pairs per unit length as shown by black arrow pairs. Accordingly the perturbation energy ![]() is equal to
is equal to
![]() (22)
(22)
The pair AB can transfer to all the empty orbitals of up-spin and then the number of allowed transitions is eight per unit length. Therefore the perturbation energy ![]() is
is
![]() (23)
(23)
The other pairs have the perturbation energies as
![]() (24)
(24)
The sum of the nearest electron pairs with up-spin is
![]() (25)
(25)
The number of electrons with up-spin is seventeen in a unit sequence. Therefore the nearest pair energy per up-spin electron is
![]() (26)
(26)
When the filling factor ![]() is
is ![]() (s is a positive integer), the sum of the nearest-pair-energies inside the unit sequence is
(s is a positive integer), the sum of the nearest-pair-energies inside the unit sequence is
![]() (27)
(27)
The filling factor ![]() is larger than 5/3. The number of up-spin-electrons inside a unit length is equal to
is larger than 5/3. The number of up-spin-electrons inside a unit length is equal to ![]() and therefore the pair energy per up-spin-electron is given by
and therefore the pair energy per up-spin-electron is given by
![]() (28)
(28)
When s becomes infinitely large, ![]() approaches
approaches
![]() (29)
(29)
Next we consider the filing factor 38/23 which is smaller than 5/3. The most uniform configuration is illustrated in Figure 6.
In this case, the sum of the nearest-pair-energies inside the unit sequence is
![]() (30)
(30)
At![]() , the sum of the nearest-pair-energies inside the unit sequence is
, the sum of the nearest-pair-energies inside the unit sequence is
![]() (31)
(31)
Accordingly
![]() (32)
(32)
![]() (33)
(33)
Thus the energy gap appears between the energy value at ![]() and the limiting value from the left and right sides:
and the limiting value from the left and right sides:
![]() (34)
(34)
At the filling factor![]() , the energy gaps are listed in the fourth column of Table 1.
, the energy gaps are listed in the fourth column of Table 1.
We consider the other cases. Figure 7 shows the most uniform configuration of electrons at the filling factor![]() . The x-, y-, z-directions are indicated at the upper-left of Figure 7.
. The x-, y-, z-directions are indicated at the upper-left of Figure 7.
The unit configuration is composed of five Landau orbitals and three electrons with up-spin. The number of the allowed transitions is two per unit length. Accordingly the perturbation energy ![]() of the pair AB is expressed by
of the pair AB is expressed by ![]() as
as
![]() (35)
(35)
The total number of the nearest electron pairs with up-spin is 1/3 times![]() . Therefore the nearest pair energy per up-spin-electron is
. Therefore the nearest pair energy per up-spin-electron is
![]() (36)
(36)
When the filling factor deviates from![]() , the number of the Coulomb transitions decreases abruptly because the electron configuration at
, the number of the Coulomb transitions decreases abruptly because the electron configuration at ![]() disturbs the Coulomb transitions. As an example, the
disturbs the Coulomb transitions. As an example, the ![]() state is illustrated in Figure 8.
state is illustrated in Figure 8.
There are five up-spin-electron pairs placed in the nearest orbitals inside a unit length as in Figure 8. The number of allowed transitions is eleven for the pair AB, nine for EF and seven for CD in a unit length. Therefore the perturbation energies are obtained as follows:
![]() (37)
(37)
The sum of these pair energies is
![]() (38)
(38)
The number of electrons with up-spin is sixteen in a unit length and then the nearest pair energy per up-spin- electron is
![]() (39)
(39)
We examine more general cases of![]() . In the filling factor, the sum of the nearest-pair- energies inside a unit length is
. In the filling factor, the sum of the nearest-pair- energies inside a unit length is
![]() (40)
(40)
Accordingly
![]() (41)
(41)
![]() (42)
(42)
Next we study the FQH state with![]() . The most uniform configuration is illustrated in Figure 9.
. The most uniform configuration is illustrated in Figure 9.
The perturbation energy of the pair AB is
![]() (43)
(43)
The number of the nearest electron pairs with up-spin is 1/4 of![]() . Therefore the nearest pair energy per up-spin-electron is
. Therefore the nearest pair energy per up-spin-electron is
![]() (44)
(44)
At ![]() the perturbation energy
the perturbation energy ![]() for the nearest pair AB is obtained as
for the nearest pair AB is obtained as
![]() (45)
(45)
The total number of the nearest electron pairs with up-spin is ![]() times
times![]() . Therefore the nearest pair energy per up-spin-electron is
. Therefore the nearest pair energy per up-spin-electron is
![]() (46)
(46)
The energies are listed in the second column of Table 2. Next we calculate the number of the allowed transitions in the neighbourhood of![]() . Then the energy gaps are shown in the fourth column of Table 2.
. Then the energy gaps are shown in the fourth column of Table 2.
Thus the present theory yields the energy gaps at the specific filling factors as in Table 1 and Table 2.
4. Electron Configurations and Energy Gaps for ![]()
We examine the FQH states with ![]() in this section. Four examples are shown in Figures 10-13 where the filling factors are
in this section. Four examples are shown in Figures 10-13 where the filling factors are![]() , 6/5, 7/5 and 10/7, respectively. The electron configurations are illustrated in a 3D view where the down-spin electrons occupy all the Landau orbitals with the lowest level.
, 6/5, 7/5 and 10/7, respectively. The electron configurations are illustrated in a 3D view where the down-spin electrons occupy all the Landau orbitals with the lowest level.
The most uniform electron configuration with up-spin is the repeat of the sequence (empty, filled, empty) at ![]() as in Figure 10. The empty orbitals for up-spin are shown by red dashed lines and the filled orbitals
as in Figure 10. The empty orbitals for up-spin are shown by red dashed lines and the filled orbitals
with up-spin by blue lines. The blue arrows express the quantum transitions to the empty pairs AB. The symbol ![]() means the perturbation energy via all the quantum transitions shown by blue arrow pairs. The nearest vacant-orbital-pair (nearest hole pair) AB is specified by the momenta
means the perturbation energy via all the quantum transitions shown by blue arrow pairs. The nearest vacant-orbital-pair (nearest hole pair) AB is specified by the momenta![]() . The electron pair A'B' is also specified by the momenta
. The electron pair A'B' is also specified by the momenta![]() . The electron pair A'B' transfers to the vacant orbitals at A and B. Therein the total momentum of the pair conserves in the Coulomb transition as
. The electron pair A'B' transfers to the vacant orbitals at A and B. Therein the total momentum of the pair conserves in the Coulomb transition as
![]() (47)
(47)
where the momentum transfer ![]() takes the following values as
takes the following values as
![]() (48)
(48)
at![]() . Then the second order perturbation energy of the hole pair AB is given by
. Then the second order perturbation energy of the hole pair AB is given by
![]() (49)
(49)
In order to evaluate the energy ![]() we introduce the summation
we introduce the summation ![]() as
as
![]() (50)
(50)
where the momentum transfer ![]() takes all the values
takes all the values ![]() except
except ![]() and
and![]() . The transferred state for
. The transferred state for ![]() or
or ![]() is eliminated in the summation (50) because the diagonal element of
is eliminated in the summation (50) because the diagonal element of ![]() is absent. The denominator in Equation (50) is negative and so
is absent. The denominator in Equation (50) is negative and so ![]() is positive. (The value of
is positive. (The value of ![]() is nearly equal to
is nearly equal to ![]() for the same magnetic field strength.) The interval of momentum transfer is very small for a macroscopic size of a device and therefore the perturbation energy,
for the same magnetic field strength.) The interval of momentum transfer is very small for a macroscopic size of a device and therefore the perturbation energy, ![]() , can be expressed by
, can be expressed by ![]() as
as
![]() (51)
(51)
The electron configurations at![]() , 7/5 and 10/7 are illustrated in Figures 11-13, respectively.
, 7/5 and 10/7 are illustrated in Figures 11-13, respectively.
The perturbation energies, ![]() , are also obtained by making use of
, are also obtained by making use of ![]() as follows:
as follows:
![]() (52a)
(52a)
![]() (52b)
(52b)
![]() (52c)
(52c)
In the unit length there are 1, 2, or 3 electrons for the filling factor![]() , 7/5, or 10/7, respectively. Therefore the energy per electron becomes
, 7/5, or 10/7, respectively. Therefore the energy per electron becomes![]() ,
, ![]() and
and![]() . We express the perturbation energy per electron by the symbol
. We express the perturbation energy per electron by the symbol ![]() at
at ![]() which is listed in the second column of Table 3.
which is listed in the second column of Table 3.
The limiting values from both sides are calculated and written in the third column of Table 3. Subtractions of the limiting value from ![]() give the energy gaps which are listed in the fourth column of Table 3. Tables 1-3 show the energy gaps at many filling factors. Thus the present theory can explain the confinement of the Hall resistance in the region of
give the energy gaps which are listed in the fourth column of Table 3. Tables 1-3 show the energy gaps at many filling factors. Thus the present theory can explain the confinement of the Hall resistance in the region of![]() .
.
5. Filling Factors with Even Integer for the Denominator
We examine the ![]() state as an example with even integer for the denominator of the filling factor. Figure 14 shows the most uniform configuration at
state as an example with even integer for the denominator of the filling factor. Figure 14 shows the most uniform configuration at![]() .
.
There are many electron pairs in Figure 14. The pair AB is an example of the nearest electron pair. The
quantum transition via the Coulomb interaction conserves the total momentum. Accordingly the electron B should transfer to one orbital to the right when the electron A transfers to one orbital to the left. However the transformation to the right-direction is forbidden because the Landau orbital is already occupied by up-spin electron as shown by the blue arrows on Figure 14. When the electron A transfers to the fifth orbital to the left, the electron B cannot transfer to the fifth orbital to the right because of the Pauli exclusion principle. Thus all the transitions from the nearest electron pairs are forbidden via the Coulomb interaction. Therefore the electron pair AB has no binding energy. Also all the quantum transition from the electron pair BC are forbidden. Accordingly all the nearest electron pairs have no binding energy.
Similarly all the nearest electron pairs have no binding energy at the filling factor![]() .
.
![]() (53)
(53)
The energies are listed in the second column of Table 4.
We examine the energies of the nearest electron pairs in the neighbourhood of![]() . As an example for the neighbourhood of
. As an example for the neighbourhood of![]() , we have calculated the number of allowed transitions by using a computer, then we obtain
, we have calculated the number of allowed transitions by using a computer, then we obtain
![]() (54a)
(54a)
![]()
Table 4. Comparison of nearest electron pair energies at ![]() and in its neighbourhood.
and in its neighbourhood.
![]() (54b)
(54b)
![]() (54c)
(54c)
![]() (54d)
(54d)
The limiting value of the pair energy for ![]() is obtained as follows:
is obtained as follows:
![]() (55)
(55)
Next we examine the case of![]() .
.
![]() (56a)
(56a)
![]() (56b)
(56b)
![]() (56c)
(56c)
![]() (56d)
(56d)
For the limiting of ![]() the nearest pair energy approaches
the nearest pair energy approaches
![]() (57)
(57)
On the other hand the nearest pair energy at ![]() is zero as obtained in Equation (53). Therefore the pair energy at
is zero as obtained in Equation (53). Therefore the pair energy at ![]() is higher than the energy in the neighbourhood of
is higher than the energy in the neighbourhood of![]() . Then the peak values are listed in the fourth column of Table 4.
. Then the peak values are listed in the fourth column of Table 4.
Similarly we calculate the quantum transition energy to the nearest empty orbitals at the filling factor![]() . The values are listed in Table 5.
. The values are listed in Table 5.
Thus the FQH state is not stable at ![]() and
and![]() , because the energy is higher than that of the neighbourhood. That is to say, the Hall resistance confinement doesn’t appear at
, because the energy is higher than that of the neighbourhood. That is to say, the Hall resistance confinement doesn’t appear at ![]() and
and![]() . This theoretical result is in agreement with the experimental data.
. This theoretical result is in agreement with the experimental data.
6. Discussions
We have investigated the FQH states on the bases of the electromagnetic theory and the quantum theory without
![]()
Table 5. Comparison of nearest electron pair energies at ![]() and in its neighbourhood.
and in its neighbourhood.
any quasi-particle. There are the other famous theories explaining the FQHE which are the Haldane-Halperin hierarchy theory and the composite fermion theory. Recently J.K. Jain has examined the distinct difference between them [31] . Also he summarized the composite fermion theory. The composite fermion theory deals with FQH states by dividing into several types as follows: We study the composite fermion theory for the electron filling-factors with the denominator smaller than 6 namely![]() , 2/3, 4/3, 5/3, 1/5, 2/5, 3/5, 4/5, 6/5, 7/5, 8/5 and 9/5. These FQH states have the following structures as mentioned in the reference [31] .
, 2/3, 4/3, 5/3, 1/5, 2/5, 3/5, 4/5, 6/5, 7/5, 8/5 and 9/5. These FQH states have the following structures as mentioned in the reference [31] .
(1) ![]()
IQH state of composite fermion (which is an electron bound by two flux quanta)
(2) ![]()
IQH state of composite fermion (which is an electron bound by two flux quanta)
The effective magnetic field direction is opposite against the applied field.
(3) ![]()
IQH state of composite fermion (which is an electron bound by four flux quanta)
(4) ![]()
Combination state of the ![]() electron IQH state and the IQH state of composite fermion (which is a hole bound by four flux quanta)
electron IQH state and the IQH state of composite fermion (which is a hole bound by four flux quanta)
(5) ![]()
Combination state of the ![]() electron IQH state and the IQH state of composite fermion (which is an electron bound by four flux quanta)
electron IQH state and the IQH state of composite fermion (which is an electron bound by four flux quanta)
(6) ![]()
Combination state of the ![]() electron IQH state and the IQH state of composite fermion (which is a hole bound by two flux quanta)
electron IQH state and the IQH state of composite fermion (which is a hole bound by two flux quanta)
(7) ![]()
Combination state of the ![]() electron IQH state and the IQH state of composite fermion (which is a hole bound by two flux quanta)
electron IQH state and the IQH state of composite fermion (which is a hole bound by two flux quanta)
The effective magnetic field direction is opposite against the applied field.
(8) ![]()
Combination state of the ![]() electron IQH state and the IQH state of composite fermion (which is a hole bound by four flux quanta)
electron IQH state and the IQH state of composite fermion (which is a hole bound by four flux quanta)
We examine the composite fermion states for the five examples with![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() .
.
1) FQH state at ![]()
In the article [31] the ![]() FQH state is constructed by combining the
FQH state is constructed by combining the ![]() IQH state with the composite fermion state of hole for
IQH state with the composite fermion state of hole for ![]() as in Figure 15. Therein the black dots on the green sheet indicate the electrons in the
as in Figure 15. Therein the black dots on the green sheet indicate the electrons in the ![]() IQH state. The composite fermions of hole are expressed by the white circles on the yellow sheet, each of which is bound with two flux quanta as in Figure 15.
IQH state. The composite fermions of hole are expressed by the white circles on the yellow sheet, each of which is bound with two flux quanta as in Figure 15.
The effective magnetic field is expressed by the red arrows, the direction of which is opposite against the applied magnetic field. The total filling factor is the sum of ![]() and
and![]() . Accordingly the filling factor of electrons becomes
. Accordingly the filling factor of electrons becomes![]() .
.
2) FQH state at ![]()
The ![]() FQH state is explained by the combination of the
FQH state is explained by the combination of the ![]() IQH state and the composite fermion
IQH state and the composite fermion
state of hole with![]() . Each hole is bound with two flux quanta and the effective magnetic field is parallel to the applied magnetic field as shown in Figure 16.
. Each hole is bound with two flux quanta and the effective magnetic field is parallel to the applied magnetic field as shown in Figure 16.
3) FQH state at ![]()
The ![]() FQH state is produced by combining the
FQH state is produced by combining the ![]() IQH state with the composite fermion state with
IQH state with the composite fermion state with![]() . Therein the electron of the
. Therein the electron of the ![]() IQH state is expressed by the black circles on the sky-blue sheet in Figure 17. The residual electrons are expressed by the blue dots on the pink sheet, each of which is bound by the four flux quanta as seen in Figure 17 schematically. That is to say, some electrons are unbound with magnetic flux quanta and the other electrons are bound with flux quanta. However all the electrons exist in the same conducting thin layer and their wave functions are overlapping with each other. Furthermore in the many-body problem all the wave functions of electrons should satisfy the anti-symmetric relation. Also all the electrons should be affected by the same magnetic field. Accordingly the combination of the
IQH state is expressed by the black circles on the sky-blue sheet in Figure 17. The residual electrons are expressed by the blue dots on the pink sheet, each of which is bound by the four flux quanta as seen in Figure 17 schematically. That is to say, some electrons are unbound with magnetic flux quanta and the other electrons are bound with flux quanta. However all the electrons exist in the same conducting thin layer and their wave functions are overlapping with each other. Furthermore in the many-body problem all the wave functions of electrons should satisfy the anti-symmetric relation. Also all the electrons should be affected by the same magnetic field. Accordingly the combination of the ![]() IQH state and the
IQH state and the ![]() composite fermion state has some difficulty.
composite fermion state has some difficulty.
4) FQH state at ![]()
The ![]() FQH state is created by combining the
FQH state is created by combining the ![]() IQH state with the composite fermion state of hole for
IQH state with the composite fermion state of hole for ![]() as illustrated in Figure 18.
as illustrated in Figure 18.
Therein the black dots on the green sheet indicate the electrons in the ![]() IQH state. The composite fermions of hole are expressed by the white circles on the yellow sheet, each of which is bound with four flux quanta as seen in Figure 18.
IQH state. The composite fermions of hole are expressed by the white circles on the yellow sheet, each of which is bound with four flux quanta as seen in Figure 18.
5) FQH state at ![]()
The ![]() FQH state is produced by combining the
FQH state is produced by combining the ![]() IQH state with the composite fermion state of hole with
IQH state with the composite fermion state of hole with![]() . Therein the electron of the
. Therein the electron of the ![]() IQH state is expressed by the black circles on the sky- blue sheet in Figure 19. The composite fermions of hole are expressed by the white circles on the yellow sheet, each of which is bound by the four flux quanta.
IQH state is expressed by the black circles on the sky- blue sheet in Figure 19. The composite fermions of hole are expressed by the white circles on the yellow sheet, each of which is bound by the four flux quanta.
Thus the composite fermion theory uses many different kinds of quasi-particles and different directions of the effective magnetic field. When the filling factor varies by adjusting the gate voltage (or the applied magnetic field strength), the quasi-particle changes from hole to electron, the number of the bound flux-quanta changes, and the direction of the effective magnetic field changes from parallel to anti-parallel. These complicated assumptions are too artificial.
The quantum Hall system is originally described by the same Hamiltonian for all the filling factors. Therefore it is necessary that the FQHE is derived only from the original Hamiltonian by using the normal electrons and the usual quantum physics without any quasi-particle. This article succeeds to explain the FQHE which is produced by the abrupt change of the quantum-transition number. The abrupt change is caused by the momentum conservation, the most uniform configuration of electrons and the Fermi statistics.
7. Summary
The Hall resistance confinement is observed in the measurement of the current and the Hall voltage. In the real experiment, the Hall voltage is extremely large in comparison with the potential voltage. The ratio of (Hal voltage)/(potential voltage) is larger than 109 for the IQHE. Also the ratio is very large for the FQHE. That is to say, we cannot ignore the electric potential gradient in the direction of Hall voltage. Almost all the theories of FQHE neglect this electric potential gradient and use the symmetric property for the x- and y-directions on the 2D-electron plain. We have examined the eigen-states of single electron under the electric potential with the gradient. Then we have obtained the most uniform configuration of electrons in the Landau orbitals, the states of which satisfy the eigen-equation of the Hamiltonian (8). The Coulomb interaction produces the quantum transitions of electron pair (not single electron), because the interaction acts between two electrons. Therefore the total momentum along the current direction conserves between before and after transitions. Fermi statistics of electrons create abrupt change in the number of the allowed transitions for varying of the filling factor. This abrupt change produces an energy gap which yields the confinement of the Hall resistance at the specific fractional filling factors. This article and the previous works have clarified these mechanisms. The results are in a good agreement with the experimental data.
Acknowledgements
The author expresses his heartfelt appreciation for the encouragement of Professor Koichi Katsumata, Professor Masayuki Hagiwara, Professor Hidenobu Hori, Professor Yasuyuki Kitano and Professor Takeji Kebukawa. I cannot complete this article without their support.