One Dimensional Relativistic Free Particle in a Quadratic Dissipative Medium ()
1. Introduction
It is well known that the Lagrangian and Hamiltonian approaches for some non-dissipative and some dissipative systems have some problems [1] -[6] . One of these problems consists of the possibility of having two different Hamiltonian to the same classical system [7] , implying that one will have two different quantizations for this system. Another problem consists that for some dissipative non-relativistic systems, like a free particle moving in a dissipative medium characterized by a force which depends on the square of the velocity of the particle, the trajectories on the space  have an odd behavior. However, the trajectories on the space
have an odd behavior. However, the trajectories on the space , defined by the constant of motion, have a good expected behavior [8] . Nevertheless, the interest in having Hamiltonian for dissipative system continues [9] [10] .
, defined by the constant of motion, have a good expected behavior [8] . Nevertheless, the interest in having Hamiltonian for dissipative system continues [9] [10] .
In this work, the study of this former problem is extended to the relativistic motion of the particle. The constant of motion, the Lagrangian, and the Hamiltonian are deduced consistently, and it is shown that the behaviors of the trajectories of the particle in the phase space 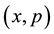 are odd when the Hamiltonian approach is used. However, the trajectories in the space
are odd when the Hamiltonian approach is used. However, the trajectories in the space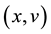 , when the constant of motion is used, behave as one can expected .
, when the constant of motion is used, behave as one can expected .
2. Constant of Motion, Lagrangian and Hamiltonian
The one-dimensional motion of a relativistic particle of mass “m” at rest which is moving with a velocity  in a dissipative medium characterized by a force which depends on the square of this velocity is described by the equation
in a dissipative medium characterized by a force which depends on the square of this velocity is described by the equation
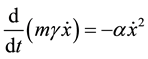 , (1)
, (1)
where 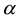 is the dissipative parameter,
is the dissipative parameter,  is the speed of light, and
is the speed of light, and 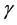 is the relativistic factor,
is the relativistic factor, .
.
Actually, Equation (1) represents a dissipative system for , otherwise it represents an anti-dissipative system. Therefore, only the case
, otherwise it represents an anti-dissipative system. Therefore, only the case 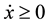 will be considered below. This system can be written as the following dynamical system
will be considered below. This system can be written as the following dynamical system
 . (2)
. (2)
A constant of motion for this system is a function 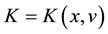 such that it satisfies the following partial differential equation of first order [11]
such that it satisfies the following partial differential equation of first order [11]
![]() . (3)
. (3)
The general solution of this equation [12] is given by![]() , where
, where ![]() is an arbitrary function of the characteristic curve
is an arbitrary function of the characteristic curve![]() ,
,
![]() . (4)
. (4)
By choosing![]() , a constant of motion is gotten with energy units,
, a constant of motion is gotten with energy units,
![]() . (5)
. (5)
The Lagrangian of the system can be consistently deduced from the known expression
![]() , (6)
, (6)
which establishes the relation between the Lagrangian and the constant of motion of the system [13] - [16] . Using this expression it follows that
![]() . (7)
. (7)
The generalized linear momentum, ![]() , is given by
, is given by
![]() . (8)
. (8)
The plot of this expression and the plot of the usual relativistic free linear momentum expression
![]() are shown in Figure 1, where one sees that for Equation (8) there is not a one to one
are shown in Figure 1, where one sees that for Equation (8) there is not a one to one
relation between the velocity ![]() and the generalized linear momentum
and the generalized linear momentum ![]() of Equation (8).
of Equation (8).
![]()
Figure 1. Relation between the generalized linear momentum and velocity.
The inverse relation of Equation (8) is shown on Figure 2, which is given analytically by
![]() , (9a)
, (9a)
and
![]() . (9b)
. (9b)
These expressions define respectively the Hamiltonians ![]() and
and ![]() as
as
![]() , (10a)
, (10a)
and
![]() . (10b)
. (10b)
3. Trajectories
Using the initial conditions![]() , with
, with ![]() and
and![]() , the constant of motion (5) is determined and the trajectories on the space
, the constant of motion (5) is determined and the trajectories on the space ![]() can be calculated. Figure 3 shows these trajectories for several values of the
can be calculated. Figure 3 shows these trajectories for several values of the
![]()
Figure 2. Inverse relation between the generalized linear momentum and velocity.
![]()
Figure 3. Trajectories in the (x,v) space, defined by the con- stant of motion.
parameter![]() . As one can see, the falling down of these trajectories and the way they are falling as the para- meter
. As one can see, the falling down of these trajectories and the way they are falling as the para- meter ![]() increases represent the behavior that one can expected for a dissipative medium. Now, given these same initial conditions, the initial generalized linear momentum is calculated from expression (8). One uses the expression (10a) to determinate the value of this Hamiltonian and to calculated the trajectories in the space
increases represent the behavior that one can expected for a dissipative medium. Now, given these same initial conditions, the initial generalized linear momentum is calculated from expression (8). One uses the expression (10a) to determinate the value of this Hamiltonian and to calculated the trajectories in the space![]() . These trajectories can be seen in Figure 4. As one can see, these trajectories have an odd behavior since
. These trajectories can be seen in Figure 4. As one can see, these trajectories have an odd behavior since ![]() go to infinity as the particle is slowing down, but this was already expected from the same expression for the generalized linear momentum, Equation (8).
go to infinity as the particle is slowing down, but this was already expected from the same expression for the generalized linear momentum, Equation (8).
4. Conclusion
We have constructed consistently a constant of motion, Lagrangian, and Hamiltonian for a relativistic particle moving in a dissipative medium, characterized by a force which depends on the square velocity of the particle.
![]()
Figure 4. Trajectories in the (x,p) space, defined by the Hamil- tonian.
The trajectories in the space![]() , defined by the constant of motion, behave as we can expect. However, the trajectories in the space
, defined by the constant of motion, behave as we can expect. However, the trajectories in the space![]() , defined by the Hamiltonian, behave oddly and totally anti-intuitively. This suggests that the Hamiltonian approach applied to dissipation problem may bring about incorrect solutions if it is directly applied to quantum mechanics or statistical physics.
, defined by the Hamiltonian, behave oddly and totally anti-intuitively. This suggests that the Hamiltonian approach applied to dissipation problem may bring about incorrect solutions if it is directly applied to quantum mechanics or statistical physics.