Correct Classification Rates in Multi-Category Discriminant Analysis of Spatial Gaussian Data ()
1. Introduction
Much work has been done concerning the error rates in two-category discrimination of uncorrelated observations (see e.g. [1] ). Several methods for estimations of the error rates in discriminant analysis of spatial data have been recently proposed (see e.g. [2] [3] ).
The multi-category problem, however, has very rarely been addressed because most of the methods proposed for two categories do not generalize. Schervish [4] considered the problem of classification into one of three known normal populations by single linear discriminant function. Techniques for multi-category probability estimation by combining all pairwise comparisons are investigated by several authors (see e.g. [5] ). Empirical comparison of different methods of error rate estimation in multi-category linear discriminant analysis for multivariate homoscedastic Gaussian data was performed by Hirst [6] . Bayesian multiclass classification problem for correlated Gaussian observation was empirically studied by Williams [7] . The novel model-free estimation method for multiclass conditional probability based on conditional quintile regression functions is theoretically and numerically studied by Xu [8] . Correct classification rates in multi-category classification of independent multivariate Gaussian observations were provided by Schervish [9] . We generalize results of above to the problem of classification of multivariate spatially correlated Gaussian observations.
We propose the method of multi-category discriminant analysis essentially exploiting the Bayes classification rule that is optimal in the sense of minimum misclassification probability in case of complete statistical certainty (see [10] , chapter 6). In practice, however, the complete statistical description of populations is usually not possible. Then having training sample, parametric plug-in Bayes classification rule formed by replacing unknown parameters with their estimators in BCR is being used.
Šaltytė and Dučinskas [11] derived the asymptotic approximation of the expected error rate when classifying the observation of a scalar Gaussian random field into one of two classes with different regression mean models and common variance. This result was generalized to multivariate spatial-temporal regression model in [12] . However, the observations to be classified are assumed to be independent from training samples in all publication listed above. The assumption of independence for the classification of scalar GRF observations was removed by Dučinskas [2] . Multivariate two-category case has been considered in Dučinskas [13] and Dučinskas and Dreižienė [14] . Formulas for the error rates for multiclass classification of scalar GRF observation are derived in [15] . The authors of the above papers have been focused on the maximum likelihood (ML) estimators because of tractability of the covariance matrix of these estimators. In the present paper, we extend the investigation of the performance of the PBCR in multi-category case. The novel closed form expressions for the actual correct classification rate (ACCR) are derived.
By using the derived formulas, the performance of the PBR is numerically analyzed in the case of stationary Gaussian random field on the square lattice with the exponential covariance function. The dependence of the correct classification rate and ACCR values on the range parameter is investigated.
The rest of the paper is organized as follows. Section 2 presents concepts and notions concerning BCR applied to multi-category classification of multivariate Gaussian random field (MGRF) observation. Bayes probability of correct classification is derived. In Section 3, the actual correct classification rate incurred by PBCR is considered and its closed-form expression is derived. Numerical examples, based on simulated data, are presented in Section 4, in order to illustrate theoretical results. The effect of the values of range parameter on the values of ACCR is examined.
2. The Main Concepts and Definitions
The main objective of this paper is to classify a single observation of MGRF 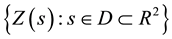 into one of
into one of  categories, say
categories, say .
.
The model of observation 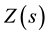 in category
in category 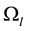
 is
is
 .
.
Here 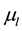 represents a mean component and
represents a mean component and 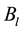 is a matrix of parameters. The error term is generated by p-dimensional zero-mean stationary GRF
is a matrix of parameters. The error term is generated by p-dimensional zero-mean stationary GRF 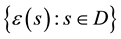 with covariance function defined by model for all
with covariance function defined by model for all 
 ,
,
where 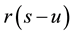 is the spatial correlation function and
is the spatial correlation function and 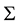 is the variance-covariance matrix with elements
is the variance-covariance matrix with elements . So we have deal with so called intrinsic covariance model (see [16] ).
. So we have deal with so called intrinsic covariance model (see [16] ).
Consider the problem of classification of the vector of observation of 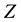 at location
at location ![]() denoted by
denoted by ![]() into one of
into one of ![]() populations specified above with given joint training sample
populations specified above with given joint training sample![]() . Joint training sample
. Joint training sample ![]() is stratified training sample, specified by
is stratified training sample, specified by ![]() matrix
matrix![]() , where
, where ![]() is the
is the ![]() matrix of
matrix of ![]() observations of
observations of ![]() from
from![]() ,
, ![]() ,
,![]() .
.
Then the model of ![]() is
is
![]() ,
,
where ![]() is the matrix of category means parameters and
is the matrix of category means parameters and ![]() is the
is the ![]() matrix of random errors that has matrix-variate normal distribution i.e.
matrix of random errors that has matrix-variate normal distribution i.e.
![]() .
.
Here ![]() denotes the spatial correlation matrix among components (rows) of
denotes the spatial correlation matrix among components (rows) of![]() . In the rest of the paper the realization (observed value) of training sample
. In the rest of the paper the realization (observed value) of training sample ![]() will be denoted by
will be denoted by![]() .
.
Denote by ![]() the vector of spatial correlations between
the vector of spatial correlations between ![]() and observations in
and observations in ![]() and set
and set![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
Notice that in category![]() , the conditional distribution of
, the conditional distribution of ![]() given
given ![]() is Gaussian, i.e.
is Gaussian, i.e.
![]() ,
,
where conditional means ![]() are
are
![]() (1)
(1)
and conditional covariance matrix ![]() is
is
![]() . (2)
. (2)
The marginal and conditional squared Mahalanobis distances between categories ![]() and
and ![]()
![]() for observation taken at location
for observation taken at location ![]() are specified respectively by
are specified respectively by
![]() ,
,
and
![]() .
.
It is easy to notice that ![]() does not depend on realizations of
does not depend on realizations of ![]() and depends only on their locations.
and depends only on their locations.
Under the assumption of completely parametric certainty of populations and for known prior probabilities of populations![]() ,
, ![]() , Bayes rule minimizing the probability of misclassification is based on the logarithm of the conditional densities ratio.
, Bayes rule minimizing the probability of misclassification is based on the logarithm of the conditional densities ratio.
There is no loss of generality in focusing attention on category![]() , since the numbering of the categories is arbitrary. Let the set of population parameters is denoted by
, since the numbering of the categories is arbitrary. Let the set of population parameters is denoted by![]() . Set
. Set![]() .
.
Denote the log ratio of conditional densities in categories ![]() and
and ![]() by
by
![]() , (3)
, (3)
where![]() ,
,![]() .
.
These functions will be called pairwise discriminant functions (PDF).
Then Bayes rule (BR) (see [10] , chapter 6) is given by:
classify ![]() to population
to population ![]() if for
if for![]() ,
,![]() . (4)
. (4)
3. Probabilities and Rates of Correct Classification
Set ![]() and set
and set ![]() as
as ![]() -dimensional vector with the l-th components
-dimensional vector with the l-th components ![]() specified as
specified as![]() , and
, and ![]() with
with![]() .
.
Lemma 1. The conditional probability of correct classification for category ![]() due to BCR specified in (4) is
due to BCR specified in (4) is
![]() .
.
Here ![]() is the probability density function of r-variate normal distribution with mean vector
is the probability density function of r-variate normal distribution with mean vector ![]() and variance-covariance matrix
and variance-covariance matrix![]() .
.
Proof. Recall, that under the definition (see e.g. [4] [9] ) a probability of correct classification due to aforementioned BCR is
![]() . (5)
. (5)
It is the probability of correct classification of ![]() when it comes from
when it comes from![]() . Probability measure
. Probability measure ![]() is based on conditional distribution of
is based on conditional distribution of ![]() given
given![]() ,
, ![]() with means and variance-covariance matrix specified in (1), (2).
with means and variance-covariance matrix specified in (1), (2). ![]() may be expressed in form
may be expressed in form
![]() ,
,
where![]() , and
, and ![]() denotes the
denotes the ![]() dimensional identity matrix.
dimensional identity matrix.
After making the substitution of variables ![]() in (5) we obtain that
in (5) we obtain that
![]() and
and![]() ,
,![]() .
.
Set![]() , then probability of correct classification can be rewritten in the following way
, then probability of correct classification can be rewritten in the following way![]() .
.
After straightforward calculations we show that![]() . That completes the proof of lemma.
. That completes the proof of lemma.
In practical applications not all statistical parameters of populations are known. Then the estimators of unknown parameters can be found from training sample. When estimators of unknown parameters are plugged into Bayes discriminant function (BDF), the plug-in BDF is obtained (PBDF). In this paper we assume that true values of parameters ![]() and
and ![]() are unknown.
are unknown.
Let ![]() and
and ![]() be the estimators of
be the estimators of ![]() and
and ![]() based on
based on![]() . Set
. Set![]() .
.
Then replacing ![]() by
by ![]() in (3) we get the plug-in BDF (PBDF)
in (3) we get the plug-in BDF (PBDF)
![]() .
.
Then the classification rule based on PBCR is associated with plug-in PDF (PPDF) in the following way: classify ![]() to population
to population ![]() if for
if for ![]()
![]() .
.
Definition 1. The actual correct classification rate incurred by PBCR associated with PPDF is
![]() .
.
Set ![]() and
and![]() .
.
Lemma 2. The actual correct classification rate due to PBDR is
![]() ,
,
where ![]() is r-dimensional vector with components
is r-dimensional vector with components![]() ,
, ![]() and
and![]() .
.
Proof. It is obvious that in population ![]() the conditional distribution of BPDF
the conditional distribution of BPDF ![]() given
given ![]() is Gaussian, i.e.,
is Gaussian, i.e.,
![]() .
.
Set![]() , then probability of correct classification can be rewritten in the following way:
, then probability of correct classification can be rewritten in the following way:
![]() .
.
After straightforward calculations we show that![]() . That completes the proof of lemma.
. That completes the proof of lemma.
4. Example and Discussions
Simulation study in order to compare proposed Bayes probability of correct classification rate and the actual correct classification rate incurred by PBCR was carried out for three class case![]() . Also the effect of the range parameter on these values is examined.
. Also the effect of the range parameter on these values is examined.
In this example, observations are assumed to arise from bivariate stationary Gaussian random field ![]() with constant mean and isotropic exponential correlation function given by
with constant mean and isotropic exponential correlation function given by![]() , where
, where ![]() is a parameter of spatial correlation (range).
is a parameter of spatial correlation (range).
Set![]() ,
, ![]() and
and![]() .
.
Estimators of ![]() and
and ![]() have the following form:
have the following form:
![]() ,
,
where ![]() denotes design matrix of training sample
denotes design matrix of training sample ![]() and is specified by
and is specified by ![]() and
and
![]() .
.
Considered set of training locations with indicated class labels is shown in Figure 1.
So we have small training sample sizes (i.e.![]() ) and three different locations to be classified, furthermore we assume equal prior probabilities
) and three different locations to be classified, furthermore we assume equal prior probabilities![]() ,
,![]() .
.
Simulations were performed by geoR: a free and open-source package for geostatistical analysis included in statistical computing software R (http://www.r-project.org/). Each case was simulated 100 times (runs) and ![]() values are calculated by averaging ACCR over the runs.
values are calculated by averaging ACCR over the runs. ![]() and CCR values are presented in Table 1. As might be expected
and CCR values are presented in Table 1. As might be expected ![]() values are lower than CCR. All values are increasing while range parameter is increasing. That means the stronger correlation gives better accuracy of proposed classification procedures.
values are lower than CCR. All values are increasing while range parameter is increasing. That means the stronger correlation gives better accuracy of proposed classification procedures.
![]()
Figure 1. Locations of training sample: “1” are samples from population Ω1, “2” from Ω2, “3” from Ω3, A, B and C denotes the locations of observation to be classified.
It’s seen in Figure 1, that the closest location to be classified is location A and the farthest is location C. CCR and ![]() are largest for location A and smallest for location C. It can be concluded that better accuracy gives closer locations.
are largest for location A and smallest for location C. It can be concluded that better accuracy gives closer locations.