Comparison of Four Methods for Handing Missing Data in Longitudinal Data Analysis through a Simulation Study ()
1. Introduction
The problem of missing observations can frequently occur in all types of clinical trials, especially when observations are measured repeatedly at each scheduled visit for the same subject in a longitudinal study. In longitudinal studies, there are many possible causes leading to missing data including the duration of the study, the nature of the disease, the efficacy and adverse effects of the drug under study, accidents, patients’ refusal to continue, moving, or other administrative reasons. Frequently, missingness can potentially lead to two serious problems in statistical practice: reducing the overall statistical power and having biases in the estimates. In statistical practice, missing data is a key problem that can never be avoided completely. Since the most traditional statistical methods are intentionally designed to handle complete data sets by default, therefore data analysts should pay special attention to incomplete data sets.
Little and Rubin [1] have classified missing data mechanisms into three different types based on the possible causes: 1) missing completely at random (MCAR) if the missingness is not related to any observed and unobserved factors (such as domestic relocation, suffering an accident, or unrelated illness); 2) missing at random (MAR) if the missingness is conditional on observed factors and is independent of the unobserved data (such as lack of efficacy); and 3) missing not at random (MNAR) if the missingness depends on unobserved quantities as well as some observed factors. The MNAR missing mechanism is usually used to describe patients who may drop out as a result of health deterioration related to the treatments that we do not have a chance to observe because of their dropout. Researchers have pointed out that the MAR assumption may be more plausible in practice than that of the MCAR [2] . In fact, by definition MCAR is only a special case of MAR. In other words, a MCAR missing mechanism is also a MAR one, but not every MAR is a MCAR. Actually, it is possible to formally test the MCAR assumption against its alternative hypothesis not MCAR [3] [4] . However, it is not possible to test MAR or MNAR without using additional (external) information. MNAR is particularly useful in assessing the sensitivity of the results that are not MAR [5] and it is highly recommended to be incorporated into the analysis.
In the literature, several alternative statistical approaches have been applied to the analysis of longitudinal data with missing values. These appropriate methods for analysis should be selected based on the data missing mechanism, since different statistical methods are valid only under certain situations (missing mechanisms) with specified missing rates. In other words, there is no unique best method available for all situations. However, it is difficult to test the missing mechanism in a longitudinal clinical study and there is also no clear rules regarding how much is qualified as too much missing data [6] . In general, the choice of a particular method for handling missing data depends largely on whether one is considering a more pragmatic or a more explanatory perspective. There is often the question of whether there are too many missing data. Sprint and Dupin-Sprint [7] pointed out that the tolerable amount of missing data is that would not conceal an effect in the opposite direction. In order to determine whether this level of missing data has been reached, one can perform what was called the “worst case” analysis.
Despite these difficulties, several researchers have considered and constructed simulation studies for the proof of strong consistency of imputation methods to check the efficiency of the imputation methods. For example, Myers [8] compared the results of two imputation methods (that is, the complete case method and the multiple imputation method) based on simulated data sets with a dropout rate ranging from 20% to 60%, and they concluded that MI method provided results that are more closely mimicked the complete data set.
Hening and Koonce [9] investigated five imputation methods (i.e., mean substitution, median substitution, zero value, hot-deck, and MI) and a first-year-student retention data with more than 20% missing values is used. The results shown that multiple and hot-deck imputations perform poorly in an accuracy comparison test, but they can slightly increase the predication accuracy rate compared with other methods.
Ali, et al. [10] performed a survival analysis in which missing data were simulated under MCAR and MAR to compare four imputation methods?complete case analysis (CCA), means substitution (MS), and multiple imputation (MI)with the inclusion of the outcome (MI− and MI+). The simulation results suggested that in general MI+ is likely to be the best method. Patrician [11] pointed out that MI is the best approach and should be considered to handle missing data compared with CCA and MS by an empirical investigation of AIDS care longitudinal data outcomes.
Recently, Nakai, et al. [12] have shown that MI is the most effective imputation method in longitudinal data setting under MCAR via a simulation study. This indeed provides useful information about the performance of imputation methods under MCAR, but it is limited and restricted to clinical situations where MAR is more plausible. For example, Lavori, et al. [13] have pointed out that the MCAR assumption is often not plausible in most clinical trial settings. The purpose of this paper is through a simulation approach to analytically evaluate the performance of four imputation methods for different missing mechanisms (MCAR and MAR) with various missing rates. For simplicity and also without loss of generality, a monotone pattern of missing data (meaning that once a patient has a missing response at an assessment visit, his or her data will be missing for all subsequent visits) is assumed. Under such assumptions, this paper primarily concentrates on the following four imputation methods: 1) complete case (CC); 2) mean substitution (MS); 3) last observation carried forward (LOCF); and 4) multiple imputation (MI). To compare the performance of these methods, bias, RMSE, and 95% coverage probability (CP) of the estimated parameters are used as evaluation criteria.
This paper is organized as follows. Section 2 reviews methods of missing data analysis. The simulation procedures (with available covariates) under MCAR and MAR settings are described in Section 3. In Section 4, the simulation results are used to evaluate the performance of those four imputation methods considered. Finally, discussion and concluding remarks are provided in Section 5.
2. Approaches to Handling Missing Data
There are so many techniques in handling missing data discussed in the literature. Especially, many methods have been proposed and developed to handle missing data in longitudinal clinical trials. However, there are few methods that are actually used in real trials with missing data. The purpose of this paper is to study four most frequently used methods for dealing with missing data and they will be described as follows.
2.1. Complete Case (CC) Analysis
This method deletes all cases with missing data and then performs statistical analyses on the remaining complete data set (which has a smaller sample size). Since all cases containing missing data have been removed, there is no missing data problem to handle. Therefore, all statistical methods can be used to analyze the smaller data set. Obviously, one major advantage of this method is its ease of use. In fact, virtually all statistical programs incorporate this method as a default method because it accommodates any type of statistical analysis [14] . The method may be preferred under the situation in which the sample size is large, the proportion of missing data is small, and the missing data mechanism is MCAR [15] . For MCAR missing data, the method will yield unbiased parameter estimates and larger standard errors due to the smaller sample size. However, even when data are MCAR, loss of data will result in loss of precision (larger standard errors), particularly in multivariate data analyses.
In general, the major disadvantage of the method is that it could possibly lead to losing statistical power due to the reduction of the sample size. Also, complete case techniques erode efficiency such that the variation (i.e., the standard error) around the true estimate is too large [16] . In addition, if data are not MCAR, bias can be a serious issue [17] - [19] .
2.2. Mean Substitution (MS)
The method of mean substitution imputes the missing values using the mean of the available observed values. This method has the potential of introducing biases as well as underestimating variability [20] - [22] . This method has the advantage of being able to maintain the original sample size while it also allows one to use the complete- data methods for data analysis [23] . However, due to the reduced variability, the estimated parameters are less precise. Decreased variances are problematic because the resulting estimates are too close to the mean [24] .
2.3. Last Observation Carried Forward (LOCF)
The simplest imputation approach is the LOCF method that replaces every missing value with its corresponding last observed value. LOCF method is often used in longitudinal studies of continuous outcomes under MCAR. Conceptually, this method assumes that the outcome would not change after the last observed value. Therefore, there is no time effect since the last observed data. In fact, LOCF has been a popular method that is frequently used in handling missing data problems because it is easy to understand and can be implemented easily as well. Also, unlike the CC method, the sample size does not change. For example, in a clinical trial (see the data below), patient 3 dropped out from the study after baseline. Patient 6 dropped out after the first month follow up.
?: missing value; *: value imputed by LOCF.
If there are more patients dropped out in the placebo group due to the lack of efficacy, then this method might give a biased conclusion about the effect of the treatment group. In general, the measurements are unlikely to remain unchanged for either placebo or treatment group. In our example, the measurement of patient 3 from the control group will increase while that of patient 6 from the active group will decrease. This implies that there is no improvement in the active group and hence no difference between these two groups.
Rigorously speaking, LOCF is not an analytic approach, but it is a method that is very easy to impute missing values. Analytic proofs [25] [26] and studies in simulated data [26] - [29] have been clearly shown that LOCF can bias results and lead to either overestimation or underestimation of the parameter estimates.
2.4. Multiple Imputation (MI)
Multiple imputation was first proposed by Rubin [23] [30] to analyze incomplete data under the MAR missing mechanism. Allison [14] and Schafer [31] [32] further explained Rubin’s MI. MI is a predictive approach to handling missing data in multivariate analysis and blends both classical and Bayesian statistical techniques. The idea of MI is to impute a missing value multiple times and hence generates multiple (m) data sets. Missing data theorists have claimed that good inferences can be made for only 3 - 5 imputed data sets [33] . Others have suggested that the number of imputed data sets should approximate the percentage of subjects with some missing data [34] . In this paper, 100 imputed data sets are used because there is a 50% missing rate in Case 3 of the simulation study. Then, these imputed data sets are analyzed by standard procedures that are commonly used in analyzing complete data sets. Finally, the results of analyses are combined [35] [36] . A few assumptions and constraints of MI are: 1) missing data mechanism should be MAR; 2) the imputation model must match the analysis model [14] ; and 3) the algorithm used to generate imputed values must accommodate/include the variables associated with the missingness of the data as well as other related variables. Allison [37] illustrated that good imputation methods use all information related to missing cases. Two major advantages of MI are allowing the use of complete-data methods for data analysis and incorporating random errors in the imputation process. MI can accommodate any model with any data and does not require specialized software. In addition, MI increases efficiency of the estimates through minimizing the standard errors [23] . However, Rubin [23] pointed out that the three disadvantages of MI are more effort to create the multiple imputations, more time to run the analyses, and more computer storage space for the imputation-created data sets.
3. Simulations
We conducted a simulation study on different scenarios. In general, generating each dataset is based on the setting described in Section 3.1 by the following assuming: 1) the measurement at the first time point (t = 1) from the original data is completely observed; 2) data are MCAR and MAR missing mechanisms; 3) the missing pattern is monotone. To begin the simulated process, the first step (1-step) generates the five-time points of measurements of each subject by a random number from a multivariate normal distribution with AR(1) correlation structure and repeats the step 100 times for 100 subjects, given the observed values,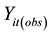 ;
;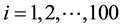 ; and
; and . The second step (2-step) is to generate the MCAR and MAR data,
. The second step (2-step) is to generate the MCAR and MAR data,  , as described in Section 3.3 by the missing rate (%) at each time point measurement in Table 1. The third step is to test the MCAR and MAR condition using Little’s MCAR test to check whether the produced datasets are MCAR and MAR or not.
, as described in Section 3.3 by the missing rate (%) at each time point measurement in Table 1. The third step is to test the MCAR and MAR condition using Little’s MCAR test to check whether the produced datasets are MCAR and MAR or not.
![]()
Table 1. Detailed design of the simulation.
Finally, each of the predefined 9 situations was repeated 1000 times by using SAS procedures. There are 1000 data sets each containing 100 subjects with 5 time points per subject to be analyzed. Next, the standard mixed model procedures were performed on these simulated data sets. Finally, the regression coefficients and their standard errors were obtained. Then, the performance of four selected methods (that is, complete case analysis, mean substitution, last observation carried forward, and multiple imputation) was compared based on biases, root mean square errors, and 95% coverage probabilities. In the simulation, we considered the missing data with MCAR and MAR missing mechanisms. In addition, without loss of generality, the missing pattern was assumed to be monotone. The missing rate varied from 5% to 50%.
3.1. Background of the Simulation
In the simulation, we generated the longitudinal data 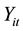 (
(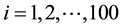 ;
; ) for the ith subject at the tth visit according to a multivariate normal distribution model,
) for the ith subject at the tth visit according to a multivariate normal distribution model, 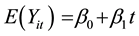 where β0 is the intercept and β1 is the slope. The variance at each occasion is assumed to be constant over time, while the correlation coefficient between
where β0 is the intercept and β1 is the slope. The variance at each occasion is assumed to be constant over time, while the correlation coefficient between 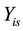 and
and 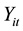 is assumed to be a positive correlation coefficient ρ of a first-order autoregressive model (i.e., AR(1)).
is assumed to be a positive correlation coefficient ρ of a first-order autoregressive model (i.e., AR(1)).
More precisely, a data set X with n rows and p columns is drawn from a multivariate normal distribution with a zero mean vector and a variance-covariance matrix 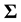 given as follows
given as follows
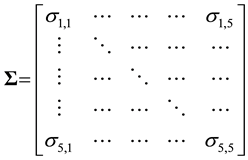
The correlation structure of an AR(1) model can be described as

where
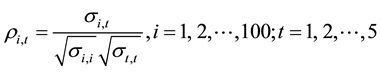
In this study, the correlation coefficient ρ is taken to be 0.7 to simulate the strong relationships among variables. The total number of cases (or subjects) is 100 and there are 5 measurements at 5 time points for each subject.
3.2. Design of the Simulation
Table 1 listed the values of parameters used in the simulation study. The value of the intercept was fixed at 10 while the value of the slope was 0.1, 2, or 10. The variance was chosen to be 1. And, the correlation coefficient was set to 0.7, where ρ = 0.7 is a typical value used to represent moderate to high correlation. Nakai (2014) used both ρ = 0.1 and ρ =
0.7 in
his study. However, he showed the results are not significantly different for both values of correlation coefficient. Three combinations of missing rates under both MCAR and MAR missing mechanisms were considered. (See Table 1 for details).
Therefore, in the simulation 1000 samples were generated covering 18 different situations: 3 (missing rates) × 3 (values of the slope) × 2 (missing mechanisms).
3.3. Missing Data Generation
The data were generated with situations described in Sections 3.1 and 3.2 and the measurements were drawn from a multivariate normal distribution with AR(1) correlation structure [12] . The data generating process was repeated 1000 times for each of 18 different situations. PROC IML of the SAS System (version 9.3) was used to generate these data sets. Hereafter, these simulated data sets (without any missing observation) are referred to as the “Original” data sets.
After the original data sets were created, the measurements at different time points for different subjects were set to missing, according to the MCAR or MAR missing mechanism. However, the measurement at the first time point (that is, the baseline value) of each subject was assumed always observed. In the MCAR setting, missing data were generated randomly at visits 2 through 5 based on the missing probabilities listed in Table 1. Therefore, the missing probabilities do not depend on either observed or unobserved data. Furthermore, Little’s MCAR test [3] was performed to make sure the missing mechanism is indeed MCAR otherwise that data set was discarded and another data set was generated anew.
In the MAR setting, the probability of missing at visit 2 was set in proportional to the baseline values based on a logistic probability distribution model. In the same way, the missing data at visits 3 through 5 were set based on the probabilities given in Table 1. In this way, the missing probabilities will depend only on observed data. Hence, the missing mechanism is under MAR mechanism by MAR definition. It was quite time-consum- ing in generating and analyzing these data sets. Actually, it would take almost a day to do such a job for a single simulation setting.
3.4. Measures of Performance for Imputation Methods
Bias, root mean squared error (RMSE), and coverage probability are used as criteria to assess the performance of the four imputation methods. The SAS System (version 9.3) is used to perform all the statistical analyses as well as to produce the required results. Also, we set covariance structure to “Unstructured” simply to explore the accuracy of imputation within “PROC MIXED” procedure. These criteria will be described in detail in the following subsections.
3.4.1
. Bias
Bias is defined as the difference between the average value of estimated parameters (![]() and
and![]() ) and the true parameters (β0 and β1) obtained from the corresponding original data set.
) and the true parameters (β0 and β1) obtained from the corresponding original data set.
3.4.2
. RMSE
The mean squared error (MSE) is defined as the average squared difference between the estimated parameters (![]() and
and![]() ) and the corresponding true parameters (β0 and β1) obtained from the original data set. MSE is equal to the sum of variance and the squared bias of the estimated parameters. RMSE is defined as the square root of the MSE. The RMSE is a useful measure of overall precision or accuracy and can be used to evaluate the performance of each imputation method. In general, the more effective method would have a lower RMSE [38] .
) and the corresponding true parameters (β0 and β1) obtained from the original data set. MSE is equal to the sum of variance and the squared bias of the estimated parameters. RMSE is defined as the square root of the MSE. The RMSE is a useful measure of overall precision or accuracy and can be used to evaluate the performance of each imputation method. In general, the more effective method would have a lower RMSE [38] .
3.4.3
. Coverage Probability
The coverage probability (CP) is defined as the proportion of the simulated data sets, among the 1000 simulated data sets, that yield the 95% confidence intervals containing the true parameter values based on the original data sets. Therefore, an appropriate method should have a coverage probability around 95%.
4. Simulation Results
The simulation results are summarized in Tables 2-7. In these table, CC, MS, LOCF, MI, MCAR, and MAR stand for complete case, mean substitution, last observation carried forward, multiple imputation, missing completely at random, and missing at random, respectively. Case 1, Case 2, and Case 3 represent the low, moderate, and high missing rate setting as given in Table 1. In the following tables, bold numbers are used to highlight the best method in that particular case.
4.1. Simulation Results for MCAR Missing Data
Tables 2-4 show the simulation results for MCAR (missing complete at random) data. The cases of low, moderate, and high missing rates are illustrated in Table 2, Table 3, and Table 4, respectively. In the low missing rate case (Table 2), except the LOCF method, the other three methods yield very small biases and RMSEs for both Intercept and Slope. In the case that the slope is 10, the 95% CPs are very poor for the LOCF method (100% and 0% for Intercept and Slope, respectively). In the moderate missing rate case (Table 3), the results are quite similar to that in the low missing rate case. However, the 95% CPs are poor for the LOCF method in both moderate and large slope cases. In the high missing rate case (Table 4), the 95% CPs are very poor for the LOCF method in both moderate and large slope cases. In summary, the bias and RMSE will increase with the increase of the missing rate. However, the biases are small except for the LOCF method. For a fixed missing rate, the bias and RMSE will increase with the increase of the slope value.
Based on the six performance criteria for MCAR missing data, the LOCF is the poorest method. The CC method is the best method. However, the MI method had the same performance as the CC method. The template is designed so that author affiliations are not repeated each time for multiple authors of the same affiliation. Please keep your affiliations as succinct as possible (for example, do NOT post your job titles, positions, academic degrees, zip codes, names of building/street/district/province/state, etc.). This template was designed for two affiliations.
![]()
Table 2. Performance of four methods for Case 1 and ρ = 0.7 (MCAR).
![]()
Table 3. Performance of four methods for Case 2 and ρ = 0.7 (MCAR).
![]()
Table 4. Performance of four methods for Case 3 and ρ = 0.7 (MCAR).
4.2. Simulation Results for MAR Missing Data
Tables 5-7 show the simulation results for MAR (missing at random) data. The cases of low, moderate, and high missing rates are illustrated in Table 5, Table 6, and Table 7, respectively. In the low missing rate case (Table 5), the biases for the CC and MS methods are slightly larger for Intercept but smaller for those of Slope. However, the bias for the LOCF method is slightly smaller for Intercept but larger for that of Slope. Again, in the case that the slope is 10, the 95% CPs are very poor for the LOCF method (100% and 0% for Intercept and Slope). Also, in the case that the slope is 2, the 95% CP is 41.4% for the LOCF method. Based on the six performance criteria, the MI method is the best in this case. In the moderate missing rate case (Table 6), the results are similar for the performance of the LOCF method. Again, the MI method yield smaller bias, RMSE, and good 95% CP. In the high missing rate case (Table 7), the 95% CPs are very poor for the LOCF method in both moderate and large
![]()
Table 5. Performance of four methods for Case 1 and ρ = 0.7 (MAR).
![]()
Table 6. Performance of four methods for Case 2 and ρ = 0.7 (MAR).
slope cases. In summary, the LOCF method yields larger biases, RMSEs, and poor 95% CPs in most cases. In contrast, the MI method performs much better than the other three methods under MAR mechanism.
5. Discussion and Conclusions
Although the simulation results suggested that the CC method was superior to the MS, LOCF, and MI methods under MCAR missing mechanism while MI method was superior to CC, MS, and MI methods under MAR, the performance of these methods actually depended on several factors especially the missing rate and time effect (that is, the size of the slope). However, there is no one single method that is the best under all situations.
Under the assumption of MCAR missing mechanism, when the missing rate increased from low to moderate (slope = 0.1 or 2), the values of estimated bias and RMSE for CC, MS, and MI methods were very close. Except
![]()
Table 7. Performance of four methods for Case 3 and ρ = 0.7 (MAR).
for high missing rate and large slope (that is, slope = 10), the values of bias and RMSE obtained by the MI method had large differences compared with those obtained by the CC and MS methods. This is not surprising at all because the CC method will yield unbiased estimated parameters under MCAR only with a small missing rate.
For the MAR missing data, the simulation results revealed that MI is the best method regardless of the missing rate and slope size based on bias, RMSE, and 95% CP. In fact, such a result is well documented in the literature [23] [31] . For low missing rate and small slope, the results did not differ significantly between the MI and LOCF methods. Such a result was also been discussed in the literature [39] [40] .
In this paper, we consider a longitudinal study with five visiting time points and a total of 100 subjects. Three possible missing rates and three different slopes are used to mimic the real-world situations. In addition, two missing mechanisms are considered (that is, MCAR and MAR).Based on the simulation results, we have reached the following important conclusions: 1) CC method is the most appropriate method for handling MCAR missing data; 2) MI method is the most effective one in all simulated situations particularly under MAR setting because it yields smallest biases and has good 95% CP compared with the other methods; 3) the use of the LOCF method can potentially lead to imprecise parameter estimates hence can lead to invalid inferences.
In practice, inferior methods such as LOCF are still used for the longitudinal data analysis. The results via the simulation dataare indeed provide a good reference and rationale in choosing missing data handling method in order to obtain precise parameter estimates and valid inferences. Kenward and Molenberghs [41] did suggest that LOCF method should be avoided which is well supported by our simulation results.
Acknowledgements
I would like to thank the reviewer for his/her valuable comments and suggestions that make this paper much better in its contents.