1. Introduction
The task of recovering the latent topics underlying a given corpus of documents has been in the forefront of active research in statistical machine learning for more than a decade, and continues to receive the dedicated contributions from many researchers from around the world. Since the introduction of Latent Dirichlet Allocation (LDA) [1] and then the extension to correlated topic models (CTM) [2] , a series of excellent contributions have been made to this exciting field, ranging from slight extension in the modelling structure to the development of scalable topic modeling algorithms capable of handling extremely large collections of documents, as well as selecting an optimal model among a collection of competing models or using the output of topic modeling as entry points (inputs) to other machine learning or data mining tasks such as image analysis and sentiment extraction, just to name a few. As far as correlated topic models are concerned, virtually all the contributors to the field have so far concentrated solely on the use of the logistic normal topic model. The seminal paper on correlated topic model [2] adopts a variational approximation approach to model fitting while subsequent authors like [3] propose a Gibbs sampling scheme with data augmentation of uniform random variables. More recently, [4] presented an exact and scalable Gibbs sampling algorithm with Polya-Gamma distributed auxiliary variables which is a recent development of efficient sampling of logistic model. Despite the inseparable relationship between logistic and probit model in statistical modelling, the probit model has not yet been proposed, probably due to its computational inefficiency for multiclass classification problem and high posterior dependence between auxiliary variables and parameters. As for practical application where topic models are commonly employed, having multiple topics is extremely prevalent. In some cases, more than 1000 topics will be fitted to large datasets such as Wikipedia and Pubmed data. Therefore, using MCMC probit model in topic modeling application will be impractical and inconceivable due to its computational inefficiency. Nonetheless, a recent work on diagonal orthant probit model [5] substantially improved the sampling efficiency while maintaining the predictive performance, which motivated us to build an alternative correlated topic modeling with probit normal topic distribution. On the other hand, probit models inherently capture a better dependency structure between topics and co-occurrence of words within a topic as it doesn’t assume the IIA (independence of irrelevant alternatives) restriction of logistic models.
The rest of this paper is organized as follows: in Section 2, we present a conventional formulation of topic modeling along with our general notation and the correlated topic models extension. Section 3 introduces our adaptation of the diagonal orthant probit model to topic discovery in the presence correlations among topics, along with the corresponding auxiliary variable sampling scheme for updating the probit model parameters and the remainder of all the posterior distributions of the parameters of the model. Unlike with the logistic normal formulation where the non-conjugacy leads to the need for sophisticated sampling scheme, in this section we clearly reveal the simplicity of our proposed method resulting from the natural conjugacy inherent in the auxiliary formulation of the updating of the parameters. We also show compelling computational demonstrations of the efficiency of the diagonal orthant approach compared to the traditional multinomial probit for on both the auxiliary variable sampling and the estimation of the topic distribution. Section 4 presents the performance of our proposed approach on the Associated Press data set, featuring the intuitively appealing topics discovered, along with the correlation structure among topics and the loglikelihood as a function of topical space dimension. Section 5 deals with our conclusion, discussion and elements of our future work.
2. General Aspects of Topic Models
In a given corpus, one could imagine that each document deals with one or more topics. For instance, one of the collection considered in this paper is provided by the Associated Press and covers topics as varied as aviation, education, weather, broadcasting, air force, navy, national security, international treaties, investing, interna- tional trade, war, courts, entertainment industry, politics, and etc. From a statistical perspective, a topic is often modeled as a probability distribution over words, and as a result a given document is treated as a mixture of probabilistic topics [1] . We consider a setting where we have a total of 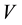 unique words in the reference vocabulary and
unique words in the reference vocabulary and 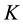 topics underlying the
topics underlying the 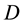 documents provided. Let
documents provided. Let 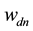 denote the n-th word in the d-th document, and let
denote the n-th word in the d-th document, and let 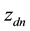 refer to the label of the topic assigned to the
refer to the label of the topic assigned to the 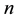 -th word of that
-th word of that 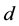 -th document. Then the probability of
-th document. Then the probability of 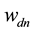 is given by
is given by
 (1)
(1)
where 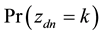 is the probability that the n-th word in the d-th document is assigned to topic
is the probability that the n-th word in the d-th document is assigned to topic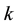 . This quantity plays an important role in the analysis of correlated topic models. In the seminal article on correlated topic models [2] ,
. This quantity plays an important role in the analysis of correlated topic models. In the seminal article on correlated topic models [2] ,  is modeled for each document
is modeled for each document 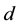 as a function of a K-dimensional vector
as a function of a K-dimensional vector 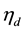
of parameters. Specifically, the logistic-normal defines  where the last element
where the last element 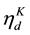 is typically set to zero for identifiability and assumes with
is typically set to zero for identifiability and assumes with ![]() with
with
![]()
Also, ![]() and
and![]() , and
, and![]() . With all these model components defined, the estimation task in correlated topic modeling from a Bayesian perspective can be summarized in the following posterior
. With all these model components defined, the estimation task in correlated topic modeling from a Bayesian perspective can be summarized in the following posterior
![]() (2)
(2)
where ![]() is defined using the Gamma function
is defined using the Gamma function ![]() so for a
so for a ![]() -dimension vector
-dimension vector![]() ,
,
![]()
(3) provides the ingredients for estimating the parameter vectors ![]() that help capture the correlations among topics, and the matrix
that help capture the correlations among topics, and the matrix ![]() that contains the topical assignments. Under the logistic normal model, sampling from the full posterior of
that contains the topical assignments. Under the logistic normal model, sampling from the full posterior of ![]() derived from the joint posterior in (3) requires the use of sophisticated sampling schemes like the one used in [4] . Although these authors managed to achieve great performances on large corpuses of documents, we thought it useful to contribute to correlated topic modeling by way of the multinomial probit. Clearly, as indicated earlier, most authors concentrated on logistic-normal even despite non-conjugacy, and the lack of probit topic modeling can be easily attributed to the inefficiency of the corresponding sampling scheme. In the most raw formulation of the multinomial probit that intends to capture the full extend of all the correlations among the topics, the topic assignment probability is defined by (3).
derived from the joint posterior in (3) requires the use of sophisticated sampling schemes like the one used in [4] . Although these authors managed to achieve great performances on large corpuses of documents, we thought it useful to contribute to correlated topic modeling by way of the multinomial probit. Clearly, as indicated earlier, most authors concentrated on logistic-normal even despite non-conjugacy, and the lack of probit topic modeling can be easily attributed to the inefficiency of the corresponding sampling scheme. In the most raw formulation of the multinomial probit that intends to capture the full extend of all the correlations among the topics, the topic assignment probability is defined by (3).
![]() (3)
(3)
The practical evaluation of (3) involves a complicated high dimensional integral which is typically computationally intractable when the number of categories is greater than 4. A relaxed version of (3), one that still captures more correlation than the logit and that is also very commonly used in practice, defines ![]() as
as
![]() (4)
(4)
where ![]() is the standard normal density, and
is the standard normal density, and ![]() is the standard normal dis-
is the standard normal dis-
tribution function. Despite this relaxation, the multinomial probit in this formulation still has major drawbacks namely: 1) Even when one is given the vector![]() , the calculation of
, the calculation of ![]() remains computationally prohibitive even for moderate values of
remains computationally prohibitive even for moderate values of![]() . In practice, one may consider using a monte carlo approximation to that integral in (4). However, such an approach in the context of a large corpus with many underlying latent topics renders the probit formulation almost unusable. 2) As far as the estimation of
. In practice, one may consider using a monte carlo approximation to that integral in (4). However, such an approach in the context of a large corpus with many underlying latent topics renders the probit formulation almost unusable. 2) As far as the estimation of ![]() is concerned, a natural approach to sampling from the posterior of
is concerned, a natural approach to sampling from the posterior of ![]() in this context would be to use the Metropolis-Hastings updating scheme, since the full posterior in this case is not available. Unfortunately, the Metropolis in this case is excruciatingly slow with poor mixing rates and high sensitivity to the proposal distribution. It turns out that an apparently appealing solution in this case could come from the auxiliary variable formulation as described in [6] . Unfortunately, even this promising formulation fails catastrophically for moderate values
in this context would be to use the Metropolis-Hastings updating scheme, since the full posterior in this case is not available. Unfortunately, the Metropolis in this case is excruciatingly slow with poor mixing rates and high sensitivity to the proposal distribution. It turns out that an apparently appealing solution in this case could come from the auxiliary variable formulation as described in [6] . Unfortunately, even this promising formulation fails catastrophically for moderate values ![]() as we will demonstrate in the subsequent section, due to the high dependency structure between auxiliary variables and parameters. Essentially, the need for Metropolis is avoided by defining an auxiliary vector
as we will demonstrate in the subsequent section, due to the high dependency structure between auxiliary variables and parameters. Essentially, the need for Metropolis is avoided by defining an auxiliary vector ![]() of dimension
of dimension![]() . For
. For![]() , we consider the vector
, we consider the vector ![]() containing the current topic allocation and we repeatedly sample
containing the current topic allocation and we repeatedly sample ![]() from a
from a ![]() -dimensional multivariate Gaussian until the component of
-dimensional multivariate Gaussian until the component of ![]() that corresponds to the non-zero index in
that corresponds to the non-zero index in ![]() is the largest of all the components of
is the largest of all the components of![]() , i.e.
, i.e.
![]() (5)
(5)
The condition in (5) typically fails to be fulfilled even when ![]() is moderately large. In fact, we demonstrate later that in some cases, it becomes impossible to find a vector
is moderately large. In fact, we demonstrate later that in some cases, it becomes impossible to find a vector ![]() satisfying that condition. Besides, the dependency of
satisfying that condition. Besides, the dependency of ![]() on the current value of
on the current value of ![]() further complicates the sampling scheme especially in the case of large topical space. In the next section, we remedy these inefficiencies by proposing and developing our adaptation of the diagonal orthant multinomial probit.
further complicates the sampling scheme especially in the case of large topical space. In the next section, we remedy these inefficiencies by proposing and developing our adaptation of the diagonal orthant multinomial probit.
3. Diagonal Orthant Probit for Correlated Topic Models
In a recent work, [5] developed the diagonal orthant probit approach to multicategorical classification. Their approach circumvents the bottlenecks mentioned earlier and substantially improves the sampling efficiency while maintaining the predictive performance. Essentially, the diagonal orthant probit approach successfully makes the most of the benefits of binary classification, thereby substantially reducing the high dependency that made the condition (5) computationally unattainable. Indeed, with the diagonal orthant multinomial model, we achieved three main benefits
・ A more tractable and easily computatble definition of topic distribution ![]()
・ A clear and very straightforward and adaptable auxiliary variable sampling scheme
・ Thecapacity to handle a very large number of topics due to the efficiency and low dependency.
Under the diagonal orthant probit model, we have
![]() (6)
(6)
The generative process of our probit normal topic models is essentially identical to logistic topic models except that the topic distribution for each document now is obtained by a probit transformation of a multivariate Gaussian variable (6). As such, the generating process of a document of length ![]() is as follows:
is as follows:
1) Draw ![]() and transform
and transform ![]() into topic distribution
into topic distribution ![]() where each element of
where each element of ![]() is computed as follows:
is computed as follows:
![]() (7)
(7)
2) For each word position ![]()
a) Draw a topic assignment ![]()
b) Draw a word ![]()
Where ![]() represents the cumulative distribution of the standard normal. We specify a Gaussian prior for
represents the cumulative distribution of the standard normal. We specify a Gaussian prior for![]() , namely
, namely![]() . Throughout this paper, we’ll use
. Throughout this paper, we’ll use ![]() to denote the
to denote the ![]() -dimensional multivariate Gaussian density function,
-dimensional multivariate Gaussian density function,
![]()
To complete the Bayesian analysis of our probit normal topic model, we need to sample from the joint posterior
![]() (8)
(8)
As noted earlier, the second benefit of the diagonal orthant probit model lies in its clear, simple, straightforward yet powerful auxiliary variable sampling scheme. We take advantage of that diagonal orthant property when dealing with the full posterior for ![]() given by
given by
![]() (9)
(9)
While sampling directly from (9) is impractical, defining a collection of auxiliary variables ![]() allows a scheme that samples from the joint posterior
allows a scheme that samples from the joint posterior ![]() using the following:
using the following:
For each document![]() , the matrix
, the matrix ![]() contains all the values of the auxiliary variables,
contains all the values of the auxiliary variables,
![]()
Each row ![]() of
of ![]() has
has ![]() components, and the diagonal orthant updates them
components, and the diagonal orthant updates them
readily using the following straightforward sampling scheme: Let ![]() be the current topic allocation for the nth word.
be the current topic allocation for the nth word.
・ For the component of ![]() whose index corresponds to the label of current topic assignment of word
whose index corresponds to the label of current topic assignment of word ![]() sample from a truncated normal distribution with variance 1 restricted to positive outcomes
sample from a truncated normal distribution with variance 1 restricted to positive outcomes
![]()
・ For all components of ![]() whose indices do correspond to the label of current topic assignment of word
whose indices do correspond to the label of current topic assignment of word ![]() sample from a truncated normal distribution with variance 1 restricted to negative outcomes
sample from a truncated normal distribution with variance 1 restricted to negative outcomes
![]()
Once the matrix ![]() is obtained, the sampling scheme updates the parameter vector
is obtained, the sampling scheme updates the parameter vector ![]() by conveniently drawing
by conveniently drawing
![]()
where
![]()
with ![]() and
and ![]() representing the row-wise vectorization of the matrix
representing the row-wise vectorization of the matrix![]() . Adopting the fully Bayesian treatment of our probit normal correlated topic model, we add an extra layer to the hierarchy in order to capture the variation in the mean vector and the variance-covariance matrix of the parameter vector
. Adopting the fully Bayesian treatment of our probit normal correlated topic model, we add an extra layer to the hierarchy in order to capture the variation in the mean vector and the variance-covariance matrix of the parameter vector![]() . Taking advantage of conjugacy, we specify a normal-Inverse-Wishart prior for
. Taking advantage of conjugacy, we specify a normal-Inverse-Wishart prior for![]() , namely,
, namely,
![]()
meaning that ![]() and
and![]() . The corresponding posterior is normal-inverse-Wishart, so that we can write
. The corresponding posterior is normal-inverse-Wishart, so that we can write
![]()
where![]() ,
, ![]() ,
, ![]() , and
, and
![]()
where
![]()
As far as sampling from the full posterior distribution of ![]() is concerned, we use the expression
is concerned, we use the expression
![]()
where the use of ![]() is used to indicate that the n-th word is not included in the topic or document under consideration.
is used to indicate that the n-th word is not included in the topic or document under consideration.
4. Computational Results on the Associated Press Data
In this section, we used a famous Associated Press data set from [7] in R to uncover the word topic distribution, the correlation structure between various topics as well as selecting optimal models. The Associated Press corpus consists of 2244 documents and 10,473 words. After preprocessing the corpus by picking frequent and common terms, we reduced the size of the words from 10,473 to 2643 for efficient sampling.
In our first experimentation, we built a correlated topic modeling structure based on the traditional multinomial probit and then tested the computational speed for key sampling tasks. The high posterior dependency structure between auxiliary variables and parameters make multinormal probit essentially unscalable for situations where it is impossible for the sampler to yield a random variate of the auxiliary variable corresponding the current topic allocation label that is also the maximum (5). For a random initialization of topic assignment, the sampling of auxiliary variable cannot even complete one single iteration. In the case of good initialization of topical prior ![]() which leads to smooth sampling of auxiliary variables, the computational efficiency is still undesirable and we observed that for larger topical space such as K = 40, the auxiliary variable stumbled again after some amount of iterations, indicating even good initialization will not ease the troublesome dependency relationship between the auxiliary variables and parameters in larger topical space. Unlike with the traditional probit model for which the computation of
which leads to smooth sampling of auxiliary variables, the computational efficiency is still undesirable and we observed that for larger topical space such as K = 40, the auxiliary variable stumbled again after some amount of iterations, indicating even good initialization will not ease the troublesome dependency relationship between the auxiliary variables and parameters in larger topical space. Unlike with the traditional probit model for which the computation of ![]() is virtually impractical for large
is virtually impractical for large![]() , the diagonal orthant approach makes this computation substantially faster ever for large
, the diagonal orthant approach makes this computation substantially faster ever for large![]() . The comparison of the computational speed of two essential sampling tasks between the multinomial probit model and digonal orthant probit model are shown as below in Table 1.
. The comparison of the computational speed of two essential sampling tasks between the multinomial probit model and digonal orthant probit model are shown as below in Table 1.
![]()
Table 1. All the numbers in this table represent the processing time (in se- conds), and are computed in Ron PC using a parallel algorithm acting on 4 CPU cores. NA here represents situations where it is impossible for the sampler to yield a random variate of the auxiliary variable corresponding the current topic allocation label that is also the maximum.
In addition to the drastic improvement of the overall sampling efficiency, we noticed that the computational complexity for sampling the auxiliary variable and topic distribution is close to O(1) and O(K) respectively, suggesting that probit normal topic model now becomes an attainable and feasible tool of the traditional correlated topic model.
Central to topic modeling is the need to determine for a given corpus the optimal number of latent topics. As it is the case for most latent variable models, this task can be formidable at times, and there is no consensus among machine learning researchers as to which of the existing methods is the best. Figure 1 shows the loglikelihood as a function of the number of topics discovered in the model. Apart from the loglikelihood, many other techniques are commonly used such as perplexity, harmonic mean method and so on.
As we see, the optimal number of topics in this case is 30. In Table 2, we show a subset of the 30 topics uncovered where each topic is represented by the 10 most frequent words. It can be seen that our probit normal topic model is able to capture the co-occurrence of words within topics successfully. In Figure 2, we also show the correlation structure between various topics which is the essential purpose of employing the correlated topic model. Evidently, the correlation captured intuitively reflect the natural relationship between similar topics.
5. Conclusion and Discussion
In the context of topic modeling where many other researchers seem to have avoided it. By adapting the diagonal orthant probit model, we proposed a probit alternative to the logit approach to the topic modeling. Compared to the multinomial probit model we constructed, our topic discovery scheme using diagonal orthant probit model enjoyed several desirable properties; First,we gained the efficiency in computing the topic distribution![]() ; Second, we achieved a clear and very straightforward and adaptable auxiliary variable sampling scheme that substantially reduced the strength of the dependence structure between auxiliary variables and model parameters, responsible for absorbing state in the Markov chain; Thirdly, as a consequence of good mixing, our approach made the probit model a viable and competitive alternatives to its logistic counterpart. In addition to all these benefits, our proposed method offers a straightforward and inherent conjugacy, which helps avoid those complicated sampling schemes employed in the logistics normal probit model.
; Second, we achieved a clear and very straightforward and adaptable auxiliary variable sampling scheme that substantially reduced the strength of the dependence structure between auxiliary variables and model parameters, responsible for absorbing state in the Markov chain; Thirdly, as a consequence of good mixing, our approach made the probit model a viable and competitive alternatives to its logistic counterpart. In addition to all these benefits, our proposed method offers a straightforward and inherent conjugacy, which helps avoid those complicated sampling schemes employed in the logistics normal probit model.
In the Associated Press example explored in the previous section, not only does our method produce a better likelihood than the logistic normal topic model with variational EM, but also discovers meaningful topics along with underlying correlation structure between topics. Overall, the method we developed in this paper offers another feasible alternatives in the context of correlated topic model that we hope will be further explored and extended by many other researchers.
![]()
Figure 1. Log likelihood as a function of the number of topics.
![]()
Table 2. Representation of topics discovered by our method.
Based on the promising results we have seen in this paper, the probit normal topic model opens the door for various future works. For instance, [8] proposed a multi-field correlated topic model by relaxing the assumption of using common set of topics globally among all documents, which can also be applied to the probit model to enrich the comprehensiveness of structural relationships between topics. Another potential direction would be to
![]()
Figure 2. Graphical representation of the correlation among topics.
enhance the scalability of the model. Currently we used a simple distributed algorithm proposed by [9] and [10] for efficient Gibbs sampling. The architecture for topic models presented by [11] can be further utilized to reduce the computational complexity substantially while delivering comparable performance. Furthermore, a novel sampling method involving the Gibbs Max-Margin Topic [12] will further improve the computational efficiency.
Acknowledgements
We want to express our sincere gratitude to our reviewer for comprehensive and constructive advice. We also wish to express our heartfelt gratitude and infinite thanks to Our Lady of Perpetual Help for Her ever-present support and guidance, especially for the uninterrupted flow of inspiration received through Her most powerful intercession.