Dynamics of Drainage of Power-Law Liquid into a Deformable Porous Material ()
1. Introduction
In this study we develop a model for the drainage of a power law liquid into deformable porous materials. The motivation of this work is connected to many scientific fields, such as oil recovery, inkjet printing, textile engineering, soil consolidation, reservoir engineering and biomechanics. The movement of fluid through the porous materials swells the porous material which in turn affects the flow of fluid. This alteration in fluid flow and deformation of the porous material identifies the complexity and importance of these flows. Interestingly enough, most of the fluids involved in these processes are not Newtonian in nature and hence should be incorporated in the complex dynamics of deformation. To accommodate this need, we present a coupled model for deformation of porous material and drainage of power law fluids.
An overview of literature shows that the deformation of porous materials couple with fluid flow goes back to Terzaghi [1] . This idea was later extended by Biot [2] [3] to study soil consolidation. Later on, mixture theory [4] [5] was introduced to enhance the understanding of material deformation causes by fluid imbibition. Some of the biological applications that use the mixture theories include articular cartilage [6] - [12] , arterial tissue [13] - [16] and skin [17] . Note that most of the fluids involved in the above referenced biological studies possess non- Newtonian properties and therefore, non-Newtonian properties must be incorporated with the mixture theory in future studies.
Most industrial applications (e.g. composite materials, paper and inkjet printing, and dyeing of colored fabrics) involve fluids that are non-Newtonian. In an effort to address this behavior, Sommer and Mortensen [18] studied a forced unidirectional infiltration of deformable porous materials. They considered a constant pressure driven flow in an initially dry sponge like material and an agreement between theory and experiment was reported. A similar model of an infiltration of an incompressible liquid into an initially dry porous material was developed by Preziosi et al. [19] , where they allowed the porous material to deform and relax. Another study that uses mixture theory to model the imbibition of a liquid droplet on a deformable substrate in a one dimensional setting was presented by Anderson [20] . In the absence of gravity effects, the imbibition causes swelling, swelling relaxation and shrinking of a porous material.
The history of capillary rise into porous media goes back to the classical model first presented by Washburn [21] . This model shows that the amount of liquid imbibed into a porous material is proportional to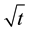
. To validate the Washburn model, Zhmud et al. [22] and Lago and Araujo [23] presented an experimental and theoretical model of capillary rise into porous materials. Their results are consistent with the Washburn model for initial times and deviate from this trend for long times. Following these studies, Siddique et al. [24] presented an analog of the Washburn model of capillary rise. Mixture theory has been used to take into account the deformation of porous materials.
The non-Newtonian modeling along with the mixture theory was studied by Siddique and Anderson [25] . In particular, they studied the capillary rise of a power law fluid into a deformable porous material, where they assumed imbibition occurring from an infinite bath of power law fluid. When gravity effects are present, both liquid and solid interface positions reach equilibrium heights depending upon the power law index n. This study mimics only one particular aspect of capillary rise; however the need is to extend the current power law model along with mixture theory to explore many other physical settings. In this study we explore the drainage of a finite amount of liquid into deformable porous materials in the presence and absence of gravity effects.
There are many types of non-Newtonian fluid models, e.g. Herschel-Bulkley fluid, power law and differential fluid type, etc. These fluid models have been widely used in a variety of settings to analyze various physical aspects. Most relevant ones are Christopher and Middleman [26] , Sadowski [27] and Hayes et al. [28] . These studies explained some of the important aspects of porous medium flow based on power law model but there are still important phenomena to explain and clarify. The current study is an effort to model the power law fluid with mixture theory (for details see [25] ).
In this paper, we study the drainage of a power law fluid into deformable porous material. The initial height 
of fluid is modeled via an Equation. Our experiments of drainage of silicon oil with low and high viscosity into deformable porous material encouraged us to present a mathematical model that can be used to predict the similar dynamics of drainage. We do this by following Siddique et al. [24] [25] . We hope that our preliminary efforts in this regard may lead to further investigate the additional features of flows in complex porous media.
2. Experiment
A sample of polyurethane foam (pore size ca. 50 - 150 mm (Figure 1)) was cut into a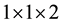 
cm piece. The foam was then inserted into a 1 cm2 plastic cuvette with a hole drilled in the bottom to allow for drainage. The foam fit just snuggly in the cuvette so that liquid could not flow around the foam, but little compression of the
![]()
Figure 1. Optical micrograph of a cross-section of the polyurethane foam.
foam occurred which would alter the drainage of the liquid (Figure 2). Two samples of silicon oil (polydimethylsiloxane) were used as the drainage fluid: a low viscosity sample (10 cPs) and a high viscosity sample (1000 cPs). Since these non-Newtonian silicon oils have identical chemical structure, their molecular interaction with the foam should also be identical; however, they have different molar masses, which is manifested in their differences in viscosity. Only these differences in viscosity should affect their drainage through the foam. A single grain of solid iodine was dissolved in both silicon oils to provide contrast with the foam and aid in the determination of the movement of the oils through the foam. It is not expected that the presence of the iodine will alter the drainage of the oils. 1 mL of the dyed silicon oil was injected into the top of the cuvette and it began to drain into the foam. A digital camera operating at 30 frames per second and a resolution of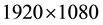 
pixels was used to record the flow of the silicon oils through the foam. Using the images produced by the camera, the position (in pixels) of the oil above the foam, 
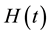, the foam interface position, 
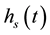, and the liquid interface, 
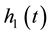, were determined as a function of time (Figure 2). The distance in pixels was converted to distance in mm using the length of the cuvette (1 cm) as a scale. The experiment was concluded when the level of the silicon above the foam reached the level of the foam.
Experimental Results
Figure 2 shows a representative drainage experiment using the high viscosity silicon oil as the fluid. The beginning point (0 s in Figure 2) was chosen as the image where all of the 1 mL volume of silicon oil had been added to the cuvette. As the experiment continued, the height of the liquid above the foam,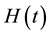 
, and the liquid interface position, 
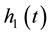, both dropped as the oil absorbed into the foam (10 s and 30 s in Figure 2). This experiment was terminated when all of the silicon oil had penetrated into the foam (when 
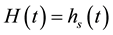at ca. 100 s). The positions of each of the three interfaces are plotted as a function of time in Figure 3 for both the low and high viscosity silicon oils. It took approximately 4 s for the low viscosity oil to completely drain into the foam while the higher viscosity oil took significantly longer at 100 s.
It should be noted that no measurable expansion of the foam was observed (i.e.,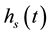 
was constant) for these foams when imbibed with either silicon oil. This is in contrast to drainage experiments where low molar
![]()
Figure 2. Representative photographs showing the drainage of the high viscosity silicon oil into the polyurethane foam at different time intervals. The liquid height above the foam, the foam height, and the liquid interface are labeled (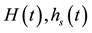
, and
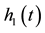, respectively).
mass alcohols such as ethanol were used. While ethanol has similar rapid drainage characteristics to the low viscosity silicon oil, it differed in that it also caused a significant expansion of the foam. Ethanol is a polar liquid that can interact strongly with the polyurethane foam causing expansion. In contrast, the silicon oil is essentially nonpolar and will not interact strongly with the foam resulting in little expansion. Clearly the expansion of the foam is very dependent on the nature of the intermolecular interactions between the foam and the liquid and will be examined in future research efforts.
Figure 3 shows the dynamics behavior of the low and high viscosity silicon oils into the polyurethane foam. Here the curves are shown in dimensional form. The dashed curves shows the initial height as a function of time![]()
, the solid line shows the deformation of foam as function of time ![]()
and drainage of liquid as a function of time![]()
.
3. Mathematical Modeling
The basic geometrical description for our problem is shown in Figure 4. We consider a finite amount of a non- Newtonian liquid with an initial height defined as ![]()
in contact with a deformable porous material at time![]()
. In the figure this initial contact position between the liquid and the deformable porous material is specified by![]()
. We assume the pressure at the positions ![]()
is atmospheric pressure. Later, the height of the liquid will be represented by the Equation for![]()
. After time![]()
, the non-Newtonian liquid starts to imbibe into the deformable porous material which in turn deforms the porous material and forms two interfaces: the upper interface![]()
, and lower interface![]()
, as can be seen from Figure 4. In order to define the dimensionless system of equations, we use the following set of scaling parameters
![]()
The above dimensionless quantities suggest the following time and length scales after balancing the terms in
both momentum equations ![]()
and ![]()
Note that this choice of time scale depends on power-
law index ![]()
We will present the details on how to make this choice of time scale independent of power law index ![]()
for numerical simulation in the result section. In the above defined set of scaling parameters we use ![]()
and ![]()
are representative scales for solid stress and the permeability respectively. We follow Siddique and Anderson [25] where they defined the permeability ![]()
in terms of the permeability of bed particles of diameter ![]()
and solid volume fraction ![]()
(see Hayes et al. [28] and references therein for details)
![]()
(1)
and ![]()
for the power law fluid is given by
![]()
(2)
where
![]()
Note, setting ![]()
in ![]()
relation and Equation (2) yields ![]()
that represents the Newtonian viscosity. The resulting set of Equations describing the one-dimensional drainage of non-Newtonian liquid (e.g. power law) into deformable porous material after dropping the primes is
![]()
(3)
![]()
(4)
![]()
(5)
![]()
(6)
where ![]()
and stress is a function of solid volume fraction ![]()
Following Anderson 2005, we assume ![]()
This choice is suitable for one dimensional deformation and needs to be generalized to take into account effects such as shear deformation in a higher dimension. It is worthwhile mentioning that subscript ![]()
and ![]()
represent the derivative with respect to corresponding variables.
Equations (3) and (4) represent mass balances and Equations (5) and (6) are momentum balances for the solid and liquid phases (see [25] ). The set of parameters in these Equations can be divided into two categories, first set of parameters inside the wet material regions such as the solid volume fraction![]()
, the liquid ![]()
and solid ![]()
component of velocities, the liquid pressure ![]()
the solid stress![]()
, and the permeability of porous material and second set represents liquid ![]()
and solid ![]()
boundary positions.
We follow the same procedure as was followed in Anderson (2005), Siddique et al. [24] , and Siddique and Anderson [25] to obtain the partial differential equation for the solid volume fraction ![]()
in the wet sponge region ![]()
![]()
(7)
The appropriate boundary conditions for the solid volume fraction are
![]()
(8)
![]()
(9)
In the derivation of boundary condition (8), we integrate Equation (6) after substituting ![]()
and applying the pressure boundary conditions given below in (12) and (15). The liquid height Equation is derived using a conservation of liquid argument (see Siddique et al. [24] )
![]()
(10)
where ![]()
represents the initial height of the non-Newtonian liquid before it starts to drain into deformable porous material.
The boundary conditions at the liquid-wet material interface ![]()
are
![]()
(11)
![]()
(12)
![]()
(13)
where ![]()
is the dimensionless constant atmospheric pressure. Here, Equations (11)-(13) represent the kinematic, hydrostatic, and zero stress conditions respectively. While modeling hydrostatic boundary condition (12) we have neglected the inertial effects.
The kinematic and pressure boundary conditions at wet-material-dry material interface ![]()
are
![]()
(14)
![]()
(15)
where ![]()
represents the dimensionless constant capillary pressure.
Boundary conditions (11) and (14) transform to ordinary differential Equations for the solid and liquid interfaces
![]()
(16)
![]()
(17)
where ![]()
![]()
(18)
If we take ![]()
in Equation (7) we recover Equation (9) of Siddique et al. [24] in dimensionless form and if we take ![]()
and ![]()
in (7) we recover Equation (20) of Anderson [20] in dimensionless form and Equation (44) of Prezoisi et al. [5] . The steady state solution of the above system is the same as for the Newtonian case (see Siddique et al. [24] ). Below we will summarize the solution procedure in the absence of gravity and in the presence of gravity effects.
4. Gravity Independent Solution
In the absence of gravity effects, Equation (7) admits the solution in terms of a similarity variable
![]()
that yields the following ordinary differential Equation
![]()
(19)
subject to the boundary conditions ![]()
and![]()
, where ![]()
The boundary condition, ![]()
is obtained by substituting ![]()
in Equation (6), integrating, and using boundary con- ditions (12) and (15) in the absence of gravity. Note that ![]()
and ![]()
represents the interface positions in terms of the similarity variables given below. Similarly, introducing ![]()
and ![]()
yields this following relations for ![]()
and ![]()
![]()
(20)
![]()
(21)
The non-linear ODE (19) along with the non-linear Equations (20) and (21) is solved numerically. The ODE and non-linear Equations are discretized using finite difference and midpoint rule yielding a system of non-linear Equations. This coupled system of non-linear Equations is solved numerically. We will present the solution of zero gravity case in the results section. It is worthwhile highlighting that this numerically computed zero gravity solution will be used as an initial condition for non-zero gravity case which we will discuss in the section below.
5. Non-Zero Gravity Solution
In the presence of gravity effects, we will first transform the moving domain problem given by (7) along with (16) and (17) to fixed domain using the following transformation
![]()
(22)
This helps transforming the moving domain problem ![]()
to a fixed domain problem![]()
. We use ![]()
and ![]()
initial conditions for solid and liquid interface positions respectively. We use method of lines along with boundary conditions given in (8) and (9). Again, we use the zero gravity solution as initial conditions for the non-zero gravity case. We approximate the spatial derivatives using second order ac- curate finite difference and mid-point discretizations. This reduces the system of partial differential Equations (PDEs) to system of ordinary differential Equations (ODEs) in time which is solved using Matlab’s solver ode23s. We start our numerical integration for ![]()
where ![]()
is a numerical small value.
6. Results
Our results are based on a specific set of test fluids for which power-law index ![]()
and consistency index ![]()
values are available (see Missirlis et al. [29] ). The calculation of the ![]()
values is based on the assumption that the capillary pressure ![]()
where ![]()
is the surface tension assumed to be same and non-New- tonian case and ![]()
is the wetting angle, that we also assumed to be![]()
. We introduce the Newtonian time scale ![]()
in such a way that computed simulation results are independent of the power law index ![]()
Note that the time scales are related through capillary pressure ![]()
that depends on particle diameter ![]()
When capillary pressure increases the drainage of fluid increases. Although we do not explore the dependence on ![]()
here, increasing ![]()
means increasing friction force. In other words, ![]()
is directly proportional to the drainage process.
In the beginning of the process, a finite amount of liquid is supplied, whose height is shown by ![]()
in Figure 5. It is important to note that when gravity effects are not present, the solution is independent of ![]()
and both interface positions ![]()
and ![]()
admits similarity solution until the entire fluid is drained into the deformable porous material (i.e.,![]()
). Figure 5 summarizes the drainage comparison between the Newtonian and different power law fluids. Each of these curves corresponds to set of parameters ![]()
used in sponge experiment in Siddique et al. [24] along with power law consistency index ![]()
and the power law index ![]()
values from Missirlis et al. [29] . However it is important to note that equilibrium heights ![]()
and ![]()
attained depend on the values of ![]()
and![]()
. The bottom right of Figure 5 shows power law
index ![]()
as a function of ![]()
As ![]()
decrease the drainage time increases. We denote this drainage time as![]()
. It is interesting to note that both the Newtonian and non-Newtonian fluids follow the similarity behavior but as ![]()
decreases, ![]()
increases which means decreasing the ![]()
values slows down the dynamics. Figure 6 shows the drainage of liquid into a deformable porous material in the presence of gravity effects. The time scales used in Figure 6 allow us to present a direct comparison for different values of ![]()
Similar to the Newtonian case, a finite amount of liquid is supplied, shown by ![]()
in Figure 6. For this case, both curves ![]()
and ![]()
follow similarity solution for very short time and then depart from this behavior until the fluid is entirely drained into porous material. The drainage time for the nonzero gravity case is faster than the zero gravity case.
In order to connect our theoretical predictions with experiments, we performed drainage of silicon oil of two different viscosities with identical chemical structure into deformable sponge like materials. Our experimental predictions show a similar trend for drainage and deformation of deformable porous materials. The drainage of water into deformable porous material follow approximately ![]()
which is expected for the case of Newtonian fluids. Our experimental curves shows a modified power law of ![]()
and ![]()
for two different set of silicon oils which suggests ![]()
and ![]()
respectively. Although we are unable to present a direct qualitative comparison between theory and experiments due to limited access to experimental facilities but our finding shows that any fluid having different properties than water require different power law behavior. We hope our findings with these preliminary comparison will encourage further experimental investigation leading to capture the realistic drainage phenomena.
7. Discussion
In this present work we have presented a basic model for predicting the drainage of a power law liquid into a deformable porous material. More specifically, we transform the capillary rise theory developed for power law liquids into deformable porous materials [24] to the drainage setting by specifying liquid height [25] via an equation based on conservation of liquid argument. In addition to theoretical predictions, this work includes a set of experiments showing the similar behavior as shown in our numerically simulations. In this study we use the mixture theory [15] [16] [18] - [20] [24] [25] to model the problem of drainage of power law liquid into deformable porous material.
In the absence of gravity effects, the deformation of the porous material and the penetration of liquid follows
a different power law behavior ![]()
compared to the Newtonian case. Our findings show that the dynamics for
both ![]()
and ![]()
follow different dynamics compared to the Newtonian case. We were able to compute the drainage time for different fluids. These findings are consistent with our experimental findings. When gravity effects are present in our model, the drainage of power law liquid depends on ![]()
Note that both curves, ![]()
and![]()
, follow similarity solution initially and then depart from this trend depending upon their power law consistency index ![]()
and power law index ![]()
In short, the dynamics for fluid with different properties follow different dynamics.
The present study is preliminary, but suggests some interesting possibilities in the theory of drainage of power law fluid. An interesting area to explore in future investigations would be the use of a more generalized function for solid stress ![]()
and a complicated permeability function ![]()
and for exploring the deformation in higher dimension. Alternatively, keeping a simplified functions for ![]()
and ![]()
and extending the ability to directly compare the theoretical and experimental predictions could lead to a better understanding of the basic mechanisms of drainage
Acknowledgements
The author J. I. Siddique greatly appreciate the support of Simons Foundation Grant No. 281839.