The Rise of Solitons in Sine-Gordon Field Theory: From Jacobi Amplitude to Gudermannian Function ()
1. Introduction
The sine-Gordon field theory and the associated massive Thirring model [1] are some of the best studied quantum field theories. In view of its connections to other important physical models, some of which in principle admit actual realizations in nature [2] [3] , a huge mass of important exact results have been obtained for this fascinating integrable system [4] - [7] . However, no less fascinating are the remarkable mathematical and physical properties of its soliton (or “solitary wave”) solutions which have contributed, along the last decades, to turning the physics of solitons into a very active research topic.
In this work we present a simple and yet appealing step-by-step derivation of a more general solution for the classical sine-Gordon field theory in (1 + 1)-dimensions in terms of a special kind of elliptic function, namely the Jacobi amplitude, which has the famous sine-Gordon soliton solution as a particular case. Despite the fact that the connection between solitons and Jacobi elliptic functions has already been explored in [8] , we believe that this work comes to shed more light on this interesting subject, helping to fill in a gap existing in the corres- ponding specialized literature.
2. An Alternative Pathway to Solitons in Sine-Gordon Field Theory
2.1. The Jacobi Amplitude Function
We start by considering the following theory describing a real scalar field in (1 + 1)-dimensions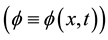 ,
,
 (1)
(1)
where the potential term is given by
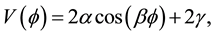 (2)
(2)
with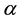 ,
, 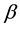 and
and 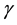 being real parameters.
being real parameters.
The above Lagrangian gives rise, through the Euler-Lagrange equation, 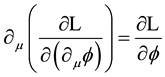 , to the following field equation
, to the following field equation
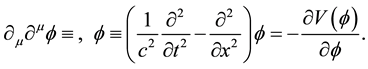 (3)
(3)
Notice that since Equation (3) is invariant under Lorentz transformations 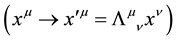 [9] , its solutions may be obtained through the solutions of the corresponding equation for the static case
[9] , its solutions may be obtained through the solutions of the corresponding equation for the static case 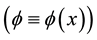 by a simple Lorentz boost, namely
by a simple Lorentz boost, namely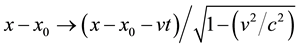 , for arbitrary
, for arbitrary 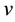
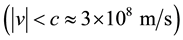 [10] [11] . Thus, in what follows, we will focus on the solutions of the equation
[10] [11] . Thus, in what follows, we will focus on the solutions of the equation
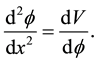 (4)
(4)
Indeed, by multiplying the above equation by 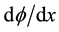 we obtain
we obtain
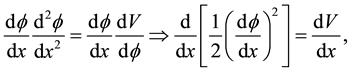 (5)
(5)
which, after an integration with respect to ![]() and some algebra, may be rewritten as
and some algebra, may be rewritten as
![]() (6)
(6)
By integrating both sides of the above equation, from ![]() to
to ![]() (
(![]() to
to![]() ), we get
), we get
![]() (7)
(7)
In order to compute the above integral, we must firstly notice that the potential, shown in Equation (2), may be rewritten as
![]() (8)
(8)
Thus, by making the change of variables![]() , defining
, defining ![]() and choosing
and choosing ![]() such that
such that![]() , we are left with
, we are left with
![]() (9)
(9)
The integral appearing in Equation (9) is called an incomplete elliptic integral of the first kind, ![]() , whereas
, whereas ![]() is called the elliptic modulus or eccentricity. The upper limit,
is called the elliptic modulus or eccentricity. The upper limit, ![]() , of this integral may be written in terms of the Jacobi amplitude (the inverse function of the incomplete elliptic integral of the first kind) as [12] [13]
, of this integral may be written in terms of the Jacobi amplitude (the inverse function of the incomplete elliptic integral of the first kind) as [12] [13]
![]() (10)
(10)
Notice that, from the above definition, we have![]() .
.
The solution of Equation (4) may be, finally, written as
![]() (11)
(11)
Hence, from the above equation, we may notice that
![]() (12)
(12)
as it should.
2.2. The Case![]() : The Gudermannian Function and the Soliton Solution of Sine-Gordon Equation
: The Gudermannian Function and the Soliton Solution of Sine-Gordon Equation
From the definition ![]() we may obviously see that when
we may obviously see that when ![]() we have
we have![]() . Hence, the solution for Equation (4) with the potential given by
. Hence, the solution for Equation (4) with the potential given by
![]() (13)
(13)
may be obtained as a special case of the solution presented in Equation (11). Indeed, since
![]()
where ![]() is called the Gudermannian function (a special function which relates the circular functions to the hyperbolic ones without using complex numbers, named after Christoph Gudermann (1798-1852)), we are left with
is called the Gudermannian function (a special function which relates the circular functions to the hyperbolic ones without using complex numbers, named after Christoph Gudermann (1798-1852)), we are left with
![]() (14)
(14)
Last but not least, we must notice that by substituting the Equation (14) into Equation (3) and making the
change (Lorentz boost)![]() , we obtain the famous sine-Gordon field equation, namely
, we obtain the famous sine-Gordon field equation, namely
![]() (15)
(15)
where ![]() is the no less famous soliton/anti-soliton solution [10] [11] , given by
is the no less famous soliton/anti-soliton solution [10] [11] , given by
![]() (16)
(16)
This result allows us to characterize the Lorentz boosted, and shifted by![]() , version of the solution in terms of the Jacobi amplitude shown in Equation (11), namely
, version of the solution in terms of the Jacobi amplitude shown in Equation (11), namely
![]() (17)
(17)
as a generalization of the sine-Gordon soliton/anti-soliton solution for![]() .
.
3. Concluding Remarks
We would like to make a few comments about the soliton solution, shown in Equation (16), and its generalized version, shown in Equation (17). Firstly, we may notice by comparing Figure 1 and Figure 2 how different are these solutions, where we would like to highlight the doubly periodic behaviour of the Jacobi amplitude solution.
Finally, let us observe that, as remarked in [10] , this soliton solution, though arising in a classical field theory, looks very much like a classical particle since its energy density is localized at a point ![]() and its total energy for a static field configuration
and its total energy for a static field configuration![]() , namely
, namely
![]() (18)
(18)
is finite, just as we should expect.
Acknowledgements
This work has been supported by University of Alberta’s Li Ka Shing Applied Virology Institute and CNPq, Conselho Nacional de Desenvolvimento Científico e Tecnológico, Brasil.