A Multi-Secret Sharing Scheme with Many Keys Based on Hermite Interpolation ()
1. Introduction
A secret sharing scheme is one of cryptographies. A secret sharing scheme was introduced by Shamir in 1979 [1] and Blakley in 1979 [2] independently. A secret sharing scheme has been studied by many scientists until today. Now, a secret sharing scheme has some important application to several areas of the information security.
The secret sharing scheme is a method to distribute shares of a secret value―we call it a key, too―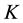 among a set of participants
among a set of participants 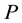 such a way that only the qualified subsets of
such a way that only the qualified subsets of  are able to reconstruct the value of
are able to reconstruct the value of 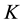 from their shares. In 1979, Shamir [1] introduced the secret sharing scheme which was based on Lagrange’s interpolation formula. This scheme is called Shamir’s threshold scheme. In 1987, Feldman [3] studied a verifiable scheme in distributing system. In 1992, Pedersen [4] applied a verifiable secret sharing scheme to Shamir’s threshold scheme.
from their shares. In 1979, Shamir [1] introduced the secret sharing scheme which was based on Lagrange’s interpolation formula. This scheme is called Shamir’s threshold scheme. In 1987, Feldman [3] studied a verifiable scheme in distributing system. In 1992, Pedersen [4] applied a verifiable secret sharing scheme to Shamir’s threshold scheme.
A secret sharing scheme has one key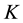 . On the other hand, a multi-secret sharing scheme has more than one keys; that is, a multi-secret sharing scheme has
. On the other hand, a multi-secret sharing scheme has more than one keys; that is, a multi-secret sharing scheme has 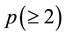 keys
keys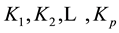 . Dealers distribute shares of keys
. Dealers distribute shares of keys
among 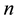 participants. Let a set of participants
participants. Let a set of participants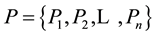 . Gathering
. Gathering 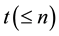 participants, keys can be reconstructed.
participants, keys can be reconstructed.
Various schemes are proposed about a multi-secret sharing scheme. In 1994, Jackson et al. [5] studied a multi-secret sharing scheme for a matroid. A multi-secret sharing scheme by utilizing a one-way function is studied by He and Dawson [6] in 1994, and by Harn [7] in 1995. A multi-secret sharing scheme by utilizing a two variables one-way function is studied by He and Dawson [8] in 1995. A multi-secret sharing scheme by utilizing a linear block code is studied by Chien et al. [9] in 2000, and by Pang and Wang [10] in 2005. A multi- secret sharing scheme based on Lagrange’s interpolation is studied by Yang et al. [11] in 2004, and by Pang and Wang [10] in 2005. Recently, Adachi [12] studies a secret sharing scheme with two keys based on Hermite interpolation.
In this paper, we give a scheme of a 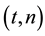 multi-secret sharing based on Hermite interpolation, in the case of
multi-secret sharing based on Hermite interpolation, in the case of![]() . Here,
. Here, ![]() is the number of keys,
is the number of keys, ![]() is the number of participants, and
is the number of participants, and ![]() is the number of gathering participants for secret reconstruction. In a
is the number of gathering participants for secret reconstruction. In a ![]() multi-secret sharing, we need to consider separately the cases where
multi-secret sharing, we need to consider separately the cases where ![]() is greater than
is greater than![]() , equal to
, equal to![]() , or less than
, or less than![]() . In this paper, we give new scheme in the case of
. In this paper, we give new scheme in the case of![]() . The goal of this paper is 1) to find system parameters, 2) to construct secret distribution, and 3) to complete secret reconstruction, for a multi-secret sharing, by utilizing Hermite interpolation.
. The goal of this paper is 1) to find system parameters, 2) to construct secret distribution, and 3) to complete secret reconstruction, for a multi-secret sharing, by utilizing Hermite interpolation.
2. Lagrange’s Interpolation and Hermite Interpolation
In this section, we describe two famous interpolation formula, that is, Lagrange’s interpolation and Hermite interpolation. In numerical analysis, Lagrange’s interpolation and Hermite interpolation is a method of interpolating data points as a polynomial function.
2.1. Lagrange’s Interpolation
Suppose that a function ![]() is defined on a closed interval
is defined on a closed interval![]() . Given
. Given ![]() data points
data points![]() , (
, (![]() ,
,![]() for
for![]() ), and values
), and values![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , we want to find an
, we want to find an ![]() dimensional polynomial
dimensional polynomial ![]() such that
such that ![]() satisfies
satisfies![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() . In other words, I want to get an approximation of
. In other words, I want to get an approximation of![]() , for any variable
, for any variable ![]() except
except ![]() data points
data points![]() , by calculating the value of an
, by calculating the value of an ![]() dimensional polynomial
dimensional polynomial![]() .
.
Here, we can get an ![]() dimensional polynomial
dimensional polynomial ![]() by the following equation.
by the following equation.
![]()
where an ![]() dimensional polynomial
dimensional polynomial ![]() satisfies
satisfies
![]()
Let![]() , we can decide an unique
, we can decide an unique ![]() dimensional polynomial
dimensional polynomial![]() . This equation is called Lagrange’s interpolation formula.
. This equation is called Lagrange’s interpolation formula.
2.2. Hermite Interpolation
Hermite interpolation is an extension of Lagrange’s interpolation. When using divided differences to calculate the Hermite polynomial of a function![]() .
.
Suppose that a function ![]() is defined on a closed interval
is defined on a closed interval![]() . Given
. Given ![]() data points
data points![]() , (
, (![]() ,
,![]() for
for![]() ), and values
), and values![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and their differential values
, and their differential values![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , we want to find a
, we want to find a ![]() dimensional polynomial
dimensional polynomial ![]() such that
such that ![]() satisfies
satisfies![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() . In other words, I want to get an approximation of
. In other words, I want to get an approximation of![]() , for any variable
, for any variable ![]() except
except ![]() data points
data points![]() , by calculating the value of a
, by calculating the value of a ![]() dimensional polynomial
dimensional polynomial![]() .
.
Here, it is known that we can get an unique ![]() dimensional polynomial
dimensional polynomial ![]() by the following equation.
by the following equation.
![]()
where two ![]() dimensional polynomial
dimensional polynomial![]() ,
, ![]() satisfy
satisfy
![]()
![]()
and
![]()
![]()
This is called Hermite interpolation.
3. A Multi-Secret Sharing Scheme Based on Lagrange’s Interpolation
In this section, we describe a multi-secret sharing scheme based on Lagrange’s interpolation, which is proposed by Yang et al. in 2004. We refer to [11] . We refer to the part of Yang’s scheme in [10] , too.
In Yang et al.’s scheme, for secret distribution, the secret are distributed in two separate cases, ![]() and
and![]() . In Yang et al.’s scheme, also, for secret reconstruction, the secret are reconstructed in two separate cases,
. In Yang et al.’s scheme, also, for secret reconstruction, the secret are reconstructed in two separate cases, ![]() and
and![]() . Since our scheme is treating in the case of
. Since our scheme is treating in the case of![]() , we describe only the case
, we describe only the case ![]() for secret distribution and for secret reconstruction, in Yang et al.’s scheme.
for secret distribution and for secret reconstruction, in Yang et al.’s scheme.
1) System parameters. Let ![]() be a two-variable one way function. Let
be a two-variable one way function. Let ![]() be a large prime and all the numbers are element in the finite field
be a large prime and all the numbers are element in the finite field![]() . The trusted dealer randomly selects
. The trusted dealer randomly selects ![]() distinct integers,
distinct integers, ![]() , as secret shadows of participants
, as secret shadows of participants![]() .
.
Here, we use ![]() to denote
to denote ![]() keys (secret values).
keys (secret values).
2) Secret distribution. In the case of![]() , the secret dealer executes the following steps:
, the secret dealer executes the following steps:
2a) Construct a ![]() -th degree polynomial
-th degree polynomial ![]()
![]() , where
, where ![]() are
are ![]() keys and
keys and ![]() are randomly chosen from
are randomly chosen from![]() .
.
2b) Randomly choose an integer ![]() and compute
and compute ![]() for
for![]() .
.
2c) Publish ![]() in any authenticated manner such as those in digital signature scheme.
in any authenticated manner such as those in digital signature scheme.
3) Secret reconstruction. In the case of![]() , at least
, at least ![]() participants pool their pseudo shadows
participants pool their pseudo shadows![]() . For example,
. For example, ![]() participants
participants ![]() pool their pseudo shadows
pool their pseudo shadows![]() . By Lagrange’s interpolation polynomial, with the knowledge of
. By Lagrange’s interpolation polynomial, with the knowledge of ![]() pairs of
pairs of![]() , the
, the ![]() -th degree polynomial
-th degree polynomial ![]() can be uniquely determined. From the obtained polynomial
can be uniquely determined. From the obtained polynomial![]() , we can easily get the
, we can easily get the ![]() keys
keys![]() .
.
4. Our Scheme: A Multi-Secret Sharing Scheme Based on Hermite Interpolation
In this section, we describe our new scheme, that is, a multi-secret sharing scheme based on Hermite interpolation in the case![]() , where
, where ![]() is the number of keys (secrets), and
is the number of keys (secrets), and ![]() is the number of necessary participants who can reconstruct keys (secrets).
is the number of necessary participants who can reconstruct keys (secrets).
In the case of![]() , the following theorem is known.
, the following theorem is known.
Theorem 1. [12] Suppose that we have two keys (secrets), ![]() is the number of participants, and
is the number of participants, and ![]()
![]() is the number of necessary participants who can reconstruct two keys (secrets). We can propose a scheme of a
is the number of necessary participants who can reconstruct two keys (secrets). We can propose a scheme of a ![]() secret sharing scheme with two keys based on Hermite interpolation.
secret sharing scheme with two keys based on Hermite interpolation.
We expand this theorem. In our scheme, at first, we prepare system parameters which we need. Secondly, we describe secret distribution. Finally, we describe secret reconstruction.
1) System parameters. Let ![]() be a two-variable one way function. Let
be a two-variable one way function. Let ![]() be a large prime and all the numbers are element in the finite field
be a large prime and all the numbers are element in the finite field![]() . The trusted dealer randomly selects
. The trusted dealer randomly selects ![]() distinct integers,
distinct integers, ![]() , as secret shadows of participants
, as secret shadows of participants![]() . The trusted dealer randomly selects an integer
. The trusted dealer randomly selects an integer![]() , calculates
, calculates![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
Here, we use ![]() to denote
to denote ![]() keys (secret values).
keys (secret values).
2) Secret distribution. In the case of![]() , the secret dealer executes the following steps:
, the secret dealer executes the following steps:
2a) He constructs a ![]() -th degree polynomial
-th degree polynomial ![]()
![]() as follows, where
as follows, where ![]() are
are ![]() keys and
keys and ![]() are randomly chosen from
are randomly chosen from![]() .
.
![]()
![]()
![]()
![]()
2b) He computes ![]() and
and ![]() for
for![]() .
.
2c) He publishes ![]() in any authenticated manner such as those in digital signature scheme.
in any authenticated manner such as those in digital signature scheme.
3) Secret reconstruction. In the case of![]() , at least
, at least ![]() participants execute the following steps:
participants execute the following steps:
3a) They pool their pseudo shadows![]() . For example,
. For example, ![]() participants
participants ![]() pool their pseudo shadows
pool their pseudo shadows![]() .
.
3b) They compute ![]() and
and ![]() for
for![]() .
.
![]()
![]()
3c) They compute ![]() and
and ![]() for
for ![]() by utilizing the solution of (3b).
by utilizing the solution of (3b).
![]()
![]()
3d) By Hermite interpolation polynomial, with the knowledge of ![]() triplets of
triplets of![]() , the
, the ![]() -th degree polynomial
-th degree polynomial ![]()
![]() can be uniquely determined as follows.
can be uniquely determined as follows.
![]()
From the obtained polynomial ![]()
![]() , we can easily get the
, we can easily get the ![]() keys
keys![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
As stated above, we obtain the following theorem.
Theorem 2. Suppose that ![]() is the number of keys (secrets),
is the number of keys (secrets), ![]() is the number of participants, and
is the number of participants, and ![]() is the number of necessary participants who can reconstruct keys (secrets). In the case
is the number of necessary participants who can reconstruct keys (secrets). In the case![]() , we can propose a scheme of a
, we can propose a scheme of a ![]() multi-secret sharing scheme with many keys based on Hermite interpolation.
multi-secret sharing scheme with many keys based on Hermite interpolation.
Corollary 1. Suppose that ![]() is the number of participants, and
is the number of participants, and ![]() is the number of necessary participants who can reconstruct keys (secrets). Theorem 2 contains a scheme of a
is the number of necessary participants who can reconstruct keys (secrets). Theorem 2 contains a scheme of a ![]() secret sharing with one key based on Lagrange’s interpolation, that is, Shamir’s threshold scheme.
secret sharing with one key based on Lagrange’s interpolation, that is, Shamir’s threshold scheme.
Proof. In the case ![]() of Theorem 2, we obtain Corollary 1.
of Theorem 2, we obtain Corollary 1.
(Q.E.D.)
Corollary 2. Theorem 2 contains Theorem 1.
Proof. In the case ![]() of Theorem 2, we obtain Corollary 2.
of Theorem 2, we obtain Corollary 2.
(Q.E.D.)
5. Computational Complexity
In this section, we compare computational complexity of our scheme which we describe in Section 4, and that of Yang et al.’s scheme which we describe in Section 3.
As regards phase 1) system parameters, the both schemes have the same amount of parameters.
As regards phase 2) secret distribution, computational complexity of our scheme is twice of that of Yang et al.’s scheme. Since, in our scheme, there are ![]() for
for![]() .
.
As regards phase 3) secret reconstruction, computational complexity of our scheme is twice of that of Yang et al.’s scheme. Since, in 3b) of our scheme, there are ![]() for
for![]() . In 3c) of our scheme, there
. In 3c) of our scheme, there
are not only ![]() but also
but also ![]() for
for![]() . In 3d) of our scheme, there are not only
. In 3d) of our scheme, there are not only ![]() but also
but also![]() .
.
Hence, computational complexity of our scheme is twice of that of Yang et al.’s scheme. This is suitable, since computational complexity of Hermite interpolation is twice of that of Lagrange’s interpolation.
6. Conclusion
We can propose a new scheme of a multi-secret sharing scheme with many keys based on Hermite interpolation. Hermite interpolation is a higher precision analysis and needs more complex computation than Lagrange’s interpolation. The merit on our scheme is that we can use many keys with fine distinctions. On the other hand, the demerit on our scheme is that its computation is complex for participants.
Acknowledgements
We thank the editor and the referee for their comments.