Some Construction Methods of A-Optimum Chemical Balance Weighing Designs ()
1. Introduction
Sir R. A. Fisher, a founder of modern concept of experimental designs gave the new ideas of designing in his first book Design of Experiment in the year 1935. Fisher’s work was continued by others; see [1] - [4] . The necessary and sufficient condition for a general block design to be variance balanced and efficiency balanced was given in the literature [5] - [8] . The concept of repeated blocks was introduced by Van Lint; see [9] . Further some potential applications of the balanced incomplete block designs with repeated blocks were presented in the literature [10] - [13] .
Another important concept which we discuss in this paper is weighing designs. The concept of weighing design was originally given by Yates and formulated as a weighing problem by Hotelling and the condition of attaining the lower bound by each of the variance of the estimated weights was given by him; see [14] [15] . In the latter developments, attention has been made in the direction of obtaining optimum weighing designs. Prominent work has been done by many researchers in this field; see [16] - [20] . In recent years, the new methods of constructing the optimum chemical balance weighing designs and a lower bound for the variance of each of the estimated weights from this chemical balance weighing design were obtained and a necessary and sufficient condition for this lower bound to be attained was proposed in the literature; see [21] - [24] . The constructions were based on the incidence matrices of balanced incomplete block designs, balanced bipartite block designs, ternary balanced block designs and group divisible designs.
Awad et al. [25] [26] gave the construction methods of obtaining optimum chemical balance weighing designs using the incidence matrices of symmetric balanced incomplete block designs and some pairwise balanced designs were also been obtained which were efficiency as well as variance balanced. In that series we now propose another new construction methods of obtaining optimum chemical balance weighing designs using the incidence matrices of symmetric balanced incomplete block designs and some more pairwise efficiency as well as variance balanced designs are proposed. Also we present the conditions under which the chemical balance weighing designs constructed by new construction methods leading to the A-optimal designs.
Let us consider 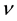 treatments arranged in
treatments arranged in 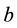 blocks, such that the
blocks, such that the 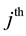 block contains
block contains 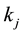 experimental units and the
experimental units and the 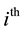 treatment appears
treatment appears 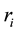 times in the entire design,
times in the entire design,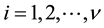 ;
;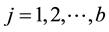 . For any block design there exist a incidence matrix
. For any block design there exist a incidence matrix  of order
of order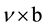 , where
, where 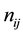 denotes the number of experiment units in the
denotes the number of experiment units in the  block getting the
block getting the 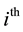 treatment. When
treatment. When 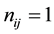 or 0
or 0 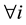 and
and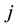 , the design is said to be binary. Otherwise it is said to be nonbinary. In this paper we consider binary block designs only. The following additional notations are used
, the design is said to be binary. Otherwise it is said to be nonbinary. In this paper we consider binary block designs only. The following additional notations are used ![]() is the column vector of block sizes,
is the column vector of block sizes, ![]() is the column vector of treatment replication,
is the column vector of treatment replication, ![]() ,
, ![]() ,
, ![]() is the total number of experimental units, with this
is the total number of experimental units, with this ![]() and
and ![]() Where
Where ![]() is the
is the ![]() vector of ones.
vector of ones.
An equi-replicate, equi-block sized, incomplete design, which is also balanced in the sense given above is called balanced incomplete block design, which is an arrangement of ![]() symbols (treatments) into
symbols (treatments) into ![]() sets (blocks) each containing
sets (blocks) each containing ![]()
![]() distinct symbols, such that any pair of distinct symbols occurs in exactly
distinct symbols, such that any pair of distinct symbols occurs in exactly ![]() sets. Then it is easy to see that each treatment occurs in
sets. Then it is easy to see that each treatment occurs in ![]()
![]() sets.
sets.![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() are called parameters of the BIBD and the parameters satisfies the relations
are called parameters of the BIBD and the parameters satisfies the relations![]() ,
, ![]() and
and ![]() (Fisher’s Inequality). A BIB design is said to be symmetric if
(Fisher’s Inequality). A BIB design is said to be symmetric if ![]() and
and![]() . In this case incidence matrix is a square matrix i.e.
. In this case incidence matrix is a square matrix i.e.![]() . In case of symmetric balanced incomplete block design any two blocks have
. In case of symmetric balanced incomplete block design any two blocks have ![]() treatments in common.
treatments in common.
Though there have been balanced designs in various senses (see [6] [27] ). We will consider a balanced design of the following type.
A block design is called variance balanced if and only if
1) It permits the estimation of all normalized treatment contrasts with the same variance (see [7] ).
2) If the information matrix for treatment effects ![]() satisfies
satisfies![]() .
.
where ![]() is the unique nonzero eigen value of the matrix
is the unique nonzero eigen value of the matrix ![]() with the multiplicity
with the multiplicity![]() ,
, ![]() is the
is the ![]() identity matrix.
identity matrix.
A block design is called efficiency balanced if
1) Every contrast of treatment effects is estimated through the design with the same efficiency factor.
2)![]() ; see [2] , and since
; see [2] , and since![]() , where
, where ![]() is the unique non zero eigen value of
is the unique non zero eigen value of ![]() with multiplicity
with multiplicity![]() . For the EB block design
. For the EB block design![]() , the information matrix
, the information matrix ![]() is given as
is given as![]() ; see [28] .
; see [28] .
A block design is said to be pairwise balanced if ![]() (a constant) for all
(a constant) for all![]() ,
, ![]() ,
, ![]() and a pairwise balanced block design is said to be binary if
and a pairwise balanced block design is said to be binary if ![]() or 1 only, for all
or 1 only, for all![]() ,
, ![]() and it has parameters
and it has parameters![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() (
(![]() , say) [in this case, when
, say) [in this case, when ![]() and
and![]() , it is a BIB design with parameters
, it is a BIB design with parameters![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ].
].
Weighing designs consists of ![]() groupings of the
groupings of the ![]() objects and suppose we want to determine the individual weights of
objects and suppose we want to determine the individual weights of ![]() objects. We can fit the results into the general linear model
objects. We can fit the results into the general linear model
![]() (1)
(1)
where ![]() is an
is an ![]() random column vector of the observed weights,
random column vector of the observed weights, ![]() is the
is the ![]() column vector repre- senting the unknown weights of objects and
column vector repre- senting the unknown weights of objects and ![]() is an
is an ![]() random column vector of errors such that
random column vector of errors such that ![]() and
and![]() .
.![]() ,
, ![]() is a
is a ![]() matrix of known quantities. The elements of matrix
matrix of known quantities. The elements of matrix ![]() take the values as
take the values as
![]()
The normal equations estimating ![]() are of the form
are of the form
![]() (2)
(2)
where ![]() is the vector of the weights estimated by the least squares method.
is the vector of the weights estimated by the least squares method.
The matrix ![]() is called the design matrix. A weighing design is said to be singular or nonsingular, depending on whether the matrix
is called the design matrix. A weighing design is said to be singular or nonsingular, depending on whether the matrix ![]() is singular or nonsingular, respectively. It is obvious that the matrix
is singular or nonsingular, respectively. It is obvious that the matrix ![]() is nonsingular if and only if the matrix
is nonsingular if and only if the matrix ![]() is of full column
is of full column![]() . Now, if
. Now, if ![]() is of full rank, that is, when
is of full rank, that is, when ![]() is nonsingular, the least squares estimate of
is nonsingular, the least squares estimate of ![]() is given by
is given by
![]() (3)
(3)
and the variance-covariance matrix of ![]() is
is
![]() (4)
(4)
When the objects are placed on two pans in a chemical balance, we shall call the weighings two pan weighing and the design is known as two pan design or chemical balance weighing design. In chemical balance weighing design, the elements of design matrix ![]() takes the values as +1 if the
takes the values as +1 if the ![]() object is placed in the left pan in the
object is placed in the left pan in the ![]() weighing,
weighing, ![]() if the
if the ![]() object is placed in the right pan in the
object is placed in the right pan in the ![]() weighing and 0 if the
weighing and 0 if the ![]() object is not weighted in the
object is not weighted in the ![]() weighing.
weighing.
Hotelling has shown that if ![]() weighing operations are to determine the weights of
weighing operations are to determine the weights of ![]() objects, the minimum attainable variance for each of the estimated weights in this case is
objects, the minimum attainable variance for each of the estimated weights in this case is ![]() and proved the theorem that each of the variance of the estimated weights attains the minimum if and only if
and proved the theorem that each of the variance of the estimated weights attains the minimum if and only if ![]() (see [14] ).
(see [14] ).
2. Variance Limit of Estimated Weights
Let ![]() be an
be an ![]() matrix of rank
matrix of rank ![]() of a chemical balance weighing design and let
of a chemical balance weighing design and let ![]() be the number of times in which
be the number of times in which ![]() object is weighed,
object is weighed, ![]() (i.e. the
(i.e. the ![]() be the number of elements equal to −1 and 1 in
be the number of elements equal to −1 and 1 in ![]() column of matrix
column of matrix![]() ). Then Ceranka et al. (see [21] ) proved the following theorem:
). Then Ceranka et al. (see [21] ) proved the following theorem:
Theorem 2.1. For any ![]() matrix
matrix![]() , of a nonsingular chemical balance weighing design, in which maximum number of elements equal to
, of a nonsingular chemical balance weighing design, in which maximum number of elements equal to ![]() and 1 in columns is equal to m, where
and 1 in columns is equal to m, where![]() .
.
Then each of the variances of the estimated weights attains the minimum if and only if
![]() (5)
(5)
Also a nonsingular chemical balance weighing design is said to be optimal for the estimating individual weights of objects if the variances of their estimators attain the lower bound given by,
![]() (6)
(6)
In SBIB design![]() ; the block intersection between any two blocks is constant i.e.
; the block intersection between any two blocks is constant i.e.![]() . Using this concept Banerjee (see [29] ) proved the following results;
. Using this concept Banerjee (see [29] ) proved the following results;
Proposition 2.2. Existence of SBIB design![]() ; implies the existence of a BIB design
; implies the existence of a BIB design ![]() with parameters
with parameters![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
Proposition 2.3. Existence of SBIB design![]() ; implies the existence of a BIB design
; implies the existence of a BIB design ![]() with parameters
with parameters![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
3. Construction of Design Matrix: Method I
In SBIB design ![]() with the parameters
with the parameters![]() ,
, ![]() ,
,![]() ; fix the
; fix the ![]() block
block![]() . Corresponding to the
. Corresponding to the ![]() fixed block, give negative sign to all the
fixed block, give negative sign to all the ![]() common treatments of remaining
common treatments of remaining ![]() blocks. Then eliminate that fixed block. Thus matrix
blocks. Then eliminate that fixed block. Thus matrix ![]() of design
of design ![]() is obtained.
is obtained.
Now doing the same procedure for all the remaining ![]() blocks, the incidence matrix
blocks, the incidence matrix ![]() of the new design
of the new design ![]() so formed is the matrix having the elements 1,
so formed is the matrix having the elements 1, ![]() and 0; given as follows
and 0; given as follows
![]() (7)
(7)
Then combining the incidence matrix ![]() of SBIB design repeated s-times with
of SBIB design repeated s-times with ![]() we get the matrix
we get the matrix ![]() of a chemical balance weighing design as
of a chemical balance weighing design as
![]() (8)
(8)
Under the present construction scheme, we have ![]() and
and![]() . Thus the each column of
. Thus the each column of ![]() will contain
will contain ![]() elements equal to 1,
elements equal to 1, ![]() elements equal to
elements equal to ![]() and
and ![]() elements equal to zero. Clearly such a design implies that each object is weighted
elements equal to zero. Clearly such a design implies that each object is weighted ![]() times in
times in ![]() weighing operations.
weighing operations.
Lemma 3.1. A design given by ![]() of the form (8) is non singular if and only if
of the form (8) is non singular if and only if![]() .
.
Proof. For the design matrix ![]() given by (8), we have
given by (8), we have
![]() (9)
(9)
and
![]() (10)
(10)
the determinant (10) is equal to zero if and only if
![]()
or ![]()
but ![]() is positive and then
is positive and then ![]() if and only if
if and only if ![]() . So the lemma is proved. □
. So the lemma is proved. □
Theorem 3.2. The non-singular chemical balance weighing design with matrix ![]() given by (8) is optimal if and only if
given by (8) is optimal if and only if
![]() (11)
(11)
Proof. From the conditions (5) and (9) it follows that a chemical balance weighing design is optimal if and only if the condition (11) holds. Hence the theorem.
If the chemical balance weighing design given by matrix ![]() of the form (8) is optimal then
of the form (8) is optimal then
![]()
Example 3.3. Consider a SBIB design with parameters![]() ,
, ![]() ,
,![]() ; whose blocks are gi- ven by (3,5,6,7), (1,4,6,7), (1,2,5,7), (1,2,3,6), (2,3,4,7), (1,3,4,5), (2,4,5,6).
; whose blocks are gi- ven by (3,5,6,7), (1,4,6,7), (1,2,5,7), (1,2,3,6), (2,3,4,7), (1,3,4,5), (2,4,5,6).
Theorem 3.2 yields a design matrix ![]() of optimum chemical balance weighing design as
of optimum chemical balance weighing design as
![]()
Clearly such a design implies that each object is weighted ![]() times in
times in ![]() weighing operations and
weighing operations and
![]()
for each.
Corollary 3.4. If the SBIB design exists with parameters![]() ,
, ![]() ,
,![]() ;
;
then the design matrix ![]() so formed using above method is optimum chemical balance weighing design.
so formed using above method is optimum chemical balance weighing design.
Corollary 3.5. If in the design![]() ;
; ![]() is replaced by zero then the new design
is replaced by zero then the new design ![]() so formed is a BIB design with parameters
so formed is a BIB design with parameters![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() . Then the structure
. Then the structure
![]() (12)
(12)
form a pairwise VB and EB design D*1 with parameters
![]() ,
,![]() ,
,![]()
![]()
![]()
4. Construction of Design Matrix: Method II
In SBIB design ![]() with the parameters
with the parameters![]() ,
, ![]() ,
,![]() ; consider the
; consider the ![]() blocks containing any pair of treatments say
blocks containing any pair of treatments say![]() . Now rearranging the
. Now rearranging the ![]() -blocks corresponding to the pair
-blocks corresponding to the pair ![]() and giving the negative sign to the treatments
and giving the negative sign to the treatments ![]() and
and ![]() both; the matrix
both; the matrix ![]() of design
of design ![]() is obtained.
is obtained.
Now doing the same procedure for all the ![]() sets of blocks, the incidence matrix
sets of blocks, the incidence matrix ![]() of the new design
of the new design ![]() so formed is the matrix having the elements 1,
so formed is the matrix having the elements 1, ![]() and 0; given as follows
and 0; given as follows
![]() (13)
(13)
Then combining the incidence matrix ![]() of SBIB design repeated
of SBIB design repeated ![]() -times with
-times with ![]() we get the matrix
we get the matrix ![]() of a chemical balance weighing design as
of a chemical balance weighing design as
![]() (14)
(14)
Under the present construction scheme, we have ![]() and
and![]() . Thus the each column of
. Thus the each column of ![]() will contain
will contain ![]() elements equal to 1,
elements equal to 1, ![]() elements equal to
elements equal to ![]() and
and ![]() elements equal to zero. Clearly such a design implies that each object is weighted
elements equal to zero. Clearly such a design implies that each object is weighted ![]() times in
times in ![]() weighing operations.
weighing operations.
Lemma 4.1. A design given by ![]() of the form (14) is non singular if and only if
of the form (14) is non singular if and only if![]() .
.
Proof. For the design matrix ![]() given by (14), we have
given by (14), we have
![]() (15)
(15)
and
![]() (16)
(16)
the determinant (16) is equal to zero if and only if
![]()
or ![]()
but ![]() is positive and then
is positive and then ![]() if and only if
if and only if ![]() . So the lemma is proved. □
. So the lemma is proved. □
Theorem 4.2. The non-singular chemical balance weighing design with matrix ![]() given by (8) is optimal if and only if
given by (8) is optimal if and only if
![]() (17)
(17)
Proof. From the conditions (5) and (15) it follows that a chemical balance weighing design is optimal if and only if the condition (17) holds. Hence the theorem.
If the chemical balance weighing design given by matrix ![]() of the form (14) is optimal then
of the form (14) is optimal then
![]()
Example 4.3. Consider a SBIB design with parameters![]() ,
, ![]() ,
,![]() ; whose blocks are given by (1,2,4), (2,3,5), (3,4,6), (4,5,7), (1,5,6), (2,6,7), (1,3,7).
; whose blocks are given by (1,2,4), (2,3,5), (3,4,6), (4,5,7), (1,5,6), (2,6,7), (1,3,7).
Theorem 4.2 yields a design matrix ![]() of optimum chemical balance weighing design as
of optimum chemical balance weighing design as
![]()
Clearly such a design implies that each object is weighted ![]() times in
times in ![]() weighing operations and
weighing operations and ![]() for each
for each![]() .
.
Corollary 4.4. If the SBIB design exists with block size ![]() and
and![]() ; then the design matrix
; then the design matrix ![]() so formed using above method II is optimum chemical balance weighing design.
so formed using above method II is optimum chemical balance weighing design.
Corollary 4.5. If the SBIB design exists with parameters![]() ; then the design matrix
; then the design matrix ![]() given by (14) is optimum chemical balance weighing design if and only if
given by (14) is optimum chemical balance weighing design if and only if![]() .
.
Corollary 4.6. If in the design![]() ;
; ![]() is replaced by zero then the new design
is replaced by zero then the new design ![]() so formed is a BIB design with parameters
so formed is a BIB design with parameters![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() . Then the structure
. Then the structure
![]() (18)
(18)
form a pairwise VB and EB design ![]() with parameters
with parameters
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]()
5. A-Optimality of Chemical Balance Weighing Design
Some problems related to the optimality of chemical balance weighing designs were considered in the literature;
see [17] [30] [31] . Wong and Masaro [32] [33] gave the lower bound for ![]() and some construction methods of the A-optimal chemical balance weighing designs.
and some construction methods of the A-optimal chemical balance weighing designs.
Let ![]() be a
be a ![]() design matrix of a chemical balance weighing design. Then the following results from
design matrix of a chemical balance weighing design. Then the following results from
Ceranka et al. [34] give the lower bound for![]() .
.
Theorem 5.1. For any nonsingular chemical balance weighing design with the design matrix ![]() we have
we have
![]() (19)
(19)
where![]() ,
, ![]() ,
,![]() .
.
The case when![]() ; we get the inequality given in Wong and Masaro [32] .
; we get the inequality given in Wong and Masaro [32] .
Definition 5.2. Any nonsingular chemical balance weighing design with the design matrix ![]() is said to be A-optimal if
is said to be A-optimal if
![]() (20)
(20)
Theorem 5.3. Any nonsingular chemical balance weighing design with the design matrix ![]() is A-optimal if and only if
is A-optimal if and only if
![]() (21)
(21)
6. Checking the A-Optimality in Methods I and II
For the construction Method I of chemical balance weighing design; the Lemma 3.1 proven above gave the necessary condition for the design matrix ![]() of the form (8) to be non-singular.
of the form (8) to be non-singular.
Theorem 6.1. The non-singular chemical balance weighing design with matrix ![]() given by (8) is A-optimal if and only if
given by (8) is A-optimal if and only if
![]() (22)
(22)
![]() (23)
(23)
Proof. For the design matrix ![]() given in (8) we have
given in (8) we have
![]()
and
![]()
Comparing these two equalities we get
![]()
and
![]()
If (22) is satisfied then we get the condition (23) from the last equation. Hence the theorem.
For the construction Method II of chemical balance weighing design; the Lemma 4.1 proven above gave the necessary condition for the design matrix ![]() of the form (14) to be non-singular.
of the form (14) to be non-singular.
Theorem 6.2. The non-singular chemical balance weighing design with matrix ![]() given by (14) is A-op- timal if and only if
given by (14) is A-op- timal if and only if
![]() (24)
(24)
and
![]() (25)
(25)
Proof. For the design matrix ![]() given in (14) we have
given in (14) we have
![]()
and
![]()
Comparing these two equalities we get
![]()
and
![]()
If (24) is satisfied then we get the condition (25) from the last equation. Hence the theorem.
7. Discussion
The following Table 1 and Table 2 provide the list of pairwise variance and efficiency balanced block designs for Methods I and II respectively, which can be obtained by using certain known SBIB designs.
8. Conclusion
It is well known that pairwise balanced designs are not always efficiency as well as variance balanced. But in this research we have significantly shown that the proposed pairwise balanced designs are efficiency as well as variance balanced. Further there is a scope to propose different methods of construction to obtain the optimum chemical balance weighing designs and pairwise variance and efficiency balanced block designs, which will ful- fill the optimality criteria by means of efficiency. In this research paper we also gave the conditions under which
**The symbols ![]() and
and ![]() denote the reference number
denote the reference number ![]() in Raghavrao [30] and Marshal Halls [35] list.
in Raghavrao [30] and Marshal Halls [35] list.
the constructed chemical balance weighing designs lead to A-optimal designs. The only limitation of this research is that the obtained pairwise balanced designs all have large number of replications.
Acknowledgments
We are grateful to the anonymous referees for their constructive comments and valuable suggestions.
NOTES
*Corresponding author.