A Survey of the Implementation of Numerical Schemes for the Heat Equation Using Forward Euler in Time ()
1. Introduction
In this paper we have considered the heat equation 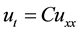 on
on 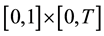 with smooth initial conditions and Dirichlet boundary conditions
with smooth initial conditions and Dirichlet boundary conditions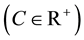 . Using forward Euler in time and fourth order discretization in
. Using forward Euler in time and fourth order discretization in
space, we compute the Global Truncation Error (GTE), the stability restriction on the time step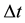 , also we prove consistency and finally we prove the convergence for this scheme.
, also we prove consistency and finally we prove the convergence for this scheme.
Much attention has been paid to the development, analysis and implementation of accurate methods for the numerical solution of this problem in the literature. Many problems are modeled by smooth initial conditions and Dirichlet boundary conditions. A number of procedures have been suggested (see, for instance [1] - [3] ). We can say that three classes of solution techniques have emerged for solution of PDE: the finite difference techniques, the finite element methods and the spectral techniques. The last one has the advantage of high accuracy attained by the resulting discretization for a given number of nodes [4] - [7] . Let 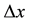 denote the grid-size in the spatial direction and
denote the grid-size in the spatial direction and 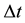 the gridsize in the time direction. By using forward Euler in time, and the fourth order discretization from the previous problem in space, the heat equation reads:
the gridsize in the time direction. By using forward Euler in time, and the fourth order discretization from the previous problem in space, the heat equation reads:
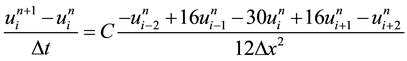 (1)
(1)
We’ll assume that the discretizations used near the boundaries have the same order [8] and [9] .
2. Global Truncation Error (GTE)
There are three equivalent ways of computing the Global Truncation Error for this case.
Way 1. We can always go back to the definition of the GTE. Let 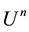 be the true solution at stage
be the true solution at stage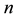 , and
, and 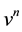 be the solution returned by the scheme at stage
be the solution returned by the scheme at stage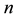 . Therefore
. Therefore
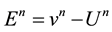 (2)
(2)
We consider de LTE
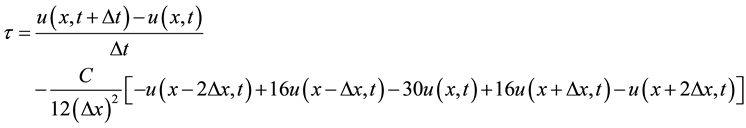 (3)
(3)
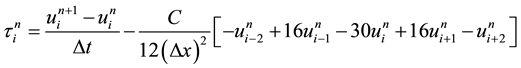 (4)
(4)
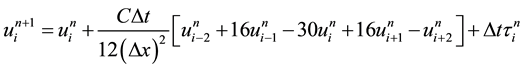 (5)
(5)
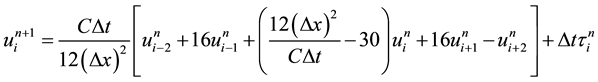 (6)
(6)
![]() (7)
(7)
So that at stage![]() , we have
, we have
![]() (8)
(8)
where
![]() (9)
(9)
![]() is a vector taking care of the boundary conditions and
is a vector taking care of the boundary conditions and ![]() is a matrix. Since
is a matrix. Since
![]() (10)
(10)
we get at stage ![]()
![]() (11)
(11)
![]() (12)
(12)
...
![]() (13)
(13)
![]() (14)
(14)
We now wish to estimate this quantity: first using the triangle inequality, we get
![]() (15)
(15)
Now, taking stability into account, we can see that![]() . Letting
. Letting ![]() we get
we get
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
Now, assuming that initial error is not too large, we have
![]() (19)
(19)
Finally, we can conclude that the ![]()
Way 2. The GTE can be estimated by computing the LTE ![]() and imposing stability to it
and imposing stability to it
![]() (20)
(20)
Way 3. We can also compute the one-step-error for the scheme. This quantity is basically equal to ![]() since it is computed as follows
since it is computed as follows
![]() (21)
(21)
![]() (22)
(22)
then substitute the true solution and compute the difference of the two sides
![]() (24)
(24)
We can then estimate the GTE by summing up the one-step error at each stage
![]() (25)
(25)
![]() (26)
(26)
3. Stability Restriction
We start by computing the stability restriction one has to impose on![]() . We apply Von Neumann stability analysis to the scheme: Letting
. We apply Von Neumann stability analysis to the scheme: Letting ![]() denote the wave number, we get
denote the wave number, we get
![]() (27)
(27)
![]() (28)
(28)
![]() (29)
(29)
![]() (30)
(30)
![]() (31)
(31)
![]() (32)
(32)
then
![]() (33)
(33)
Now, let ![]() and
and
![]() (34)
(34)
So that ![]() when
when![]() . This guarantees that
. This guarantees that![]() . Now, in order to make sure that
. Now, in order to make sure that![]() , we must have
, we must have
![]() (35)
(35)
![]() (36)
(36)
![]() (37)
(37)
![]() (38)
(38)
![]() (39)
(39)
![]() (40)
(40)
4. Consistency and Convergence
We know that a discretization scheme [10] for a PDE is consistent provided that ![]() as
as![]() , where
, where ![]() is the LTE. We compute it by substituting the true solution in the scheme and by using Taylor expansions
is the LTE. We compute it by substituting the true solution in the scheme and by using Taylor expansions
![]() (41)
(41)
![]() (42)
(42)
Thus, ![]() obviously goes to 0 as
obviously goes to 0 as ![]() and
and ![]() go to 0. Therefore, we can say that the scheme is consistent.
go to 0. Therefore, we can say that the scheme is consistent.
Lastly, since we proved that the scheme is consistent and stable, by Lax equivalence theorem, we prove that the scheme is convergent. (By the above, since the GTE is![]() , it goes to 0 as
, it goes to 0 as![]() ). We can see that Lax Equivalence Theorem for PDEs holds provided the scheme is linear (which is the case here). It may not hold for non-linear schemes.
). We can see that Lax Equivalence Theorem for PDEs holds provided the scheme is linear (which is the case here). It may not hold for non-linear schemes.
Another way to get the one-step error for the scheme is to combine the LTE for the temporal and spatial discretization, as follows.
LTE for forward Euler is ![]() and the LTE for the spatial discretization is
and the LTE for the spatial discretization is
![]() (43)
(43)
![]() (44)
(44)
![]() (45)
(45)
This is equivalent to the previous method for getting the one-step error.
Acknowledgements
I would like to thank the referee for his valuable suggestions that improved the presentation of this paper and my gratitude to Department of Mathematics of the Universidad Tecnológica de Pereira (Colombia) and the group GEDNOL.