Theorem of Necessity and Sufficiency of Stable Equilibrium for Generalized Potential Equality between System and Reservoir

Pierfrancesco Palazzo^*

Technip, Rome, Italy.

DOI: 10.4236/jmp.2014.518196                

Abstract

The literature reports that equality of temperature, equality of potential and equality of pressure between a system and a reservoir are necessary conditions for the stable equilibrium of the system-reservoir composite or, in the opposite and equivalent logical inference, that stable equilibrium is a sufficient condition for equality. The aim and the first novelty of the present study is to prove that equality of temperature, potential and pressure is also a sufficient condition for stable equilibrium, in addition to necessity, implying that stable equilibrium is a condition also necessary, in addition to sufficiency, for equality. The second novelty is that the proof of the sufficiency of equality (or the necessity of stable equilibrium) is attained by means of the generalization of the entropy property, derived from the generalization of exergy property, which is used to demonstrate that stable equilibrium is a logical consequence of equality of generalized potential. This proof is underpinned by the Second Law statement and the Maximum-Entropy Principle based on generalized entropy which depends on temperature, potential and pressure of the reservoir. The conclusion, based on these two novel concepts, consists of the theorem of necessity and sufficiency of stable equilibrium for equality of generalized potentials within a composite constituted by a system and a reservoir.

Keywords

Available Energy, Second Law, Stable Equilibrium, Nonequilibrium, Generalized Exergy, Generalized Entropy, Generalized Potential

1. Introduction

The interactions occurring within a composite constituted by a system 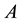and a reservoir determine the state of stable equilibrium which represents the foundation of the Second Law statement reported in the literature and in particular by Gyftopoulos and Beretta [1] . The reservoir is defined as an auxiliary system experiencing stable equilibrium states only [1] . The mutual stable equilibrium between system and reservoir implies the necessary conditions of equal temperature, chemical potential and pressure of the system-reservoir composite 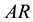[1] . Instead, the canonical definition of entropy, founded on this statement of the Second Law and derived from energy and available energy, is underpinned by the equality of temperature as the sole necessary condition for the stable equilibrium of and for this reason is based only on the constant temperature 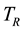of the reservoir [1] . The chemical potential 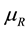and pressure 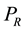of the reservoir do not appear in the formulation of entropy. The first aim is here to explore the possibility of generalizing the definition of exergy property, and consequently the definition of entropy, considering the equality of chemical potential 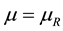and pressure, within the system-reservoir composite, as further necessary conditions of mutual stable equilibrium in addition to equality of temperature and characterizing the definition of generalized entropy by 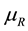and in addition to. 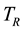The second aim is to demonstrate that equality of temperature, equality of potential and equality of pressure are conditions that are also sufficient for stable equilibrium and the proof is attained by means of the generalized entropy derived from the generalized exergy here defined, which is used to derive stable equilibrium as a logical consequence of the equality of generalized potentials.

The following analysis focuses on “simple systems” according to the terminology and definitions adopted by Gyftopoulos and Beretta [1] where the system can be large or small, even at molecular or atomic level, and can experience states of equilibrium and nonequilibrium [1] [2] . It is important to underline that the present study does not disprove any of the fundamentals reported in the literature, and on the contrary, based on those thermodynamic foundations, it extends the standpoint and generalizes the related definitions and properties.

The method adopted is based on the assumption that entropy is an inherent property of any system [3] and equality of chemical potential and pressure between system and reservoir constitute necessary conditions of stable equilibrium of the system-reservoir composite, in addition to the equality of temperature. These additional conditions will therefore be accounted for in defining of the generalized exergy which implies that generalized entropy is derived according to the procedure based on the statement that entropy 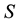is proportional to the difference between energy 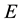and available energy 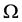[1] according to the following expression:

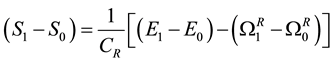(1a)

and considering that the definition of exergy is directly correlated to the generalized available energy consequent to the generalized adiabatic availability [1] , then:

(1b)

in which is a constant property depending on the reservoir only.

2. Thermal Stable Equilibrium as a Sufficient Condition (or Equality of Temperature as a Necessary Condition)

The canonical definition of physical exergy property is based on the amount of heat and work interaction occurring until the system is in a mutual stable equilibrium with the reservoir; in particular, the (thermal) exergy formulated as maximum net useful work, obtained by means of a weight process resulting from the difference of generalized available energy between the (variable) temperature of system and the (constant) temperature of reservoir, is as follows [1] :

(2a)

. (2b)

The term represents the amount of heat released to the reservoir once the equality of temperature between system and reservoir has been achieved at thermal equilibrium.

The term expresses the amount of work released to the reservoir at constant pressure differing from the (variable) pressure of the system, since system and reservoir are not in mutual stable equilibrium even though the system-reservoir composite is in a stable (thermal) equilibrium state due to the equality of temperatures.

According to the procedure reported in the literature [1] , the (thermal) entropy is derived from the product of the factor and the difference between energy and generalized available energy which are both measurable properties while entropy is not:

(3a)

and considering that (thermal) generalized available energy is directly correlated to thermal exergy, then:

. (3b)

It should be noted that this definition of entropy property depends solely on temperature and does not include pressure of the mechanical reservoir despite it is appearing in the definition of thermal exergy expressed by Equations (2a) and (2b) which constitute a term of Equations (3a) and (3b).

Although equality of temperature is a necessary condition of mutual stable equilibrium derived from the Highest-Entropy Principle [1] [4] , this condition is not unique and therefore cannot be also termed sufficient. In fact, even when two interacting systems are in thermal stable equilibrium due to equal temperatures, these systems may experience (constraints removed) states of nonequilibrium due to a not null difference of (chemical) potential and or pressure. Therefore, equality of temperature, chemical potential and pressure between system and reservoir must constitute the set of necessary conditions ensured by the mutual stable equilibrium of a system-reservoir- composite. However, the proof that equal potential and pressure are necessary conditions for stable equilibrium is founded on the Highest-Entropy Principle where the entropy property is defined with respect to a reservoir at constant temperature only [1] [4] . Therefore this Highest-(Thermal)-Entropy Principle should not be able to prove the necessity of potential and pressure because (thermal) entropy does not account for the difference between the potential and pressure of the system and the potential and pressure of the reservoir. Moreover, the procedure adopted to demonstrate the necessity of temperature equality does not explicitly refer to the temperature of reservoir or an intermediate temperature of equality between system and the reservoir at equilibrium. Hence, the definition of (thermal) entropy should require a generalization extended to the contributions of chemical entropy and mechanical entropy evaluated with respect to a reservoir at constant chemical potential and constant pressure adopted in the procedure without any specific constraint of reservoir characteristics [1] .

It is noteworthy that the canonical expression of thermal entropy is proved [1] by means of the concept of impossibility of the Perpetual Motion Machine of the Second Kind (PMM2) which is a consequence of the Second Law expressing the existence and uniqueness of the stable equilibrium state [1] . The thermal aspect of entropy definition proof is based on the impossibility of the PMM2 performing a direct cycle converting an amount of heat interaction into work interaction without releasing heat at lower temperature to a thermal reservoir.

3. Chemical Stable Equilibrium as a Sufficient Condition (or Equality of Potential as a Necessary Condition)

A definition of chemical exergy is proposed by Kotas [5] as “the maximum work obtainable from a substance when it is brought from the environmental state to the dead state by means of processes involving interaction only with the environment”. Indeed, such an environment is a system behaving as a chemical reservoir which can be characterized according to the definition proposed by Gyftopoulos and Beretta [1] as a “reservoir with variable amounts of constituents”. The maximum net useful work withdrawn from the system interacting with the reservoir undergoing a process from initial state 0 to final state 1, corresponding to the chemical exergy, is expressed by the following equation reported by Kotas [5] :

(4)

where the superscript “C” stands for “chemical reservoir” since the composite of system and reservoir under- goes an interaction that can be defined as “mass interaction” determining a “useful work” until the system- reservoir composite is not in a state of stable equilibrium. Mass interaction is characteristic of chemical energy transfer and it is moved by the difference of chemical potential between the system and the chemical (isopotential) reservoir.

In the more general case of a mixture consisting of chemical constituents, according to the definition reported by Moran and Sciubba [6] :

(5)

where represents the molar fraction of the constituent. The equality of chemical potentials is accounted for as a further necessary condition of mutual stable equilibrium between the system and the reservoir in addition to the equality of temperature [1] . This implies a definition of chemical entropy derived from chemical exergy and chemical energy according to the method previously adopted and the general definition of Equations (1a) and (1b). To do so, if the concept of generalized available (chemical) energy is again considered, the formulation of chemical exergy should be translated as the following expression:

(6a)

. (6b)

Now that chemical exergy is defined, and considering that energy and available energy are additive properties, chemical entropy is an additive property as well. Therefore, chemical entropy may be derived from the chemical potential and the generalized available (chemical) energy which depends on mass interaction:

(7a)

and considering that a correlation between generalized chemical available energy and chemical exergy can be established:

(7b)

which expresses the chemical entropy derived from (chemical) energy and chemical exergy, based on the equality of potential that constitutes a necessary condition for mutual stable equilibrium between the system and the chemical reservoir, in addition to equality of temperature [1] . This expression depends on the potential of reservoir and is formally analogous to the thermal entropy Equation (3a) and (3b). The term corresponds to the term in Equations (2a) and (2b), so that chemical stable equilibrium is the result of the necessary condition of chemical potential equality between the system and chemical reservoir, given the equality of temperature and pressure of the system-reservoir composite.

4. Mechanical Stable Equilibrium as a Sufficient Condition (or Equality of Pressure as a Necessary Condition)

The weight process constitutes a device adopted to measure the maximum net useful work extracted from a system releasing a corresponding minimum non-useful heat to a (thermal) reservoir at constant temperature according to the definition of generalized available energy and thermal exergy here adopted. The inverse (and reversible) process requires the weight process to be the minimum net useful work released to and extracting a corresponding maximum non-useful heat from. Nevertheless, the weight process can also

be regarded as an interaction suitable for calculating the minimum non-useful work, released by

system to the (mechanical) reservoir at constant pressure, associated to the maximum net useful

heat which, in this symmetric process, can be referred to as mechanical exergy [7] . In this

case, the weight process occurs through the interaction of system with mechanical reservoir until the difference of pressure between system and reservoir is null. Due to the fact that the non-useful work is released interacting with the mechanical reservoir, it may be inferred that work, such as heat, is no longer useful since it constitutes the non-convertible component of generalized available energy of the system interacting with the mechanical reservoir.

To summarize, the mechanical exergy property accounts for the maximum net useful heat ex-

tracted from system releasing the minimum non-useful work to the mechanical reservoir. System interacts with a mechanical reservoir behaving as an isobaric reservoir. Then, with the symbol adopting the superscript “M” standing for “mechanical”:

(8a)

. (8b)

This relation expresses the amount of generalized available (mechanical) energy of system converted into

heat interaction at higher variable temperature with respect to the thermal reservoir at lower constant temperature. On the other hand, results from the minimum amount of work interaction released to the mechanical reservoir along the isothermal process where the heat interaction is withdrawn from the thermal reservoir to be converted into. The minimum amount of non-useful

work interaction, corresponding to the maximum net useful heat withdrawn, at constant temperature, from the thermal reservoir and converted into useful heat at higher temperature, is expressed as follows:

. (9)

The term equals the (theoretically minimum) amount of work released to the reservoir and is equal to the low temperature heat, withdrawn from the thermal reservoir, converted

into high temperature heat.

The definition of mechanical exergy formulated by Equations (8a) and (8b) is the basis for deriving the expression on mechanical entropy using the same procedure adopted for thermal exergy and thermal entropy:

(10a)

taking into account the relationship between generalized mechanical available energy and mechanical exergy:

. (10b)

Equation (9), substituted in the former relation, implies the expression of mechanical entropy [7] :

. (11)

This expression is a consequence of the Second Law and the stable equilibrium state in a system-reservoir composite AR. The condition of pressure equality between system and reservoir might prove, using the Highest- (Mechanical)-Entropy Principle, to be an additional necessary condition of mutual stable equilibrium between system and reservoir that needs to be complied, with the equality of temperature and potential to ensure the equilibrium status of the composite system-reservoir as a whole.

The Second Law implies the impossibility of a Perpetual Motion Machine of the Second Kind (PMM2) performing, in this case, an inverse cycle so that it may be expressed as the impossibility for available energy to be transferred from a reservoir at lower pressure to a system at higher pressure without the contribution of heat interaction. This inverse PMM2 can consequently represent a statement to prove mechanical entropy definition by using the same method adopted to derive the entropy property from the Second Law principle.

5. Generalized Entropy Derived from Generalized Exergy

The definition of exergy is characterized by the property of additivity because it is defined with respect to an external reference system or to an internal part of the system itself behaving as a reservoir. The definition of a thermo-chemical-mechanical reservoir characterized by constant temperature, chemical potential and pressure implies the property of additivity of the components that constitute the generalized exergy so that:

. (12)

The additivity of the entropy property can be proved considering the additivity of energy and generalized available energy. On the basis of the additivity of the entropy property, the generalized entropy results from the sum of entropy components each derived from the corresponding exergy component related to the (generalized) potential constituted by temperature, chemical potential and pressure. Therefore, generalized entropy can be expressed as [8] :

. (13)

Generalized entropy is derivable from generalized exergy if, and only if, the system is in stable equilibrium with a generalized reservoir. This condition implies equality of temperature, chemical potential and pressure between system and reservoir which becomes a set of necessary conditions for the stable equilibrium state of the system-reservoir composite.

6. Stable Equilibrium as a Necessary and Sufficient Condition for Generalized Potential Equality

One of the most recent statements of the Second Law consists of the existence and uniqueness of stable equilibrium [1] [9] . This statement implies that all subsystems of a whole system have to be individually in stable equilibrium and the composite of all subsystems mutually interacting with each other has to be in stable equilibrium as well. On the other hand, entropy property is a consequence of the Second Law founded on stable equilibrium which implies that equality of potential and equality of pressure are additional necessary conditions consequent to stable equilibrium, however potential and pressure of the reservoir do not appear in the definition of entropy property mentioned above. In fact, the formulation of entropy here referred to, is correlated solely to the equality of temperature between system and reservoir and indeed depends solely on the temperature of reservoir. As a further consideration, the proof that potential and pressure are additional necessary conditions of stable equilibrium is based on the Highest-Entropy Principle whereas the definition of entropy is related to equality of temperature only and does not include potential and pressure [1] . The reason is that the proof is general, while the concept of entropy has not been generalized as well to comply with the proof procedure. Therefore, there is an apparent inconsistency which may be resolved by means of a generalization of the entropy definition proposed in the previous section.

According to the proof theory, deriving a thesis from a hypothesis leads to the logical proof of hypothesis sufficiency and, vice versa, deriving the hypothesis from the thesis leads to the logical proof of hypothesis necessity.

The proof that equality of temperatures, potentials and pressures within the whole composite system-reservoir are necessary condition of stable equilibrium, hence “equilibrium => equality”, is described by Gyftopoulos and Beretta [1] who adopt the Highest-Entropy Principle to prove that temperature-potential-pressure equality is the consequence of individual-and-interacting stable equilibrium [1] [10] .

With an opposite logical procedure, Gaggioli adopts the Lowest-Energy Principle to prove that individual- and-interacting stable equilibrium implies temperature-potential-pressure equality [11] . Therefore stable equilibrium is a sufficient condition for equality, hence, once again, “equilibrium => equality”. However, since sufficiency of equilibrium (or necessity of equality) is the sole condition established and proved and, on the other hand, the necessity of stable equilibrium is not proved, then the system-reservoir composite may experience equality of the temperatures, potentials and pressures while the composite itself is not in a stable (or neutral) equilibrium state since the equilibrium is not necessary as well (or equality is not sufficient as well) in contradiction to the assumed stable equilibrium. To resolve this contradiction, reference can be made to the thermal, chemical, mechanical contributions of exergy, which is an additive property, so that the sum of these contributions constitutes generalized exergy as the base for deriving generalized entropy, which is an additive property as well, as demonstrated in Section 5 above. The only procedure to prove the necessity and sufficiency, without disproving the proofs already provided in the literature, is consequently to demonstrate that equalities (or equilibrium) are necessary and sufficient conditions, thus Gaggioli’s statement is also necessary and Gyftopoulos and Beretta’s statement is also sufficient, both implying that the inference equality => equilibrium is complementary to the inference equilibrium => equality so that both equilibrium and equality are necessary and sufficient conditions for each other. In different terms, equilibrium is true if and only if equality is true and equality is true if and only if equilibrium is true. Figure 1 represents the hierarchical structure of the statement of necessity and sufficiency conditions.

Thus, Gaggioli adopts the Lowest-Energy Principle and Gyftopoulos and Beretta adopt the Highest-Entropy Principle, and since entropy depends on the difference between energy and generalized available energy as per Equations (1a) and (1b) which imply the First Law and Second Law respectively, then entropy remains the suitable quantity to attain the proofs of sufficiency as well as necessity. Therefore entropy property should account for potential and pressure, in addition to temperature in order to constitute the procedure for such a proof. Lowest-Energy Principle ó Highest-Entropy Principle. The two principles are mutually correlated to each other. In fact, the Stable-Equilibrium-State Principle establishes the mathematical relationship among all system properties. This relationship also exists between the Lowest-Energy Principle and the Highest-Entropy Principle which are intrinsic to the Stable-Equilibrium-State Principle as stated by the fundamental relations as follows [1] :

(14a)

. (14b)

The proof of the necessity of stable equilibrium (or the sufficiency of generalized potential equality) consists of deriving stable equilibrium from equality and may be established “ab absurdum” assuming that temperatures, potentials and pressures of system and reservoir are equal while the system-reservoir composite is not in stable equilibrium. Indeed, this condition is admitted by the sufficiency of stable equilibrium as the only inference which does not “necessarily” imply that stable equilibrium is a consequence of equality of temperature, potential and pressure in the system-reservoir composite so that the equality may be compatible with nonequilibrium. This equality of generalized potential would thus be able to move the system into a nonequilibrium state without undergoing any net change of the environment, or that would be able to generate a weight process according to a PMM2 which is impossible according to the Second Law statement based on stable equilibrium as assumed. The consequence is that equality must imply stable equilibrium, that is, equality must be a sufficient condition for stable equilibrium (or stable equilibrium must be a necessary condition for equality). The proof of this sufficiency can be based on the Highest-Generalized-Entropy Principle where generalized entropy depends on

Figure 1. Hierarchical structure of necessity and sufficiency conditions.

temperature, potential and pressure of reservoir.

Having assumed the equality of generalized potential between system and reservoir, generalized entropy has to assume the highest value and the system is thus at stable equilibrium.

7. Conclusion

The result of the present study is a proposal to encompass the Second Law statement by a bi-univocal logical relationship between the stable equilibrium of a system-reservoir composite assumed as a hypothesis, and generalized potential equality derived as the thesis of a theorem. The outset is that the literature reports the equality of temperature, potential and pressure between a system and a reservoir as a necessary condition for stable equilibrium of the system-reservoir composite or, in the opposite and equivalent logical inference, that stable equilibrium is a sufficient condition for equality. The method adopted consists of the analysis of the logical relationship between stable equilibrium and equality of generalized potential correlated by the Maximum-Entropy Principle. The first conclusion is the proof that equality of temperature, potential and pressure is also a sufficient condition, in addition to being necessary, for stable equilibrium implying that stable equilibrium is also a necessary condition, in addition to being sufficient, for equality of generalized potential. The second conclusion is that the proof is attained by means of the generalized entropy derived from the generalized exergy here defined, which is used to demonstrate that stable equilibrium is a logical consequence of equality of generalized potentials. This proof is underpinned by the Second Law statement conceived in terms of existence and uniqueness of stable equilibrium and using the Maximum-Generalized-Entropy Principle based on generalized entropy property which depends on the temperature, potential and pressure of the reservoir. The conclusion, derived from these two novel concepts, consists of the theorem of necessity and sufficiency of stable equilibrium for equality of generalized potentials within a composite constituted by a system and a reservoir.

Nomenclatures

: System;

: System-reservoir;

: Composite;

: Energy, J;

: Exergy, J;

: Gibbs potential, J;

: Mass, Kg;

: Constituent;

: Pressure, Pa;

: Heat interaction, J;

: Reservoir;

: Universal gas constant;

: Entropy, J/K;

: Temperature, K;

: Internal energy, J;

: Volume, cubic m;

: Work interaction, J;

: Mole.

Greek Symbols

: Chemical potential, J;

: Available energy, J.

Subscripts and Superscripts

: Composite system-reservoir;

: Chemical;

: Generalized;

: Mass;

: Maximum;

: Minimum;

: Net;

: Reservoir;

: Reversible;

: Thermal;

: Initial state;

: Final state;

: Outward interaction flow;

: Inward interaction flow.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Gyftopoulos, E. and Beretta, G.P. (2005) Thermodynamics: Foundations and Applications. Dover Publications, New York.
[2]	Beretta, G.P. (2008) International Journal of Thermodynamics, 11, 39-48.
[3]	Gyftopoulos, E.P. (2006) International Journal of Thermodynamics, 9, 107-115.
[4]	Zanchini, E. (2000) International Journal of Thermal Sciences, 39, 110-116. http://dx.doi.org/10.1016/S1290-0729(00)00196-3
[5]	Kotas, T.J. (1995) The Exergy Method of Thermal Plant Analysis. Reprint Edition, Krieger Publishing Company, Malabar.
[6]	Moran, M.J. and Sciubba, E. (1994) Journal of Engineering for Gas Turbine and Power, 116, 285-290. http://dx.doi.org/10.1115/1.2906818
[7]	Palazzo, P. (2012) International Journal of Energy and Environmental Engineering, 3, 4. http://dx.doi.org/10.1186/2251-6832-3-4
[8]	Palazzo, P. (2013) Journal of Modern Physics, 4, 52-58. http://dx.doi.org/10.4236/jmp.2013.47A2008
[9]	Zanchini, E. and Beretta, G.P. (2010) International Journal of Thermodynamics, 13, 67-76.
[10]	Zanchini, E. and Barletta, A. (1995) Il Nuovo Cimento, 110B, 10.
[11]	Gaggioli, R.A. (1998) International Journal of Applied Thermodynamics, 1, 1-8.