1. Introduction
The series S(x), where
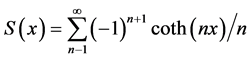 (1)
(1)
does not appear in any of several compendiums of infinite series or products [1] -[4] . The author first encountered it for x = π, as part of a solution to an electrostatics boundary-value problem, and he deduced a simple analytic expression for S(π) based on the known solution to this problem in a limiting case. This is opposed to a “first-principles” derivation. The problem involves the determination of the electrical resistivity of a uniform material in the shape of a thin square of side “a” and thickness c, as c → 0. This situation arises in the semiconductor industry in the electrical characterization of blank wafers of materials, such as silicon, within which numerous circuits are fabricated.
The particular measurement configuration considered here is shown in Figure 1.
Depicted in this figure there is a square sample of side “a” and a square contact array of semi-diameter w, rotated by 45˚ with respect to the sample and displaced from the center of the sample by the vector s. This displacement can be in any direction and magnitude as long as the array remains completely within the sample (including on the boundary). Current Io is forced to enter contact 1 and leave contact 2, and the resulting potential difference between contacts 4 and 3, ∆φ = φ4 − φ3, is determined from a voltage measurement. Mathematically, the contacts are considered point-like, which in practice means that their diameter ≤W (the same is also true for c). The practical purpose of solving the boundary-value is to determine the voltage and thus the stability of the results with respect to the displacement and w [5] . In [5] , these results were compared to those associated with a non-rotated array. When s = 0 and w/a = 1/2, we obtain the situation shown in Figure 2, where all four contacts are on the boundary in a highly symmetric arrangement.
This is a special case of the more general one considered by van der Pauw [6] in a seminal paper in which neither the sample nor the contact array is required to have any simple shape, only that the sample be thin, have no holes in it, and that all contacts are point-like and on its periphery. He used the method of conformal mapping, not the electrostatics method of [5] . For the particular configuration in Figure 2, his results reduce to:
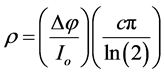 (2)
(2)
![]()
Figure 1. General configuration of the electrostatics boundary-value problem that led to the series in question.
![]()
Figure 2. The limiting case of the configuration in Figure 1, or the symmetric van der Pauw arrangement, satisfied by Equation (5). The current and voltage points are not shown.
In this equation, ρ is the electrical resistivity. When w/a < 1/2 and s ≠ 0, Equation (2) must be modified, such that:
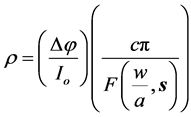 (3)
(3)
Clearly, F(1/2, 0) = ln(2). The function F(w/a, s) was calculated in [5] using a standard separation-of-va- riables technique applied to Laplace’s equation for the potential everywhere within the sample, along with the appropriate surface boundary conditions on its gradient. The function F(w/a, 0) is as follows:
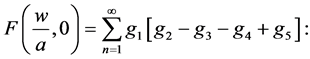 (4)
(4)


![]()
![]()
![]()
Allowing w/a = 1/2, we obtain, after considering even and odd n separately:
![]() (5)
(5)
Using the relationship [4] :
![]() (6)
(6)
and F(1/2, 0) = ln(2), we obtain:
![]() (7)
(7)
It is clear that the sum in Equation (7) should be very close to ln(2) because coth(nπ) → 1 so quickly with n. In fact, the right-hand side of Equation (7) is 0.6968×××, while ln(2) = 0.6931×××, resulting in a percentage difference of about 0.5%. When the left-hand side was summed directly, the two sides agreed to the limit of precision of the software used, or 15 significant figures.
2. Alternate Derivation for Several Values of x
The above derivation is based on a requirement of a physics problem and applies to only one value of x, x = π. The following derivation, which applies to an array of values of x, proceeds by recasting the series in a different form and applying certain existing relationships to evaluate the resulting series.
Using the definition of the hyperbolic cotangent, we rewrite S(x) as:
![]() (8)
(8)
This series can be expressed in a more useful form for our current purpose. We first note that for![]() ,
, ![]() , where the sum is from k = 0 to k = ∞, and that
, where the sum is from k = 0 to k = ∞, and that![]() , where
, where ![]() and the sum is from m = 1 to m = ∞. In this case,
and the sum is from m = 1 to m = ∞. In this case, ![]() and z = 1. Consequently, after a few simple manipulations, we can express S(x) as:
and z = 1. Consequently, after a few simple manipulations, we can express S(x) as:
![]() (9)
(9)
For certain values of x, the series can now be evaluated in a straightforward manner, using existing relationships.
3. Evaluation of the Series
These relationships are stated in [4] (“Series of Logarithms” and “Specific Values” of “Series Expansion of Inverse Elliptical Nome Q”). Obtained from “Series of Logarithms” is the most fundamental of these relationships for our purpose:
![]() (10)
(10)
In this expression, q is the elliptical nome [7] and m is the inverse elliptical nome (0 < m < 1). In the second section of [4] , certain values of q are stated along with their associated m. All of these expressions for q are of the form:![]() , where λ is real and >0 (this must be true of λ, based on the definition of q in [7] ). Thus, if we are to use these results, x = πλ/2, although it is not clear why or if x must be some multiple of π to obtain an analytic expression for S(x). Since Equation (10) is fundamental to the evaluation of S(x), some background information concerning it is called for. First, it is equivalent to:
, where λ is real and >0 (this must be true of λ, based on the definition of q in [7] ). Thus, if we are to use these results, x = πλ/2, although it is not clear why or if x must be some multiple of π to obtain an analytic expression for S(x). Since Equation (10) is fundamental to the evaluation of S(x), some background information concerning it is called for. First, it is equivalent to:
![]() (11)
(11)
Second, in [4] under “Inverse Elliptic Nome Q m[q] and K [m[q]] Expressed through Infinite Products” are the following relationships:
![]() (12)
(12)
Using this equation to form the right-hand side of Equation (11) easily leads to its left-hand side, after a few simple algebraic manipulations. The equality between the first and second terms in Equation (12) is discussed in [8] , while that between the first and third is discussed in [9] .
Also in the second section of [4] are three relationships that allow us to expand the number of values of x ad infinitum. These relationships are as follows:
![]() (13)
(13)
or its inverse,
![]() (14)
(14)
and
![]() (15)
(15)
The first of these three equations allows one to generate the inverse nome of q2, given the inverse nome of q, and that of q4 from that of q2, etc. From Equation (14), the inverse nome of q1/2, q1/4, etc. can be generated starting with that of q. Thus, starting with a particular value of X, say X0, one can generate an entire array of X, say Xn, to which Equation (10) can be applied, such that:
![]() (16)
(16)
By using Equation (15), which follows directly from the definition of elliptical nome in [7] (ch. 17), one can generate additional values of X0 through the inverse of λ (i.e., X0 = πλ/2 → X0 = π/2λ). This has been done for a few cases in [4] . It also follows directly from Equation (15) that m = 1/2 for λ = 1.
4. Examples of Closed-Form Solutions
A few examples of the use of these equations to generate closed-form expressions for S(x) will now be presented. They will be for λ = 1/2, 1, 2, and 4, which corresponds to x = π/4, π/2, π, and 2π, respectively. Since the value of S(x) for x = π motivated this entire undertaking, it is included here. Starting with λ = 1, for which m = 1/2, one can use Equation (14) to generate the value of m for λ = 1/2 and Equation (16) to generate m for λ = 2 and 4. The value of m for λ = 1/2 can also be generated from the value of m for λ = 2, using Equation (15). All of these results are actually presented in [4] . The other starting values of λ in [4] that have been used to generate the remaining results are: ![]() and
and![]() .
.
![]()
![]() (17)
(17)
![]()
![]() (18)
(18)
![]()
![]() (19)
(19)
![]()
![]() (20)
(20)
![]()
![]() (21)
(21)
![]()
![]() (22)
(22)
![]()
![]() (23)
(23)
![]()
![]() (24)
(24)
All of these results (and others not shown) have been confirmed by an agreement with a direct summation of each series. Figure 3 is a graphical representation S(x) vs. x/π. We note that, as expected, S(x) rapidly approaches ln(2) with increasing x. At the other extreme, S(x) → ∞ as (1/x) for small x. The inset in Figure 3 demonstrates this behavior on a log-log plot.
![]()
Figure 3. Graphical representation of the results of this study. The inset is a log-log scale in which the dotted line is an eyeball fit.
5. Conclusion
Simple analytic formulas have been produced for eight values of x for the series![]() , where the sum is from n = 1 to n = ∞, although the sum could also be over the negative integers. These values are a subset of a much larger set of x for this possible. This larger set obviously encompasses the corresponding negative values of x. The formulas were produced by recasting the series into a form such that known relationships involving the elliptical nome could be applied to their derivation. The author first encountered the series for x = π in an electrostatics boundary-value problem. The sum for this value of x was the result of the application of the series to a limiting case of that problem. This value of x was also one of the eight just mentioned. It is quite possible that this series, with the appropriate values of x, is at least part of the solution of other physical problems.
, where the sum is from n = 1 to n = ∞, although the sum could also be over the negative integers. These values are a subset of a much larger set of x for this possible. This larger set obviously encompasses the corresponding negative values of x. The formulas were produced by recasting the series into a form such that known relationships involving the elliptical nome could be applied to their derivation. The author first encountered the series for x = π in an electrostatics boundary-value problem. The sum for this value of x was the result of the application of the series to a limiting case of that problem. This value of x was also one of the eight just mentioned. It is quite possible that this series, with the appropriate values of x, is at least part of the solution of other physical problems.
Acknowledgements
The author is grateful to J. Mercer of Albuquerque, New Mexico for reviewing the manuscript and making valuable suggestions for its improvement. This work was self-funded.