On Universal Mechanics and Superluminal Velocities

Caesar P. Viazminsky¹, Piere K. Vizminiska²

¹Department of Physics, Illinois Institute of Technology (IIT), Chicago, USA.
²Department of Computer Engineering, University of Detroit Mercy, Detroit, USA.

DOI: 10.4236/am.2014.517260                

Abstract

In this work we continue to set up the theory of universal space and time and derive the Euclidean form of the scaling transformations. Two types of velocities emerge, inertial and universal, with the former bound by the light velocity c whereas the latter is unbound, and may accommodate consistently particles’ velocities possibly exceeding c. The inertial velocity is the ratio of the simultaneous source’s displacement and the corresponding length of the light trip to the observer, whereas the universal velocity has its familiar meaning for motion in a synchronous inertial frame. Defining the momentum as the product of universal velocity and mass, and utilizing the already established mass-energy equivalence, the mechanics constructed on the bases of the new concepts, named universal mechanics, admits superluminal velocities but yet coincides with the relativistic mechanics in its basic dynamical components and their inter-relations. The possibility of superluminal velocities provides a straight forward explanation of the presence of the μ-meson particles abundantly at the sea level despite their generation at high altitude and their short lifetime.

Keywords

Inertial Velocity, Superluminal Speeds, Universal Mechanics

1. Introduction

The basic concepts and main structure of the theory of the universal space and time (UST) were discussed in [1] . It was argued that time intervals are essentially measured by spatial intervals associated with light trips. A light trip follows the same path in the universal space which can be identified with any inertial frame, one at a time. The duration and direction of a light trip are the same, but its geometric lengths differ from a frame to another. The scaling transformations (STs) determine the relation between the geometric lengths of the same light trip in two inertial frames. The STs were shown to map intrinsic units in a frame on intrinsic units in another, and were utilized to explain the presence of the 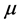-meson particles which are generated at a high latitude at the sea level despite their short lifetime. It was also shown that in UST the longitudinal Doppler’s effect coincides with the relativistic one, but the transverse effect at right angle is absolutely absent in UST.

In the current work which continues constructing UST we furnish the following points:

· We derive the scaling transformations in a concise and transparent way illuminating its Euclidean form.

· Two types of velocity are distinguished, inertial and universal, with the former bound by light velocity, while the latter is unbound and can exceed c.

· The inertial velocity is defined by the quotient of the distance travelled by a body to the corresponding distance travelled by a light pulse. The universal velocity is the quotient of the distance travelled by the body to the corresponding time interval in a universal space.

· Defining the particle’s momentum by the product of its mass and universal velocity, we obtain all basic relativistic mechanical expressions and relations [2] -[6] .

· The paradox of the presence of the meta-stable particles at sea level finds its natural explanation in superluminal speeds of these particles.

In future works, the change of direction of a light trip between two frames and its application to explain the stellar aberration will be presented. Also, a second type of scaling transformation (STII) will be derived and applied to explain the drag effect, Sagnac effect, Michelson and Morley experiment, Michelson and Gale experiment.

2. The Euclidean Form of the Scaling Transformations

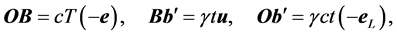(2.1)

satisfy the relation

Figure 1. The light’s trips to stationary and moving targets as seen from two frames when each is considered universal.

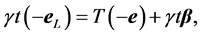(2.2)

where 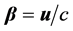Solving for 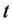we obtain

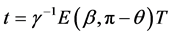, (2.3)

where

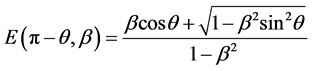(2.4)

We shall call 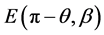the Euclidean factor.

Since time in the UST theory is a frame-independent entity we therefore seek the transformation from a universal frame 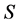to a frame 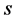co-moving with 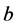such that the transformation and its inverse yield time durations as frame-independent. The latter demand is essential to enable one to start with either 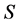or a frame co-moving with (but not both) as universal. 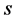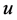Consider thus an inertial frame moving in the universal frame at velocity; the body will be at rest in. Let be the -observer that is contiguous to at the instant, i.e., when the spherical wave emanates from. While remains at rest in the moving frame, the body moves at velocity. In the frame, the wave hits at the instant and intercepts at the instant at a position. We seek thus the transformation that maps the triangle in to the triangle in, with the time lengths of and are equal to the time lengths of and respectively, and vice versa. Since the role of the ordered pair in s must be identical to the role of the pair in, the relation between and in must results from that in by interchanging and in (2.3) and replacing by or equivalently by. This yields

. (2.5)

On the other hand, the quantities and already satisfy (2.3). Substituting one of the Equations (2.3) or (2.5) in the other yields

(2.6)

or

(2.7)

The required transformation is therefore

(2.8a)

or

. (2.8b)

We call the function the scaling factor and the relation the scaling transformation (ST). The relation (2.8b) is called the Euclidean form of the scaling transformation. The inverse of the latter relation is obtained through interchanging and and replacing by (or by) which amounts to (2.8) itself. The ST allows for each frame to be taken stationary, and it holds within the same frame whether it was the stationary or the moving frame, as well as between the universal and moving frame. Note that the geometric lengths of the corresponding trips in S and s are different.

It was shown in [1] that if a light wave emanates from when at then the period it takes to arrive at is also given by (2.8), i.e. if a light wave emanates from simultaneously with a wave emanating from then when the former arrives at, the latter arrives at.

3. The Euclidean Body-Observer Triangle

The initial and final positions of the moving body in the universal frame together with the observer’s position form a Euclidean triangle (Figure 2) with sides length’s

. (3.1)

The given lengths satisfy all triangle relations in Euclidean geometry, and yield a value for the time duration as it is prescribed by the STI. An elementary fact asserts that when three numbers are legitimate to form a triangle, this triangle is unique (up of course to arbitrary rotations, translations, or reflections). Thus the latter values determine a unique Euclidean triangle; it is the body-observer triangle.

By (3.1) we have

, (3.2)

which are equivalent to the relations

(3.3)

In terms of the initial geometric distance T we have

. (3.4)

By the sinuses law in trigonometry,

, (3.5)

we have

(3.6)

By (3.2) the pair of sides are in 1-1 correspondence with the pair, and the body-observer triangle is thus determined by. This expresses the obvious fact that the direction of the vector relative to the observer, i.e., is determinable by the quantities through the scaling transformations, by which we can determine one out of the quantities in terms of the remaining three. In other words, the body-observer triangle is fully determined by three out of the four variables.

Figure 2. The body-observer triangle.

This implies that, in correspondence with each body-observer triangle there is one value of, and hence the same value of is obtained whether calculated from the expressions of or or from the STI.

The Inertial Velocity: By (3.2), the displacement of the source, the distance travelled by the signal, and their duration are in 1-1 correspondence. The quantity

(3.7)

which is obtained from (3.2), will be called the inertial velocity of the body. The definition (3.7) expresses the inertial speed in terms of geometric distances; it is the quotient of the distance travelled by the body to the distance travelled by the light emanating from the observer when they intercept each other. The initial time for both motions is the instant (at). By [1] , is also the distance travelled by the pulse emitted from when at till arriving at.

4. The Universal Mechanics

The universal velocity of a body refers to its velocity in a universal space; it is defined exactly as the familiar velocity in classical mechanics:

(4.1)

The universal velocity of the body b is

(4.2)

where by (3.2)

. (4.3)

It is clear that tends to zero with and it can assume any non-negative value with no upper bound.

The momentum of the particle is defined by the product of its mass and universal velocity:

(4.4)

Multiplying both sides of the identity

, (4.5)

by we obtain

(4.6)

In the reduced system of units () [1] , mass, energy and momentum are all measured by the same unit, kilogram. Thus, the right hand-side of (4.6) can be envisaged as a difference between the squares of two values of the mass or energy of the moving body corresponding to the states of motion and rest respectively. Denoting these values by and respectively, i.e.,

, (4.7)

we write (4.6) in the form

(4.8)

The latter relation reads: the state of motion of a body with rest mass that is characterized by a momentum of magnitude is accompanied by a total energy, or kinetic mass,

. (4.9)

When goes to zero, the total energy (or kinetic mass) tends to the rest energy (or rest mass). The Hamiltonian of the particle coincides with its total energy:

(4.10)

In MKM,. The force acting on a particle is defined as in Newtonian mechanics by the time rate of the change in its momentum:

(4.11)

If the magnitude of remains constant while its direction changes,

(4.12a)

If only the magnitude of changes while its direction remains constant,

. (4.12b)

If both the magnitude and direction of change then

(4.13)

Differentiating both sides of the equation with respect to time, we obtain

. (4.14)

The relation (4.14) determines the instantaneous rate at which the mass changes under the action of a force when moving at velocity. Looking on as the total energy of the particle, the Equation (4.14) also determines the power of the force, i.e. the rate at which it does work. The work done by the force during a displacement is given by

. (4.15)

It is customary to measure mass in kg, energy in, and momentum in, which corresponds to using the reduced system of units in which the expressions (4.7) become

(4.16)

And Equations (4.9) and (4.10) become

, (4.17)

. (4.18)

The Equation (4.14) which gives the rate of kinetic energy change is written as follows

. (4.19)

And the work done by the force during a displacement is written as

. (4.20)

From its definition, the momentum of a particle is related to its universal velocity and energy by

. (4.21)

Or equivalently

. (4.22)

For particles travelling at a universal velocity, we have

(4.23)

We recall that is unbound in magnitude, and hence, the value is attainable. For such particles

(4.24)

The energy needed to give a stationary particle a universal velocity is

In the relations (4.21) and (4.23) the rest energy (or rest mass) is directly measurable, and the momentum of the particle is known if the body’s velocity is known. For particles that can exist only in a state of motion, like photons in vacuum, it is meaningless to talk in, which is the observer frame, about the photon’s rest mass or rest energy. However, the relation (4.21), written in terms of inertial velocity

(4.25)

and applicable to material particle, may be extended to comprise photons whose velocity is in. For material particles, both and are determined on knowing and, which are immediately measurable. Setting in the latter relation we obtain for photons

(4.26)

Unlike the relation (4.23) which connects directly measurable quantities, the latter relation which extends (4.25) to photons, requires in order to be fully meaningful a way by which either the energy or the momentum of a photon is prescribed. It is not satisfactory to merely deduce the energy and the momentum of the photon through its earlier or subsequent interaction with an external system. The contrary is required; the theory should be capable to quantify the photon’s energy and momentum in terms of inherent characteristics, and thus capable of predicting the magnitudes of its interaction with an external system. Moreover, and whereas (4.23) assigns to a particle with a rest energy a definite momentum, the relation (4.25) does not distinguish between photons; it only states the relation between their energy and momentum. The additional information about the energy and momentum of a photon comes from Plank hypothesis which relate the energy (or momentum) of a photon to a macroscopic measurable quantity, the frequency of photon, by (or).

5. Point-Wise Measurement of the Inertial Velocity

Suppose that the free source of light is detected at a point at and at at an instant of time. The pulse which was emitted from when was at arrives at the instant at. i.e., the arrivals of at and the pulse at are simultaneous; they both occur at. Let be the geometric length of the displacement. The source, at the time, is at geometric distance

(5.1)

from. This yields

(5.2)

The latter formula determines the inertial velocity of a moving body in in terms of the time read at its final position and the geometric distance of from the body’s initial position. The Formula (5.2) digresses from the Newtonian (or universal) definition of the velocity as the ratio of distance travelled to the corresponding time interval, which takes in our units the form. In terms of the universal velocity, the inertial velocity takes the form

(5.3)

The following comments illustrate some facts concerning the inertial velocity which applies, of course, only to material bodies, but not to light signals.

(i) By (5.2), , and hence the inertial velocity cannot reach velocity of light.

(ii) If a body is at rest at which is distinct from, then will never be found at. Setting in (5.2) yields.

(iii) In spite of the fact that the inertial velocity of any object cannot reach the velocity of light, the object itself can overtake the pulse emanating from its starting position. If the moving body and the light signal emitted from when passed by, arrive simultaneously at, then, and the inertial ve-

locity of the body is. However, the universal velocity of the same body is.

While inertial velocity cannot reach the velocity of light, universal velocity is unbound. These facts demonstrate that there is nothing odd about the result of an experiment yielding a superluminal speed for an elementary particle.

(iv) For a fixed value of, is a decreasing function of; it tends to zero for tending to infinity and to 1 for tending to zero. This expresses the obvious fact, the faster the particle is the shorter time it takes to arrive at.

(v) For small velocities, and

(5.4)

If the inertial velocity is sufficiently small we can neglect the third order term in comparison with the first order term and write

(5.5)

We also obtain the same result simply by neglecting 1 in the dominator on the right hand-side of (5.2) in comparison with the much larger term Therefore, for small values, the classical expression is an approximation of the inertial velocity Formula (5.2).

For high velocities, and the Formula (5.2) can be approximated by

(5.6)

The inertial velocity can also be deduced in terms of Indeed, on solving the expression of for we obtain the following equivalent expression of the inertial velocity,

(5.7)

The -meson particles lifetime once more

The -meson particles whose mean lifetime is, are generated at about 60 km above the earth surface, that is,. Inserting in Formula (5.2) yields the inertial velocity of the particles that just arrive at the earth surface as

(5.8)

The particles with inertial velocities not less than the latter value can cover 60 km in the earth’s frame in spite of the fact that a pulse of light emitted from an -observer can travel during the period of the -meson lifetime only

(5.9)

Relative to the earth frame the universal velocity of the mesons particles that reach the earth surface is

(5.10)

one hundred times of the velocity of light!

6. The Simultaneous Positions of a Particle and Its Emitted Signal

Suppose that the body heads towards with inertial velocity. A pulse emitted from when at, say at, arrives at simultaneously with the body arriving at. The Galilean picture in which light is envisaged to emanate from the body’s current position, corresponds to body-observer triangle (3.1), which reduces in the current head-on motion to a 3 straight segments (Figure 3), with

(6.1)

Equivalently,

(6.2)

The first and third ratios show that when the body is at a distance from, the pulse it emits is at a distance

Figure 3. The simultaneous positions of the moving body and its emitted signal.

(6.3)

from. Thus, a particle always lacks behind the pulse it emits in its direction. As an example, a hypothetical light signal emitted from the meson particles when generated, travels by the time during which a meson particle arrives at the earth surface the distance

which (assuming not absorbed) is almost twice as much the distance travelled by the particle itself.

By (6.1), the particle and the light, arrive at, at and respectively, where

(6.4)

(6.5)

Thus light arrives first at advancing by

(6.6)

Employing the STI to determine the position of the light front when arrives at; i.e. at the instant of time, we get

(6.7)

which coincides with (6.3). The same relation has been obtained by the Galilean picture, which on scaling

and yields the particle travelling the distance with velocity and light travelling the distance with velocity 1. i.e.

Substituting for from (6.4) we obtain as given by (6.3). On changing to distances instead of geometric time distances we write (7.3) in the form

which is the same as the classical picture, apart from the fact that the quotients are, but not, and hence refers to the inertial velocity. For small velocities, , and.

7. Conclusion

The UST which was shown to produce the mass-energy equivalence relation in a natural way proved also capable of producing a universal mechanics that is almost identical to the relativistic mechanics. Indeed, and through defining momentum as the product of mass and universal velocity, which has no upper bound, the mechanics constructed admits superluminal velocities but yet coincides with the relativistic mechanics in its basic dynamical components and their inter-relations. The possibility of superluminal velocities provides a straight forward explanation of the abundant presence of the -meson particles at the sea level in spite of their generation at high latitude and their short lifetime.

NOTES

^*This is an extended version of the paper: C. P. Viazminsky and P. K. Vizminiska, “On Universal Mechanics and Superluminal Velocities in ST”, Jan. 9, 2014, General Sciences Journal.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Viazminsky, C.P. and Vizminiska, P.K. (2014) On Universal Space and Time. Applied Mathematics, 5, 2530-2546. http://dx.doi.org/10.4236/am.2014.516243
[2]	Rindler, W. (1977) Essential Relativity. Springer-Verlag, New York. http://dx.doi.org/10.1007/978-3-642-86650-0
[3]	French, A.P. (1968) Special Relativity. Butler & Tanner Ltd., Frome and London.
[4]	Steve, A. (1997) Relativity: An Introduction to Space-Time Physics. Taylor and Francis Ltd., London.
[5]	Landau, L.D. and Lifshitz, E.M. (1980) The Classical Theory of Fields. Pergamon Press, Oxford.
[6]	Mould, R.A. (1998) Basic Relativity. Springer-Verlag, London.