Local Empirical Likelihood Diagnosis of Varying Coefficient Density-Ratio Models Based on Case-Control Data

Shuling Wang¹, Lin Zheng², Jiangtao Dai³

¹Department of Fundamental Course, Air Force Logistics College, Xuzhou, China.
²School of Statistics and Applied Mathematics, Anhui University of Finance and Economics, Bengbu, China.
³Fundamental Science Department, North China Institute of Astronautic Engineering, Langfang, China.

DOI: 10.4236/ojs.2014.49070                

Abstract

In this paper, a varying-coefficient density-ratio model for case-control studies is developed. We investigate the local empirical likelihood diagnosis of varying coefficient density-ratio model for case-control data. The local empirical log-likelihood ratios for the nonparametric coefficient functions are introduced. First, the estimation equations based on empirical likelihood method are established. Then, a few of diagnostic statistics are proposed. At last, we also examine the performance of proposed method for finite sample sizes through simulation studies.

Keywords

Varying-Coefficient Density-Ratio Model, Local Empirical Likelihood, Outliers, Influence Analysis

1. Introduction

Varying coefficient models are often used as extensions of classical linear models (e.g. Shumway [1] ). Their appeals are that the modeling bias can be significantly reduced and the “curse of dimensionality” can also be avoided. These models have gained considerable attention due to their various applications in many areas, such as biomedical study, finance, econometrics, and environmental study. The estimation for the coefficient functions has been extensively discussed in the literatures, including the smoothing spline method (see Hastie and Tibshirani [2] ), the locally weighted polynomial method (see Hoover et al. [3] ), the two-step estimation procedure (see Fan and Zhang [4] ), and the basis function approximations (see Huang et al. [5] ).

In this paper, we consider the following general two-sample varying-coefficient density-ratio model

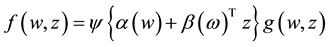(1)

where 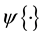is a nonnegative known function that makes to be a density function, which includes the exponential-tilt model as a special case with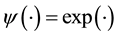. In parametric situation, Thomas [6] and Lustbader

et al. [7] considered a general relative risk model, a mixture model, ,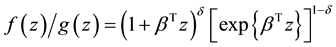

where 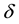is a scalar parameter that describes the general shape of the relative risk function. It includes additive relative risk model 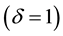and log-linear relative model 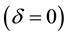as special cases.

Various density-ratio models for some conventional density functions were discussed in Kay and Little [8] . It has been shown recently that the density-ratio model provides a good fit to the observed data in some medical applications (Qin and Zhang [9] ; Qin et al. [10] ; Zhang [11] ), genetic quantitative trait loci analysis (Zou et al. [12] ), and clinical trials with skewed outcomes (White and Thompson [13] ). Liu, Jiang and Zhou [14] considered estimation and inference for the two-sample varying-coefficient density-ratio model (1) by constructing the local empirical likelihood function. The EL approach is appealing for analyzing the varying-coefficient density-ratio model because the two density functions in (1) can be modeled nonparametrically. This nonparametric method of inference has sampling properties similar to the bootstrap. Another advantage of the EL approach is that it takes auxiliary information, such as the density-ratio in (1), into account to improve estimation.

The empirical likelihood method origins from Thomas & Grunkemeier [15] . Owen [16] first proposed the definition of empirical likelihood and expounded the system info of empirical likelihood. Zhu and Ibrahim [17] utilized this method for statistical diagnostic. Liugen Xue and Lixing Zhu [18] summarized the application of this method.

Over the last several decades, the diagnosis and influence analysis of linear regression model has been fully developed (R.D. Cook and S. Weisberg [19] , Bocheng Wei, Gobin Lu & Jianqing Shi [20] ). Regarding the varying coefficient model, especially for the B-spline estimation of parameter, diagnosis and influence analysis have some results (Z. Cai, J. Fan, R. Li [21] , J. Fan, W. Zhang [22] ). So far the statistical diagnostics of varying- coefficient density-ratio models with case-control data based on local empirical likelihood method has not yet seen in the literature. This paper attempts to study it.

The remainder of the article is organized as follows. Local empirical likelihood and estimation equation are presented in Section 2. The main results are given in Section 3. An example is given to illustrate our results in Section 4.

2. Local Empirical Likelihood and Estimation Equation

Let 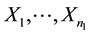be a sequence of independent and identically distributed random vectors from the control group, each with density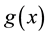, and 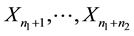be a sequence of independent and identically distributed random vectors from the case group, each with density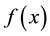, 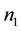and 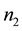are the number of subjects in the control

group and case group, respectively. Let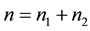, and 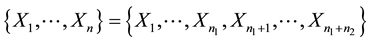denote

the pooled sample. Assume that as. From model (1), the empirical likelihood function derived according to Prentice and Pyke [23] is:

(2)

where, and is the distribution func-

tion corresponding to. However, can not be used directly to obtain estimates for and because and are infinite-dimensional parameters. Thus, instead of (2), we consider the localized conditional empirical likelihood below.

Assume that all components of and are smooth so that they admit Taylors series expansions, i.e., for each given and for around,

(3)

Let, and. For simplicity,

denote by and by for fixed. Then, the local log empirical likelihood (LEL) function of is

where is the weight with kernel function and

represents the size of the local neighborhood. The kernel weight is used to give smoother weight to data with near. The last constraint is the auxiliary information for the EL estimation. By the method of Lagrange multipliers, similar to that used in Owen (2001), we obtain

where is determined by the constraint equation

.

Motivated by Zhu and Ibrahim (2008), we regard and as independent variables and define

.

Obviously, the maximum empirical likelihood estimates and are the solutions of following equations:

3. Local Influence Analysis of Model

We consider the local influence method for a case-weight perturbation, for which the empirical log-likelihood function is defined by. In this case, , defined to be an vector with all elements equal to 1, represents no perturbation to the empirical likelihood, because. Thus, the empirical likelihood displacement is defined as, where is the maximum empirical likelihood estimator of based on. Let with and, where is a direction in. Thus, the normal curvature of the influence graph is given by, where

,

in which is a matrix with -th element given by.

We consider two local influence measures based on the normal curvature as follows. Let

be the ordered eigenvalues of the matrix and let

be the associated orthonormal basis, that is,. Thus, the spectral decomposition of is given by

.

The most popular local influence measures include, which corresponds the largest eigenvalue, as well

as, where is an vector with -th component 1 and 0 otherwise. The represents

the most influential perturbation to the empirical likelihood function, whereas the -th observation with a large can be regarded as influential.

As the discuss of Zhu et al. (2008), for varying-coefficient density-ratio model, we can deduce that

(4)

where

4. Numerical StudyWe generate

We generate and from two densities and, respectively. We setboth densities and to be trivariate normal distributions, in which, is a scalar,, and

Figure 1. The influence value of.

are trivariate normal densities with means and, and inverses of the covariances

Because, we have

, and.

We draw 1000 data sets with sample size for various values of. We

choose the Epanechnikov kernel to localize the coefficient functions.

In order to checkout the validity of our proposed methodology, we change the value of the first, 125th, 374th,

789th and 999th data. For every case, it is easy to obtain. For and, using the sam-

ples, we evaluated their maximum empirical likelihood estimators.

Consequently, it is easy to calculate the value of and. The result of is as following Figure 1.

It can be seen from the result of that the first, 125th, 374th, 789th and 999th data are strong influence points. Indeed, our results are illustrated.

5. Discussion

In this paper, we considered the statistical diagnosis for varying-coefficient density-ratio model based on local empirical likelihood. Through simulation study, we illustrate that our proposed method can work fairly well.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Shumway, R.H. (1988) Applied Statistical Time Series Analysis. Prentice-Hall, Englewood Cliffs.
[2]	Hastie, T.J. and Tibshirani, T. (1993) Varying-Coefficient Models. Journal of the Royal Statistical Society, 55, 757-796.
[3]	Hoover, D.R., Rice, J.A., Wu, C.O. and Yang, L.P. (1998) Nonparametric Smoothing Estimates of Time-Varying Coefficient Models with Longitudinal Data. Biometrika, 85, 809-822. http://dx.doi.org/10.1093/biomet/85.4.809
[4]	Fan, J.Q. and Zhang, W.Y. (1999) Statistical Estimation in Varying-Coefficient Models. Annals of Statistics, 27, 1491-1518. http://dx.doi.org/10.1214/aos/1017939139
[5]	Huang, J.Z., Wu, C.O. and Zhou, L. (2004) Polynomial Spline Estimation and Inference for Varying Coefficient Models with Longitudinal Data. Statistica Sinica, 14, 763-788.
[6]	Thomas, D.C. (1981) General Relative-Risk Models for Survival Time and Matched Case-Control Analysis. Biometrics, 37, 673-686. http://dx.doi.org/10.2307/2530149
[7]	Lustbader, E.D., Moolgavkar, S.H. and Venzon, D.J. (1984) Tests of the Null Hypothesis in Case-Control Studies. Biometrics, 40, 1017-1024. http://dx.doi.org/10.2307/2531152
[8]	Kay, R. and Little, S. (1987) Transformations of the Explanatory Variables in the Logistic Regression Model for Binary Data. Biometrika, 74, 495-501. http://dx.doi.org/10.1093/biomet/74.3.495
[9]	Qin, J. and Zhang, B. (1997) A Goodness-of-It Test for Logistic Regression Models Based on Case-Control Data. Biometrika, 84, 609-618. http://dx.doi.org/10.1093/biomet/84.3.609
[10]	Qin, J., Berwick, M., Ashbolt, R., et al. (2002) Quantifying the Change of Melanoma Incidence by Breslow Thickness. Biometrics, 58, 665-670. http://dx.doi.org/10.1111/j.0006-341X.2002.00665.x
[11]	Zhang, B. (2001) A Information Matrix Test for Logistic Regression Models Based on Case-Control Data. Biometrika, 88, 921-932. http://dx.doi.org/10.1093/biomet/88.4.921
[12]	Zou, F., Fine, J.P. and Yandell, B.S. (2002) On Empirical Likelihood for a Semiparametric Mixture Model. Biometrika, 89, 61-75. http://dx.doi.org/10.1093/biomet/89.1.61
[13]	White, I.R. and Thompson, S.G. (2003) Choice of Test for Comparing Two Groups, with Particular Application to Skewed Outcomes. Statistics in Medicine, 22, 1205-1215.
[14]	Liu, X., Jiang, H. and Zhou, Y. (2013) Local Empirical Likelihood Inference for Varying-Coefficient Density-Ratio Models Based on Case-Control Data. Journal of the American Statistical Association, 109, 635-646. http://dx.doi.org/10.1080/01621459.2013.858629
[15]	Thomas, D.R. and Grunkemeier, G.L. (1975) Confidence Interval Estimation of Survival Interval Estimation of Survival Probabilities for Censored Data. Journal of the American Statistical Association, 70, 865-871. http://dx.doi.org/10.1080/01621459.1975.10480315
[16]	Owen, A. (2001) Empirical Likelihood. Chapman and Hall, New York. http://dx.doi.org/10.1201/9781420036152
[17]	Zhu, H.T., Ibrahim, J.G., Tang, N.S and Zhang, H. (2008) Diagnostic Measures for Empirical Likelihood of Generalized Estimating Equations. Biometrika, 95, 489-507. http://dx.doi.org/10.1093/biomet/asm094
[18]	Xue, L. and Zhu, L. (2010) Empirical Likelihood in Nonparametric and Semiparametric Models. Science Press, Beijing.
[19]	Cook, R.D. and Weisberg, S. (1982) Residuals and Influence in Regression. Chapman and Hall, New York.
[20]	Wei, B., Lu, G. and Shi, J. (1990) Statistical Diagnostics. Publishing House of Southeast University, Nanjing.
[21]	Cai, Z., Fan, J. and Li, R. (2000) Efficient Estimation and Inferences for Varying-Coefficient Models. Journal of American Statistical Association, 95, 888-902. http://dx.doi.org/10.1080/01621459.2000.10474280
[22]	Fan, J. and Zhang, W. (2008) Statistical Methods with Varying Coefficient Models. Statistics and Its Interface, 1, 179-195. http://dx.doi.org/10.4310/SII.2008.v1.n1.a15
[23]	Prentice, R.L. and Pyke, R. (1979) Logistic Disease Incidence Models and Case-Control Studies. Biometrika, 66, 403-411. http://dx.doi.org/10.1093/biomet/66.3.403