Circular Scale of Time and Energy of a Quantum State Calculated from the Schrödinger Perturbation Theory ()
1. Introduction. Time Notion and Its Subjective Character
Time notion penetrates our everyday life and this penetration concerns obviously the science, too. In a science whose attempt is to be exact―and physics can be an example of such science―we like to do measurements on the physical quantities and compare the results with those of other measurements of a similar kind. When a sufficiently extended background of measurements is attained, an idea or concept concerning the measured quantity, or quantities, can be developed. A subjective character of our knowledge on time obtained in this way is almost evident.
For example a well-known property of an atom of a non-radiative element being in its ground state―and left free from any external perturbation or influence―is that this atom remains unchanged for an arbitrarily long interval of time. If an observer can examine only the objects composed of such atoms, he will never get an idea on time because there exists no parameter to develop such an idea. This is so because a basic necessary condition to establish the notion of time is a change. If there is no change in the observed system, the time scale of such a system is reduced to a single (constant) point.
In practice, however, the human nature of an observer grown up in the everyday life leads him a priori to a well-established notion of time and its scale. This comes from the fact that any human being is influenced by observations in which the change plays a dominant role. As an effect of these observations we get a notion of time as a label of a sequence of events extended between a very distant past and a very distant future. Evidently, this is a commonly accepted idea which penetrated also into science. In consequence, the events are usually classified along a scale of time which is considered as a line extended from an infinitely distant past labelled by
 (1)
(1)
to an infinitely distant future
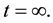 (2)
(2)
The present situation can be classified as being connected with
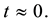 (3)
(3)
Evidently, such a scale is a well-established notion in classical physics including the statistics and special theory of relativity.
But a different scale of events leading to a different scale of time may be also of use. Let us return to an atom described by the old quantum theory, for example a hydrogen atom. In this picture the electron in the atom is circulating about the nucleus in a plane. When considered with respect to some constant direction in that plane, the electron in effect of its circulation process is returning incessibly to its original position which it had before the time period
 (4)
(4)
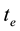 is the the end time and
is the the end time and 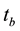 is the beginning time of a single circulation period.
is the beginning time of a single circulation period.
Having some measured, or calculated, T there is no way in the atom to distinguish how many circulations have been done before the time interval given in (4), and how many will be done after (4). The whole situation of the atomic electron repeats with T with no possibility to count, or distinguish, different circulation time periods in the system.
If the observer’s ability is of the same character as the property of the observed atom, the beginning time of the next circulation becomes identical with the end time of the former circulation. Since for any circulation the difference between the end time and the beginning time is limited by the same T, the set of events in the atom can be plotted along a scale having a finite length T. Because the end time on that scale merges with the beginning time of the next circulation, we can call the scale a circular scale of time.
The problem of the time scale applied in quantum mechanics is briefly discussed in Section 2. In fact the time scale of this discipline does not differ much from that applied in classical physics and the everyday life. The aim of the paper is to point out that for the perturbation problem met in quantum mechanics it becomes much more useful to develop a time scale which is different than a classical one. A new scale is a mixture of the progressive scale applied in the classical physics and a circular scale of time.
2. Time Scale in Quantum Mechanics
A look on quantum mechanics indicates that the time scale applied in it can depend on the kind of the examined problem. For example for a stationary state of an atomic system a point-time, or zero-time, scale mentioned at the beginning of Section 1 can be a suitable notion. This is so because quantum mechanics rejects the idea of electrons circulating periodically about the atomic nucleus if the atom is in its stationary state. This attitude is, in the first step, a consequence of the duality property of the electron which is a combination of the particle behaviour and the behaviour characteristic for the matter wave. In the next step, the uncertainty connected with description of the electron position and momentum in a stationary quantum state should be taken into account. Because the electron energy in a stationary state is strictly defined, this energy―combined with a definite potential―gives a known electron momentum for any place in the atom. In consequence, the uncertainty principle concerning the observables of position and momentum of an electron eliminates the possibility to define the electron position in the atom at all.
Evidently, the point-like or zero-time scale cannot be accepted when the atomic changes are present. The changes can be due to the atom interaction with some external forces and effects, for example light, radiation, sound, fields of the external potential sets, etc. Other changes can be due to the interactions between the atoms themselves.
The importance of the atom perturbations has been understood already at the beginning of quantum mechanics. In effect a successful formalism for a treatment of a special kind of perturbations, namely those which are independent of time, has been developed by Schrödinger [1] , one of founders of the quantum-mechanical ideas. Since by hypothesis the time parameter did not enter the perturbations, the Schrödinger formalism for the perturbations could avoid the notion of the time at all. Nevertheless, more than twenty years after the Schrödinger’s approach, Feynman’s idea of classification of the quantum events with respect to time became in vogue [2] . This included also the Schrödinger perturbation theory for the time-independent problems.
The properties of the time scale applied by Feynman were translated into the language of diagrams [3] in which the line going up is coupled with an increase of the time variable, whereas the line going down means a decrease of that variable. Since there is no limit imposed on the time variable, the scale of time applied by Feynman is essentially identical to that of the classical physical theory: it is extended between the limits represented by the formulae of (1) and (2).
In Section 3, the use of the Feynman approach in calculating the perturbation energy of a quantum system is examined. This examination shows that the time scale applied by Feynman is not a suitable tool in a treatment of the system perturbation.
3. Time Scale Applied by Feynmann and the Perturbation Energy of a Non-Degenerate Quantum State
An important point is to couple the time scale with the perturbation energy of a system which is
 (5)
(5)
This ΔE should be added to the original unperturbed energy E0 of a system in order to obtain the system energy Eper after perturbation:
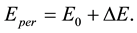 (6)
(6)
A single non-degenerate quantum state n can be submitted to perturbation, so we assume that
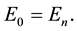 (7)
(7)
The perturbation is an effect of the action of a time-independent perturbation potential
 (8)
(8)
which is dependent solely on the coordinates of the spatial position vector r.
The Schrödinger perturbation terms entering ΔE in (6) can be classified according to the number of collisions of a quantum system with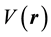 . A single collision with
. A single collision with 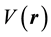 gives the only component ΔE1 entering ΔE, two collisions with
gives the only component ΔE1 entering ΔE, two collisions with 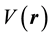 give the components proving us with ΔE2, three collisions―the components belonging to ΔE3, finally N collisions with
give the components proving us with ΔE2, three collisions―the components belonging to ΔE3, finally N collisions with 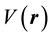 give the energy components belonging to ΔEN. Therefore, if the Nth order perturbation is assumed to be a sufficiently accurate approximation to represent ΔE, we obtain
give the energy components belonging to ΔEN. Therefore, if the Nth order perturbation is assumed to be a sufficiently accurate approximation to represent ΔE, we obtain
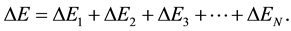 (9)
(9)
But a well-known fact on the terms ΔEi entering (9) having
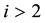 (10)
(10)
is that the terms belonging to the same i can be of a different kind. The number of kinds of the perturbation terms for i = N is labelled by SN given by the formula [4] [5]
![]() (11)
(11)
With the increase of N increases not only SN (see Table 1), but increases also complication of the individual terms entering the set of SN. This property makes the calculation of the perturbation terms for large N an extremely complicated task. Nevertheless, the large orders of the perturbation terms can enter into quantum physics; see e.g. Feynman’s Nobel lecture [6] .
A difficulty with the choice of the scale of time suitable for the quantum perturbation theory arises from the fact that an approach to ΔEN with the aid of the Feynman diagrams requires the number of diagrams larger than (11) namely [3]
![]() (12)
(12)
For small N we have approximately
![]() (13)
(13)
but for ![]() it is easy to show (see Table 1) that
it is easy to show (see Table 1) that
![]() (14)
(14)
This is a very serious obstacle because for large N a huge number of PN terms of energy corresponding to PN Feynman diagrams should be first calculated, and next combined in the SN energy terms defining ΔEN. For example for N = 20, we have
![]() (15)
(15)
which means that, in average, about 108 perturbation terms descending from the Feynman diagrams P20 should be combined into one S20 term. A programming of such a task may be difficult even with the use of the modern computers.
But this situation can be changed by a choice of the scale of time different than the straight-linear one applied in the classical physics and the Feynman theory, too. This is topologically a circular scale of time which implies that the time variable used to calculations is advancing not on a line extended from minus to plus infinity but along a topological circle, or a set of circles [7] -[9] . An important property of such choice of scale is that the number of circle-like diagrams necessary to obtain a given ΔEN becomes precisely equal to SN.
4. Main Properties of the Circular Scale of Time Referred to the Schrödinger Perturbation Terms and Partition Properties of the Perturbation Order N
A characteristic point is that
![]() (16)
(16)
and this single term of the perturbation theory obtained for N = 1 is represented by a diagram being a single topological circle; see Figure 1(a). The only point of time defined on this diagram is the beginning-end point of a circular scale; no other special time points have to be considered.
![]()
Table 1. Recurrence formulae for Si [10] .
![]()
Figure 1. Diagrams denoting the Schrödinger perturbation terms for N = 1, 2, 3 and 4.
But a similar circular diagram is valid as a time scale for any perturbation order N, in this case N time points are presented on the diagram; see Figure 1(b) for N = 2, Figure 1(c) for N = 3, Figure 1(e) for N = 4. An essential step is to find the remainder of
![]() (17)
(17)
diagrams which belong to N. A general rule applied in this case is to perform contractions between the N − 1 time points present on the circle in such a manner that the lines obtained between the time points do not cross. One of the N time points, called the beginning-end point of the scale, is assumed to be not submitted to contractions. Such a treatment has been performed before [7] -[9] giving precisely the SN − 1 diagrams due to contractions. Together with a single diagram which is free of contractions, the total number of diagrams belonging to the order N becomes equal to SN.
The aim of the present paper is to give an algebraic guide to the diagrams obtained in the way outlined above. Some attempt of this kind has been done earlier [10] giving a recurrence formula for SN. The formula is obtained by noting that any N > 1 can be submitted to partition into two components:
![]() (18)
(18)
If all partitions of the kind of (18) are considered, the recurrence formula for calculating SN from SN' and SN'' having
![]() (19)
(19)
is based on a sum of all products of SN' and SN'' for which the relation of (18), namely
![]() (20)
(20)
is satisfied. Examples of such calculation are given in Table 1.
But a different kind of partition of N than (18) useful in calculating ΔEN does also exist. Let us take for example N = 5 and separate the number of 1 representing a single beginning-end point of time on the circular scale. The following eight partitions are then obtained:
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
![]() (25)
(25)
![]() (26)
(26)
![]() (27)
(27)
![]() (28)
(28)
The numbers on the right in (21)-(28) which are larger than 1 have been taken into brackets because of a special meaning which can be associated with them. Namely (2) after a single 1 means that two successive points are taken after the beginning-end point and contracted together, (3) after a single 1 means that three successive points after the beginning-end point are taken into account and the first of them is contracted necessarily with the third point, etc. If the number in brackets is coming after several numbers 1 before it, it means that contraction is done after several points of time. For example (2) in the formula (24) means that contraction is done between the third and fourth point of time after the beginning-end point because there are two numbers 1 after the 1 entering the head of the row in (24) and representing the beginning-end point of the scale. Only single contractions indicated by one colon (:) are considered in this way in (22)-(24), multiple contractions, which enter (26)-(28), are separately discussed below.
Let us note that
![]() (29)
(29)
and next substitute
![]() (30)
(30)
When all terms Si obtained in this way on the right of (21)-(28) are next multiplied, we obtain respectively the products:
![]() (21a)
(21a)
![]() (22a)
(22a)
![]() (23a)
(23a)
![]() (24a)
(24a)
![]() (25a)
(25a)
![]() (26a)
(26a)
![]() (27a)
(27a)
![]() (28a)
(28a)
An important result is obtained in effect of summation of (21a)-(28a):
![]() (31)
(31)
because (31) is equal to (see Table 1)
![]() (32)
(32)
Therefore the partition process of N = 5 performed in (21)-(28) leads to SN of (32). The energy ΔE5 is calculated in Section 4 and presented in a compact form in Table 2. In Table 3 and Table 4, we perform the partition processes for N = 6 and N = 7, respectively; in fact the processes can be abbreviated to ![]() and
and![]() . The result is similar to that in (32), for
. The result is similar to that in (32), for
![]() (33)
(33)
in the case of Table 3 and
![]() (34)
(34)
![]()
Table 2. Low-order perturbation energies (from N = 1 to N = 5) calculated for a non-degenerate quantum state.
![]()
Table 3. Partitions of N − 1 = 6 − 1 = 5 associated with calculation of ΔE6. The products of Si, where i label the component numbers entering partition, are also presented (Sprod). The sum of all Sprod is equal to SN = S6.
in the case of Table 4. This implies that grouping and separations of the time points done on diagrams finds its counterpart in the partition process of N.
In effect of contractions of the time points on a single-circle diagram, the multi-circle diagrams arise beginning with N = 3; see Figure 1(c) and Figure 1(d). Let us label the points on the scale by 1, 2, 3. One of points, say 3, is the beginning-end point and this point does not enter in contractions. But the remaining points 1 and 2 can form a contraction which is labelled by
![]()
Table 4. Partitions of N − 1 = 7 − 1 = 6 associated with calculation of ΔE7. The products of Si, where i label the component numbers entering partition, are also presented (Sprod). The sum of all Sprod is equal to SN = S7.
![]() (35)
(35)
Therefore for N = 3 can exist only a single multi-circle diagram (which is in fact a two-circle diagram) in accordance with the result of S3 = 2 for the total number of diagrams: one diagram has no time contractions and there is only one diagram which has a contraction of the time points which are 1 and 2.
Evidently for N = 1 no contraction is possible because no other points beyond a single point, which is the beginning-end point, are represented on the scale. In the next step, for N = 2 [see Figure 1(b)], we have two points on a single-circle scale, but one point is the beginning-end point and as such it cannot be submitted to contraction with the other point. The five diagrams of N = 4 ![]() are presented in (e), (f), (g), (h) and (i) of Figure 1, the diagrams belonging to N = 5 are discussed in Section 4.
are presented in (e), (f), (g), (h) and (i) of Figure 1, the diagrams belonging to N = 5 are discussed in Section 4.
An extension of the contraction procedure and diagrams for N > 5 has been done elsewhere; see [7] -[9] . In all cases the number of diagrams obtained in effect of contractions, increased by the presence of one uncontracted diagram for each N, agrees with the number SN.
5. The Path of Time on the Diagrams and Calculation of the Schrödinger Perturbation Terms
If the path of time is extended along the loops of time present on the diagrams, any of the Schrödinger perturbation terms known from the time-independent perturbation theory can be obtained in effect of an integration along the diagrams with the accuracy to the sign [8] [9] [11] . For n being the quantum state submitted to perturbation, the summations known from the Schrödinger perturbation theory run over the indices labelling the unperturbed states different than n. On the time scale this means that a repetition of a circular path of time for different sets of the unperturbed quantum states
![]() (36)
(36)
submitted to summations should be done.
The sign of the energy term is defined by the number of loops entering the diagram suitable for that term. If the number of loops is![]() , the sign of term is defined by the factor
, the sign of term is defined by the factor
![]() (37)
(37)
An application of the theory in calculating ![]() for
for ![]() is given below.
is given below.
6. Perturbation Energy of order N = 5 and Similar Energies of Order N Smaller than 5
With the aid of (21)-(28) the calculation of the perturbation energy ΔE5 taken as an example can be a simple task. The partition (21) is corresponding to the one-loop diagram having the beginning-end point of the scale; see diagram (a) in Figure 2. The energy term associated with (21) is
![]() (38)
(38)
where any
![]() (39)
(39)
is the matrix element between the unperturbed quantum states a and b. The summations over p, q, r, s done in (38) (and below) do not involve index n denoting the quantum state submitted to perturbation.
The energy terms corresponding to (22), (23) and (24) are associated, respectively, with single contractions
![]() (40)
(40)
see diagrams (b), (c), (d) in Figure 2. These contractions give
![]() (41)
(41)
for 1:2,
![]()
Figure 2. Diagrams denoting the Schrödinger perturbation terms for N = 5.
![]() (42)
(42)
for 2:3,
![]() (43)
(43)
for 3:4. By symmetry the term in (41) is equal to that in (43).
Formula (25) gives two contractions on the main loop of time denoted by
![]() (44)
(44)
see diagram (e) in Figure 2. Such diagram is composed of three loops (the main loop and two side loops). It gives the energy term
![]() (45)
(45)
In the next step each of partitions entering (26) and (27) gives two-loops and three-loops diagrams defined, respectively, by contractions
![]() (46)
(46)
in case of (26) [diagrams (f) and (h) in Figure 2], and contractions
![]() (47)
(47)
in case of (27) [diagrams (g) and (i) in Figure 2]. The energy terms due to the above contractions are
![]() (48)
(48)
for 1:3,
![]() (49)
(49)
for 1:2:3,
![]() (50)
(50)
for 2:4,
![]() (51)
(51)
for 2:3:4. For symmetry reasons characteristic for the energy formulae, (48) is equal to (50) and (49) is equal to (51).
There remains still contraction
![]() (52)
(52)
represented by the number (4) entering formula (28); see also diagrams (j), (k), (l), (m) and (n) on Figure 2. The contraction in (52) implies a separation of the main loop of time from the side loop having four points on it (the contraction 1:4 and free points 2 and 3); see diagram (j). But 2 and 3 can be next contracted giving a single point
![]() (53)
(53)
represented by the diagram (k). In effect (52) and (53) together are represented on (k) by a combined contraction
![]() (54)
(54)
When (54) is combined with contraction (52) alone, both contractions (52) and (54) represent the diagrams characteristic for ΔE3. By taking into account that there exists also the main loop for the whole partition (28) irrelevant to contractions done in (52) and (54), the contributions to ΔE5 given by (52) and (54) [diagrams (j) and (k)] can be joined into one term equal to:
![]() (55)
(55)
in this term the energy coming from two diagrams is combined into the factor ΔE3. But ![]() and
and![]() , so
, so
![]() (56)
(56)
and we should still take three perturbation terms into account.
Since the beginning-end point of a side loop of time can be submitted to contractions with other points, the lacking terms (56) connected with partition (28) are given by contractions
![]() (57)
(57)
[diagrams (l), (m) and (n) on Figure 2].
The contraction 1:2:4 gives
![]() (58)
(58)
the contraction 1:3:4 gives the result
![]() (59)
(59)
equal to that given in (58), and contraction 1:2:3:4 provides us with the term
![]() (60)
(60)
The sum of the Schrödinger terms belonging to ΔE5 is a sum of terms entering (38), (41)-(43), (45), (48)-(51), (55), (58), (59) and (60). The total number of these terms is![]() .
.
A compact presentation of the perturbation energies ΔEN from N = 1 to N = 5 is given in Table 2.
7. Examples of the Calculation of ΔEN: N = 6 and N = 7
The calculation for N = 6 is based on partitions of the number
![]() (61)
(61)
which are next joined with a single number 1 representing the beginning-end point on the diagram; see Table 3. Table 3 gives also the products of Si where i are the numbers entering partitions of 5 in (61). In this way the perturbation components of the energy term ΔE6 listed below are obtained the first of which is:
![]() (62)
(62)
This term is coming from the uncontracted loop (main loop) of time represented by the first partition entering Table 3. The next terms
![]() (63)
(63)
![]() (64)
(64)
![]() (65)
(65)
![]() (66)
(66)
are coming respectively from the 2nd, 3rd, 4th and 5th partition given in Table 3 (contractions 4:5, 3:4, 2:3, and 1:2).
The terms
![]() (67)
(67)
![]() (68)
(68)
![]() (69)
(69)
are coming respectively from the 6th, 7th and 8th partition given in Table 3 (contractions![]() ,
, ![]()
![]() , and
, and![]() ).
).
The six terms
![]() (70)
(70)
![]() (71)
(71)
![]() (72)
(72)
come from the 9th, 10th and 11th partition in Table 3 (contractions 3:5 and 3:4:5 for partition 9, contractions 2:4 and 2:3:4 for partition 10, contractions 1:3 and 1:2:3 for partition 11). The following four terms
![]() (73)
(73)
![]() (74)
(74)
are coming from partitions 12 and 13 in Table 3 [contractions 1:2 and 3:5 for the first term in (73), contractions 1:2 and 3:4:5 for the second term in (73), contractions 1:3 and 4:5 for the first term in (74), contractions 1:2:3 and 4:5 for the second term in (74)].
The next five terms entering ΔE6 are represented by the formulae given below, the first expression is
![]() (75)
(75)
This term is obtained, in the first step, from contraction 2:5. Such contraction implies in fact two terms. The first one is coming from the uncontracted loop 2:5, the other is coming from supplementary contraction 3:4 giving a combined contraction ![]() on that loop. Contributions coming from both situations combine into two terms representing the perturbation energy ΔE3. The other three terms are
on that loop. Contributions coming from both situations combine into two terms representing the perturbation energy ΔE3. The other three terms are
![]() (76)
(76)
coming from contraction 2:3:5,
![]() (77)
(77)
coming from contraction 2:4:5,
![]() (78)
(78)
coming from contraction 2:3:4:5.
A similar set of five perturbation terms is given, in the first step, by contraction 1:4 (which represents two terms), next by contractions 1:3:4, 1:2:4 and 1:2:3:4. The terms are
![]() (79)
(79)
![]() (80)
(80)
![]() (81)
(81)
![]() (82)
(82)
Because of property of symmetry of the bracket terms we have equal values for (75) and (79), a similar equality for (76), (77), (80) and (81), and also for (78) and (82).
The remainder of 14 perturbation terms belonging to N = 6 is given by partition containing (5) (see Table 3). In the first step the terms are given by contraction
![]() (83)
(83)
which represents 5 terms because
![]() (84)
(84)
These terms combine into a single term containing the energy factor equal to ΔE4:
![]() (85)
(85)
Further terms are
![]() (86)
(86)
![]() (87)
(87)
![]() (88)
(88)
given respectively by contractions 1:2:5, 1:3:5 and 1:4:5. The contractions 1:2:5 and 1:4:5 involve the loops of time characteristic for ΔE3, so each of these contractions represents two perturbation terms. In effect (86)-(88) give five terms. The last four terms for ΔE6 are
![]() (89)
(89)
![]() (90)
(90)
![]() (91)
(91)
![]() (92)
(92)
The contractions for the above terms are respectively
![]() (93)
(93)
The diagrams for the perturbation terms of N = 6 are listed explicitly in [7] .
For the calculations of ΔE7 the suitable partitions concern
![]() (94)
(94)
These partitions together with products of Si, where i are the numbers entering partitions, are presented in Table 4. The first perturbation term is coming from the diagram having no contractions. Therefore it is represented by a single (main) loop of time:
![]() (95)
(95)
The next terms and contractions leading to them are
![]() (96)
(96)
![]() (97)
(97)
![]() (98)
(98)
![]() (99)
(99)
![]() (100)
(100)
The above terms come from the 2nd to 6th of partitions given in Table 3. The next six partitions (from 7th to 12th) give
![]() (101)
(101)
![]() (102)
(102)
![]() (103)
(103)
![]() (104)
(104)
![]() (105)
(105)
![]() (106)
(106)
Next come partitions each providing two diagrams representing two energy terms. These partitions are having a single (3) as their component; see Table 4. The terms are
![]() (107)
(107)
(contractions 4:6 and 4:5:6),
![]() (108)
(108)
(contractions 3:5 and 3:4:5),
![]() (109)
(109)
(contractions 2:4 and 2:3:4),
![]() (110)
(110)
(contractions 1:3 and 1:2:3).
The next terms are coming from diagrams belonging to partitions in Table 3 having single (2) and (3). The terms are:
![]() (111)
(111)
(contractions ![]() and
and![]() ),
),
![]() (112)
(112)
(contractions ![]() and
and![]() ),
),
![]() (113)
(113)
(contractions ![]() and
and![]() ),
),
![]() (114)
(114)
(contractions ![]() and
and![]() ),
),
![]() (115)
(115)
(contractions ![]() and
and![]() ),
),
![]() (116)
(116)
(contractions ![]() and
and![]() ).
).
The next partition of Table 4 contains three components of (2). This gives a single energy term
![]() (117)
(117)
which corresponds to contractions![]() .
.
On the other hand a partition in Table 4 which has two (3) as its components provides us with following four perturbation terms:
![]() (118)
(118)
(contractions 1:3 and 4:6),
![]() (119)
(119)
(contractions 1:3 and 4:5:6),
![]() (120)
(120)
(contractions 1:2:3 and 4:6),
![]() (121)
(121)
(contractions 1:2:3 and 4:5:6).
The next step is given by three partitions having single component (4). If (4) means the points 3, 4, 5, 6 chosen on the loop of time we obtain
![]() (122)
(122)
because 6 − 3 = 3. Since S3 = 2 there are two perturbation terms present in (122) given by contractions 3:6 alone and 3:6 combined with 4:5. But S4 = 5, so still ![]() terms are lacking for the chosen partition. These terms are
terms are lacking for the chosen partition. These terms are
![]() (123)
(123)
![]() (124)
(124)
![]() (125)
(125)
They correspond respectively to contractions 3:4:6, 3:5:6 and 3:4:5:6.
Another choices of four successive time points in a partition concern 2, 3, 4, 5 and 1, 2, 3, 4. The first of these choices provides us with the five terms
![]() (126)
(126)
![]() (127)
(127)
![]() (128)
(128)
![]() (129)
(129)
corresponding to contractions 2:5, 2:3:5, 2:4:5 and 2:3:4:5. The second of choices mentioned above formula (126) gives another five terms:
![]() (130)
(130)
![]() (131)
(131)
![]() (132)
(132)
![]() (133)
(133)
The contractions for these terms are 1:4, 1:2:4, 1:3:4 and 1:2:3:4.
Each of two partitions having both (2) and (4) gives also five perturbation terms. The set of terms obtained from one of these partitions is
![]() (134)
(134)
![]() (135)
(135)
![]() (136)
(136)
![]() (137)
(137)
These terms correspond respectively to contractions![]() ,
, ![]() ,
, ![]() and
and ![]()
![]() .
.
The other partition having (2) and (4) gives:
![]() (138)
(138)
![]() (139)
(139)
![]() (140)
(140)
![]() (141)
(141)
in reference to contractions![]() ,
, ![]() ,
, ![]() and
and![]() .
.
The number remaining of terms which belong to N = 7 beyond of 62 terms quoted above is
![]() (142)
(142)
They can be provided by two partitions of Table 4 having (5), these partitions represent ![]() terms, and partition having (6) involves 42 terms. A partition having (5) provides us, in the first step, with 5 terms which are combined together into one term equal to
terms, and partition having (6) involves 42 terms. A partition having (5) provides us, in the first step, with 5 terms which are combined together into one term equal to
![]() (143)
(143)
This expression is due to contraction 2:6 which gives a loop of time characteristic for ΔE4 which contains S4 = 5 terms. The other five terms are represented by:
![]() (144)
(144)
![]() (145)
(145)
![]() (146)
(146)
They are given by contractions 2:3:6, 2:4:6 and 2:5:6. Two of these contractions give two ΔE3 terms and any of these terms combines two perturbation terms.
The next terms involving points 2 and 6 in contractions are:
![]() (147)
(147)
![]() (148)
(148)
![]() (149)
(149)
![]() (150)
(150)
The contractions corresponding to the above four terms are 2:3:4:6, 2:3:5:6, 2:4:5:6 and 2:3:4:5:6. In total 14 terms are obtained from (143)-(150).
Other 14 terms can be obtained from the second partition in Table 4 containing the component of (5). These terms differ from those in (143)-(150) only by position of the exponent at P in the bracket terms:
![]() (151)
(151)
![]() (152)
(152)
![]() (153)
(153)
![]() (154)
(154)
![]() (155)
(155)
![]() (156)
(156)
![]() (157)
(157)
![]() (158)
(158)
The contractions leading to the above terms are similar to those applied before in (143)-(150). A difference is due to the fact that now contractions involve the points from 1 to 5 on the scale instead of points from to 2 to 6 applied before.
A part of 42 diagrams (and perturbation terms) coming from a single partition in Table 4 having (6) are 14 in their number and are due to contaction 1:6. These 14 terms can be combined in a single term
![]() (159)
(159)
since the loop of time given by 1:6 is corresponding to ΔE5 and S5 = 14. In the next step other perturbation terms involving points 1 and 6 in their contractions are:
![]() (160)
(160)
![]() (161)
(161)
![]() (162)
(162)
![]() (163)
(163)
The terms in (160)-(163) are due to contractions 1:2:6, 1:3:6, 1:4:6 and 1:5:6. The number of terms combined in the last four formulae is an effect of S4 = 5 and S3 = 2. In total (160)-(163) provide us with another 14 perturbation terms.
The last 14 terms coming from the partition having (6) are given, in the first step, by the formulae
![]() (164)
(164)
![]() (165)
(165)
![]() (166)
(166)
![]() (167)
(167)
![]() (168)
(168)
![]() (169)
(169)
The above six formulae are given, respectively, by contractions
![]() (170)
(170)
which represent nine perturbation terms because ΔE3 means the presence of two terms. The five remaining terms are:
![]() (171)
(171)
![]() (172)
(172)
![]() (173)
(173)
![]() (174)
(174)
![]() (175)
(175)
The above terms are coming from contractions 1:2:3:4:6, 1:2:3:5:6, 1:2:4:5:6, 1:3:4:5:6 and 1:2:3:4:5:6.
8. General Characteristics of Diagrams and Corresponding Energy Terms
The general aim of the present and former papers [7] -[10] was to make the Schrödinger formalism―especially complicated at large perturbation orders N―to be as simple as possible. In the first step this is done with the aid of a circular scale of time which defines the development of the perturbation process. The scale―specified for each perturbation term or a set of such terms―is represented by a superposition of loops, one of these loops is necessarily the main loop for a given diagram. Such loop has the beginning-end point of time important for the whole diagram. Beyond of the main loop there exists for each N > 2 also a side loop, or a set of side loops.
A principal difference between the main loop and a side loop is that the beginning-end point present on the main loop cannot be submitted to contractions, whereas the beginning-end point on a side loop can be submitted to such contraction operation with other points present on that loop, on condition the number of these points is large enough, i.e. it is larger than zero.
A special aim of the present paper was to introduce, as a separate step, a partition procedure to the numbers
![]() (176)
(176)
which are the perturbation orders of the Schrödinger theory decreased by one.
The joined effect of the scale application and partition operation of N − 1 points present on it provides us with a set of the required SN energy terms in a relatively simple way. In practice the number of the terms necessary to calculate can be smaller than SN because the formalism allows us in general to combine several terms of the SN set into the energy terms belonging to orders lower than N. This seems to be advantageous because in fact the aim of the calculation is to obtain the ΔEN and not necessarily their separate components.
In general the contributions to any ΔEN having N > 2 are given by the products of a term provided by the main loop of time and a term, or terms, provided by the side loops. This second kind of terms can be regularly represented by the sets of the Schrödinger perturbation terms for energy equal to ΔEN' for which
![]() (177)
(177)
The largest of N' present in (177) is
![]() (178)
(178)
the smallest is regularly
![]() (179)
(179)
Any partition of N − 1 gives the partitions number equal to
![]() (180)
(180)
Because of a combination of the Schrödinger perurbation terms into ![]() where
where
![]() (181)
(181)
done in course of the calculation of ΔEN, we have for N > 3
![]() (182)
(182)
It should be noted that among the terms entering the set of WN or SN there exists for any N > 1 only one term which is represented by the partition
![]() (183)
(183)
A diagram corresponding to such term has no contractions and is represented only by the main loop of time.
The contributions due to the presence of the side loops are given by a single term
![]() (184)
(184)
if only a single side loop is present, by the product of two terms
![]() (185)
(185)
in case of the presence of two side loops, etc, because any side loop gives a separate contribution to the product of energy terms
![]() (186)
(186)
representing a contribution obtained from a set of many side loops;![]() .
.
On the other hand, the contribution to the energy term coming from the main loop of time is represented by the formula
![]() (187)
(187)
Here symbol V is a single matrix element calculated for the perturbation potential V in (39) whereas ![]()
![]() are symbols of the reciprocal expression of the energy difference between the unperturbed energy states
are symbols of the reciprocal expression of the energy difference between the unperturbed energy states
![]() (188)
(188)
etc. The summation symbols run over the unperturbed states different than n; see (36).
If BV is the number of times with which V enters the bracket term in (187), the exponents of the P’s entering (187) and the number ![]() of the side loops should satisfy the relation
of the side loops should satisfy the relation
![]() (189)
(189)
For many brackets of the kind given in (187) there can exist a mirror symmetry concerning the exponents of the P’s, for example we can have a pattern of exponents
![]() (190)
(190)
When (190) applies, there holds also the equality
![]() (191)
(191)
because of the property of the integration process with which the terms of the kind of (191) are calculated; see [9] .
The symmetry of the kind given in (191) provides us with a further reduction of the number of the SN terms necessary to calculation of ΔEN for a given N. Effects of such reduction are evident especially for large N.
9. Summary and Discussion
The paper does, in its first step, an overview of the scales of time in which a classical scale of time characteristic for the everyday life and applied also in physics is compared with some other possible scales.
In the next step it has been demonstrated that a treatment of the perturbation problem in quantum mechanics requires a scale of time which is much different from the well-established scale of classical physics applied also in the Feynman approach to the quantum-mechanical problems. A new scale of time is typically circular in its character and its effect is compared with a former scale in course of solving the Schrödinger perturbation problem of a nondegenerate quantum-mechanical state.
For a large perturbation order N the Feynman approach gives a dramatic inflation of the number of diagrams and their energy terms which are necessary to be first calculated and next combined in the Schrödinger perturbation terms for energy. For example, to calculate the perturbation energy of order N = 20 we should consider the number of
![]() (192)
(192)
of such terms. On the other hand, in the present formalism the number of terms which should be calculated in order to obtain ΔE20 does not exceed
![]() (193)
(193)
The terms WN, which come from the main loop of time, are given solely in the form of the bracket expressions (187) and represent contributions of the main loops of time present on the diagrams obtained on the circular scale; the contributions from the side loops are products of ΔEN' where![]() .
.
The number of different bracket expressions for the perturbation order N occurs to be equal to the number of partitions of the number N − 1 and is given in (180) for each N > 2. In fact the number of terms necessary to calculate WN for large N can be reduced to about a half of WN because of symmetry properties entering the bracket terms (187).
A full number of SN perturbation terms represented by the formula (11) can be attained also on the basis of partitions of the number N − 1; see Section 4 and Table 3 and Table 4.
A rather fundamental question may arise to what extent the time scale which fits the Schrödinger perturbation formalism can be checked in course of a physical process or with the aid of the measured data. A general difficulty is that the quantum processes are of an extremely short duration and as such become almost inaccessible in their time details. Another problem is that ΔE, being an energy aiming to a stationary (perturbed) quantum state, has no dependence on time at all.
A general look on the space-time relations in quantum mechanics has been done in [12] . But a special kind of the time dependence has been introduced to stationary states by considering their evolution according to the time-dependent Schrödinger equation together with an averaging process concerning some set of observables whereas another set is assumed to be fixed [13] . Since partition of the observables in two sets can be assumed to change with time, we obtain a kind of history of a stationary state defined by the state function Ψ. This formalism has been developed by Omnes [14] and next by Gell-Mann and Hartle [15] but seems to be too complicated for its use in the present theory.
In fact a production of ΔE in a system should occupy some interval of time Δt. An insight into dependence between ΔE and Δt can be obtained from the uncertainty relation which has to be satisfied by these quantities. This is (see [16] -[18] )
![]() (194)
(194)
If ΔE can be limited to only one of its components, say
![]() (195)
(195)
a limit for the length of the interval Δt necessary to produce the energy ΔE can be obtained for example from a study of the diamagnetism of an atom having the orbital angular momentum L and spin S equal to zero [19] . Let the atom has spherical symmetry and its ΔE1 is the energy change due to the atom diamagnetism in the magnetic field of strength H, so [19]
![]() (196)
(196)
the ![]() are the values of the electron distances from the atomic nucleus. Let the sum of the
are the values of the electron distances from the atomic nucleus. Let the sum of the ![]() averaged for all directions be equal to
averaged for all directions be equal to
![]() (197)
(197)
Assuming the magnetic field of strength H = 1 oersted, we obtain from (196) the relation
![]() (198)
(198)
from which the time interval necessary to be occupied by the loop representing N = 1 becomes [see (194) and (195)]
![]() (199)
(199)
This result can be compared with that obtained for the same interval ΔE from the Heisenberg uncertainty relation
![]() (200)
(200)
In this case we obtain because of
![]() (201)
(201)
the interval
![]() (202)
(202)
which physically seems to be a highly unrealistic result.