Modified Maximum Likelihood Estimation in Autoregressive Processes with Generalized Exponential Innovations ()
1. Introduction
The common model for a stationary time series is the stationary and invertible autoregressive model of order  where the usual assumption is that the innovations
where the usual assumption is that the innovations 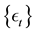 are identically and independently distributed (IID) according to a Gaussian distribution with zero mean and variance
are identically and independently distributed (IID) according to a Gaussian distribution with zero mean and variance .
.
Recent and past literatures agree in that the assumption of Gaussianity is a way too restrictive in order to deal with applications (see [1] and [2] with the references therein). On the other hand, [3] assumed 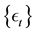 has a Laplace distribution and computes the maximum likelihood (ML) estimators by using iterative methods. [2] have used the modified likelihood function proposed by [4] which is based on censored normal samples [5] and have studied the robustness properties of the resulting estimators. In this context, [6] generated non-Gaussian distributions through transformations of a Gaussian variate.
has a Laplace distribution and computes the maximum likelihood (ML) estimators by using iterative methods. [2] have used the modified likelihood function proposed by [4] which is based on censored normal samples [5] and have studied the robustness properties of the resulting estimators. In this context, [6] generated non-Gaussian distributions through transformations of a Gaussian variate.
[7] considered the Huber M-estimation, which is valid under heavy-tailed symmetric distributions, and uses different forms of contaminated Gaussian to compute the influence functionals (IF) of parameter estimates and gross-error sensitivity for the IF. In this context, [8] and [9] have studied the rate of convergence of the least squares (LS) estimators. It may be noted that M-estimation is not valid for skewed distributions, and has the problem of inefficient estimates for short-tailed symmetric distributions; this has been widely shown by [1] in the classical framework of IID observations.
[10] obtained approximations to some likelihood functions in the context of state space models as considered by [11] . Besides, [12] considered an asymmetric Laplace distribution for the innovations of an autoregressive and moving average model and of a generalized autoregressive conditional heteroscedastic model.
The main proposal of our paper is based on the use of modified likelihood as introduced by [13] [14] and [15] under the framework of IID observations, in order to estimate the parameters in the context of simple linear regression with stationary and invertible autoregressive errors of order one with innovations represented by Generalized Exponential distribution; for more details on these distributions the reader refers to [16] . This method is notorious for giving asymptotically fully efficient estimators (for example, see [17] -[20] ).
The outline of the paper is as follows. In Section 2 we define the regression linear model with autoregressive errors, where the underlying distribution of the innovations is a Generalized Exponential distribution. In Section 3 we propose the MML estimators as a powerful methodology to deal with ML estimators which are intractable in the case of a Generalized Exponential distribution. In Section 4 we study the asymptotic properties of the proposed estimators. The main advantages of the proposed estimators are discussed via simulation studies in Section 5. Finally discussions and observations appear in Section 6 of the proposed model and the specific numerical results, attaching an Appendix which displays the details of asymptotic results.
2. The Model
We denote 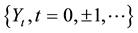 a time series and the following model
a time series and the following model
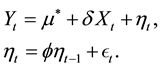 (1)
(1)
where Xt is the value of a fixed design variable X at time t, 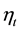 is the error, assumed to be modeled through a non-Gaussian stationary autoregressive model,
is the error, assumed to be modeled through a non-Gaussian stationary autoregressive model,  is a constant,
is a constant, 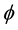 is the autoregressive coefficient, with
is the autoregressive coefficient, with , and
, and 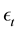 is the innovation, distributed according to a Generalized Exponential distribution (GEd), given by
is the innovation, distributed according to a Generalized Exponential distribution (GEd), given by
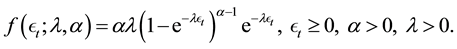 (2)
(2)
The corresponding cumulative distribution function is given by
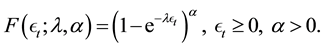 (3)
(3)
Notably, 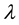 and
and 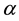 play, respectively, the role of scale and shape parameters. The
play, respectively, the role of scale and shape parameters. The  has a similar form to the Gamma and Weibull distributions. See the survey in [21] for some recent developments on GEd, distributions.
has a similar form to the Gamma and Weibull distributions. See the survey in [21] for some recent developments on GEd, distributions.
3. Modified Maximum Likelihood Estimators
The model in Equation (1) can be written as
![]() (4)
(4)
or
![]() (5)
(5)
whit![]() ,
, ![]() is the autoregressive polynomial, and
is the autoregressive polynomial, and ![]() is the backward shift operator. Conditional on
is the backward shift operator. Conditional on![]() , the likelihood function for the parameter vector
, the likelihood function for the parameter vector ![]() in model (4) is given by
in model (4) is given by
![]() (6)
(6)
where![]() , with
, with ![]() or
or![]() ,
, ![]() given by
given by
![]() (7)
(7)
The log-likelihood is given by
![]() (8)
(8)
For convenience we introduce at this point the following reparameterization: ![]() and
and![]() . Then the density function of
. Then the density function of ![]() is given by
is given by
![]() (9)
(9)
where ![]() and
and![]() . Its cumulative distribution function is
. Its cumulative distribution function is
![]() (10)
(10)
Now![]() , and note that
, and note that ![]() is the standardized member of the GE family. The log-likelihood for the parameter vector
is the standardized member of the GE family. The log-likelihood for the parameter vector ![]() then becomes
then becomes
![]() (11)
(11)
Also note that if we consider the parameter ![]() as fixed, then the log-likelihood for the reduced parameter vector,
as fixed, then the log-likelihood for the reduced parameter vector, ![]() , is proportional to
, is proportional to
![]() (12)
(12)
For notational simplicity, let us write![]() . Then, direct inspection shows that first derivatives of the log-likelihood function with respect to
. Then, direct inspection shows that first derivatives of the log-likelihood function with respect to ![]() and
and ![]() can be written as:
can be written as:
![]() (13)
(13)
The likelihood equations are expressions in terms of intractable functions![]() , which lead no explicit solutions, using as alternative numeric iterative methods for get the solutions.
, which lead no explicit solutions, using as alternative numeric iterative methods for get the solutions.
In order to obtain efficient closed form estimators, we consider Tiku’s method of modified likelihood estimation, which is by now well established, see [22] (Chapter 6). For given values of![]() ,
, ![]() ,
, ![]() , and
, and![]() , let
, let ![]() be the order statistics of
be the order statistics of![]() . Let
. Let![]() , with
, with![]() , be the expected values of the standardized order statistics.
, be the expected values of the standardized order statistics.
A standard Taylor expansion of ![]() around
around ![]() up to first order allows us to obtain
up to first order allows us to obtain
![]() (14)
(14)
where ![]() and
and![]() . A closed form expression for
. A closed form expression for ![]() has been calculated by [23] , namely
has been calculated by [23] , namely
![]() (15)
(15)
where ![]() is the Digamma function. However, for large n, and using the Delta Method, we have the well-known approximation for
is the Digamma function. However, for large n, and using the Delta Method, we have the well-known approximation for ![]() for sufficiently large n,
for sufficiently large n, ![]() , with
, with
![]() (16)
(16)
where ![]() is the inverse of the cumulative distribution function of
is the inverse of the cumulative distribution function of![]() , see for instance [22] . Since
, see for instance [22] . Since ![]() is locally linear ([14] [15] ), under some very general regularity conditions,
is locally linear ([14] [15] ), under some very general regularity conditions, ![]() converges to
converges to ![]() as the sample size becomes large, in a small interval not containing the zero value.
as the sample size becomes large, in a small interval not containing the zero value.
Plugging (14) into (13), we obtain the approximated derivative of the log-likelihood function for![]() , which can be written as
, which can be written as
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
The zeros of the above system of equations are the MML estimators of![]() . For the sake of clarity, let
. For the sake of clarity, let
![]() , where
, where ![]() and
and ![]() are the concomitants, the associate values of
are the concomitants, the associate values of ![]() and
and ![]() for
for![]() , of
, of
![]() . Then, from Equations (17) and (18) we get
. Then, from Equations (17) and (18) we get
![]()
Then, from the Equations (17) and (19) we get
![]()
Defining the n-dimensional vectors, ![]() ,
, ![]() ,
, ![]() , and
, and
![]() , the identities above lead to the following expressions for the MML estimators of
, the identities above lead to the following expressions for the MML estimators of![]() :
:
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
where
![]()
and
![]()
Furthermore, note that setting the expression for ![]() in (13) to zero and solving for b, while substituting
in (13) to zero and solving for b, while substituting ![]() gives
gives
![]() (24)
(24)
We note that the coefficients![]() ’s are positive. It is expected if the
’s are positive. It is expected if the![]() ’s have positive values, then
’s have positive values, then![]() ’s are all negatives, so
’s are all negatives, so ![]() is negative. And if d is negative, no complex roots occur for
is negative. And if d is negative, no complex roots occur for![]() .
.
Moreover![]() , and
, and![]() , resulting as an estimator for
, resulting as an estimator for![]() ,
,![]() . We
. We
observe that these estimates involve the ![]() parameter.
parameter.
These facts suggest that it is possible to obtain MML estimators of ![]() by using the following iterative procedure. As a starting point, consider the LS estimator for
by using the following iterative procedure. As a starting point, consider the LS estimator for![]() , with
, with![]() , which is given by
, which is given by
![]() (25)
(25)
where
![]() (26)
(26)
![]() (27)
(27)
![]() (28)
(28)
We suggest the following routine for the numerical computation of the MML estimator. Initialize with ![]() and
and ![]() (an exponential distribution).
(an exponential distribution).
Step 0. Set ![]() the LSE from (25).
the LSE from (25).
Step 1. Get ![]() from (21) using
from (21) using![]() , and
, and ![]() from (22) using
from (22) using![]() . Update
. Update ![]() with (23);
with (23); ![]() with (24).
with (24).
Step 2. Evaluate the expressions (15)-(17) in ![]() with the initial estimated values
with the initial estimated values ![]()
Step 3. Get from (7) the initial estimates for the![]() . Sort the set
. Sort the set ![]() saving the corresponding concomitants values of
saving the corresponding concomitants values of ![]() say
say![]() .
.
Step 4. With the values of Step 3, get ![]() from (23) and get
from (23) and get ![]() from (24), to obtain the complete initial values vector
from (24), to obtain the complete initial values vector![]() .
.
Step i. Get ![]() from (21) using
from (21) using![]() , and
, and ![]() from (22) using
from (22) using![]() . Update
. Update ![]() with (23),
with (23), ![]() with (24).
with (24).
The steps are repeated until convergence is achieved.
Remark. The stopping criteria is given by
![]()
4. Asymptotic Equivalence and Efficiency
The asymptotic equivalence of MML and ML estimators is based on the fact that ![]() converges to zero as n tends to infinity. Thus, following [17] we have that the differences,
converges to zero as n tends to infinity. Thus, following [17] we have that the differences, ![]() and
and ![]() tend to zero asymptotically. Therefore, the MML and ML estimators are asymptotically equivalent.
tend to zero asymptotically. Therefore, the MML and ML estimators are asymptotically equivalent.
On the other hand, if we know the values of ![]() and
and![]() , asymptotically, the MML estimators
, asymptotically, the MML estimators ![]() and
and
![]() are unbiased for
are unbiased for ![]() and
and![]() . Namely, let
. Namely, let ![]() be the parameter vector and by applying the
be the parameter vector and by applying the
standard Taylor expansion in a neighborhood of ![]() we have (see [24] )
we have (see [24] )
![]()
Using the results (5.7.5), p. 115 of [25] and Lemma 1 in the Appendix, we show that ![]() for large n. The unbiasedness property of
for large n. The unbiasedness property of ![]() is analogous to the previous case.
is analogous to the previous case.
Furthermore, if we know the values of ![]() and
and![]() , the MML estimators
, the MML estimators ![]() and
and ![]() are unbiased and normally distributed with variance-covariance matrix
are unbiased and normally distributed with variance-covariance matrix
![]() (29)
(29)
knowledge of the values of ![]() and
and![]() . Observe that
. Observe that
![]()
with![]() ,
, ![]() and
and![]() . Thus, we have (29) for the asymptotic variance- covariance matrix of
. Thus, we have (29) for the asymptotic variance- covariance matrix of![]() .
.
The asymptotic behavior of variance for ![]() (say
(say![]() ) and
) and ![]() (say
(say![]() ) can be deduced from the arguments in [26] . We can thus show that
) can be deduced from the arguments in [26] . We can thus show that![]() , where
, where
![]()
Analogously, we have![]() , where
, where
![]()
where ![]() is jth derivative of the moment generating function of
is jth derivative of the moment generating function of![]() ,
, ![]() is the rth non-central moment of
is the rth non-central moment of ![]() given by the Lemma 2 of the Appendix for
given by the Lemma 2 of the Appendix for![]() .
.
5. Simulation Study
In order to have some indications of the robustness aspects of the MML estimates of![]() ,
, ![]() ,
, ![]() and
and ![]() against LSE estimates, we performed a small numerical study similar to the one presented by [26] for the generalized logistic model. We consider the following AR(1) Generalized Exponential model:
against LSE estimates, we performed a small numerical study similar to the one presented by [26] for the generalized logistic model. We consider the following AR(1) Generalized Exponential model:
![]() (30)
(30)
where![]() . Additionally, our simulation study considers different scenarios, sketched as follows:
. Additionally, our simulation study considers different scenarios, sketched as follows:
1) ![]()
![]()
![]() and
and ![]()
2) ![]()
![]()
![]() and
and ![]()
3) ![]()
![]()
![]() and
and ![]()
4) ![]()
![]()
![]() and
and ![]()
5) ![]()
![]()
![]() and
and ![]()
Without loss of generality, we have considered the parameter b as a constant value given by b = −1 and −2. The summaries of Monte Carlo study for![]() ,
, ![]() ,
, ![]() and
and![]() , come from the four measures, the mean, 100 × (Bias)2, variance and mean squared error (MSE) for both the LS and the MML estimators. Finally, we use sample size n = 100 and 10,000 replications. Table 1 displays the results from the simulations with the biases, variance and MSE of the parameters estimates. The results suggest that the MML estimators are considerably more efficient than the LS estimators for all parameters.
, come from the four measures, the mean, 100 × (Bias)2, variance and mean squared error (MSE) for both the LS and the MML estimators. Finally, we use sample size n = 100 and 10,000 replications. Table 1 displays the results from the simulations with the biases, variance and MSE of the parameters estimates. The results suggest that the MML estimators are considerably more efficient than the LS estimators for all parameters.
6. Conclusion
In this paper, we have studied a regression linear model with first-order autoregressive errors belonging to a class of asymmetric distributions; more specifically the underlying distribution for the innovations is a Generalized Exponential distribution. We have developed a complete asymptotic theory for the MML estimators in these models. In addition, we have shown that the MML estimators are robust and efficient, as depicted by the numerical study presented in Section 5 for the AR(1) GE model. We thus claim that the MML estimator is a very good alternative to estimate autoregressive models with asymmetric innovations (see [26] and [27] , among others as example). The R codes may be obtained from the authors upon request in order to analyze such models.
Acknowledgements
The first author would like to thank for the support from DIUC 213.014.022-1.0, established by the Universidad de Concepción. The second author gratefully acknowledges the financial support from ECOS-CONICYT C10E03, established by the Chilean Government and DIUC 213.014.021-1.0 from the Universidad de Concepción and the third author was supported by Fodecyt grant 1130647.
Appendix
Lemma 1. Let![]() ,
, ![]() ,
, ![]() and p,
and p, ![]() such that
such that ![]() and
and![]() , then
, then
![]()
where ![]() is jth derivative of the moment generating function of
is jth derivative of the moment generating function of![]() .
.
Proof
![]()
Lemma 2. For the process ![]() defined as a stationary autoregressive model,
defined as a stationary autoregressive model, ![]() ,
, ![]() is the autoregressive coefficient, with
is the autoregressive coefficient, with![]() , and
, and ![]() is distributed according to a GEd. The first and second moment are given by
is distributed according to a GEd. The first and second moment are given by
![]()
Proof is deduced by using the moment generating function of ![]()
![]() (31)
(31)
(see [21]). Moreover, for the![]() , we used
, we used
![]()
and for![]() , we used
, we used
![]()