1. Introduction
An important fact has recently started to occur in the context of business surveys. More and more official national business registers in the world have been georeferenced in their entirety. That is, they record the precise spatial coordinates (in terms of longitude and latitude) of each single business unit. For example, to name a few, one should mention the US Census Bureau’s Longitudinal Business Database (LBD), the OFS Suisse Geo Stat STATENT and the Italian Statistical Archive of Active Enterprises (ASIA). This detailed kind of spatial information has never been exploited in establishment surveys in order to select spatially balanced samples of firms.
Literature on sampling, since the seminal paper by Arbia [1] , has recognized that spatial heterogeneity in the population data and spatial autocorrelation of the target variables, if not properly taken into account, may negatively affect the efficiency and precision of the samples estimates. More recently, a stream of literature proposed different sampling procedures which incorporate the spatial location of units into the design and assure that the selected samples are spatially balanced, which are well spread over the spatial population. In the context of environmental data, it has also been proved that spatially balanced samples lead to more efficient estimates than samples selected without considering the spatial aspects.
It is argued that, even in the context of establishment surveys, the feature of spatial dependence is relevant as firms located near in space are more similar than those located far apart. Therefore, it is reasonably expected that spatial sampling designs should perform better than the non-spatial ones, even when conducting business surveys. In this paper, it is aimed for verifying this hypothesis by means of simulations. In particular, referring to an observed population of business units, the purpose is to measure the performance of spatial sampling designs for firm data. Furthermore, it is also aimed for individuating which is the most proper spatial sampling design, amongst those proposed in the literature, to conduct business surveys. In particular, the population of firms has been defined from the Italian ASIA archive in which the target variable is the firm’s sales and the goal is to estimate the population total. The different spatial sampling designs under comparison will be the Spatially Correlated Poisson Sampling method (SCPS) by Grafström [2] , the Local Pivotal methods (LPM1 and LPM2) by Grafström et al. [3] , the Balanced Sampling (BS) by Deville and Tillé [4] and the Doubly Balanced Spatial Sampling (DBSS) by Grafström and Tillé [5] . For all designs, the Horvitz-Thompson estimator of the population total will be used both with equal and unequal inclusion probabilities proportional to the number of employees of business units. The performance of the designs will be evaluated in terms of efficiency of the HT estimator.
The structure of the paper is the following. In Section 2, the spatial sampling designs that have been tested on the firm data have been briefly introduced. Section 3 contains the results of the simulation study. Finally, Section 4 contains some conclusions and directions for further studies in the field.
2. Spatial Sampling Designs
In the last three decades, spatial sampling field has been involved in a flourishing of proposals to incorporate spatial information in sampling designs. For example, very ample is literature on the exclusion of contiguous units in selecting samples (Hedayat et al., [6] and [7] ; Wright and Stufken, [8] ). Moreover, another field of research has been concentrating his effort in study how is possible to guide selection of samples giving geographic coordinates as part of available information on the study population. The most important turning point is definitively attributable to Stevens and Olsen [9] , which proposed an innovative method to select spatial samples.
The Generalized Random-Tessellation Stratified method (GRTS), proposed by Stevens and Olsen [9] , essentially consists on assigning to sampling units an order according to a recursive hierarchical randomization process which preserves the spatial relationships of the sample units. Then, the sampling units are arranged in order and mapped from twoor multi-dimensional space in one-dimensional space, through a quadrant recursive function (Mark, [10] ). The samples are selected in one dimension, using systematic πps sampling and then mapped back in the original twoor multi-dimension, preserving the spatial order. GRTS design ensures that drawn samples are well spread over the space.
The GRTS has been the most utilized probability-based method to give spatially-balanced sample for data on a linear, areal or not contiguous space. GRTS supports sampling with unequal selection probabilities and produces samples that are much more evenly distributed over space than an ordinary unequal probability design. On the other hand, the mapping used in GRTS is not perfect because it does not exclude the possibility that units that are close in distance in the original complex space may be mapped rather far apart in the one dimensional space where the sampling is made.
GRTS has been considered as the first success in spatial sampling. Nevertheless, it could result obsolete in terms of time of computing and implementation if compared with new methods exposed in prosecution. Due to these reasons, it is not implemented in simulation in Section 4.
2.1. Spatially Correlated Poisson Sampling Method
The Spatially Correlated Poisson Sampling method (SCPS), proposed by Grafström [2] , allows to overcome the problems related to the mapping procedure of GRTS. The SCPS is a modification of Correlated Poisson Sampling (CPS): a list sequential method for real time sampling which provides the selection of units with unequal inclusion probabilities (Bondesson and Thorburn, [11] ). The CPS visits units one by one and give to every units a definite inclusion probability. The inclusion probability assigned to each unit is then updated recursively, based on the previous units sampling outcome and in accordance to a specific updating rule characterized by some weights that control how the inclusion probabilities for a unit should be affected by the sampling outcome for the previous units (Bondesson and Thorburn, [11] ).
It is possible to define the vector of inclusion indicators of a random sample 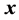 as
as 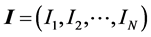 for a population of N units. Given that, the probability function for CPS can be written as
for a population of N units. Given that, the probability function for CPS can be written as
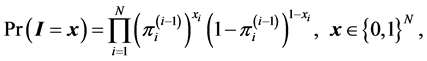
where 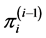 is a function of the first
is a function of the first 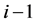 components of the vector
components of the vector 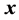 (Grafström, [12] ).
(Grafström, [12] ).
The SCPS design is a modification of CPS, achieved by the introduction of a known distance function 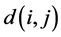 between units in the updating rule. It essentially consists on a set of strategies for choosing weights for CPS. The distance function may be the Euclidean distance or another general distance measure. Grafström [2] proposed maximal weights and Gaussian preliminary weights as strategies for choosing the weights. If the order of units in the list is changed, for maximal weights and Gaussian preliminary weights, the second order inclusion probabilities may be changed. Differently from GRTS, the order of the units is not relevant since the weights depend on distances amongst units. The samples drawn will have sample locations well spread over the population, because the efficiency of the method is independent of the ordering of units. The algorithm visit units (one by one and all at once) and decide whether or not the unit should be sampled. The final intent is to create correlations between the inclusion indicators. In presence of negative correlation, units that are close in distance rarely appear simultaneously in the sample.
between units in the updating rule. It essentially consists on a set of strategies for choosing weights for CPS. The distance function may be the Euclidean distance or another general distance measure. Grafström [2] proposed maximal weights and Gaussian preliminary weights as strategies for choosing the weights. If the order of units in the list is changed, for maximal weights and Gaussian preliminary weights, the second order inclusion probabilities may be changed. Differently from GRTS, the order of the units is not relevant since the weights depend on distances amongst units. The samples drawn will have sample locations well spread over the population, because the efficiency of the method is independent of the ordering of units. The algorithm visit units (one by one and all at once) and decide whether or not the unit should be sampled. The final intent is to create correlations between the inclusion indicators. In presence of negative correlation, units that are close in distance rarely appear simultaneously in the sample.
2.2. Local Pivotal Methods
The Local Pivotal methods (LPM1 and LPM2), proposed by Grafström et al. [3] , are a spatial extension of the Simple Pivotal method (Deville and Tillé, [13] ). LPM methods draw samples considering distances between units and in accordance to the updating rule of the Pivotal method, for two nearby units at each step (see for details, Deville and Tillé, [13] ). To choose the two nearby units i and j, it is possible to choose between LPM1, which is more balanced, and the LPM2, which is less balanced but computationally more feasible.
The LPM1 randomly chooses the first unit i and then the nearest neighbor unit j (if two or more unit have the same distance to i, the method randomly choose between them). The inclusion probabilities are updated according to the updating rule of pivotal method. If j is not the nearest neighbor of i, the method restart from the beginning. When all units have been visited, the method stops. To select a LPM1 sample, the needed expected number of iterations is at most proportional to N3.
The LPM2 works similarly to the LPM1, but the inclusion probabilities are directly updated with the updating rule of the pivotal method. The expected number of iterations needed to select a sample is in this case proportional to N2. The Local Pivotal methods give more spatially balanced samples than GRTS or SCPS for some populations. They imply a smaller variance when a spatial trend exists (Grafström et al., [3] ).
In case of a high amount of available auxiliary information, Local Pivotal methods allow to select samples which are well spread in the space. Moreover, if units near in space have similar values, the estimation could be subjected to an improvement. Similarly, it is possible to assign bigger weights to auxiliary variables which have a strong relationship with the variable of interest.
2.3. Balanced Sampling
Balanced Sampling (BS) is a popular method to select random units from a finite population, taking into account a fixed sample size and stratification. Balanced sampling is very important in the case when the auxiliary variables are correlated with the interest variable. A large family of methods to select balanced samples is available, which comprehends those proposed by Yates [14] , Royall and Herson [15] , Deville et al. [16] , Hedayat and Majumar [17] , Breidt and Chauvet [18] .
However, the Cube method proposed by Deville and Tillé [4] changed completely the perspective of balanced sampling. It is an algorithm to select balanced samples which can use many different auxiliary variables with equal or unequal inclusion probabilities. The Cube method, named after a geometric representation of a sampling design, satisfies predefined inclusion probabilities and drawn samples which are better balanced than those obtained with other balancing methods. It is based on a random transformation of inclusion probabilities vector π to draw a sample s which exactly satisfies the inclusion probabilities and the equation of balancing (see for details, Deville and Tillé, [4] ). The Cube method is composed by two phases: the flight phase and the landing phase. The first one is a random walk which starts on the point of the inclusion probabilities vector and stays within the intersection area between the cube and the constraint subspace. The random walk stops when it arrives in a vertex of the subspace. If the sample is not obtained, then a landing phase is applied where the sample is selected as near as possible to the constraint subspace.
The BS method used in the empirical application of this paper is a particular application of the Cube method, where geographic coordinates have been used as auxiliary variables.
2.4. Doubly Spatial Sampling Method
The Doubly Balanced Spatial Sampling method (DBSS), proposed by Grafström and Tillé [5] , combines the LPM2 (Grafström et al., [3] ) and the Cube methods (Deville and Tillé, [4] ; Tillé, [19] ).
DBSS is a method that succeeds in drawing samples which are balanced on auxiliary variables and well spread in the topographical space. First of all, this method selects a cluster of units through LPM2. In particular, the first unit i is selected randomly with equal inclusion probability and then its nearest unit j is subsequently selected. The mean position of the 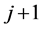 units is computed and then the next unit is selected as the nearest to the mean position. The procedure is repeated as long as the sum of the squares of the distances between cluster units and their mean decreases. When the cluster is selected, DBSS applies the Cube method flight phase on a cluster of units near in distance. Then the sampling outcomes are decided for the units according to the balancing conditions. The second order inclusion probabilities are updated locally. So that they are smaller among nearby units because LPM creates negative correlation between inclusion indicators of nearby units. At the end of the decision process for sampling outcomes, the landing phase of the Cube method is applied.
units is computed and then the next unit is selected as the nearest to the mean position. The procedure is repeated as long as the sum of the squares of the distances between cluster units and their mean decreases. When the cluster is selected, DBSS applies the Cube method flight phase on a cluster of units near in distance. Then the sampling outcomes are decided for the units according to the balancing conditions. The second order inclusion probabilities are updated locally. So that they are smaller among nearby units because LPM creates negative correlation between inclusion indicators of nearby units. At the end of the decision process for sampling outcomes, the landing phase of the Cube method is applied.
The DBSS provides better balanced samples, as those selected by the Cube method. In addition, at each selected unit, the inclusion probability is updated for the remaining units in a decreasing order based on the distance between units. It prevents the selection of units near in distance, giving a sample that is well spread in the space.
To implement the DBSS design a vector of geographic coordinates, to spread the population over the space, and a vector of auxiliary variables for balancing procedure are required. In the simulation study of this paper, geographic coordinates are used both to balance and to spread the population, giving a “dual” spatial connotation to the algorithm.
3. Data
The data used in this paper derive from the ASIA archive. This database, which is managed and updated by the Italian Institute of Statistics (ISTAT), records the entire population of active enterprises operating in the manufacturing and services sectors. It represents the up-to-date reference register for most of the official establishment surveys as it implements the Eurostat’s legislation (art. 1 and 7 of Council Regulation no. 2186/93, [20] ) about the statistical harmonization of the business registers. For each business unit, the database currently contains yearly information about firm code, sector of activity (according to the NACE, which is the Statistical Classification of Economic Activities in the European Community), number of firm’s employees, firm’s sales, legal status (according to the current Italian classification), firm’s birth and death dates and the precise spatial locations (in terms of GMT longitude and latitude coordinates).
4. Simulation Study
In this section the performances, in terms of efficiency and spatial balancing, of the various spatial sampling designs, are assessed in an observed population of business units. The reference population used is a subset of the ASIA archive and it is composed by 822 georeferenced non-specialized retail stores located in the Province of Trento, Italy, in 2009. It is assumed that the goal of sampling is to estimate the population total of firm’s sales. The number of firm’s employees is available as an auxiliary variable.
Figure 1 shows the spatial distribution of stores, where it can be clearly noted that the population units are not evenly distributed in space but they tend to concentrate in three particular areas, corresponding to the three biggest towns of the region. Moreover, Figure 2, which depicts the empirical semivariogram, shows the presence of relevant spatial autocorrelation in the stores’ sales. Denoting the store’s sales with y, for any generic stores i and j that have a function distance d, the empirical semivariogram ordinate is the quantity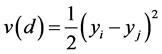 . If the sales of neighboring stores are spatially independent, then
. If the sales of neighboring stores are spatially independent, then 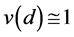 for all
for all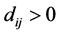 . On the other hand, if the values of sales tend to be similar amongst firms located at a distance d, then
. On the other hand, if the values of sales tend to be similar amongst firms located at a distance d, then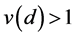 . Figure 2 shows that
. Figure 2 shows that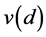 has a peak relevantly greater than 1 at
has a peak relevantly greater than 1 at  meters, indicating that stores’ sales are characterized by
meters, indicating that stores’ sales are characterized by
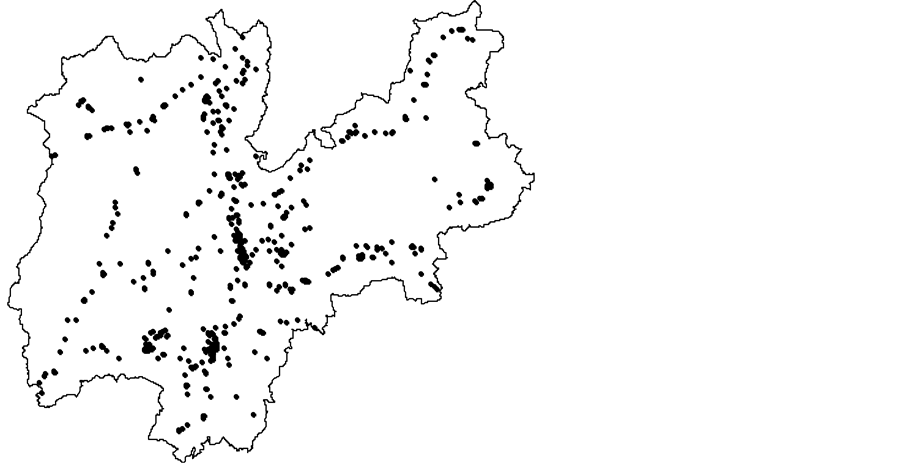
Figure 1. Spatial distribution of population units.

Figure 2. Empirical semivariogram of sales.
a small scale spatial trend which, in turn, suggest that spatial sampling designs may have an important role in producing relatively more precise estimates of population total of sales. Note that the semivariogram ordinates have been averaged in bins of constant width.
In this simulation study, the following sampling designs are compared: LPM1, LPM2, SCPS, BS and DBSS. Six different scenarios are taken into consideration. Indeed, from the population of size N = 822, samples of size n = 50, n = 75 and n = 100 units with both equal and unequal (as proportional to the number of employees) inclusion probabilities have been selected. Observing how the results change with respect to the different scenarios allows assessing, on one hand, the presence of some trends in the fixed sample size and, on the other hand, the ability of sampling designs to exploit auxiliary information.
For all designs, the Horvitz-Thompson estimator has been used (Horvitz and Thompson, [21] ):
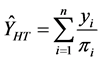
where  and
and 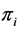 are the values, respectively, of the target variable and inclusion probability of sample unit i.
are the values, respectively, of the target variable and inclusion probability of sample unit i.
For LPM1, LPM2 and SCPS the Horvitz-Thompson estimator has been also used with calibrated weights based on the spatial coordinates taken both in linear and quadratic forms. In the linear case, the calibrating variables are the horizontal and vertical coordinates. The quadratic specification considers also the square of the coordinates and their cross product. On the other hand, the spatial coordinates, in the linear and quadratic specifications, are also used as balancing variables for the BS and DBSS designs. All designs have been implemented using the R package “Balanced Sampling” (Grafström, [22] ).
A total of 10,000 samples were selected with each design and the relative root mean square error (rRMSE) was estimated as
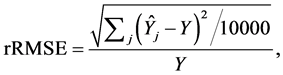
where Y represents the known population total of firm’s sales and 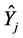 indicates the sample estimate of the j-th sample.
indicates the sample estimate of the j-th sample.
The values of the rRMSE of the different sampling designs have also been compared with the rRMSE’s of the Simple Random Sampling design (SRS) and the Random Pivotal Method design (RPM) in order to better assess the advantage of including space in the sampling procedure. Moreover, it has been computed the following indicator
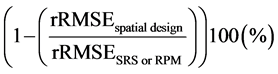
to measure the efficiency gains of spatial designs with respect to SRS or RPM more precisely (see Table 1 and Table 2).
The general indication from Table 1 and Table 2 is that rRMSE’s of spatial designs are lesser than those of non-spatial designs.
In the context of equal inclusion probabilities, DBSS proved to be the most efficient design. Good results are also obtained by LPM1, LPM2 and BS, while SCPS has results slightly worse, for all sample sizes. In this context, the calibration of Horvitz-Thompson estimator in quadratic form provided very similar results as those obtained without any calibration or with the linear calibration on the coordinates. Furthermore, balancing on quadratic spatial coordinates has resulted in a high loss in terms of efficiency of sample estimates.
In the unequal inclusion probability scenario, results are markedly different. Firstly, the efficiency gain of spatial designs with respect to RPM design is very high. Secondly, DBSS has been confirmed as the best method for establishment surveys, with the efficiency gain that increase with the increasing of sample size. Thirdly, LPM1, LPM2 and BS are confirmed as efficient methods also in this case. Finally, the performance of SCPS increases greatly. On the other hand, calibrating and balancing on quadratic spatial coordinates do not produce a notable increase in efficiency of estimation.
Since DBSS is a combination of LPM2 and BS, it shows the theory expressed by Grafström and Tillé [5] and by Grafström and Lundström [23] , for which samples well spread in the space are also balanced. This is especially true in the present case, where the “doubly spatial” connotation which has been given to DBSS leads to an increase in efficiency, whether in equal or unequal inclusion probability situations.

Table 1. Relative root mean square error of population and efficiency gain for equal inclusion probabilities.

Table 2. Relative root mean square error of population and efficiency gain for unequal inclusion probabilities.
The behavior of simulations using geographic coordinates in quadratic explanation is ascribable to the specific nature of the present study, where there is not a quadratic relationship between coordinates. Probably in different kinds of studies about firms it is possible to recognize an advantage to consider coordinates in quadratic form.
Concerning the ability of spatial sampling designs to produce well spread samples, the spatial balance has been measured following the Voronoi polygons approach suggested by Steven and Olsen [9] and recalled by Grafström et al. [3] . Supposing that 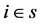 is a sample unit of sample s, the Voronoi polygon is a subarea of the space which includes all population units located closer to i than to any other j-th sample unit. Let
is a sample unit of sample s, the Voronoi polygon is a subarea of the space which includes all population units located closer to i than to any other j-th sample unit. Let 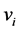 be the sum of the inclusion probabilities of units in the Voronoi polygon of the i-th sample unit, then
be the sum of the inclusion probabilities of units in the Voronoi polygon of the i-th sample unit, then 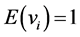 and
and 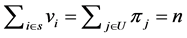 (Grafström et al., [3] , pp. 516-517). To have a spatially balanced sample, all
(Grafström et al., [3] , pp. 516-517). To have a spatially balanced sample, all 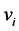 in the sample s must be close to 1, and the variance
in the sample s must be close to 1, and the variance
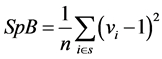
could be used as a measure of spatial balance for the sample s. Therefore, to assess the ability of spatial sampling designs to produce well spread samples, the mean of SpB over the 10,000 drawn samples has been considered (see Table 3). Lower is its value, higher is the degree of spatial balance.
As can be noted from Table 3, in both the contexts of equal and unequal inclusion probabilities, LPM1, LPM2, SCPS and DBSS tend to produce samples that are much more spatially balanced than the non-spatial designs (SRS/RPM). On the other hand, performances of BS in terms of spatial balance are in line with SRS/RPM results, because spatial coordinates have been used in BS only as auxiliary variables and not as spread variables. The results for BS spatial balance could also be explained by the fact that balancing on the geographical coordinates allows only capturing large-scale spatial trend. However, as shown by the empirical semivariogram of Figure 2, the data used in this simulation study are characterized by small-scale spatial autocorrelation that, in contrast, is perfectly captured by LPM1, LPM2, SCPS and DBSS which are the designs that take into account all distances amongst units.
5. Discussion
Spatial sampling designs give a new important point of view to economic analysis. As shown, all spatial designs proposed have a greater efficiency gain with respect to non-spatial designs. In the context of business surveys, results of sampling are strongly related with the peculiarities of the population, wherein it is relevant if there is relevant spatial autocorrelation or not.
Furthermore, a comparison between methods which select samples spread in the space and methods which are balanced on geographic coordinates has been conducted. The result tells that the only method which is spread and balanced in the same time is more efficient, even in the case where the relationship between geographical variables is not linear, i.e. quadratic form. Moreover, if coordinates are used both as spread variables and balancing variables, results are even more fulfilling in terms of efficiency in estimation.

Table 3. Spatial balance of drawn samples.
Future researches in spatial establishment surveys could regard different contexts. It may indeed be possible that in other spatial distributions of establishments with different characteristics, the spatial design shows a different behavior. The availability of more complete information about firms could give an improvement in estimation using spatial sampling designs.
Acknowledgements
The authors are grateful to Anton Grafström (University of Umeå) for his research about spatial sampling which gives the possibility to make progress in economic spatial sampling. They are also grateful to Prof. Yves Tillé (Université de Neuchâtel) for his invaluable guidance and support during the preparation of this paper. Last but not least, they express a sincere thanks to Danila Filipponi of the Italian Institute of Statistics (ISTAT) for her help and assistance with the ASIA archive.