Reply to Comment on “On Humbert Matrix Polynomials of Two Variables” ()
Introduction and Motivation
This reply is written as an answer to the paper [2] [3] .
In the comment [2] , the author points out that the generating matrix function given in Formula (7) in our recently published paper [1]
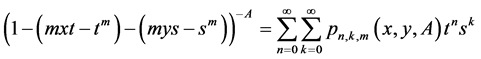
is not true, because the domain is not clarified. And the author notes, that 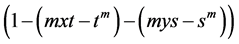
for that it can be zero, and then it is meaningless. Further he writes: “For this, first we have to observe that for matrix , we define
, we define 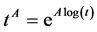 where
where  is the exponential matrix. Of course,
is the exponential matrix. Of course,  has sense only for
has sense only for ”. To clarify the situation, let us write down the relation for any matrix
”. To clarify the situation, let us write down the relation for any matrix  in
in  the following relation
the following relation
 (1)
(1)
holds [4] (see also [5] [6] ). From above we maintain that , from above and from (1) we conclude our reply by noting that the relation ( Humbert matrix polynomials of two variables (7) [1] ) is generated by
, from above and from (1) we conclude our reply by noting that the relation ( Humbert matrix polynomials of two variables (7) [1] ) is generated by
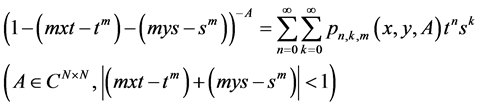
where  is positive integer.
is positive integer.
In paper [3] the author notes that in “Remark” comments that the double generating Formula (8) [7]
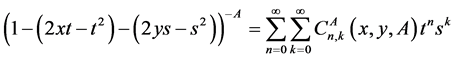
is not true. We conclude our reply by noting that we consider our relation (8) with the help of (1) provided that
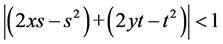 and not equal 1. Note that, in a variety of different research papers our own paper it has been written with approximate resemblance with other papers in the methods, for example, Dattoli et al. [8] and Pathan and Khan [9] . In conclusion, we accept blame for not clarifying the domain because this perhaps causes misunderstanding for readers who are not totally familiar with literature in this area. However, note that even accepting Soler interpretation, from (1) which is written in [1] [7] and it is not mentioned in Soler comments [2] [3] , the conjecture counter examples remain false in [2] [3] . However, our results are original and correct.
and not equal 1. Note that, in a variety of different research papers our own paper it has been written with approximate resemblance with other papers in the methods, for example, Dattoli et al. [8] and Pathan and Khan [9] . In conclusion, we accept blame for not clarifying the domain because this perhaps causes misunderstanding for readers who are not totally familiar with literature in this area. However, note that even accepting Soler interpretation, from (1) which is written in [1] [7] and it is not mentioned in Soler comments [2] [3] , the conjecture counter examples remain false in [2] [3] . However, our results are original and correct.
AMS 2010 Subject Classification
Primary 33C45, 15A15. Secondary 33C45, 15A60