Baryon Magnetic Moment in the Scalar Strong Interaction Hadron Theory ()
1. Introduction
The existing treatments of baryon magnetic moment are all phenomenological and based upon models [1] . The predicted results depend upon free parameters introduced and lack theoretical foundation, unlike the derivation of electron’s magnetic and anomalous magnetic moments from the established Dirac equation and QED. Here, the main stream first principle’s theory, Quantum Chromodynamics [2] , cannot be applied to this problem; it does not work at low energies. Therefore, the scalar strong interaction hadron theory, a first principle’s theory which has proven to be rather successful in accounting for low energy, so far mainly mesonic phenomena, has been applied to this problem
2. Baryon Wave Equations in Electromagnetic Field
The baryon magnetic moment has been treated [3] using a first principle’s theory, the scalar strong interaction hadron theory [4] . In [3] , however, the quark coordinates in the electromagnetic potential were approximated by those of the baryon. The quarks were also assumed to be static. The results of [3] are about 1/3 of the measured ones [2] .
These two approximations are removed here and the factor 1/3 drops out; the results are now in approximate agreement with data. This paper is thus nearly the same as the 1994 paper [3] without these two approximations and relies on the book [4] . The total equations of motion for the octet baryons ([4] (9.3.9)) have been generalaized to include U(1) gauge fields A to become [3] (5.1),
(1a)
(1b)
Here, I, II and III refer to the three quarks, x stands for the 4 vector xm, c and y the baryon wave functions in space time where the undotted and dotted spinor indices run from 1 to 2, Fb the interquark scalar strong interacton ([4] (9.2.11)) producing confinememt, and analogous to [4] (3.1.4).
(2)
The d function is not a Lorentz invariant. Further, z, u, and v stand for the internal coordinates zI, zII and zIII, respectively, x the internal baryon function, p, s, q the flavors of the three quarks, m3op the quark mass operator ([4] (9.3.8, 12, 13)), and qop the quarks charge operator ([3] (2.8)), ([4] (2.3.14)),
(3)
3. Internal Baryon Wave Functions
The normalized internal functions for the octet baryons reads ([3] (8.1)),
(4)
In passing, it is pointed out that these internal functions [5] are essential to the present theory. By exploiting a symmetry among z, v and u, the QCD Lagrangian [2] has been derived from this theory [4] in the high energy limit [6] . These x’s can be removed by multiplying (1) by xpsq = (xpsq)* via [3] (2.5a),
(5)
These q’s are given on lines 2 and 3 of Table 1 below.
Gauge invariance of (1) is shown in the same way as that for mesons in ([4] (6.3.1, 2)) extended to include a third quark. The external electromagnetic field is static and has no time component,
(6)
Table 1. Octet baryon magnetic moments from (17) using the q’s from (5). There are no data for S0, only the transition magnetic moment S0 ® L.
4. Transformation into Laboratory and Relative Coordinates
Taking the left operator of (1b) and operating it on (1a) and making use of (1b, 3-6) leads to [3] (5.4),
(7)
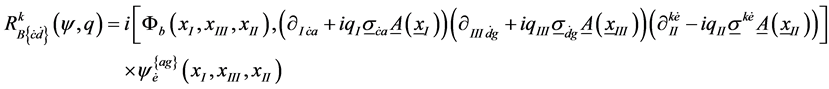(8)
where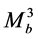 
is the eigenvalue of m3op ([4] (9.3.15, 17, 19)), [A, B]=AB-BA. A sister pair of equations are obtained for y and RB(c,q) by reversing the roles of (1a) and (1b). Note that the three braced operators refer to different coordinates and therefore commute with each other.
Following [3] (6.1, 4), let
(9a)
so that by relations of the type of (2),
(9b)
The relative energies in [3] (6.4) has been put to 0 in accordance with [4] (3.5.6). Alternatively, [4] (3.1.10a) type of relations can be used to remove them to arrive at [4] (10.1.2). Here X is the laboratory coordinate of the baryon and x and y are the relative coordinates of the quarks shown in Figure 1(a).
5. First Order Relations and Magnetic Moment
In the the absence of electromagnetic perturbation or putting the A´s to zero, (1) reduces to the zeroth order equations ([4] (9.3.9)). A in (7, 8) will now produce a pertubation of c and y in (7) so that, in terms of (9),
(a) (b) (c)
Figure 1. (a) illustrates the general (9a), (b) the zeroth order quark-diquark configuration with xI = xIII = xI,III, d = 1/2 in (9a), ([4] (10.1.1)), X0 denotes the zeroth order laboratory coordinates, (c) special case of (a) with c = 1/2 and d = 1/3, giving a maximally allowed E1b in (16).
(10)
where the subscript 1 denotes first order pertubation, E0 denotes the baryon mass and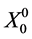 
is that in Figure 1(b), as does x in c which enters the zeroth order ([4] (10.1.2)). The first line beneath (9b) is noted.
Let the external magnetic field be
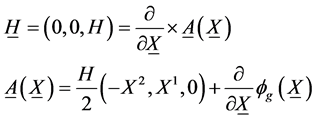(11)
where jg(X) is a gauge functon. With (9), we find
(12)
The apparoximation made beneath (4.1) in [3] keeps only the first term on the right of (12). This turns out to be the reason that the results in (7.10) and Table 1 there are three times too small.
After inserting (10) into (7), we wish to obtain the perturbed baryon energy E1b as a function of the first order q´s there. With (2), (9), (11), and Figure 1(a), the first order part of the first braces in (7) reads
(13)
The zeroth order part of the remaining two braces in (7) is found from (9) and Figure 1(b) and is
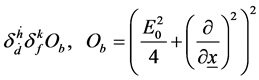(14)
The first order parts of the second and third braces in (7) are analogously found; the associated zeroth order parts are of the same form as the last of (14). The first order part of (7) now reads
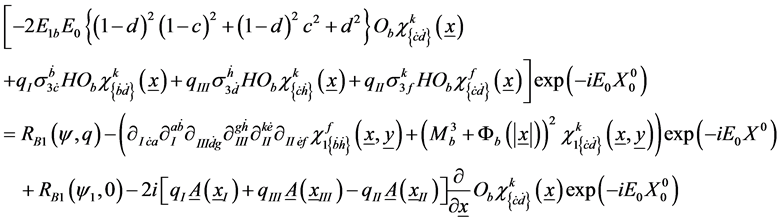(15)
Here, it has been noted that Figure 1(a) and Figure 1(b) show that 
and X0 differ by a quantity independent of each of them so that
. Note that the strong interaction Fb for a free baryon and m3op are not affected by the perturbative A fields and operate only on zeroth order wave functions. The argument of c and Fb has thus been changed to reflect that Figure 1(b) applies. RB1 denotes the first order part of (8).
The dominating contributions to the energy shift E1b in the first term of (15) comes from the three qs3 terms on the left of (15) which contribute equally, but of opposite signs, to E1b for spin up and spin down wave function components shown in (16b) below. The second and third terms on the right of (15) are just the zeroth order part of (7, 8) and can be absorbed into it. The first and last terms on the right of (15) do not contain s3 splitting term and their contributions to E1b are of the same sign for the spin up and down components. These contributions, to the degree that they are of equal magnitude, cancel out in the evaluation of the magnetic moment. These two terms will be ignored here to arrive at an approximate expression of the magnetic moment.
The zeroth order c on the remaining left of (15) for the spinor index c = 1, 2 are eigenfunctions of the qs3 operators; we obatin the equivalent of [3] (7.3),
(16a)
(16b)
The doublet wave functions ([3] (7.4)] are reproduced in (16b) and are the spin up m = 1/2 part ([4] (10.3.8a)). The corresponding spin down m = -1/2 part ([4] (10.3.8b)) is basically (16b) with the both expressions interchanged. The radial wave functions g0(r) and f0(r) have been plotted in ([4] Figure 11.1).
The space dependent part associated with Ob in (16a) drops out, just like that in [3] (4.5b) or [4] (6.3.12) for vector meson. The maximally allowed stationary energy shift E1b is found for c = 1/2 and d = 1/3, same as [3] (7.9). Let Ep be the proton massn magnetic moment reads
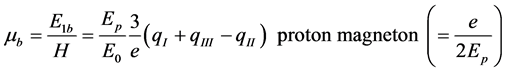(17)
which is 3 times the 1994 result ([3] (7.10)) without neglect of quark motion beneath (8.3) there. The results are shown on line 4 in Table 1 and are in approximate agreement with data [2] on line 5.
6. Conclusion
The baryon magnetic moment has been treated for the first time starting from a first principle’s theory, the scalar strong interaction hadron theory, that the predicted results are in approximate agreement with data which lends further support to the fact that this theory is basically viable and can replace QCD at low energies.
It is conjectured that the difference between the last two lines in Table 1 may be due to the first term RB1 on the right of (15). This “rest” term arises from the strong quark-diquark interaction F(r); its effect resembles spin-orbit coupling in atomic physics. Its inclusion calls for numerical integration. The last term of (15) can be balanced off by including the equally probable spin down m = -1/2 wave functions of [4] (10.3.8b) mentioned beneath (16b). An additional degree of freedom is the choice of the gauge function jg(X) in (11); the simplest form is a constant which does not contribute to (11).